U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| TECHBRIEF |
| This techbrief is an archived publication and may contain dated technical, contact, and link information |
| Publication Number: FHWA-HRT-12-032 Date: July 2012 |
Publication Number: FHWA-HRT-12-032 Date: July 2012 |
PDF files can be viewed with the Acrobat® Reader®
FHWA Contact: Larry Wiser, HRDI-30, (202) 493-3079, larry.wiser@dot.gov
This document is a technical summary of the Federal Highway Administration report, Estimation of Key PCC, Base, Subbase, and Pavement Engineering Properties from Routine Tests and Physical Characteristics (FHWA-HRT-12-030).(1)
This TechBrief presents models developed by statistical methods to predict key material properties for portland cement concrete (PCC), chemically stabilized materials, and unbound base, subbase, and subgrade materials. It also presents models to predict design inputs specific to the Mechanistic-Empirical Pavement Design Guide (MEPDG).(2) The models were developed under the Long-Term Pavement Performance (LTPP) data analysis study, Estimation of Key PCC, Base, Subbase, and Pavement Engineering Properties from Routine Tests and Physical Characteristics.(1) The predictive models were developed using data from the LTPP database as well as data generated from analyses used in the calibration of the MEPDG distress models under National Cooperative Highway Research Program Project 1-40D.(3 4)
Material characterization is a critical component in all aspects of pavement engineering—analysis, design, construction, quality control (QC) and quality assurance (QA), pavement management (PM), and rehabilitation. At each stage during the life of a project, the influence of fundamental engineering material parameters on the long-term performance of the pavement can be predicted using advanced tools like the MEPDG.(2) Measuring the properties directly is preferable, but it is often not practical or possible. Consequently, there is a need for reliable models that can be used to estimate key parameters and provide more information about material properties, which is addressed to only a limited extent with currently available laboratory and field testing resources.
Reliable correlations between material properties and a combination of mix design parameters, physical characteristics, and index properties offer a cost-effective alternative and are equivalent to the level 2 inputs used in the MEPDG. The LTPP database offers an opportunity to develop correlation equations to estimate material properties.(3) Therefore, it served as the primary source of data in developing the models presented here. To develop models for design feature parameters specific to the MEPDG, LTPP data were combined with data generated from MEPDG analyses of LTPP sections.
In selecting key material properties that required predictive models, the following parameters were considered:
Predictive models were developed for PCC compressive strength, PCC flexural strength, PCC elastic modulus, PCC tensile strength, lean concrete base modulus, and unbound materials resilient modulus. In addition, rigid pavement design feature input properties were developed using the MEPDG calibration data. These include the jointed plain concrete pavement (JPCP) and the continuously reinforced concrete pavement (CRCP) deltaT parameter, which is defined as the equivalent temperature differential that corresponds to the effective permanent curl-warp locked into the pavement. For all PCC material properties, multiple models were developed for use under different project situations.
In developing the models, a uniform set of statistical criteria were used to select independent parameters to define a relationship as well as to mathematically formulate prediction functions. The analyses examined several statistical parameters in choosing the optimal model and determining the predictive ability of the model. In general, the optimal set of independent variables (Mallows coefficient, Cp), the interaction effects (variance inflation factor), the significance of the variable (p-value), and the goodness of fit (R2) were verified. Additionally, the study validated and/or refined existing models and developed new relationships. In the statistical analyses, the following tasks were accomplished:
This section provides a summary of the models. Refer to the corresponding main report, Estimation of Key PCC, Base, Subbase, and Pavement Engineering Properties from Routine Tests and Physical Characteristics, for detailed information about the quality of the predictive models and the range of data that can be applied to each model.(1) Figure 1 through figure 5 present the PCC compressive strength models, figure 6 through figure 8 present PCC flexural strength models, figure 9 through figure 11 present PCC elastic modulus models, figure 12 presents a PCC indirect tensile strength model, and figure 13 and figure 14 present PCC CTE models. Note that the elastic modulus models yielded a correlation with a low R2 and need to be used with caution.
The applications for figure 1 are 28-day strength for design and QA.
![]()
Figure 1 . Equation. Compressive strength model 1 for 28-day cylinder strength.
The applications for figure 2 are design, QA, PM, and opening strength for ages less than 1 year.
![]()
Figure 2. Equation. Compressive strength model 2 for short-term cylinder strength.
The applications for figure 3 are design, QA, PM, and opening/in situ strength for ages less than 1 year.
![]()
Figure 3. Equation. Compressive strength model 3 for short-term core strength.
The applications for figure 4 are design, QA, PM, and in situ strength at any age.
![]()
Figure 4. Equation. Compressive strength model 4 for all ages core strength.
The applications for figure 5 are rehabilitation design and in situ strength for ages greater than 5 years.
![]()
Figure 5. Equation. Compressive strength model 5 for long-term core strength.
Where:
fc,28d = Compressive strength at 28 days.
fc,t = Compressive strength at time t, days.
fc,LT = Long-term compressive strength.
w/c = Water/cementitious materials ratio.
CMC = Cementitious materials content, lb/ft3.
uw =Unit weight, lb/ft3.
t = Age, years.
MAS = Maximum aggregate size, inch.
FM = Fineness modulus of fine aggregate.
The applications for figure 6 are design and PM when compressive strength at a given age is available.
![]()
Figure 6. Equation. Flexural strength model 1 based on compressive strength.
The applications for figure 7 are design and PM when index properties are available and predicting for any age.
![]()
Figure 7. Equation. Flexural strength model 2 based on age, unit weight, and w/c ratio.
The applications for figure 8 are design and PM when index properties are available and predicting for any age.
![]()
Figure 8. Equation. Flexural strength model 3 based on age, unit weight, and CMC.
Where:
MR = Flexural strength, psi.
MRt = Flexural strength at age t years, psi.
f'c = Compressive strength determined at the same age, psi.
w/c = Water/cementitious materials ratio.
CMC = Cementitious materials content, lb/yd3.
uw = Unit weight, lb/ft3.
t = Pavement age, years.
The applications for figure 9 are design and PM when compressive strength at given age and aggregate type are available.
![]()
Figure 9. Equation. Elastic modulus model 1 based on aggregate type.
The applications for figure 10 are design and PM when compressive strength at a given age is available (predicts for any age).
![]()
Figure 10. Equation. Elastic modulus model 2 based on age and compressive strength.
The applications for figure 11 are design and PM when 28-day compressive strength is available (predicts for any age).
![]()
Figure 11. Equation. Elastic modulus model 3 based on age and 28-day compressive strength.
Where:
Ec =PCC elastic modulus, psi.
Et = Elastic modulus at age t years.
Ec,t = Elastic modulus at age t years.
f’ct = Compressive strength at age t years.
uw = Unit weight, lb/ft3.
f’c = Compressive strength at same age, psi.
f’c, 28-day = 28-day compressive strength.
t = Age at which modulus is determined, years.
Dagg = Regressed constant depending on aggregate type: andesite (1), basalt (0.9286), chert (1.0079), diabase (0.9215), dolomite (1.0254), granite (0.8333), limestone (1), quartzite (0.9511), and sandstone (1).
The application for figure 12 is design when compressive strength is available.
![]()
Figure 12. Equation. PCC indirect tensile strength model based on compressive strength.
Where:
ft = Indirect tensile strength of the PCC material.
f’c= Compressive strength of the mix determined at the same age.
The applications for figure 13 are design, QC, and PM when coarse aggregate rock type is available.
![]()
Figure 13. Equation. CTE model 1 based on aggregate type.
The applications for figure 14 are design, QC, and PM when coarse aggregate rock type and mix design proportioning are available.
![]()
Figure 14. Equation. CTE model 2 based on mix volumetrics.
Where:
CTEPCC = CTE of the PCC material, x10-6 inch/inch/°F.
VCA = Volumetric proportion of the coarse aggregate (0 to 0.6).
CTECA = Constant determined for each aggregate type (basalt (3), chert (6.4), diabase (3.4835), dolomite (5.1184), gabbro (3.75), granite (4.7423), limestone (3.2886), quartzite (6.1), andesite (3.6243), and sandstone (4.5)).
Figure 15 lists the deltaT model for JPCP for rigid pavements. Because of the limitations of the model developed for CRCP deltaT, this model is not included in this document. The applications are design and PM when mix design and construction weather information are available.
![]()
Figure 15 . Equation. deltaT JPCP design.
Where:
deltaT/inch = Predicted gradient in JPCP slab, °F/inch.
TR = Difference between maximum and minimum temperature in construction month, °F.
SW = Slab width, ft.
PCCTHK = JPCP slab thickness, inch.
uw = Unit weight of PCC used in JPCP slab, lb/ft3.
w/c = Water/cementitious materials ratio.
latitude = Latitude of the project location, degrees.
Figure 16 shows the lean concrete base elastic modulus model. The applications are design and PM when 28-day compressive strength information is available.
![]()
Figure 16 . Equation. Lean concrete base elastic modulus model.
Where:
ELCB = Elastic modulus of the lean concrete base layer.
f’c, 28d = 28-day compressive strength of the lean concrete base material.
Figure 17 shows the model developed for resilient modulus for coarse- and fine-grained base layers and soil. The applications are design, QA, and PM when gradation, Atterberg limits, and moisture content are known.
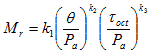
Figure 17 . Equation. Resilient modulus for coarse- and fine-grained base layers and soils.
The parameters in figure 17 are defined in figure 18 through figure 20 as follows where:
Mr = Resilient modulus, psi.
θ = Bulk stress (σ1 + σ2 + σ3).
σ1 = Major principal stress.
σ2 = Intermediate principal stress = σ3 for Mr test on cylindrical specimen.
σ3 = Minor principal stress/confining pressure.
| toct = Octahedral shear stress = |
|
Pa = Normalizing stress (atmospheric pressure).
k1, k2, and k3 = Regression constants (obtained by fitting Mr test data to this model form.
![]()
Figure 18. Equation. Prediction model for k1.
![]()
Figure 19. Equation. Prediction model for k2.
![]()
Figure 20. Equation. Prediction model for k3.
Where:
PCTHALF = Percent passing the ½-inch sieve.
LL = Liquid limit, percent.
OPTMOIST = Optimum moisture content, percent.
PCTNO80 = Percent passing No. 80 sieve.
PCTGRVL = Percent gravel fraction (0.078- to 2.36-inch size).
D10 = Maximum particle size of the smallest 10 percent of soil sample.
Material characterization is critical to pavement analysis, design, and performance prediction. While the availability of the MEPDG has allowed great flexibility in the evaluation of as-designed and as-built pavements, the need for extensive input data can be a challenge for agencies adopting the MEPDG. The ability to develop prediction models for material properties and design features was explored under this study. It was found that information on mix constituents, their physical characteristics, and index properties could be used to develop correlations to predict material properties for PCC materials, stabilized materials, and unbound bases and subgrade materials.
|
Researchers—This study was performed by Applied Research Associates, Inc., Champaign, IL. Distribution—This TechBrief is being distributed according to a standard distribution. Direct distribution is being made to the Divisions and Resource Center. Availability—The report may be obtained from the FHWA Product Distribution Center by email to report.center@dot.gov, fax to (814) 239-2156, phone to (814) 239-1160, or online at https://www.fhwa.dot.gov/research. Key Words—LTPP, Material properties, MEPDG, Prediction model, Index properties, PCC, Compressive strength, Flexural strength, Elastic modulus, Tensile strength, Coefficient of thermal expansion (CTE), JPCP built-in gradient, Lean concrete base, Resilient modulus. Notice—This document is disseminated under the sponsorship of the U.S. Department of Transportation in the interest of information exchange. The U.S. Government assumes no liability for the use of the information contained in this document. The U.S. Government does not endorse products or manufacturers. Trademarks or manufacturers’ names appear in this report only because they are considered essential to the objective of the document. Quality Assurance Statement—The Federal Highway Administration (FHWA) provides high-quality information to serve Government, industry, and the public in a manner that promotes public understanding. Standards and policies are used to ensure and maximize the quality, objectivity, utility, and integrity of its information. FHWA periodically reviews quality issues and adjusts its programs and processes to ensure continuous quality improvement. |