APPENDIX B. MOISTURE DIFFUSION INTO A CYLINDRICAL FRP COMPOSITE

The procedure for calculating moisture diffusion into the FRP of a composite pile is presented in this appendix. The diffusion is assumed to be Fickian, and based on the geometry of the FRP pile, it is further assumed to be predominantly in the radial direction. For these conditions, the governing partial differential equation for the moisture concentration is given by

(70)

where C is the moisture concentration (also C = M(t)) and D_r is the diffusivity for radial diffusion.

If we assume the FRP shell is initially dry, the initial condition for the moisture concentration is given by

(71)

The last requirement for the solution of the diffusion problem is that of the boundary conditions on the inner and outer radii of the FRP shell. As a first approximation, we specify that these concentrations are constant; that is,

(72)

where r_i and r_o are the inner and outer radii, respectively, and C_i and C_o are the corresponding concentrations.

To solve equation 70 subject to the initial condition given by equation 71 and the boundary conditions in equation 72, the separation-of-variables technique can be used. This technique requires homogeneous boundary conditions rather than inhomogeneous conditions. Therefore, a solution of the following form is sought:

(73)

where --satisfies the time-independent form as follows:

(74)

with boundary conditions given by

(75)

This solution is given by

(76)

By combining equation 76 with equations 70 through 72, we find that c(r.t) is the solution of equation 70 with boundary conditions given by

(77)

and an initial condition given by

(78)

Problems of this type have been studied in detail by a number of researchers. In particular, using the results of Necati Ozisik (1989), the solution is given by

(79)

where

(80)

and ß_m represents the positive root of the transcendental

(81)

where J₀ and Y₀ are Bessel functions of the first and second kind (order zero), respectively.

The moisture content for the FRP shell can be bound by two extreme cases that should bound the FRP moisture absorption behavior. In the first case, we assume that the composite is saturated on the outer radius due to its immersion in water, and that it remains completely moisture-free on the inner surface. The corresponding boundary conditions are given by

(82)

where M₈ is the saturation concentration from the experimental data in chapter 4. Assuming that C(r_i,t) = 0 should give the lowest values for the moisture content in the pile, and hence the highest FRP strength (since the strength is reduced by an increase of moisture).

In the second case, we assume that the FRP shell is saturated on both the inner and outer radii. The corresponding boundary conditions are given by

(83)

This case should give us the highest values for the moisture content in the FRP shell of the pile, and hence the lowest FRP strength.

The procedure described above provides a means to estimate the bounds for the moisture content distribution within the FRP shell of a composite pile. To do so, the values of M₈ and diffusivity (D_r) must be known. For the piles studied in this project, these values can be taken from tables 23-26.

The results of this approach for the Lancaster 24-inch FRP shell are shown in figures 235 and 236. These figures correspond to the predicted moisture concentration profiles for the two boundary condition cases described above. The value of D used corresponds to 22 ^oC (72 °F) temperature.

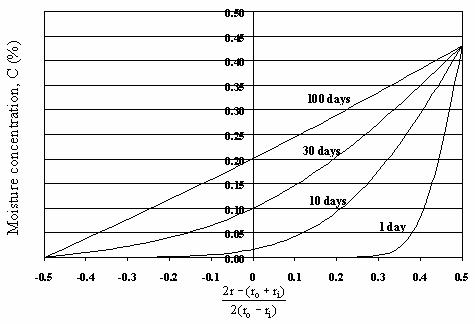
Figure 235. Graph. FRP moisture concentration profile, inner radius dry, outer radius saturated.

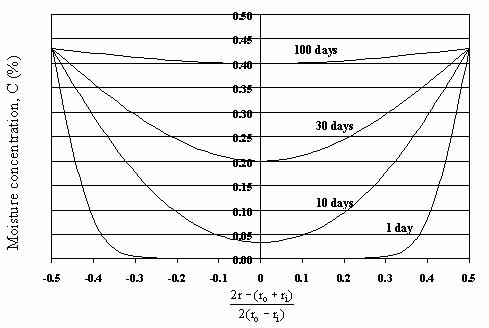
Figure 236. Graph. FRP moisture concentration profile, inner and outer radii saturated.