CHAPTER 4. ANALYTICAL STUDY OF MAXIMUM SCOUR DEPTH
The experiments were conducted under two critical velocity conditions, but the purpose of the experiments was to make the results as widely applicable as possible. To achieve this end, an analytical solution for the maximum scour depth needed to be found.
For clarification, the problem is stated as follows:
Given a bridge over a steady river flow with clear water without contraction channel and piers (shown in plan view in figure 37) experiencing the flow conditions in either figure 38 through figure 40), find the equilibrium maximum pressure flow scour depth, ys, per unit of river flow.
Where:
Vuc = Upstream critical velocity.
B = Width of the river.
W = Width of the bridge deck.
d50 = Median diameter of the bed materials.
hu = Depth of the headwater.
hb = Bridge opening before scour.
hd = Depth of the tailwater.
b = Thickness of the bridge deck including girders.
FLOW CLASSIFICATION
The solution to the problem depends on the tailwater surface elevation. As in Picek et al., the bridge flows are divided into three cases.(6)
Case 1
If the downstream low chord of a bridge is unsubmerged as shown in figure 38, the bridge operates as an inlet control sluice gate. The scour is independent of the bridge width and continues until a uniform flow and a critical bed shear stress are reached. This case occurs only for upstream slightly submerged conditions. Since the flow condition under the bridge in
this case is an open channel flow, it is presented in appendix A.
Case 2
If the downstream low chord is partially submerged as shown in figure 39, the bridge operates as an outlet control orifice, and the bridge flow is rapidly varied pressure flow.
Case 3
If the bridge is totally submerged as shown in figure 40, it operates as a combination of an orifice and a weir. Only the discharge through the bridge affects scour depth. In the following sections, only the solutions for cases 2 and 3 are discussed.
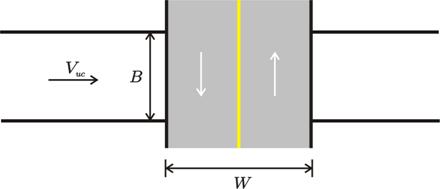
Figure 37. Illustration. Plan view of bridge over stream.
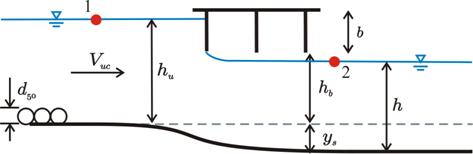
Figure 38. Illustration. Pressure flow for case 1.
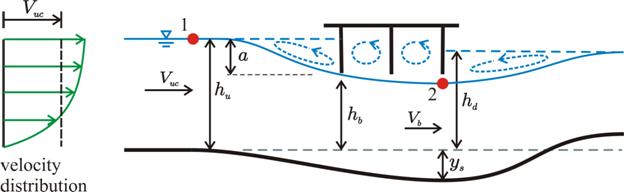
Figure 39. Illustration. Pressure flow for case 2.
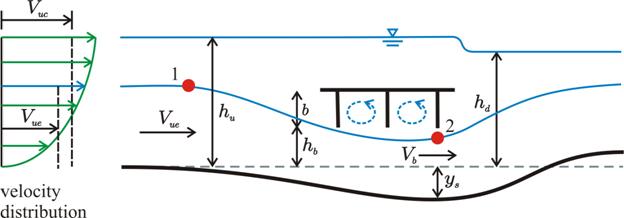
Figure 40. Illustration. Pressure flow for case 3.
CASE 2-PARTIALLY SUBMERGED FLOWS
Neglecting the friction, the energy equation along the streamline 1-2 is shown in the following equation in figure 41:
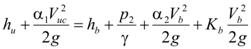
Figure 41. Equation. Energy equation along streamline 1-2.
Where:
α1 and α2 = The energy correction factors.
Kb = The bridge energy loss coefficient which varies with bridge inundation.
The friction loss has been neglected due to the short distance between points 1 and 2.
The pressure at point 1, p1, represents atmospheric pressure. It is assumed that p1 = zero, so it is eliminated from the energy equation. The pressure at point 2, p2, under the bridge is not hydrostatic and therefore must be solved from the Bernoulli equation applied across streamlines.(9) Referring to figure 94 in appendix B, figure 42 is generated.
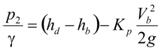
Figure 42. Equation. Pressure under the bridge, p2.
Where:
hd = The depth of the tailwater.
Kp = A curvature coefficient that, like Kb, varies with bridge inundation.
The difference term in parentheses in figure 42 is the hydrostatic pressure head, while the last term is a curvature pressure head. Substituting the equation in figure 42 into figure 41 gives the following equation in figure 43:
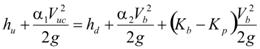
Figure 43. Equation. Energy equation including curvature coefficient.
Since both Kb and Kp are related to bridge inundation and must be zero when hu = hb corresponds to open channel flow, the following equation in figure 44 is assumed:
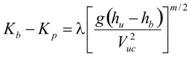
Figure 44. Equation. Model describing difference bridge energy loss coefficient and curvature coefficient.
In figure 44,λ and m are determined experimentally. The gravitational acceleration, g, and Vuc are involved because of dimensional homogeneity. Substituting figure 44 into figure 43 and rearranging it gives the following equation in figure 45:
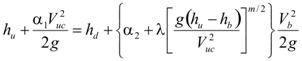
Figure 45. Equation. Energy equation including empirical parameters.
Figure 45 can be rearranged, as in the following equation in figure 46:
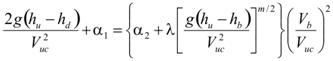
Figure 46. Equation. Rearrangement of energy equation including empirical parameters.
Considering the continuity in figure 47, as follows:
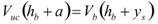
Figure 47. Equation. Continuity equation.
Where:
a = hu- hb, as shown in figure 39.
The equation in figure 46 becomes figure 48, where the left side of the equation, (hb+ys)/(hb+a), is called the scour number.

Figure 48. Equation. Pressure flow scour design equation.
Unfortunately, the downstream flow depth, hd, is unknown. For approximation, figure 49 is assumed to be a function defined as follows:
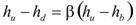
Figure 49. Equation. Downstream flow depth approximation.
Where zero <β < 1. Concisely, F is defined in figure 50 as follows:
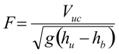
Figure 50. Equation. Inundation Froude number.
Figure 50, when combined with the equations in figure 49 and figure 48, is reduced to the following equation in figure 51:
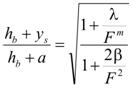
Figure 51. Equation. Pressure flow scour design equation including inundation Froude number.
The values of α1 and α2have been taken as 1, and the parameters λ, m, and β are determined experimentally. The equation in figure 51 will be tested after case 3 is discussed.
CASE 3-TOTALLY SUBMERGED FLOW
The solution for case 2 can be adapted to case 3 after a slight modification. This can be proven by applying the energy equation (figure 41) to the situation in figure 40. The effective velocity, Vue, at point 1 is significantly affected by the bridge deck. As an approximation, the relation in the following equation in figure 52 is assumed:
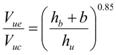
Figure 52. Equation. Effective velocity equation.
The exponent 0.85 is a fitting constant derived from the data in the graph shown in figure 53.
 |
| 1 mm = 0.039 inches |
Figure 53. Graph. Scour number versus inundation Froude number.
The unit discharge, q1, through the bridge is then described in figure 54 as follows:
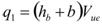
Figure 54. Equation. Unit discharge.
The velocity at the maximum scour section is illustrated in the equation in figure 55 as follows:
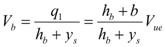
Figure 55. Equation. Velocity at maximum scour section.
When the equation in figure 41 is applied to the situation in figure 40, the pressure at point 1, p1, is
hydrostatic, and the pressure at point 2, p2, is the same as that in figure 42. Substituting the equation in figure 55 into figure 46 and rearranging it gives the following equation in figure 56:

Figure 56. Equation. Pressure flow scour design equation including effective velocity.
Figure 56 is the same as figure 48 except the deck block depth, a, is replaced with the deck thickness, b, and the upstream critical velocity, Vuc, is replaced with the effective velocity, Vue. In general, cases 2 and 3 can be unified with the equation in figure 51 where the conditions in the equations in figure 57 through figure 59 are applied.
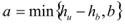
Figure 57. Equation. Deck block depth for cases 2 and 3.
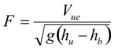
Figure 58. Equation. Inundation Froude number for cases 2 and 3.
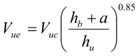
Figure 59. Equation. Effective velocity for cases 2 and 3.
Note that for case 2, the effective velocity, Vue, reduces to the critical velocity, Vuc.
MAXIMUM SCOUR DEPTH
Test of the Hypothesis
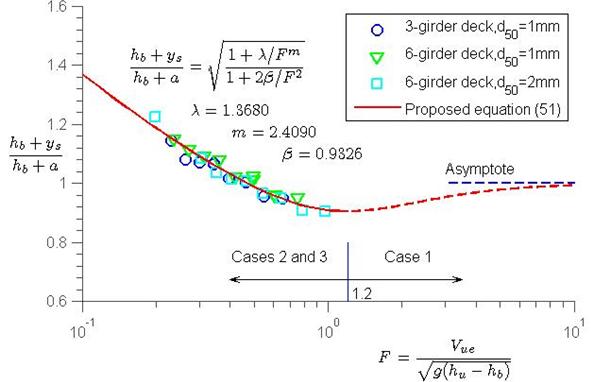
It is hypothesized that the maximum scour depth for cases 2 and 3 can be described in figure 51 where λ and m are positive and zero < β < 1. To test the equation in figure 51, the inundation Froude number, F, and the scour number, (hb+ys)/(hb+a), for the experimental data are listed in table 1 through table 3 in columns 4 and 5, respectively, which are also plotted in figure 53. Applying the data to the equation in figure 51 and using the least-squares fitting function in MatLab®, the model parameters are obtained as follows:
Where:
λ = 1.3680.
m = 2.4090.
β = 0.9325.
The correlation coefficient R2 = 0.9639.
Figure 53 shows that F and the scour number are appropriate similarity numbers to describe bridge pressure flow scour since all the data fall into a single curve regardless of bridge girder and sediment size. In addition, the curve has a minimum value at F = 1.2 and (hb+ys)/(hb+a)
= 0.9055, corresponding to the criterion between cases 1 and 2. The figure also shows that the proposed equation agrees well with the data when 0.2 ≤ F ≤ 1, which corresponds to 1.14 ≤ hu/hb ≤ 3.57. Finally, the dashed line for case 1 is an extension of figure 51. Mathematically, when hu approaches hb, F approaches infinity, and the scour number has an asymptote, (hb+ys)/(hb+a) → 1, which gives ys → zero, since a → zero. This asymptote shows that the structure of figure 51 is reasonable. In terms of design, case 1 (where F >1.2) is trivial since its scour is less than those of cases 2 and 3.
The Effect of Sediment Size
When sediment size increases, Vuc increases. The increase in Vue can be computed according to the equation in figure 59. F then increases, which results in a decrease in the scour number. As a result, scour depth decreases with increasing sediment size.
The Effect of Deck Inundation
The bridge opening, hb, appears in both axes in figure 53. To study the effect of hb, the equation in figure 51 is rewritten in the equation in figure 60 as follows:
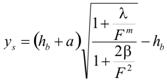
Figure 60. Equation.Maximum scour depth calculation.
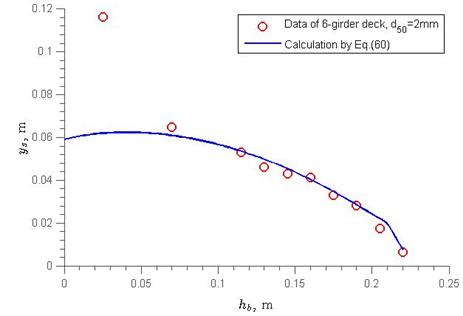
For example, examine the six-girder deck with 0.078 inches (2 mm) of sediment for an experiment. The equation in figure 60 is
plotted along with the measured experimental data in figure 61, which shows that when hb > 0.164 ft (0.05 m), scour depth decreases with increases in the bridge opening hb. However, if hb ≤ 0.164 ft (0.05 m) or the deck is close to the bed, the scour calculation from figure 60 is significantly less than the measured value. This deviation results from the velocity profile near the bed. When the deck is close to the bed, Vue is significantly smaller, and the energy correction factors α1 and α2 are much larger than the assumed value of 1. In other words, the proposed equation in figure 51 is only valid when the bridge deck is a sufficient distance above the bed, such as hb/hu > 0.28.
 |
1 mm = 0.039 inches
1 m = 3.28 ft |
Figure 61. Graph. Maximum scour depth versus bridge opening height.
The Effect of Deck Thickness
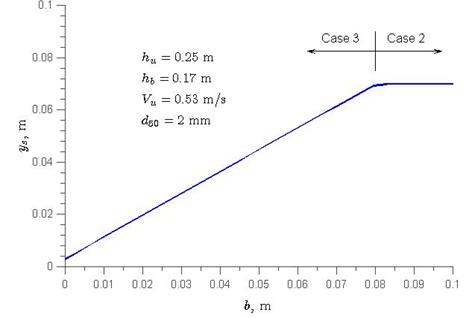
The definition of deck thickness, b, is shown in figure 38 through figure 40. Obviously, for case 2, the scour is independent of deck thickness. Nevertheless, for case 3, the scour varies with deck thickness. Figure 62 shows an example of the ys versus b relationship, assuming that all other variables remain constant. It shows that for case 3, ys increases almost linearly with b. This implies that to reduce ys, b should be minimized in design.
 |
1 mm = 0.039 inches
1 m = 3.28 ft |
Figure 62. Graph. Maximum scour depth versus bridge thickness.
From this chapter, it is concluded that (1) case 2 or 3 occurs when F ≤ 1.2; (2) cases 2 and 3 can be unified by the equation in figure 51 when the conditions in figure 57 through figure 59 are applied; and (3) once the maximum scour depth is estimated using figure 51, the scour profile can be calculated by the equations in figure 22 and figure 23. The next chapter focuses on the application of the results of this study through several examples.
CHAPTER 5. DESIGN PROCEDURE AND APPLICATION EXAMPLES
CRITICAL VELOCITY EQUATION
The design with the equation in figure 51 or figure 53 requires the critical approach velocity. Besides Neill's critical velocity equation and the equation in figure 4, several other velocity equations are available in the literature corresponding to a specific sediment size range. A general equation for the velocity can be derived from the Manning equation and the Shields diagram.(4)
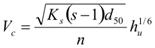
Figure 63. Equation. Critical velocity.
Where:
Ks = The critical Shields number.
The Manning coefficient, n, is calculated via the following equation in figure 64:
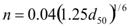
Figure 64. Equation. Manning coefficient.
Substituting figure 64 into figure 63 gives the critical velocity equation in figure 65 as follows:
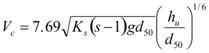
Figure 65. Equation. Critical velocity.
In the equation in figure 65, the gravitational acceleration, g, is considered for dimensional homogeneity, and Ks can be approximated by figure 80 in appendix A.
Figure 4 is a special case of figure 65 where Ks = 0.039, corresponding to a sand diameter d50 = 0.0585 inches (1.5 mm). The equation in figure 65 is a general critical velocity equation for sands based on the Shields diagram, and it is recommended in this report.
Design Procedure
Consider the design procedure for the following problem:
Given a design unit discharge q, bridge opening hb, deck thickness b, and bed material diameter d50, find the scour depth, ys, and scour profile.
The design procedure exists as follows:
-
Use the Hydrologic Engineering Centers River Analysis System (HEC-RAS) program to estimate the approach flow depth hu. Note that the proposed method is based on rectangular flume experiments. For natural channels where flow depths are not uniform in the lateral dimension, a representative local depth, hu, should be used.
-
Calculate the critical velocity, Vuc, from figure 65. If the upstream velocity, Vu, is less than or equal to Vuc, the proposed equation in this report is used. Otherwise, a procedure for live bed scour should be used.
- Calculate the deck block depth, a, for clear water scour using the equation in figure 57.
- Calculate the effective upstream velocity, Vue, using the equation in figure 59.
-
Calculate the inundation Froude number, F, using the equation in figure 58 and check if the bridge flow is under pressure flow where F ≤ 1.2.
- Calculate the pressure flow scour depth, ys, using the equation in figure 60.
- Plot the design scour profile according to figure 22 and figure 23.
Column 6 in table 1 through table 3 is obtained using the above procedure. Column 7 shows that except for a few tests with little scour and in instances where the deck was positioned very close to the bed, most of the calculations generated using the equation in figure 51 are within 10 percent of the measured values.
APPLICATION EXAMPLES
Example 1 (Foundation Design)
The following example is modified from HEC-18:(4)
An existing bridge with a deck width of 30.28 ft (10 m) supported by five girders is subjected to pressure flow during a 100-year flood. There is only a small increase in flow depth at the bridge for the 500-year flood due to the large overbank area. The bed materials are characterized by a size of d50 = 0.078 inches (2 mm), and the bridge opening is hb = 26.01 ft (7.93 m) before scour occurs. Assuming that the deck thickness including the girders and guardrail is b = 6.56 ft (2 m) for case 2 and b = 3.28 ft (1 m) for case 3, calculate the maximum vertical
contraction scour depth and scour profile using the previously listed steps.
1. Assume that the HEC-RAS program is used to get the following flow conditions:
hb= 31.98 ft (9.75 m).
Vu= 3.28 ft/s (1.0 m/s).
q = 104.95 ft2/s (9.75 m2/s).
2. Calculate the critical velocity according to figure 65. First, d* and Ks (which are defined in figure 81 and figure 82) are calculated in figure 66.
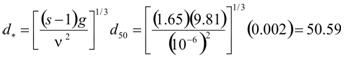
Figure 66. Equation. Dimensionless diameter.
The kinematic viscosity has been taken as ν = 10-6. Ks is then calculated as in figure 67.
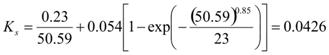
Figure 67. Equation. Critical Shields number.
Vuc is then calculated using figure 68.
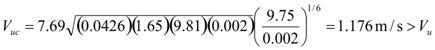 |
| 1 m = 3.28 ft |
Figure 68. Equation. Critical approach velocity.
The results indicate that this is a clear water scour condition. For bridge safety, the critical velocity is applied.
3. Calculate the deck block depth for b = 6.56 ft (2 m), as seen in figure 69.
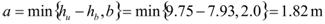 |
| 1 m = 3.28 ft |
Figure 69. Equation. Deck block depth evaluation.
The calculated deck block depth indicates that the flow is of the type represented by case 2. For case 2, the effective upstream velocity is the same as the upstream critical velocity, Vue= 3.86 ft/s (1.176 m/s).
4. Calculate F, as shown in figure 70.
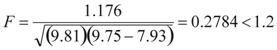
Figure 70. Equation. Inundation Froude number evaluation to determine pressure flow.
The results from figure 70 (i.e. F < 1.2) show the bridge flow is under a pressure flow condition, and
can be described as either case 2 or 3.
Calculating the scour depth using the equation in figure 60, the results are shown in figure 71.
 |
| 1 m = 3.28 ft |
Figure 71. Equation. Scour depth evaluation.
From figure 30, ys is at a distance of x2 from the downstream deck edge. This
distance is solved in figure 72.
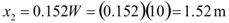 |
| 1 m = 3.28 ft |
Figure 72. Equation. Maximum scour depth position.
5. Estimate the equilibrium scour profile, y, by the equations in figure 22 and figure 23, which is solved in figure 73 for the case when x ≤ zero.
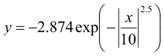
Figure 73. Equation. Equilibrium scour profile equation, x is less than or equal to zero.
6. Calculate figure 74 for x > zero.
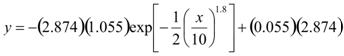
Figure 74. Equation. Equilibrium scour profile equation, x is greater than zero.
7. Simplify figure 74 to generate the equilibrium scour profile in figure 75.
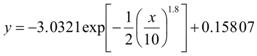
Figure 75. Equation. Simplified equilibrium scour profile equation, x is greater than zero.
The equilibrium scour profile generated by figure 75 is plotted in figure 76.
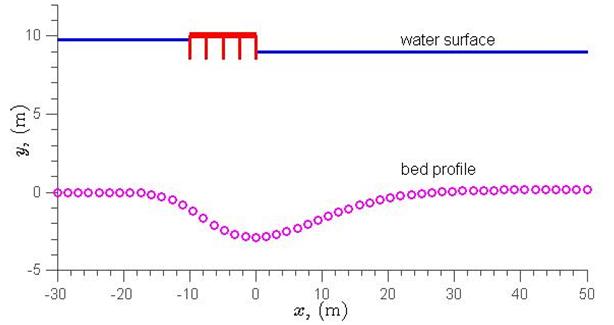 |
| 1 m = 3.28 ft |
Figure 76. Graph. Scour profile for example problem.
Repeating the above steps with b = 3.28 ft (1 m), the maximum scour depth for case 3 can be found. This depth, as calculated by this method, and the other three methods examined previously is shown in the last column of table 4.
The maximum scour depths calculated according to the different methods are summarized in table 4. In general, the proposed method gives results in the same order of magnitude as the previous methods. Nevertheless, the results of the previous methods from the literature might be too conservative according to practical experience.
Table 4. Maximum scour depth estimates by four different methods.
Method |
Maximum Scour
Depth for Case 2,
b = 2 m |
Maximum Scour
Depth for Case 3,
b = 1 m |
Arneson and Abt, figure 3 |
6.58 |
6.10 |
Lyn, figure 5 |
4.88 |
4.88 |
Umbrell et al., figure 7 |
8.29 |
9.52 |
Proposed method, figure 60 |
2.87 |
2.12 |
Example 2 (Scour Evaluation)
For a field scour evaluation for the previous example, if the scour depth is measured at the upstream deck edge, it is about -4.89 ft (-1.49 m), as seen in figure 77.
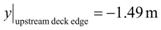 |
| 1 m = 3.28 ft |
Figure 77. Equation. Scour depth at the upstream deck edge.
According to figure 32, the corresponding maximum ys is 9.45 ft (2.88 m), as seen below in figure 78.
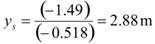
|
| 1 m = 3.28 ft |
Figure 78. Equation. Maximum scour depth solution.
By comparing this scour depth with the designed foundation dimensions, a designer can determine whether or not the scour is
critical and poses a risk to the structure.
CHAPTER 6. FURTHER RESEARCH NEEDS
This study is based on experiments in a rectangular flume using uniform sands with clear water at critical approach velocity and decks with rectangular girders that are far above the river bed. The results from the study are the maximum scour value and scour profiles. For cost efficiency, it would be beneficial to conduct additional research including the following:
-
Temporal variation of bridge pressure flow scour in clear water: The methods proposed in this study are for computing equilibrium scour, which requires a long flow duration in flume experiments. The corresponding duration required to reach equilibrium scour in field conditions may be considerably larger than the duration of a design flood. Thus, further research is needed to estimate the variation in scour depth with respect to time.
-
Clear Water Scour with Approach Velocity Less Than Critical Velocity: The proposed method assumes that the approach velocity is at critical velocity, which results in the maximum scour depth. When the approach velocity is less than the critical velocity, the scour should be smaller. Further research is needed to quantify this difference for various approach velocities.
-
Clear Water Scour with Sand Mixtures: The proposed method is based on experiments using uniform bed materials. Heterogenous bed materials should have an armoring effect, which would reduce the scour depth in accordance with the median diameter. Further research is needed to quantify the effect of gradations in sediments.
-
Effect of Girder Shapes: This study emphasized decks with rectangular girders. Although it was not described herein, a streamlined bridge deck shape was also preliminarily tested during the study. It showed a significantly shallower scour hole than those beneath the bridges with rectangular girders. Additional research is needed to study the effect of different deck and girder shapes on scour.
-
Pier Scour Under Bridge Pressure Flow Conditions:The experiments in this study were conducted without piers. The current practice superposes a general scour and a local pier scour. This may not be a good assumption because of nonlinear interactions between a pier and a fluid under pressure flow conditions. Hence, further research is required to understand the nonlinear effects on pier scours under pressure flow conditions.
-
Live-Bed Scour in Bridge Pressure Flows: The proposed method for clear water scour is governed by critical velocity. Nevertheless, most river flows are sediment-laden flows where scours are governed by sediment transport capacity. Hence, a study on live-bed scour is necessary.
Due to the limitations of the experiment documented in this study, engineering judgment should be exercised when developing new designs or retrofitting existing structures in natural channels using the proposed method.
CHAPTER 7. CONCLUSIONS
Several conclusions can be drawn from this study. A set of high-quality data on bridge pressure flow scour have been obtained. The data show that the horizontal scour depends on deck width. The scour starts at about 1 deck width upstream of the bridge, as shown in figure 28, and the deposition starts at about 2.5 deck widths downstream of the bridge, as shown in figure 31.
A second conclusion is that a similarity scour profile exists where the horizontal length is normalized to the deck width and the vertical dimension to the maximum scour depth, as shown in figure 22 and figure 23. In addition, the similarity scour profile is mostly independent of the number bridge girders and sediment size. The dataset obtained can be a benchmark for further studies, and the similarity relations can be used for field scour evaluation.
An analytical solution for pressure flow scour has been presented. The theoretical study showed that the study of bridge flow scour can be divided into three cases: case 1 is open channel flow, while cases 2 and 3 are rapidly varied pressure flow. For pressure flow, the maximum scour depth can be described by a scour number and an inundation number, as in figure 51 or
figure 53. The maximum scour depth decreases with increasing sediment size, but it increases with deck inundation and thickness. The analytical solution can predict the maximum scour and a corresponding scour profile. Since the analytical
solution is based on the energy and mass conservation laws, it is expected to be applicable to prototype flows without scaling effects.
The proposed method has been validated with the flume data, and an application procedure with examples has been presented.
Nevertheless, engineering judgment is required in practice when developing new designs or retrofitting existing structures in natural channels.
APPENDIX A. MAXIMUM SCOUR DEPTH FOR CASE 1
Referring to figure 38, when the scour reaches its equilibrium state, the downstream flow is uniform with a critical bed shear
stress. If the uniform flow is described by the Manning equation and the critical bed shear stress by the Shields diagram, the downstream flow depth is the same as that in clear water contraction scour.(4)
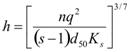
Figure 79. Equation. Downstream flow depth.
Where:
h = The downstream flow depth.
n = Manning coefficient.
q = Unit discharge.
The Ks for sands can be found with the equation in figure 80.(7)
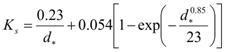
Figure 80. Equation. Critical Shields number approximation by Guo.
In which:
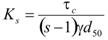
Figure 81. Equation. Shields number.
Where:
τc = The critical bed shear stress.
The dimensionless diameter, d*, is defined in figure 82.
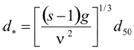
Figure 82. Equation. Dimensionless diameter.
Where:
v = The kinematic viscosity of water.
h = The downstream flow depth, which is the available uniform flow depth after scour.
The scour depth can be found by the energy equation between points 1 and 2 in figure 38 where the datum is chosen at the maximum scour bed elevation (see figure 83).
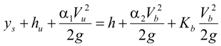
Figure 83. Equation. Energy equation between points 1 and 2.
Where:
α1 and α2 = Energy correction coefficients.
Kb = Entrance energy loss coefficient, which can be taken as 0.52 according to a box culvert experiment.(8) Note that the energy loss due to friction has been neglected because of the short distance between points 1 and 2.
The scour depth from figure 83 is then represented in figure 84 as follows:
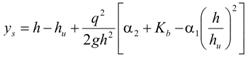
Figure 84. Equation. Scour depth.
In the figure, the relationship Vu = q/hu has been used. Theoretically, case 1 is well defined with figure 79 to figure 84. Practically, case 1 is only a short transition to case 2. This is because the upstream submerged portion of the bridge is not significant. As scour develops, the eroded materials will deposit somewhere downstream of the bridge. That sediment raises the tailwater and causes the downstream deck to become submerged.
APPENDIX B. DERIVATION OF PRESSURE UNDER BRIDGE DECK
The Bernoulli equation across streamlines is expressed below in figure 85.(9)

Figure 85. Equation. Bernoulli equation across streamlines.
Where:
R = Local radius of curvature of a streamline.
n = Normal coordinate to the streamline and toward concave side.
The flow through the maximum scour cross section can be simplified with circular streamlines and constant velocity, Vb, as shown in figure 87. Applying figure 85 to the vertical line gives figure 86 as follows:
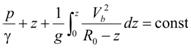
Figure 86. Equation. Bernoulli equation applied to circular streamlines.
The coordinates n and z are collinear along the vertical line that passes through the maximum scour point.
R0 = The radius of curvature at the maximum scour point as shown in figure 81, and the local radius R = R0 – z at position z has been applied.
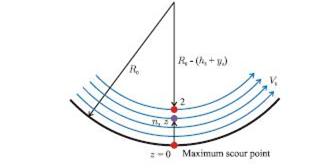
Figure 87. Illustration. Radii of curvature.
Integrating the equation in figure 86 gives figure 88.
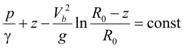
Figure 88. Equation. Integration of figure 86.
Applying the equation in figure 88 to point 2 where z2 = hb yields figure 89, which is valid for any velocity at point 2.
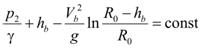
Figure 89. Equation. Bernoulli equation solved at point 2.
If Vb = zero from figure 39, the equation in figure 90 is generated as follows:
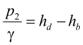
Figure 90. Equation. Pressure at point 2 when Vbequals zero.
The downstream free surface is taken as the reference since it is close to point 2. Substituting figure 90 and Vb = zero into figure 89 gives the integration constant seen in figure 91 as follows:
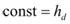
Figure 91. Equation. Solution for integration constant.
Substituting figure 91 into figure 89 and rearranging it gives the general equation at point 2, as shown in figure 92 as follows:
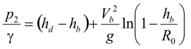
Figure 92. Equation. Pressure at point 2.
The curvature coefficient, Kp, is defined in the equation figure 93 as follows:
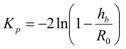
Figure 93. Equation. Curvature coefficient.
Through substitution, figure 92 becomes the equation seen in figure 94, in which the last term is called a curvature pressure. The parameter, Kp, represents the effect of the streamline curvature under the bridge. The equation in figure 93 is used in figure 41.
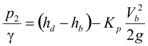
Figure 94. Equation. Pressure at point 2 with curvature coefficient simplification.
ACKNOWLEDGEMENTS
This study was supported by the FHWA Hydraulics Research and Development Program with contract No. DTFH61-04-C-00037. We thank Oscar Berrios for his diligent and dedicated work in running the tests and preparing some of the figures. We are grateful to Mr. Bart Bergendahl at FHWA, Kevin Flora at the California Department of Transportation, and Professor Dennis Lyn at Purdue University for their constructive suggestions.
REFERENCES
- Arneson, L.A. and Abt, S.R. (1998). "Vertical Contraction Scour at Bridges With Water Flowing Under Pressure Conditions," Transportation Research Record 1647, 10–17.
- Lyn, D.A. (2008). "Pressure-Flow Scour: A Reexamination of the HEC-18 Equation," Journal of Hydraulic Engineering, 134(7), 1015–1020.
- Umbrell, E.R., Young, G.K., Stein, S.M., and Jones, J.S. (1998). "Clear-Water Contraction Scour Under Bridges in Pressure Flow," Journal of Hydraulic Engineering, 124(2), 236–240.
- Richardson, E.V. and Davis, S.R. (2001). Evaluating Scour at Bridges: Fourth Edition, HEC-18, FHWA-NHI 01-001, United States Department of Transportation, Washington, DC.
- Neill, C.R. (1973). Guide to Bridge Hydraulics, University of Toronto Press, Toronto, Canada.
- Picek, T., Havlik, A., Mattas, D., and Mares, K. (2007). "Hydraulic Calculation of Bridges at High Water Stages," Journal of Hydraulic Research, 45(3), 400–406.
- Guo, J. (2002). Proceedings of the 13th IAHR-APD Congress, World Scientific, 2, 1096–1098.
- Jones, J.S., Kerenyi, K., and Stein, S. (2006). Effects of Inlet Geometry on Hydraulic Performance of Box Culverts, FHWA-HRT-06-138, United States Department of Transportation, Washington, DC.
- Young, D.F., Munson, B.R., Okiishi, T.H., and Huebsch, W.W. (2007). A Brief Introduction to Fluid Mechanics, 4th ed., John Wiley and Sons, Hoboken, NJ.
| 