• Federal Highway Administration >
• Publications >
• Research Publications >
• Hpc
• 97030 >
• Chap5.Cfm >
• High-Performance Concretes

High-Performance Concretes

A State-of-Art Report (1989-1994)

5  BEHAVIOR OF FIBER-REINFORCED CONCRETE

5.1  Introduction

High-Performance Fiber-Reinforced Concrete (HPFRC) results from the addition of either short discrete fibers or continuous long fibers to the cement based matrix. Due to the superior performance characteristics of this category of HPC, its use by the construction industry has significantly increased in the last 5 years. A very good guide to various portland cement-based composites as well as their constituent materials is available in a recently published book [Balaguru and Shah 1992]. The book provides information on fabrication, mechanical and long-term properties of concretes with short discrete fibers. It also covers special topics such as fiber reinforced cements and slurry-infiltrated fiber concrete. In 1992, the first international workshop on high performance fiber reinforced cement composites (HPFRCC) was held in Mainz, Germany [Reinhardt and Naaman 1992].

For highway pavement applications, concretes with early strength are attractive for potential use in repair and rehabilitation with a view towards early opening of traffic. The work conducted on high early strength fiber reinforced concrete (HESFRC) as a part of the SHRP C-205 project is reported in volume 6 of the SHRP reports [Naaman et al. 1993]. This report provides an extensive database and a summary of comprehensive experimental investigation on the fresh and mechanical properties of HESFRC. The control high early strength (HES) concrete (used with the fiber addition) were defined as achieving a target minimum compressive strength of 5,000 psi (35 MPa) in 24 hours, as measured from 4 x 8 in. (100 x 200 mm) cylinders.

This chapter is divided into two major sections. The first section deals with short discrete fiber reinforced concrete and the second section summarizes the recent developments in the use of continuous fibers as reinforcements to produce high performance fiber-reinforced structural concrete.

5.2  Discrete Fiber-Reinforced Concrete

5.2.1  Strength

The strength of the fiber reinforced concrete can be measured in terms of its maximum resistance when subjected to either compressive, tensile, flexural and shear loads. In field conditions, usually some combination of these loads is imposed; however for evaluation purposes, the behavior is characterized under one type of loading without the interaction of other loads. The strength under each individual type of loading is a useful indicator of the FRC material's performance characteristic for design consideration.

5.2.1.1  Compression

The compressive properties of fiber-reinforced concrete (FRC) are relatively less affected by the presence of fibers as compared to the properties under tension and bending.

The influence of fibers in improving the compressive strength of the matrix depends on whether mortar or concrete (having coarse aggregates) is used and on the magnitude of compressive strength. Studies prior to 1988 including those of Williamson [1974], Naaman et al. [1974] showed that with the addition of fibers there is an almost negligible increase in strength for mortar mixes; however for concrete mixes, strength increases by as much as 23%. Furthermore, Otter and Naaman [1988] showed that use of steel fibers in lower strength concretes increases their compressive strength significantly compared to plain unreinforced matrices and is directly related to volume fraction of steel fiber used. This increase is more for hooked fibers in comparison with straight steel fibers, glass or polypropylene fibers. The typical influence of fibers on the stress- strain curve of concrete composites is illustrated in Figs. 5.1 and 5.2.

Ezeldin and Balaguru [1992] conducted tests to obtain the complete stress-strain curves of steel fiber-reinforced concrete with compressive strengths ranging from 35 MPa to 84 MPa (5,000 to 12,000 psi). The matrix consisted of concrete rather than mortar. Three volume fibers fractions of 50 pcy, 75 pcy and 100 pcy (30 kg/m³, 45 kg/ m³ and 60 kg/ m³) and three aspect ratios of 60,75 and 100 were investigated. It was reported that the addition of hooked-end steel fibers to concrete, with or without silica fume, increased marginally the compressive strength and the strain corresponding to peak stress.

The effect of silica fume on the compressive properties of synthetic fiber-reinforced concrete was studied by Bayasi and Celik [1993] by testing 6 12 in. (150 300 mm) cylinders. Two fiber types were used: fibrillated polypropylene fibers and polyethylene-terphalate polyester fibers. Fiber volume fractions ranged from 0 to 0.6% and fiber length was 12 mm (0.5 in.). Silica fume was used as partial replacement of portland cement on an equal mass basis at 0, 5, 10 and 25%. Fibers had a relatively small favorable effect on the compressive strength. Both types of fibers improved the compressive behavior by enhancing the toughness. Furthermore, both types of fiber appeared to increase the strain at peak compressive stress. At 0.35 and 0.30 percent of polyester and polypropylene fiber content, respectively, use of silica fume enhanced the compressive strength and toughness of fiber concrete with an optimum content of 5 to 10 percent of weight of cement. Bayasi and Zeng [1993] reported that when polypropylene fibers with fiber lengths of 0.5 in. (12.5 mm) and 0.75 in. (19 mm) were used in volume fractions of 0.1, 0.3 and 0.5%, there was no significant effect on the compressive strengths.

Nakagawa et al. [1989] conducted compressive strength tests of concrete with short discrete carbon (both pitch-based type and PAN type), Aramid fibers and high strength Vinylon fibers. The tests were conducted on 100 x 200 mm (4 x 8 in.) cylindrical specimens. The volume percentages used were 1.86 and 3.05% for pitch type carbon fibers, 1.88 and 3.37% for Pan-type carbon fibers, 2.09 and 3.67% for Aramid fibers, and 2.00 and 3.40 for high strength Vinylon fibers. The results indicated that compressive strength tends to decrease when the fiber volume was increased. The effect of large volume of entrained air, due to the increase of fiber volume, had a significant influence on this reduction of strength.

Ezeldin and Lowe [1991], studied the compressive strength properties of rapid-set materials reinforced with steel fibers. The primary variables were (a) rapid-set cementing materials, (b) fiber type, and (c) fiber content. Four fiber types made of low-carbon steel were incorporated in this study. Two were hooked and one was crimped at the ends, and one was crimped throughout the length. Fibers were added in the quantities of 50, 75 and 100 lbs/yd³ (30, 45, and 60 kg/m³). The findings indicate that steel fibers can be successfully mixed with rapid-set materials up to a quantity of 75 lbs/yd³ (45 kg/m³). An increase in the compressive strength in the range of 5 to 25% within 24 hours was observed. The magnitude of the increase is dependent on the fiber shape and the content.

Zheng and Chung [1989], conducted compressive strength tests on 50 mm (2 in.) mortar cube specimens reinforced with short pitched-based carbon fibers (0.5% by weight of cement or 0.28% by volume of cement mortar) together with water reducing agent and an accelerating admixture. The results indicated tensile strengths of carbon fiber reinforced cement mortar increased by about 18% to 31% compared to the corresponding plain cement mortar values. The ductility was also improved.

5.2.1.2  Flexure

There are a number of factors that influence the behavior and strength of FRC in flexure. These include: type of fiber, fiber length (L), aspect ratio (L/d_f) where df is the diameter of the fiber, the volume fraction of the fiber (V_f), fiber orientation and fiber shape, fiber bond characteristics (fiber deformation). Also, factors that influence the workability of FRC such as W/C ratio, density, air content and the like could also influence its strength. The ultimate strength in flexure could vary considerably depending upon the volume fraction of fibers, length and bond characteristics of the fibers and the ultimate strength of the fibers. Depending upon the contribution of these influencing factors, the ultimate strength of FRC could be either smaller or larger than its first cracking strength.

Generally, there are three stages of the load-deflection response of FRC specimens tested in flexure and schematically they are shown in Fig. 5.3. The three stages are:

1. A more or less linear response up to point A. The strengthening mechanism in this portion of the behavior involves a transfer of stress from the matrix to the fibers by interfacial shear. The imposed stress is shared between the matrix and fibers until the matrix cracks at what is termed as "first cracking strength" or "proportional limit".
2. A transition nonlinear portion between point A and the maximum load capacity at point B (assuming the load at B is larger than the load at A). In this portion, and after cracking, the stress in the matrix is progressively transferred to the fibers. With increasing load, the fibers tend to gradually pull out from the matrix leading to a nonlinear load-deflection response until the ultimate flexural load capacity at point B is reached. This point is termed as "peak" strength.
3. A post peak descending portion following the peak strength until complete failure of the composite. The load-deflection response in this portion of behavior and the degree at which loss in strength is encountered with increasing deformation is an important indication of the ability of the fiber composite to absorb large amounts of energy before failure and is a characteristic that distinguishes fiber-reinforced concrete from plain concrete. This characteristic is referred to as toughness.

The nonlinear portion between A and B exists, only if a sufficient volume fraction of fibers is present. For low volume fraction of fibers (V_f < 0.5%), the ultimate flexural strength coincides with the first cracking strength and the load-deflection curve descends immediately after the cracking load, Fig. 5.4. Typical load-deflection curves of FRC beams observed experimentally for different types of fibers are shown in Figs. 5.5 and 5.6.

Two concepts are proposed in the literature for explaining the factors that affect the magnitude of the "first cracking strength or proportional limit". One concept relates the "first cracking strength" to the spacing of the fibers in the composite [Romualdi and Batson 1963; Romualdi and Mandel 1964]. The other concept is based on the mechanics of the composite materials and relates the "proportional limit" to the volume fraction of the fiber, aspect ratio and fiber orientation.

In the fiber spacing concept, it is stipulated that the volume fraction of fibers and fiber aspect ratio must be such that there is a fiber overlap; however, except for this, the fiber aspect ratio L/d_f which has a significant effect on the flexural strength of FRC is not a parameter in the fiber spacing approach. Experimental results by some investigators [Edington et al. 1974; Swamy and Mangat 1974] tend to show that the fiber spacing concept does not accurately predict the first cracking strength of fiber-reinforced concrete. Additional discussion of the spacing concept can be found in Hannant's book [Hannant 1978].

The law of composite materials is believed to be simple and is proven experimentally [Shah and Rangan 1971] to be more accurate for the prediction of first cracking strength in comparison with the fiber spacing concept. The composite materials approach is based on the assumptions that the fibers are aligned in the direction of the load, the fibers are bonded to the matrix, and the Poisson's ratio of the matrix is zero. In the law of composite materials, the effect of fibers on the cracking behavior of FRC composites can be viewed similarly to conventional reinforcing steel in concrete members. However, because the fibers are randomly distributed, an efficiency factor is commonly multiplied by the volume fraction of fibers to account for their random distribution. The efficiency factor was studied in the literature and was observed to vary between 40% and 80% [Romuldi and Mandel 1964; Nielsen and Chen 1968].

Because of the linear dependence of the ultimate flexural strength of FRC on the volume fraction of fibers and their aspect ratio, it could be stated that the ultimate flexural strength generally increases with the fiber reinforcing index, defined as the product of fiber volume fraction and aspect ratio (V_fL/d_f). Based on this observation, Shah and Rangan [1971] proposed the following general equation for predicting the ultimate flexural strength of the fiber composite:

  (5.1)

where f_cc is the ultimate strength of the fiber composite, f_m is the maximum strength of the plain matrix (mortar or concrete), A and B are constants which can be determined experimentally. For plain concrete, A = 1 and B = 0. The constant B accounts for the bond strength of the fibers and randomness of fiber distribution. Swamy et al. [1974a] established values for the constants A and B as 0.97 and 4.94 for the ultimate flexural strength of steel fiber-reinforced concrete and 0.843 and 4.25 for its first cracking strength.

Ezeldin and Lowe [1991] studied the flexural strength properties of rapid-set materials reinforced with steel fibers. The primary variables were (a) rapid-set cementing materials, (b) fiber type, and (c) fiber content. Four fiber types made of low-carbon steel were incorporated in this study. Two were hooked and one was crimped at the ends, and one was crimped throughout the length. Steel fibers were added in the quantities of 50, 75 and 100 lbs/yd³ (30, 45 and 6 kg/m³). An increase in the flexural strength was observed. The fiber efficiency in enhancing the flexural strength is controlled by the fiber surface deformation, aspect ratio, and fiber content. The results further indicate that steel fibers are very effective in improving the flexural toughness of rapid-set materials. Toughness indexes as high as 4 for I₅ and 9 for I₁₀ can be achieved with fiber contents of 75 lbs/yd³ (45 kg/m³).

A comparative evaluation of the static flexural strength for concretes with and without four different types of fibers: hooked-end steel, straight steel, corrugated steel, and polypropylene fibers was conducted by Ramakrishnan et al.[1989a]. The fibers were tested at 0.5, 1.0, 1.5 and 2.0% by volume. It was reported that maximum quantity of hooked-end fibers that could be added without causing balling was limited to 1.0 percent by volume. Compared to plain concrete, the addition of fibers increased the first cracking strength (15 to 90 percent) and static flexural strength (15 to 129 percent). Compared on equal basis of 1.0 percent by volume, the hooked-end steel fiber contributed to the highest increase, and the straight fibers provided the least appreciable increase in the above mentioned properties.

Johnston and Zemp [1991] investigated the flexural performance under static loads for nine mixtures, Table 5.1, using sets of 15 specimens for each mixture. Each set of 102 x 102 x 356 mm (4 x 4 x 14 in.) specimens were prepared from five nominally identical batches and tested under third point loading over a 305 mm (12 in.) span. First crack strengths defined in ASTM C 108 as the point on the load-deflection curve at which the form of the curve first becomes nonlinear, and ultimate strength based on the maximum flexural load (ASTM C 78) were established for the eight fibrous concretes, with only ultimate strength for the plain concrete control. The ultimate strengths based on the maximum load was only slightly greater (2.1% on average) than the first crack strength, with a maximum of 4.2% for mixture 3, containing 1.5% fibers. The deflection at maximum load was likewise little different from the first crack deflection. Trends or relationships involving the first crack strengths were therefore similar to those involving ultimate strengths. Note that this may not be the case for fiber-matrix combinations that produce multiple peaks on the load-deflection curve with the maximum load at deflection much higher than the first crack deflection [Johnston and Carer 1989]. The results of Johnston's work indicated that increasing the fiber content from 0.5 to 1.5% had a significant beneficial effect on the first crack (and ultimate) strengths despite the negative influence of increasing w/c and w/(c+f). The increase in first crack strength of 31%, unadjusted for the differences in w/c and w/(c+f) is quite large, since it is widely believed that increasing fiber content has only a minor effect on first crack strength for many of the types of fiber in current use. With the adjustment in w/c and w/(c+f), for 1.5% of SW(75) fibers in Table 5.1, the increase is 63% over the value for 0.5% of the same fibers.

Although increasing aspect ratio (V_f L/d_f) has long been recognized as a positive influence on performance because of the improved resistance to pull-out of the fibers from the matrix, any benefit for the smooth wire (SW) fiber used by Johnston and Zemp [1991] was obscured by the increase in w/c and w/(c+f) needed to maintain the workability. After adjustment to allow for the differences in w/c and w/(c+f), strengths were seen to increase slightly with increasing aspect ratio as expected from the consideration of the pullout resistance. The effect of the aspect ratio was quite small compared with that of the fiber content.

A change in fiber type often involves a change in aspect ratio. Johnston and Zemp [1991] investigated the effect of the fiber type. The results indicated that for particular fiber types, smooth and deformed wire fibers (SW and SDW) the effect - although small compared to the fiber content - is slightly superior to melt extract (ME) and slit sheet (SS) fibers of the same aspect ratio. This does not means that all wire fibers will necessarily be superior to all melt extract or slit sheet fibers because fiber development is a continuous ongoing process.

Fiber content seems to be the parameter that is of primary importance in determining the first-crack and ultimate strengths under static flexure loading. Fiber aspect ratio and fiber type are of secondary importance in practical concretes where increasing the aspect ratio or changing the type (steel composition, surface area, surface texture, etc.) in a manner that increases water demand may tend to counteract any improvements in strength attributable to changes in these fiber parameters.

Balaguru et al. [1992] conducted flexural tests on deformed steel fibers reinforced concrete beams. The variables investigated were fiber type, length and volume fraction, and matrix composition. The results indicate that fiber content in the range of 30 to 60 kg/m (50 to 100 lbs/yd³) provide excellent ductility for normal strength concrete. The fiber content has to be increased to about 90 kg/m³ (150 lbs/yd³) for high strength concrete. Hooked-end fiber geometry provides better results than corrugated and deformed-end geometry. Fiber length, in the range of 30 to 60 mm (1.18 to 2.36 in.) does not have any significant effect on toughness for hooked-end fibers. Ductile behavior can be obtained using 120 kg/m³ (200 lbs/yd³) of fibers, even for concretes containing 20 percent silica fume by weight of cement. The load-deflection curves for normal strength concrete beams and high strength concrete beams with 30 mm long hooked-end fibers are shown in Figs. 5.7a and 5.7b. It has been reported [Ashour 1993] that steel fibers also enhance the strength and ductility of high strength concrete beams.

The effect of silica fume on the flexural strength of synthetic fiber-reinforced concrete was studied by Bayasi and Celik [1993]. The specimens were 100 x 100 x 350 mm (4 x 4 x 14 in.) and were subjected to a four point (1/3 point) flexural load-deflection behavior test over a span of 300 mm (12 in.) according to ASTM C 78 and C 108. Two fiber types were used: fibrillated polypropylene fibers and polyethylene-terphalate polyester fibers. Fiber volume fractions ranged from 0 to 0.6% and fiber length was 12 mm (0.5 in.). Silica fume was used as partial replacement of portland cement on an equal mass basis at 0, 5, 10 and 25%. The results indicate that polyester fibers and polypropylene fibers have an inconsistent effect on the flexural strength but significantly increases the flexural toughness and the post-peak resistance of concrete. These improvements continues as fiber volume increases, except in ultimate strength, for which it starts to decrease beyond fiber volume of 0.35 percent. It was also shown that silica fume enhances toughness and post-peak strength of plastic fiber concrete.

Bayasi and Zeng [1993] proposed that flexural behavior of polypropylene fiber be characterized by the post-peak flexural resistance (load or stress). It was found that, for volumes equal or less than 0.3 percent, 19 mm (0.75 in.) long fibers were more favorable for enhancing the post-peak resistance. For 0.5 percent volume, 12.5 mm (0.5 in.) long fibers were more effective. The typical results are shown in Fig. 5.8.

Balaguru [1992] also investigated the flexural strength and the flexural load-deflection behavior of polymer-fiber reinforced rapid-setting concrete. The test variables were the matrix type and fiber type. The first product was a portland cement with a pozzolanic addition termed as PY. The second product was a blend of magnesium oxide and ammonium di-hydrogen phosphate with a small amount of fly ash identified as SE. The fibers were made of fibrillated polypropylene and single-filament nylon 6. Typical load-deflection curves are shown in Fig. 5.9 indicate that post-peak drop is steeper for polymer fibers as compared to steel fibers. This should be expected because of the low modulus of elasticity of polymers fibers.

Nakagawa et al. [1989] conducted flexural tests of concrete with short discrete carbon (both pitch-based type and PAN type), Aramid fibers and high strength Vinylon fibers. The specimens had a crossection of 50 x 100 mm (2 x 4 in.) and the length of the specimens was 1,100 mm (43 in.). The specimens were loaded with two point loads with a shear span of 300 mm (11.8 in.). The constant moment region was 300 mm (11.8 in). The volume percentages used were 1.86 and 3.05 for pitch type carbon fibers, 1.88 and 3.37 for Pan-type carbon fibers, 2.09 and 3.67 for Aramid fibers, and 2.00 and 3.40 for high strength Vinylon fibers. The results indicated that limit of proportionality (LOP) and the modulus of rupture (MOR) increased with fiber volume, and the strength of the fiber used. The typical load-deflection results for various types of fibers are shown in Fig. 5.10.

Zheng and Chung [1989] conducted flexural tests on 4 x 4 x 16 cm (1.57 x 1.57 x 6.30 in.) beams with third point loading. The mortar specimens were reinforced with short pitched-based carbon fibers (0.5% by weight of cement or 0.28 volume % of cement mortar) together with water reducing agent and an accelerating admixture. The results indicated that flexural strengths of carbon fiber reinforced cement mortar increased by about 89% to 112% compared to the corresponding strengths of plain cement mortar.

Cementitious composites with higher volume percentages (in the range of 12 to 16 percent) of fibers have been investigated to exploit the beneficial effects of fibers. These cementitious composites termed as SIFCON (Slurry infiltrated concrete) were investigated in an experimental study dealing with the behavior of reinforced concrete beams containing a SIFCON matrix [Fritz et al. 1992]. The results indicated that the presence of SIFCON in overreinforced concrete beams led to ductility indexes exceeding three times those obtained without it. Crack widths and spacing were more than an order of magnitude smaller than in conventional reinforced concrete. The experimental results also suggested that there is no need for stirrups in flexural members with SIFCON matrix.

One promising new development uses steel fiber mats to reinforce concrete matrix. This new approach, called SIMCON (Slurry infiltrated mat concrete), produces concrete components with extremely high flexural strength [Hackman et al.1992; Krstulovic-Opara et al. 1994]. The advantage of steel fiber mats over a large volume of discrete fibers is that the mat configuration provides inherent strength and can utilize fibers with much higher aspect ratios. The fiber volume is less than half that required for SIFCON (slurry infiltrated fiber concrete), while achieving similar flexural strength and energy absorption capacity. The typical aspect ratios for FRC range from 40 to 100, although special handling procedures may be required as the aspect ratio approaches 100. SIMCON utilizes fibers with aspect ratios exceeding 500. Since the mat is already in a pre-formed shape, handling problems are minimized and balling does not become a factor. Hackman et al.[1992] conducted flexural tests with SIMCON. The fibers were manganese carbon steel, approximately 9.5 in (241 mm) with an equivalent diameter of 0.010 to 0.020 in.(0.25 to 0.50 mm). Stainless steel mats were also produced using a 9.5 in. (241 mm) long fiber with an equivalent diameter of 0.010 to 0.020 in. (0.25 to 0.50 mm). The fiber volume percent for the manganese carbon steel ranged from 1.2 to 3.6, while the stainless steel mats were packed to a density of 5.7 percent. Two specimens of 2 x 4 x 20 in. (50 x 100 x 500 mm) of SIMCON were tested in flexure. For comparison purposes, three SIFCON 2 x 4 x 14 in. (50 x 100 x 350 mm) beam specimens were also prepared with SIFCON slurry containing 14 percent 1.0 in.(25 mm) long 304 stainless steel fibers. The flexural tests were conducted in accordance with ASTM C 1018, using a third-point loading and a 12 in. (300 mm) span. The SIMCON composites with fiber mats of only 3.3 and 3.6 volume percent provided an ultimate flexural strength of roughly 75% of the flexural strength of SIFCON specimens at 25 percent of the fiber volume used in SIFCON. With a 5.7 volume percent of stainless steel fiber mat, the resulting SIMCON composite exhibited an average of 85% of the flexural strength of SIFCON with a 41% of the fiber volume. Figs. 5.11a to 5.11c show the load-deflection behavior of various SIFCON and SIMCON composites. The superior performance of the SIMCON over SIFCON is related to the bonding of the mat fibers in the composite. In the standard SIFCON, the relatively short embedment length of 1 in. (25 mm) results in fiber pullout as the primary failure mode. In the SIMCON composites, the failure mode comprises of multiple cracks and ultimate failure occurs through fiber breakage in the high tensile stress zones of one or more of the crack planes. In the mat reinforced composites, the yield strength of the steel is fully utilized.

5.2.1.3  Tensile and Splitting Tensile

The failure in tension of cement-based matrices is rather brittle and the associated strains are relatively small in magnitude. The addition of fibers to such matrices, whether in continuous or discontinuous form, leads to a substantial improvement in the tensile properties of the FRC in comparison with the properties of the unreinforced matrix. The enhancement of the properties is particularly noticeable.

Most investigations in the field of FRC derive tensile properties of the composite indirectly on the basis of observations from flexural tests or split cylinder tests. This is because there are difficulties associated with the interpretation of results obtained from direct tension tests. The difficulties are due to differences in specimen sizes, specimen shapes, instrumentation and methods of measurement. As yet, no standard test specimen is available for direct tension tests. As such, the observed stress-strain or force-elongation curve in direct tension is expected to vary, depending on the size of the specimen, stiffness of the testing machine, gauge length used to calculate strains and the number of cracks developed within the gauge length. The primary difficulty in characterizing the tensile response of FRC composites is that the post cracking behavior is generally dominated by the widening of a single major crack as observed in several experimental studies [Visalvanich and Naaman 1983; Gopalaratnam and Shah 1987]. The concentration of deformation at the crack location leads to a non-uniform definition of strains in the cracked region which depends on the prescribed gauge length.

The stress-strain or load-elongation response of fiber composites in tension depends mainly on the volume fraction of fibers. In general, the response can be divided into two or three stages, respectively, depending on whether the composite is FRC (fiber volume less than about 3%) or Slurry Infiltrated (SIFCON) where the volume of fibers normally varies between 5% and 25%. Typical stress-strain or load-elongation curve for SIFCON and conventional FRC composites are shown in Figs. 5.12 and 5.13.

Before cracking, the composite (both SIFCON and FRC) can be described as an elastic material with a stress-strain response very similar to that of the un-reinforced matrix. Several approaches can be used to predict the main characteristics of the tensile stress-strain curve of fiber composites in the first linear stage before cracking. These include, the mechanics of composite materials, fracture mechanics, damage mechanics, and empirical approaches. Using the mechanics of composite materials, the tensile stress in the composite at cracking can be predicted from the following equations [Naaman 1987]:

  (5.2)

where s_cc is the tensile strength of the un-reinforced matrix, V_f and L/d_f, are the volume fraction and aspect ratio of fibers respectively, a₁ is a bond coefficient representing the fraction of bond mobilized at matrix cracking strain, and a₂ is the efficiency factor of fiber orientation in the uncracked state of the composite. Equation (5.2) shows that a slight improvement in the first cracking strength is expected at low volume fraction of fibers.

After cracking and in bridging the cracked surface, the fibers tend to pull out under load resulting in a sudden change in the load-elongation or stress-strain curve. If the maximum postcracking stress is larger than the cracking stress, such as in SIFCON (Fig. 5.12), then a second stage of behavior can be identified as the multiple cracking stage, and corresponds to the portion of the load-elongation curve that joins the cracking stress point to the maximum postcracking stress point (peak point on the curve). Beyond the peak point, a third stage of behavior exists characterized by failure and/or pullout of the fibers about a single critical crack. The corresponding descending branch of the load-elongation curve can be steep or of moderate slope depending on the fiber reinforcing parameters and whether a brittle or ductile failure occurs. Along stages I and II (Fig. 5.12), the elongation of the composite (measured along a defined gage length) can be transformed into equivalent strain. However, along stage III, the elongation corresponds primarily to the opening of a single critical crack and cannot be transformed into strain since crack opening is independent of the gage length.

The multiple cracking stage described above occurs only if the maximum postcracking stress is larger than the cracking stress; otherwise, in the case of conventional FRC, with a relatively small volume fraction of fibers, the second portion of the curve vanishes and is replaced by a sudden drop in the load-elongation curve joining the cracking load to the postcracking load. Hence the load-elongation response is reduced to two main parts (stages I and II) as illustrated in Figs. 5.13a and 5.13b. The curve of Fig. 5.13 is for high modulus fibers such as steel fibers, while the curve of Fig. 5.13b is for low modulus fibers such as polypropylene. A comparison of actual stress-elongation curves of steel fiber reinforced mortar and SIFCON is shown in Fig. 5.14.

The postcracking strength increases with increasing bond strength, aspect ratio and volume fraction of fibers. Several empirical equations were derived in the literature to calculate the ultimate strength of fiber composite in tension [Gasparini et al. 1989; Lim et al. 1987; Naaman et al.1974; Naaman 1987]. Almost all equations expressed the ultimate tensile strength s_pc in linear function of the fiber reinforcing index V_f L/d_f and fiber bond strength i_u as follows:

where k is a constant (k < 1.0) that takes into account the orientation, bond, and distribution characteristics of the fibers.

Experimental tests on splitting tensile strength of FRC are not as numerous as tests conducted in direct tension, flexure and compression. However, the same main factors that affect the behavior of FRC in direct tension, flexure and compression are expected to affect its behavior in splitting tensile mode; namely, the volume fraction, the aspect ratio, and the bond characteristics of fibers. Increasing the volume fraction of fibers and/or increasing their aspect ratio increases the splitting tensile strength of the fiber composite. Also, hooked and deformed fibers are expected to offer better splitting tensile resistance compared to straight or non-deformed fibers.

It is now generally accepted that the type and amount of fibers currently used do not significantly enhance the first cracking stress of the fiber reinforced composite. This is demonstrated in Fig. 5.16, where the tensile stress-strain curves for concrete reinforced with two types of fibers are shown. Note that the first cracking stress was observed to be the same, regardless of the volume and type of fibers.

Fribrillated continuous uniaxial polypropylene fiber specimens were manufactured by means of a pultrusion process by Krenchel and Stang [1988]. Specimens were manufactured with either epoxy or cement-based materials and tested in uniaxial tension at Northwestern University [Mobasher et al. 1990b]. Fig. 5.16 shows composite stress-strain curve for a set of specimens as well as the corresponding calculated matrix contribution by rule of mixtures. The tensile strength of the matrix can be as high as 15 MPa (2,150 psi), and even at an average strain of 2 percent, the matrix contributes about 8 MPa (1,150 psi) of tensile stresses. The development of cracking for these specimens was studied using the fluorescent microscopy and laser holography [Mobasher et al. 1990a, 1990c]. It was observed that when the load-displacement curve reached a distinct change in slope from an elastic to a semi-plastic response, the contribution of the matrix reached its maximum value. At this point distributed microcracks seemed to localize into macrocracks.

Many of the current applications of fiber reinforced concrete involve the use of fibers ranging around 1.0 percent by volume of concrete. Recently, it has been possible to incorporate relatively large volumes (ranging up to 15 percent) of steel, glass, and synthetic fibers in concrete. According to Shah [1991], analysis of results of tensile tests done on concretes with glass, polypropylene and steel fibers, indicate that with such large volume of aligned fibers in concrete, there is substantial enhancement of the tensile load carrying capacity of the matrix. This may be attributed to the fact that fibers suppress the localization of micro-cracks into macro-cracks and consequently the apparent tensile strength of the matrix increases.

Nakagawa et al. [1989] conducted tensile strength tests of concrete with short discrete carbon (both pitch-based type and PAN type), Aramid fibers and high strength Vinylon fibers. The direct tensile tests were conducted on dog-bone shaped specimens. The critical section was 30 mm (1.18 in.) wide, 80 mm (3.15 in.) in length and 12 mm (0.5 in.) in thickness. The volume percentages used were 1.86 and 3.05 for pitch type carbon fibers, 1.88 and 3.37 for Pan-type carbon fibers, 2.09 and 3.67 for Aramid fibers, and 2.00 and 3.40 for high strength Vinylon fibers. The results indicated that ultimate tensile strength increased with the increase in the fiber volume.

Zheng and Chung [1989] conducted tensile tests on briquette mortar specimens reinforced with short pitched-based carbon fibers (0.5% by weight of cement or 0.28 volume % of cement mortar) together with water reducing agent and an accelerating admixture. The results indicated tensile strengths of carbon fiber reinforced cement mortar increased by about 113% to 164% compared to the corresponding strengths of plain cement mortars.

5.2.1.4  Shear Strength

Shear failure can be sudden and catastrophic. This is true for critical sections where, due to construction constraints, little or no reinforcing steel may be placed. For more than 30 years, fiber reinforced concrete (FRC) has been the object of studies dealing with various loading conditions including compressive, flexural and tensile loadings. The use of fibers to improve the shear behavior of concrete is also promising; however, reported research efforts on the shear behavior of FRC are limited [Valle 1991]. Tests performed to study the shear behavior of FRC can be categorized into two general groups: direct shear tests, and tests on beams and corbels. The direct shear tests are required to understand the basic transfer behavior of concrete, while the tests on beams and corbels are necessary to understand the behavior of structural members reinforced with fibers.

The investigations on direct shear behavior include those of Swamy et al.[1987], Barr [1987], and Tan and Mansur [1990]. Shear tests involving corbels have been reported by Fattuhi [1987], and Hara and Kitada [1980]. A number of studies have reported combined shear and flexural tests on beams to investigate the improvements in the behavior due to the addition of steel fibers [Ward and Li 1990].

From these studies, it can be stated that the addition of fibers generally improves the shear strength and ductility of concrete. It has been reported that the stirrups as shear reinforcement in concrete members can be partially or totally replaced by the use of steel fibers [Lim et al. 1987; Mansur et al. 1986]. Most of the work has been limited to concretes of normal strength. The lack of research in this area is even greater for FRC involving high strength concrete.

Valle and Buyukozturk [1993] reported the results of an investigation on the strength and ductility of fiber reinforced high strength concrete under direct shear. Three parameters were investigated: (i) concrete type — high strength versus normal strength concrete, (ii) type of fiber — steel versus polypropylene fibers and (iii) the presence of steel stirrups crossing the shear plane. The average strengths were 4,500 psi (31.5 MPa) for the normal strength concretes and 9,000 psi (63 MPa) for the high strength concretes. The direct shear transfer behavior of fiber reinforced concrete was investigated through testing of initially uncracked pushoff specimens. The specimens had dimensions of 21 x 10 x 3 inches (525 x 250 x 75 mm), with a shear plane of 30 in² (18,750 mm²). In general, fibers proved to be more effective in high strength concrete than in normal strength concrete, increasing both ultimate load and overall ductility (Figs. 5.17a and 5.17b). Greater shear strength increases were found with fiber reinforced high strength concrete specimens (60% with steel and 17% with polypropylene fibers) than with fibers reinforced normal strength concrete specimens (36% with steel fibers and no increase with polypropylene fibers) when compared to the strengths of their respective unreinforced plain concrete specimens. The enhancement performance of fibers in high strength concrete is attributed to the improved bond characteristics associated with the use of fibers in conjunction with high strength concrete. For the specimens with steel fibers, significant increases in ultimate load and ductility were observed. With polypropylene fibers, a lower increase in ultimate load was obtained when compared to the increase due to steel fibers. Ductility of the polypropylene fiber reinforced specimens was greater than that of the steel fiber reinforced specimens. In the tests involving the combination of fibers and conventional stirrups, slight increases in ultimate load with major improvements in ductility were observed in comparison to the corresponding values for plain concrete specimens with conventional stirrups.

More research, both experimental and analytical is needed to develop a better understanding of shear behavior of composites and members with different types of fibers. The research should utilize metallic as well as non-metallic fibers.

5.2.2  Deformations

Information on deformation characteristics is essential for estimating the serviceability limits and the energy absorption capacity of FRC materials.

5.2.2.1  Modulus of Elasticity

The modulus of elasticity of a material, whether in tension, compression, or shear, is a fundamental property that is needed for modeling mechanical behavior in various structural applications. Tests have been devised to measure the moduli of elasticity of a given material. For pure materials, such as steel or glass, observed experimental values are tabulated once and for all, then used in practice. However, for FRC composites made out of at least two different materials, the modulus of elasticity depends on various parameters.

Numerous studies have addressed the modulus of elasticity of composite materials. They lead to numerous models that range from the very simple to the very sophisticated. Among the simplest models for composites made out of two different materials, the upper- and lower-bound solutions or a combination of them (described below) only depend on the volume fraction and the modulus of each material. More advanced models developed for fiber reinforced composites include, in addition, the properties of the interface between the two materials, whether the fibers are discontinuous or not, the distribution and orientation of the fibers, the aspect ratio (length to diameter) of the fiber, and the like.

The most common and the simplest models to predict the modulus of elasticity of FRC as a composite made out of two materials are the upper-and the lower-bound solutions or an arithmetic combination of both. They are described in details in many textbooks on composite materials and only the final solution is given below:

The upper-bound solution assumes that the fibers are continuous and oriented in the direction of loading along which the modulus of elasticity is needed. It leads to the following equation:

in which the subscripts c, L, f, and m stand respectively for composite, longitudinal, fiber, and matrix.

The lower bound solution assumes that the fibers are lumped with their axis normal to the direction along which the modulus is measured. It leads to the following equation:

in which the subscript T stands for transverse.

For a composite with randomly oriented fibers, Halpin and Tsai [1969] suggested an equation based on a combination of Eqs. (5.4) and (5.5). Although their predictions of longitudinal and transverse moduli were different from the above upper- and lower-bound solutions, their equation can be used as a first approximation with the above equations. It is given by:

Examination of Eqs. (5.4) to (5.6) shows that for the same volume fraction of fibers, steel fibers should improve the modulus of elasticity of the composite more than glass fibers (E_steel = 3 E_glass). Also, polypropylene fibers having a modulus of elasticity lower than that of concrete should lead to a decrease in the elastic modulus of the composite. However, for the range of fiber volume V_f normally used in practice, the increase or decrease in E_c is expected to be of the same order as the variability in the experimental data. The same is also true of the flexural stiffness of FRC composites.

Experimental studies [Fanella and Naaman 1985; Shah et al. 1978] have shown that the addition of fibers have only a slight effect on the ascending branch (modulus of elasticity) of the stress-strain curve of the composite. Investigators have also observed that the effect of adding fibers up to 4% by volume is small and linear for composites tested in flexure [Nielsen and Chen 1968; Edington et al. 1974; Ramakrishnan et al. 1989a], direct tension [Nielsen and Chen 1968; Edington et al. 1974; Mangat and Azari 1985] and compression [Nielsen and Chen 1968; McKee 1969]. Results showing the influence of steel fibers on the flexural stiffness of fiber composites is shown in Fig. 5.18.

Ezeldin and Lowe [1991] used three different amounts (30, 45 and 60 kg/m³ or 50, 75 and 100 lbs/yd³) of steel fibers in concretes with strengths ranging from 35 to 85 MPa (5,000 to 12,000 psi) to obtain the secant modulus of elasticity under compression. It was found that there was a marginal increase in the modulus of elasticity with the addition of steel fibers.

A comprehensive investigation on the modulus of elasticity of fiber-reinforced cement-based composites was conducted at the University of Michigan [Najm and Naaman 1992]. The results indicate that, although the factors suggested in Eqs. (5.4) to 0(5.6) above do influence the modulus of elasticity of the composite, other factors such as the length or aspect ratio of the fibers, their orientation, and the bond at the fiber matrix interface also have noticeable influence. It should be noted, however, that unless the fiber content is very large (more than 3% by volume), the approximate equation should give adequate results in all cases. Additional precision may not be warranted when compared to the variability usually encountered in the test results.

For the range of fiber volume normally used in practice, the dynamic modulus of fiber-reinforced concrete is little different from that of the plain, unreinforced concrete. Tests conducted by Swamy and Mangat [1974] have shown that the dynamic modulus of FRC reinforced with up to about 2% by volume of steel fibers varied within 5% of the control unreinforced matrix. Hence, the conventional solutions for the static elastic modulus also apply for the dynamic modulus of fiber-reinforced concrete.

Nakagawa et al. [1989] conducted tests for tensile modulus of elasticity of concrete with short discrete carbon (both pitch-based type and PAN type), Aramid fibers and high strength Vinylon fibers. The direct tensile tests were conducted on dog-bone shaped specimens. The critical section was 30 mm. (1.18 in.) wide, 80 mm (3.15 in.) in length and 12 mm (0.5 in.) in thickness. The volume percentages used were 1.86 and 3.05 for pitch type carbon fibers, 1.88 and 3.37 for Pan-type carbon fibers, 2.09 and 3.67 for Aramid fibers, and 2.00 and 3.40 for high strength Vinylon fibers. The results indicated that tensile modulus of elasticity increased with the increase in the fiber volume.

5.2.2.2  Creep and Shrinkage

Based on limited experimental data, the ACI committee 544 report [1982] indicates that wire fiber reinforcement has no significant effect on the creep behavior of portland cement mortar. However, recent results on the creep characteristics of FRC appear to contradict the above statement.

Creep tests conducted by Balaguru and Ramakrishnan [1988] in accordance with ASTM C 512 on steel fiber reinforced concrete (V_f = 0.6%, L/d_f = 100) subjected to a sustained load between 19% and 25% of the compression strength (stress to strength ratio between 0.19 and 0.25) showed that the creep strains were consistently higher than those of plain concrete. Also, creep tests conducted by Houde et al. [1987] on polypropylene and steel fibers showed that the addition of fibers increases the creep strains of the fiber composite by about 20% to 30% in comparison with the unreinforced matrix.

Unlike the observation made by Balaguru and Ramakrishnan [1988] and Houde et al. [1987], Mangat and Azari [1985] reported reduction in the creep strains with increasing content of steel fibers in comparison with plain concrete. For instance, at 3% by volume of fibers and at stress to strength ratio of 0.3, a reduction of about 25 % in creep strain compared to plain concrete is achieved after 90 days. However, it was observed that the steel fibers were less effective in restraining the creep at high stress to strength ratio (equal to 0.55) in comparison with low stress to strength ratio (equal to 0.33). The low effectiveness of steel fibers in decreasing the creep strains at large stress to strength ratio was attributed to the reduced interfacial bond characteristics of the fibers under creep. Large stress to strength ratios increase the lateral strains and hence decrease the interfacial pressure between the fibers and the surrounding concrete. This in effect reduces the restraint to sliding action between the fibers and the concrete matrix and results in larger creep strains.

The same factors that influence the shrinkage strain in plain concrete influence also the shrinkage strain in fiber reinforced concrete; namely, temperature and relative humidity, material properties, the duration of curing and the size of the structure. The addition of fibers, particularly steel, to concrete has been shown to have beneficial effects in counterbalancing the movements arising from volume changes taking place in concrete, and tends to stabilize the movements earlier when compared to plain concrete.

The effect of fibers in restraining the free drying shrinkage strains was found to be insignificant [Lim et al. 1987; Shah and Grzybowski 1989] or to cause a slightly smaller shrinkage than that of plain concrete [Paul et al. 1981; Balaguru and Ramakrishnan 1988]. If the purpose of fibers is only to restrain the free drying shrinkage strain, then the use of short and randomly distributed fibers is more beneficial than long fibers because of the larger number of fibers available in a given volume of concrete [Swamy 1985].

The primary advantage of fibers in relation to shrinkage is their effect in reducing the adverse width of shrinkage cracks [Swamy 1985; Lim et al. 1987; Shah and Grzybowski 1989]. Shrinkage cracks arise when the concrete is restrained from shrinkage movements. The presence of steel fibers delays the formation of first crack, enables the concrete to accommodate more than one crack and reduces the crack width substantially [Swamy 1985]. Tests conducted on restrained shrinkage behavior of FRC have shown that the addition of small amounts of steel fibers (0.25% by volume) reduced the average crack widths by about 20% [Shah and Grzybowski 1989] and the maximum crack width by about 50% [Lim et al. 1987] in comparison with unreinforced plain concrete. Comparing the effect of different types of fibers on the restrained shrinkage characteristics, one finds that polypropylene fibers are much less effective in reducing crack widths than steel fibers [Shah and Grzybowski 1989]. Randomly distributed fibers could enhance the mechanical properties of shrinkage-compensating concrete by restraining the composite uniformly in all directions without adversely affecting the mechanical properties of such composites. Tests conducted by Paul et al. [1981] on the effect of steel fibers on the expansion and drying shrinkage characteristics of expansive cement composites (Type K-conforming to ASTM C 845) have shown (Fig. 5.19) that the 7 day restrained expansion of the shrinkage-compensating concretes reinforced with straight fibers, crimped fibers and conventional steel bars were about 67%, 54% and 47% respectively of the expansion of unrestrained concrete.

High strength concretes with silica fume undergo early cracking when deformation is restrained. This phenomenon, which occurs even when concrete is protected against any evaporation, is attributed to autogenous shrinkage, because of the exceptionally low water-cement ratio (about 0.26). This phenomenon can be corrected by the use of fibers. Paillere et al. [1989] conducted shrinkage tests with two types of hooked fibers with ratios of lengths (in mm to diameter in hundredths of mm) of 30/60 and 50/50. The tests were conducted at fiber volume fraction of 0.8 percent. For each type of fiber, the optimum sand-aggregate ratio which gave the maximum slump was determined so as to magnify the shrinkage characteristics. The fiber concretes exhibited an autogenous shrinkage lower than the reference concrete and undergo cracking at a later age under restrained deformation.

Soroushian et al. [1993] investigated the effects of polypropylene fibers and construction operations on the plastic shrinkage cracking of concrete slabs. Polypropylene fibers at relatively low fiber volume fractions were observed to reduce substantially the total area and maximum crack width of slab surfaces subjected to restrained plastic shrinkage movements. The rate of screeding of fresh concrete was also a critical factor (particularly in plain concrete). Slower screeding rates led to reduced plastic shrinkage cracking.

5.2.2.3  Strain Capacity

The ability to withstand relatively large strains before failure, the superior resistance to crack propagation and the ability to withstand large deformations and ductility are characteristics that distinguish fiber-reinforced concrete from plain concrete. These characteristics are generally described by "toughness" which is the main reason for using fiber-reinforced concrete in most of its applications.

Unlike plain concrete specimens, the presence of fibers imparts considerable energy to stretch and debond the fibers before complete fracture of the material occurs. Toughness is a measure of the ability of the material to mobilize large amounts of post-elastic strains or deformations prior to failure. Typical load-deflection curves of FRC specimens in comparison with plain concrete specimens are shown in Fig. 5.20.

ASTM C 1018, provides Method A for evaluating the toughness of fiber reinforced composites through the use of a toughness index. The toughness index is calculated as the area under the load-deflection curve up to the prescribed service deflection divided by the area under the load-deflection curve up to the first cracking deflection. Three indexes are described in ASTM C 1018: I₅, I₁₀ and I₂₀ corresponding respectively to deflections of 3, 5.5 and 10.5 times the deflection at first cracking. These indices (computed as shown in Fig. 5.20) provide indications of the shape of the load-deflection response (post cracking) and available ductility. It should be pointed out that the value of I₅, I₁₀ and I₂₀ is unity for elastic, perfectly brittle material behavior and is equal to 5, 10 and 20 respectively for elastic, perfectly plastic material behavior. Indices higher than those defined above are possible (see Fig. 5.21) depending on the fiber deformation, aspect ratio and volume fraction.

The same variables that affect the ultimate flexural strength of FRC beams also influence the flexural toughness; namely, the type of fiber, volume fraction of fiber, the aspect ratio, the fiber's surface deformation, bond characteristics and orientation.

Ezeldin and Lowe [1991] investigated the flexural toughness for rapid set materials. The primary variables were (a) rapid-set cementing materials, (b) fiber type, and (c) fiber content. Three commercially available rapid-set materials were investigated. Four fiber types made of low-carbon steel were incorporated in the study. Two were hooked at the ends, one was crimped at the ends, and one was crimped throughout the length. Steel fibers were added in quantities of 50, 75 and 100 pcy (30, 45 and 60 kg/m³). The results indicated that steel fibers are very effective in improving the flexural toughness of rapid-set materials. Toughness indexes as high as 4 for 5 and 9 for 10 can be achieved with fiber contents of 75 pcy (45 kg/m³).

Balaguru et al. [1992] studied the flexural behavior of steel fiber reinforced concrete. The focus was on the toughness behavior. The results indicate that fiber content in the range of 50 to 100 lb/yd³ (30 to 60 kg/m³) provide excellent ductility for normal strength concrete. The fiber content has to be increased to about 150 lb/yd³ (90 kg/m³) for high strength concrete. Hooked end fiber geometry provides better results than corrugated and deformed-end geometry. Fiber length, in the range of 1.18 to 2.36 in. (30 to 60 mm.) does not have a significant effect on toughness for hooked-end fibers. Ductile behavior can be obtained using 200 lb/yd³ (120 kg/m³) of fibers, even for concrete containing 20 percent silica fume by weight of cement. It was noted that addition of silica fume improves strength and slightly reduces ductility. The load-deflection behavior of steel fiber reinforced concrete of normal and high strength were earlier shown in Figs. 5.7a and 5.7b. Corresponding to these load-deflection curves, the toughness indexes for hooked end fibers for normal and high strength concretes are shown in Figs. 5.22a and 5.22b. The toughness indexes were calculated based on the ASTM C 1018 procedure. Based on these results the following observations were made: (i) Increase in fiber content results in consistent increase in ductility and energy-absorption capacity. The postpeak load-deflection responses are flatter and the toughness indexes are higher. (ii) Toughness Indexes 5 and 10 computed using the ASTM procedure are not sensitive enough to show the variations that are present in the load-deflection responses. If deflections are measured accurately, values 50 and 100 can be computed for all fiber types and fiber contents greater than or equal to 50 pcy (30 kg/m³). (iii) Higher fiber contents result in much higher load-retaining capacity at large deflections. In almost all cases, there was a considerable difference in 100 between fiber contents. (iv) The magnitude of toughness indexes are quite different from those reported in the literature [Stevens et al. 1995; Balaguru et al. 1992]. (v) Typically, for a given fiber content, toughness indexes are smaller for high-strength concretes compared to normal strength concretes. The differences are less significant at higher fiber volume fractions.

Liang and Galvez [1990] investigated the peak load capacity and toughness of cementitious composite beam specimens reinforced with polyester fibers. A total of more than 50 beam specimens measuring 2 x 2 x 11 in. (50 x 50 x 275 mm) were tested in flexure. Only one fiber diameter (gauge No. 14) with a nominal diameter of 0.078 in. (2 mm) was used. The variables included effect of fiber length, fiber volume fraction and cement matrix mixture on flexural behavior of composites. The fiber length was varied between 1 to 3 in. (25 to 75 mm). The volume fraction of the fibers was varied between 2.5% to 15%. The results indicated that the peak load capacity and toughness of beam specimens were improved with addition of fibers. While the increase of peak load capacity is dependent upon fiber length and fiber volume fraction, the improvement of toughness index shows less sensitivity to these two parameters. The results also indicated that use of water-reducing admixture (RH 1000) apparently reduced the peak-load and toughness of the beam specimens. It was speculated that the addition of RH 1000 in the cement mix may have deteriorated the chemical bonding between the fiber and the matrix.

Tests conducted on steel fiber-reinforced concrete [Otter and Naaman 1988] showed that the increase in toughness was directly related to the volume fraction of fibers with values of toughness index in compression of up to about 4 for specimens reinforced with 2.1 % volume fraction of hooked steel fibers (see Fig. 5.2). For concrete reinforced with straight, smooth fibers, increasing the aspect ratio of fibers from 45 to 80 resulted only in a minimal increase in compressive toughness (see Fig. 5.2b). The use of glass and polypropylene fibers led to low toughness values compared to steel fibers. Otter and Naaman [1988] attributed in part the low performance of glass and polypropylene fibers to the high aspect ratios of the fibers used which led to difficult mixing and possibly higher porosity.

A comprehensive investigation was carried out to study the compression behavior of normal and high strength fiber-reinforced concrete [Ezeldin and Lowe 1991]. The strengths of the concrete were varied from 5 ksi to 12 ksi (35 MPa to 84 MPa). Silica fume was used for high strength concretes. Three fiber volumes and three aspect ratios were considered. The influence of fiber-reinforcing parameters on the peak stress, corresponding strain, the secant modulus of elasticity and the toughness of concrete were investigated. They also showed that increase in silica fume content renders the fiber-reinforced concrete more brittle as compared to concrete without silica fume (Figs. 5.23a and 5.23b). From these figures, it can be seen that the descending portion of the stress-strain curve with 20% silica fume is steeper than those for 0% and 10%. This indicates reduced toughness for high strength concrete.

Taerwe [1992] reported the test results on normal, medium and high strength concrete cylinders under axial compression. The descending part of the stress-strain curve is very steep for the high strength concrete. Adding fibers is shown to have a beneficial effect on the strain-softening behavior and significantly increases toughness, as measured by the area under the stress-strain curve.

Hsu and Hsu [1994] conducted a series of tests on 75 x 150 mm (3 x 6 in.) cylindrical specimens and obtained the complete compressive stress-strain curves for high strength steel fiber-reinforced concrete with and without tie confinement. The volume fractions of steel fibers in concrete were 0, 0.5, 0.75 and 1 percent respectively. Empirical equations were proposed to simulate the stress-strain behavior of high strength steel fiber-reinforced concrete with compressive strengths exceeding 70 MPa (10,000 psi).

The same factors that affect the load-deformation response of fiber-reinforced concrete composites in the postcracking range in flexure tend to affect their behavior in direct tension. In general, increasing the volume fraction and aspect ratio of fibers and enhancing their bond characteristics (hooked and crimped fibers) tend to increase the slope of the postcracking load-deformation response and hence increases the toughness of the fiber composite. The toughness of the fiber composite in direct tension (defined and measured in accordance with ASTM C 1018) can be one or two orders of magnitude higher than that of plain concrete. This is due to the large frictional and fiber-bending energy developed during fiber pullout on either side of the crack and due to larger deformation encountered as a result of multiple cracks (if they occur) in comparison with the single crack that normally develops in plain concrete.

Little information is available on modeling the descending branch of the stress-elongation curve of fiber-reinforced concrete composites (stage III in Fig. 5.12). However, for steel fiber-reinforced concrete in which fiber pullout occurs through a single crack (stage II of Fig. 5.13), prediction equations were proposed by Visalvanich and Naaman [1983], and Nammur and Naaman [1986]. Fibers are also known to increase significantly the strain capacity of concrete composites under compression loads. It can be seen from Figs. 5.1 and 5.2 that increasing the aspect ratio and/or increasing the volume fraction of fibers produces in general a less steep descending portion, which results in a larger area under the stress-strain curve, higher ductility, and higher toughness of the composite compared to that of plain concrete. The improved toughness in compression due to fiber reinforcement is particularly useful in preventing sudden and explosive type of failure under static loading and in absorbing energy under dynamic loading.

Ezeldin and Balaguru [1992] proposed an analytical expression to generate the complete compressive stress-strain curve for fiber-reinforced concrete without silica fume, using the fiber parameter, , and strain corresponding to the compressive strength, of . The proposed analytical expression is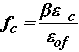

where f_cf is the compressive strength of fiber concrete, of is the strain corresponding to compressive strength, f_c and (_c are the stress and strain values on the curve and is the material parameter. To use the above equation only two values are needed, namely E_of of and . The authors claimed that the above equation provided a good correlation between predicted and experimental results.

Considerable ductility and toughness can be achieved by using SIFCON and SIMCON. Experimentally observed stress-strain behavior of SIFCON in compression in comparison with plain concrete, fiber-reinforced concrete, and mortar is given in Fig. 5.24.

5.2.2.4  Coefficient of Thermal Expansion

The authors are not aware of any investigation dealing with the thermal expansion of fiber-reinforced concrete. Since the coefficient of thermal expansion of steel is of the same order as that of concrete, it is expected that the coefficient of thermal expansion of steel fiber-reinforced concrete will be similar to that of the plain concrete matrix. When other fibers such as polypropylene or glass fibers are used in small volume fractions, the same conclusions can be drawn. However, for large volume fractions of fibers, it would be reasonable to use the simple rule of mixtures, as a first approximation, to determine the coefficient of thermal expansion, provided that the temperature to which the composite is subjected does not affect significantly the properties of the fibers and their interfacial bond with the matrix.

5.2.2.5  Poisson's Ratio

Little information exists on the Poisson's ratio of fiber-reinforced concrete. In most analytical studies, the Poisson's ratio is generally assumed to be the same as that of concrete. This may be a reasonable assumption provided that the composite remains in the elastic range of behavior. As soon as cracking develops, the confining effects of the fibers bridging the cracks will have a significant effect on the lateral deformation, thus the value of the measured Poisson's ratio. At the time of this writing, no investigation is known to have addressed this issue.

5.2.2.6  Fracture Toughness

Cementitious matrices such as mortar and concrete have low tensile strength relative to their compressive strength, and fail in a brittle manner. One way to improve their fracture properties is to reinforce them with randomly distributed fibers. There have been increasing attempts in recent years to characterize cementitious composites (i.e. concrete and fiber-reinforced concrete) by their fracture properties. Both linear-elastic and elastic-plastic fracture mechanics techniques were applied. The crack growth mechanism in these materials is described in terms of three different zones: a stress-free zone, a pseudo-plastic zone, and a process zone [Visalvanich and Naaman 1983]. The stress-free zone is the zone where the fibers have either completely pulled out or failed; the pseudo-plastic zone is the zone where the matrix has cracked but the fibers bridging the crack provide some resistance to pullout; the process zone is the distributed region in front of an advancing crack due to the stress concentration field. The pseudo-plastic zone provides the main contribution to the fracture energy of fiber-reinforced cement composites. Apparent critical fracture energies observed [Visalvanich and Naaman 1983] at stabilization of crack propagation were of the order of 50 lb-in/in² (8,750 J/m2) for fiber-reinforced mortar containing 1% fibers by volume, in comparison to 0.5 lb-in/in² (88 J/m2) for plain mortar. However, the fracture toughness or the critical fracture energy cannot solely characterize fracture of fiber-reinforced concrete. The entire crack growth resistance energy is considered essential because it describes crack initiation, the slow stable crack growth process, and the crack extension prior to rapid propagation and fracture.

The postcracking toughness (measured by means of a toughness index) of high strength concretes with steel and polypropylene fibers increases with increase in volume fraction fibers [Benaiche and Baar 1989]. The fracture toughness of cement-based composites reinforced with relatively high fiber volume (up to 15 percent) was studied by Mobasher et al. [1990b]. Crack propagation and damage distribution were examined by laser holographic interferometry Based on fracture mechanisms observed during experimental studies, a R-curve approach was proposed to predict the toughening of matrices due to fiber reinforcement. The theoretical predictions show a good agreement with the experimental results for both the steel fiber composites and glass fiber composites.

The fracture energy of synthetic FRC depends on the fiber type, volume fraction and fiber lengths, and on the particular fiber finish and pretreatment. Fig. 5.25 shows the range of fracture energy obtained for a variety of synthetic FRCs (fibers used as is from the manufacturer), based on uniaxial tensile tests results by Wang et al. [1990]. The data for concrete cement and high strength aluminum alloy was added by Li et al. [1989] for reference. It is clear that the fracture energy of some synthetic FRC may reach that of certain high strength metallic alloy. Further improvements may be expected when fiber, matrix and interface parameters are optimized for the FRC composites. It appears that the influence of fiber length dominates the composite toughness over other parameters, including the fiber type. The frictional pullout is apparently the most important toughening mechanism.

Further improvements in toughness can be achieved by means of fiber pretreatment to effect local crimp or irregularities or to induce controlled damage of fiber during the pullout process. The success in toughening high strength concrete depends critically on overcoming the issues related to workability with higher fiber volume fractions, compressive strength reduction problems and also on using high performance fibers which have high modulus, high tensile strength and a high bond strength with the matrix.

5.2.2.7  Impact Resistance

Impact resistance is essential for applications such as the bridge piers. It is well recognized that the addition of fibers to concrete enhances the impact resistance. A number of studies have been conducted to develop information on the impact behavior of fiber-reinforced concretes. A summary of the work reported since 1989 is presented below.

Ramakrishnan et al. [1989b] used four types of steel fibers to evaluate the impact resistance. The impact specimens were tested at 28 days by the drop weight test method [ACI Committee 544 1990]. This method is simple, inexpensive and can also be conducted in the field. The impact tests were conducted for hooked-end steel (Type A), straight steel (Type B), corrugated steel (Type C), and polypropylene (Type D) fibers. Type A had an apparent aspect ratio of 100, while Type B had an aspect ratio of only 40. Fig. 5.26 shows the number of blows for first crack and full failure. The maximum increase in impact resistance results from the use of Type A fiber, but Type C fiber also contributes a higher impact resistance at higher fiber contents. The impact strength at first crack increased considerably with the increase in fiber content. Compared with plain concrete, the increase in impact strengths at full failure were 640%, 847%, 1,824% and 2,806% respectively for concretes with 0.5, 1.0, 1.5, and 2.0% (volume) Type C fiber content. The results of the study prove that fiber concretes incorporating hooked-end and corrugated steel fibers (Types A and C) have excellent impact resistance.

The impact resistance for concretes with various volume fractions of fibrillated polypropylene fibers [Alwahab and Soroushian 1987] is shown in Fig. 5. 27. The results indicate that significant improvement in impact resistance of concrete can be achieved with relatively low volume fraction of polypropylene fibers. Bentur [1989] studied the impact resistance of normal and high strength concretes with low volume of friblillated polypropylene fibers. The results indicated that low volume content of polypropylene fiber reinforcement (0.1% to 0.5%) had only a small positive influence on the impact resistance of both normal and high strength concretes.

Bayasi and Celik [1993] reported that polypropylene and polyester fibers enhanced the impact resistance of concrete. Furthermore, adding silica fume at 5 and 10% (mass) increases the impact resistance even more. It is postulated that this increase is attributed to the improvement in fiber dispersion and in bond between fibers and concrete caused by silica fume. Their data indicated that a silica fume content of 5% (mass) is optimal for impact resistance. It can also be postulated that the adverse effects on workability, caused by high contents of silica fume or fibers, resulted in the reduction in the impact resistance of the material.

5.2.3  Fatigue

In many applications, particularly in pavements, bridge deck overlays, and offshore structures, the flexural fatigue strength and endurance limit are important design parameters because these structures must be designed for fatigue load cycles.

No standard test (specimen size, type of loading, loading rate, fatigue failure criteria) is currently available to evaluate the flexural fatigue performance of fiber reinforced concrete. However, several earlier experimental fatigue studies were conducted on steel fiber-reinforced concrete and mortar in bending [Batson et al. 1972; Zollo 1972] using a testing procedure, specimen sizes, and loading conditions similar to those employed for static flexural tests of FRC or tests for conventional concrete with reversed and non-reversed type fatigue loading.

Fatigue strength can be described as the maximum flexural fatigue "stress" at which FRC composites can withstand a prescribed number of fatigue cycles before failure. Alternatively, it could be defined as the maximum number of fatigue cycles needed to fail a beam under a given maximum flexural stress level. However, the fatigue strength is often evaluated on the basis of endurance limit. The endurance limit of FRC in flexural bending is defined as the maximum flexural stress at which the beam could withstand a prescribed number of loading cycles (usually 2 million cycles), expressed as a percentage of either: (1) its virgin static flexural strength (first cracking strength or modulus of rupture), or (2) the maximum static flexural strength of similar plain unreinforced matrix (control). The flexural fatigue strength of steel FRC was reported to be about 80% to 90% of its static flexural strength at 2 million cycles when non-reversed loading is applied and about 70% of its static flexural strength when full reversed loading is used [ACI Committee 544 1990].

In evaluating available fatigue data of steel FRC, Anderson [1978] indicated that past investigations could have probably underestimated the fatigue resistance of steel FRC. This is because those investigations used the first cracking strength of the fiber composite as the reference strength. Since fiber addition modifies the cracking strength of plain concrete, Anderson pointed out that proper reference strength for fatigue evaluation of FRC beams should be taken as the unreinforced plain matrix beam strength. Using the proposed method of fatigue evaluation, Anderson showed that the fatigue resistance based on published fatigue data was much higher than reported. Fatigue tests conducted on steel fiber-reinforced concrete by Ramakrishnan et al. [1987b] showed that the addition of collated hooked-end steel fibers results in a considerable increase in the flexural fatigue strength of concrete. The flexural fatigue strength was increased by 200% to 250%, and endurance limit (to achieve two million cycles) was increased 90% to 95 %, when compared to plain concrete.

From tests of similar beam specimens with dimensions 6 x 6 x 21 in. (150 x 150 x 525 mm) in flexural fatigue under 20Hz non-reversed loading with different types of fibers (hooked, straight, corrugated steel fibers and polypropylene fibers) and different volume fractions of fibers (0.5% and 1.0%), Ramakrishnan et al. [1989b] observed that the fatigue strength and endurance limit (to achieve two million cycles) increased with the addition of fibers and increasing volume fraction of fibers. For instance, expressed as a percentage of modulus of rupture of plain concrete, the endurance limit for mixes with corrugated end fibers was 71% for the 0.5% fiber content and 86% for the mix with 1% fiber content. This represents an increase of 9% and 32% respectively over the endurance limit of 65% observed for plain concrete. Also it was observed that the improved bond characteristics of fibers improves the fatigue strength of fiber composites. The highest increase in fatigue strength was with hooked-end steel fibers and the lowest increase was with straight steel fibers and polypropylene fibers. Ramakrishnan et al. also reported that, if expressed as percentage of its modulus of rupture rather than that of the plain unreinforced matrix, the improvement of endurance limit with increasing volume fraction of fibers is either only slight (hooked-end fibers) or unfavorable for the other types of fibers used (polypropylene). Hence the improvement in the endurance limit is only evident when expressed in relation to the unreinforced matrix. This is in support of the observation made by Anderson [1978].

Johnston and Zemp [1991] investigated flexural fatigue behavior of steel fiber reinforced concrete involving nine different mixtures, including a control concrete without fibers. The fiber parameters were varied such that the effects of fiber content, fiber aspect ratio, and fiber type could be studied independently, while other fiber variables were held constant. The fiber content was varied between 0.5 to 1.5 percent (volume). The fiber's aspect ratio was varied from 47 to 100. The fatigue tests were conducted to a maximum of 500,000 cycles. A total of 194 fatigue tests and 135 tests for static flexural strength were conducted. Comparison of the S-N relationships based on stress as a percentage of first crack strength under static loading shows essentially the same trends as S-N relationships based on stress as a percentage of ultimate strength under static loading. In terms of S-N relationships based on stress percentage of first-crack strength, both fiber and aspect ratio are quite important. Fiber contents in excess of 1.0 percent (volume) are associated with better performance, as are fiber aspect ratios above 70 compared with those around 50. Stiffer high strength wire fibers perform slightly better than ductile low strength slit sheet fibers with aspect ratios over 70, but at aspect ratios around 50, differences in performance by type between smooth wire, surface-deformed wire and melt-extract fibers are small. Endurance limits at 100,000 cycles are 84 to 89 percent of the static first crack strength for the better combinations of fiber parameters, i.e., 1.0 percent volume or more of at least 70 aspect ratio fibers. For less effective combinations with 1.0 percent (volume) or less of fibers having aspect ratios around 50, the 100,000 cycle endurance limit is 75 to 80 percent of the static first crack strength. In terms of actual applied stress versus number of loading cycles, fiber content becomes the primary governing factor, with aspect ratio and fiber type of secondary importance. The best performance, a 100,000 cycle endurance limit of 6.9 MPa (1,000 psi) was obtained with 1.5% by volume of 75 aspect ratio cold-drawn wire fibers in a concrete with a w/(c+f) of 0.49. For 0.5% (volume) of same fibers, the 100,000 cycle endurance limit is only 5.2 MPa (750 psi) despite a lower w/(c+f) of 0.39.

Batson [1991] studied the flexural fatigue of concrete reinforced with three types of metallic and one type of synthetic fiber in volume percentages from 0.1 to 2.0. The beams reinforced with metallic fibers exhibited greater fatigue strength as compared to beams with synthetic fibers. The cyclic load for any one test was fixed percentage of the 28 day static flexural strength, ranging from 95 to 40% depending on the fiber type and fiber volume percentage. The tests were run until 2 million cycles or failure. The fatigue strength increased with fiber volume percentage for each type of fibers. The fatigue strength of beams varied with deformed shape of metallic fibers. The tests by Batson [1991] showed that hooked-end fibers at 1% by volume had superior fatigue strength compared to straight, crimped, and synthetic fibers with even higher volume percentages. Fatigue strength increased with fiber volume percentage and the synthetic fiber had the lowest fatigue strength approaching the value for plain concrete. The hooked-end fiber concrete had the greatest toughness indices and synthetic fiber concrete had greater toughness indices than the straight metallic fiber. He concluded that the durability of concrete reinforced with steel fibers subjected to fatigue loads could be enhanced significantly. Fatigue strengths greater than 80 percent of the 28 day static flexure strength were achieved depending on the type and volume percentage of the fiber. The S-N diagram showing the fatigue performance of Type A (steel fibers with hooked ends) with 1% by volume and 0.5% by volume, respectively, is shown in Figs. 5.28a and 5.28b.

Flexural fatigue strength of fibrillated polypropylene fiber-reinforced concretes was investigated by Nagabhushanam et al. [1989]. Three volume fractions of fibers were used. The test results indicated that the flexural fatigue strength and endurance limit (for 2 million cycles) of concretes with fibers were significantly improved when compared to plain concrete. The static flexural strength increased after being subjected to fatigue loading.

The fatigue characteristics of steel fiber-reinforced concrete under uniaxial and biaxial compressive stresses was studied by Yin and Hsu [1990]. The S-N curves and the cyclic deformations of fiber concrete were compared with those of plain concrete. It was reported that the S-N curve of fiber concrete is a straight line from 1 cycle to 1 million cycles, rather than a curve which can be approximated by two straight lines as in plain concrete (Figs. 5.29a and 5.29b). The addition of fibers to concrete increased the fatigue life as well as ductility, while the failure mode remained the same.

5.2.4  Durability

5.2.4.1  Abrasion Resistance

A review of abrasion studies of hydraulic structures undertaken by ACI Committee 544 [1982, 1988, 1990] has shown that if erosion of the concrete surface is due to a gradual wearing as a result of small particles of debris rolling over the surface at low velocities, then the quality of aggregate and the hardness of the surface determine the rate of erosion. Hence fibers have no effect in this regard. On the other hand, when erosion is due to abrasion resulting from high velocity flow and impact of large debris, steel fiber concretes have provided significant erosion resistance.

Abrasion tests [Nanni 1989] in accordance with ASTM C 799, procedure C, on field-cut and laboratory-made specimens showed no significant difference between the abrasion resistance of plain concrete and steel or synthetic fiber-reinforced concrete. However, the results indicated beneficial effects of steel fibers on scaling prevention of existing pavements [Nanni and Johari 1989]. As pointed out by ACI Committee 544 [1982, 1988, 1990], abrasion as it relates to pavements, and slabs, wear under wheeled traffic is similar to the low velocity erosion in hydraulic structures where the presence of fibers is not expected to increase the abrasion resistance of concrete.

An extensive study was recently completed by Sustersic et al. [1991] in which erosion-abrasion resistance of steel fiber reinforced concrete specimens was investigated according to CRD-C-63-80 test method and abrasion resistance according to Bohme test method. Nine mix proportions were used. The w/c ratios were varied from 0.30 to 0.65. The proportions of hooked steel fibers were varied from 0.25 to 2.0% by volume at w/c of 0.30 and the other w/c ratios, the quantity of the fibers were held constant. For comparison purposes, mixes without fibers were made at each w/c. Results showed that adding steel fibers in concrete improves the resistance as measured by both test methods. The erosion-abrasion resistance is improved by an increase in the compressive strength and by an increase in fiber content. It can be correlated to improvements of abrasion resistance from the Bohme test method but only at constant w/c and different content of fibers.

5.2.4.2  Freezing and Thawing

As pointed out by ACI Committee 544 [1982, 1988, 1990], the addition of fibers themselves has no significant effect on the freezing and thawing resistance of concrete. That is, concretes that are not resistant to freezing and thawing will not have their resistance improved by the addition of fibers [Schupack 1985; Hoff 1987]. Hence, the well-known practices for achieving durable concrete and the same air entrainment criteria for plain concrete should be used also for fiber reinforced concrete.

Notable work prior to 1989, including those of Bedard et al. [1986] and Balaguru and Ramakrishnan [1986], developed the understanding that the addition of entrained air improves the freeze/thaw durability of FRC in a manner similar to that of plain concrete. Based on their experimental results, Balaguru and Ramakrishnan [1986] proposed that for a w/c of more than 0.4 (for most field applications) and cement content less than 700 pcy (415 kg/m³), a minimum of 6% (preferably 8%) entrained air should be used to improve the freeze/thaw resistance of fiber reinforced concrete.

Morgan [1991] summarized the results of several laboratory studies in which both wet and dry-mix fiber reinforced shortcretes were tested according to ASTM procedure A (freezing and thawing in water). It was shown that both steel and high volume polypropylene fiber reinforced wet-mix shortcretes can be made freeze/thaw durable, provided that the shortcrete is properly air entrained. Non-air entrained fiber reinforced wet-mix shortcrete deteriorates very rapidly in the ASTM C666 Procedure A test. It is not currently possible to practically produce high volume polypropylene fiber reinforced shortcrete using the dry-mix process so the inherent freeze/thaw durability of such a system is not known.

Very recently, a study was concluded [Vares 1994], which investigated the influence of Dramix steel fibers on the microstructure of steel fiber-reinforced concrete (SFRC) and the influence of the microstructure on frost resistance. The frost resistance of SFRC with 2% and 4% steel fibers was determined after subjecting the concretes to 100 and 200 freeze/thaw cycles, by comparing changes, toughness and microstructure with those specimens stored in water. No serious damage to SFRC microstructure was observed after 200 freeze/thaw cycles.

5.2.4.3  Wet-Dry Exposure

The effect of addition of polypropylene fiber to concrete mix and adequate curing in enhancing the detoriation resistance of concrete surface skin subjected to cyclic wet/dry seawater exposure was evaluated [Al-Tayyib and Al-Zahrani 1990]. Tests were carried out on 30 concrete slabs specimens of 375 x 750 x 75 mm (15 x 30 x 3 in.), made with and without polypropylene fibers. Some specimens were cured under laboratory-controlled conditions and were subjected to the wet/dry cycles for 85 weeks, while others were cured under field conditions and were subjected to the same cycles for 50 weeks. The results indicate that addition of polypropylene fibers effectively retard the deterioration process of the surface skin of the concrete specimens cured in hot weather environment.

5.2.4.4  Alkaline Environment

The durability of fibers in concrete is a concern for non-metallic fibers. Durability studies were recently conducted for synthetic fibers made of nylon 6, polypropylene and polyester [Khajuria et al. 1991]. Long term durability was estimated using an accelerated aging process. In this process the specimens are stored in lime saturated water maintained at 50oC. The integrity and effectiveness of fibers were studied using flexural toughness of 100 x 100 x 350 mm (4 x 4 x 14 in.) prisms tested under four point loading. Results indicate that, at a fiber content of 4.75 kg/m³ (7.92 pcy), all three types of fibers provide postcracking resistance. Nylon 6 and polypropylene fibers are durable in alkaline environment present in concrete. Specimens with polyester fibers had some loss of ductility when subjected to accelerated aging.

5.2.5  Applications for Pavements

Fiber-reinforced concrete has been used worldwide with and without conventional reinforcement in many field applications. These include bridge deck overlays, floor slabs, pavements and pavement overlays, refractories, hydraulic structures, thin shells, rock slope stabilization, mine tunnel linings and many precast products. The guide for specifying, proportioning, mixing, placing, and finishing steel fiber-reinforced concrete is available from the ACI Committee 544 [1993]. The addition of steel fibers is known to improve most of the mechanical properties of concrete, namely, its static and dynamic tensile strength, energy absorption and toughness and fatigue resistance. Hence proper utilization of steel fiber-reinforced concrete depends on the skill of the engineer in taking advantage of its improved characteristics under a given loading for a given application and the cost effectiveness of the fiber addition.

The use of fiber-reinforced concrete in pavement applications started in the early 1970s. Many actual applications and experimental field studies of fiber concrete pavements and overlays have been reported [ACI Committee 544 1982, 1988, 1993; Hoff 1985; Lankard and Shrader 1983; Schrader 1985; Vandenberghe and Nemegeer 1985] in several countries around the world. These pavement applications included bridge deck overlays, pavements and pavement overlays, airfields, taxiways, aircraft aprons, and industrial floor slabs. The size of applications (overlays and pavements) varied between those of small streets and bridge segments (in residential and rural areas) of 100 ft to 200 ft (30 m to 60 m) long to as large as 570,000 sq. ft (5,300 sq. m) at McCarren International Airport in Las Vegas, Nevada, 315,000 sq. ft (3,000 sq. m) at Norfolk Naval Air Station in Virginia, and about 600,000 sq.ft (5,600 sq.m) at Taoyuan Air Base in Taiwan. As reported by Lankard and Schrader [1983], 22 airport paving projects were completed in the United States as of 1983. Also, over 11 million square feet (one million square meters) of fiber-reinforced concrete slabs were constructed as industrial floors in Europe since 1984 [Vandenberghe and Nemegeer 1985]. Almost all of the fiber-reinforced concrete pavement applications indicated above used steel fibers. Applications in which other commonly known types of fibers such as polypropylene, carbon, or glass fibers or a combination of fibers are almost nonexistent. The amount of steel fiber used in experimental and actual pavement applications (bridge deck overlays, pavements and pavement overlays, airfields) varied from as low as 60 pcy (36 kg/m³) to as high as 265 pcy (157 kg/m³) with an average of about 175 pcy (104 kg/m³). The cementitious content varied between as low as 550 pcy (330 kg/m³) to as high as 970 pcy (575 kg/m³).

Typical material properties of steel fiber-reinforced concrete used for pavements and overlays [ACI Committee 544 1988] are: flexural strength = 900 psi to 1,100 psi (6 MPa to 8 MPa), compressive strength 6,000 psi (42 MPa), Poisson's ratio = 0.2, and modulus of elasticity = 4.0 x 106 psi (28 GPa). Recommended mix proportions for normal weight fiber-reinforced concrete can be found in the report of ACI Committee 544 [1990].

Many of the early experimental and actual fiber-reinforced concrete pavements and overlays developed full-width transverse cracks within 24 to 36 hours after placing [Hoff 1985] and exhibited some degree of curling and corner cracking [Schrader 1984]. The amount of curl is typically 1/8 in. (3 mm) with a range of 0 to 5/8 in. (0 to 16 mm). Corner cracking generally begins to occur after 1 year of service and breaks in an arc of about 1 to 4 ft (0.3 to 1.2 m) radius around the corners where longitudinal and transverse joints meet.

Curling is a common problem of concern in concrete pavements and overlays and does not depend on whether FRC or conventional concrete is used. Although it is difficult to find a common denominator to the degree of curling or cracking, several recommendations have been presented [Lankard 1975; Lankard and Schrader 1983; Schrader 1984] to minimize the level of curling and cracking in FRC pavements and overlays. These include: (1) reducing the cement content and increasing the aggregate content of the concrete, (2) replacing a portion of the cement content with fly ash, (3) using shrinkage compensating concretes, and (4) using water-reducing and set-retarding admixtures.

An experimental rehabilitation project was conducted on the Transcanadian Highway where old concrete pavement was covered with a thin, steel fiber reinforced concrete overlay [Chanvillard et al. 1989]. The surface of the old pavement was either sandblasted or scarified. Three different types of steel fibers were used, and all overlays was bonded with a thin cement grout. In addition, two lanes were repaired with some mechanical bonding provided by a 37.5 mm (1.5 in.) steel nails. In 1989, a thin bonded overlay (TBCO) was used in Japan on a jointed portland cement concrete pavement (PCCP) and continuously reinforced concrete pavement (CRCP) [Ibukiyama et al. 1989].

In Canada, twenty six bridge decks were restored with steel fiber reinforced concrete overlays and structural repairs were made to the beams, piers, or abutments of 19 bridges using steel fiber reinforced concrete, dry-process shortcrete [Johnston and Carter 1989].

Road-work performed along autoroute 40 in the suburbs of Montreal provided an opportunity to monitor the behavior of a thin bonded overlay of fiber-reinforced concrete [Chanvillard and Aitcin 1990]. Examination of the road more than 2 years after it was recommissioned clearly indicated that fibers had a positive effect on the condition of the road.

A demonstration project was built in Rapid City, South Dakota [Ramakrishnan et al. 1991]. The entire project consisted of a pavement that was 740 m (2,428 ft) long and 14.6 m (48 ft) wide. The slab was designed as a 19 cm (7.5 in.) thick plain concrete pavement. Two sections were chosen to study the feasibility of construction and evaluation of fiber reinforced concrete. The first section was 27.5 m (90 ft) long and 15 cm (6 in.) thick. The second section was 23 m (75 ft) long and 12.5 cm (5 in.) thick. Transverse and longitudinal joints were placed at 4.5 m (15 ft) and 3.6 m (12 ft) respectively. The experience indicates that, if proper care is taken, results obtained in the laboratory can be reproduced in the field without any problems.

5.3  Continuous Fiber-Reinforced Concrete

In the last 5 years, there has been significant interest and development in the use of continuous fiber reinforcement for improving the behavior of cementitious composites and/or concrete. Fiber Reinforced Polymers (FRP) or sometime also referred to Fiber Reinforced Plastic are increasingly being accepted as an alternative for uncoated and epoxy-coated steel reinforcement for prestressed and non-prestressed concrete applications.

In 1990, the American Concrete Institute formed the ACI Committee 440 on Non-Metallic Reinforcement. The Committee has just developed a state-of-the-art report on Fiber Reinforced Plastic (FRP) for Concrete Structures [ACI Committee 440 1996].

In 1992, the first international conference was held in Montreal, Canada [Neale and Labossiere 1992]. This was followed by an international conference in Ghent, Belgium [Taerwe 1995]. A specialty conference with emphasis on use of FRP for bridges was held in Canada [Mufti 1991]. Recently, another international conference was held in Montreal, Canada [El-Badry 1996].

This section describes the FRP materials and their engineering properties. The applications in the transportation systems of structural concrete reinforced and/or prestressed with FRP materials are also summarized.

5.3.1  Constituent Materials

Concrete reinforced with continuous fibers rather than short discrete fibers is also termed as Fiber-Reinforced Composites. In general terms, Fiber-Reinforced Composites are a materials system. The term "composite" can be applied to any combination of two or more separate materials having an identifiable interface between them, most often with an interphase region such as a surface treatment used on selected constituents to improve adhesion of that component to the polymer matrix. Composites are defined as a matrix of polymeric material reinforced by fibers or other reinforcement with a discernible aspect ratio of length to thickness.

5.3.1.1  Reinforcing Fibers

The principal fibers in common commercial use for civil engineering applications include glass, carbon and aramid. The most common form of fiber-reinforced composites used in structural applications is called a laminate. Laminates are made by stacking a number of thin layers (laminae) or fibers and matrix and consolidating them into the desired thickness. Fiber orientation in each layer as well as the stacking sequence of the various layers can be controlled to generate a wide range of physical and mechanical properties for the composite laminate.

A composite can be any combination of two or more materials so long as the material properties of different and there is a recognizable region for each material. The materials are intermingled. There is an interface between the materials, and often an interphase region such as the surface treatment used on fibers to improve matrix adhesion and other performance parameters via the coupling agent.

The performance of the composite depends upon the materials of which the composite is manufactured, the arrangement of the primary load-bearing reinforcing fiber portion of the composite and the interaction between these materials. The major factors affecting the performance of the fiber matrix composite are: fiber orientation, length, shape and composition of the fibers, the mechanical properties of the resin matrix and the adhesion or bond between the fibers and the matrix.

Glass has been the predominant fiber for many civil engineering applications because of an economical balance of cost and specific strength properties. Glass fibers are commercially available in "E-Glass" formulation (for "Electrical" grade), the most widely used general-purpose form of composite reinforcement, high strength S-2 glass and ECR Glass, a modified E-Glass which offers greater alkali resistance. Although considerably more expensive than glass, other fibers including carbon and aramid are used for their strength or modulus properties or in special situations as hybrids with glass.

There are three sources for commercial carbon fibers: pitch (a by-product of petroleum distillation), PAN (polyacrylonitrile) and rayon. The properties of carbon fiber are controlled by its molecular structure, and degree of freedom from defects. The formulation of carbon fibers requires processing temperatures above 1000C. At this temperature, most synthetic fibers will melt and vaporize; however acrylic does not and its molecular structure is retained during high temperature carbonization.

There are two types of carbon fiber — the high modulus type, Type I, and the high strength type, Type II. The difference in properties between Types I and II is a result of the differences in the fiber microstructure. These properties are derived from the arrangement of the graphene (hexagonal) layer networks present in graphite. If these layers are present in three-dimensional stacks, the material is defined as graphite. If the bonding between layers is weak and two dimensional layers occur, the resulting material is termed as carbon.

5.3.1.2  Polymer Resins

Unsaturated polyester (UP) is the polymer resin most universally used to produce large composites for structural applications. The Composites Institute estimates that approximately 85% of U.S. composites production is based on unsaturated polyester resins. As mentioned earlier, these resins are typically in the form of low viscosity liquids during processing or until cured. However, partially processed materials containing fibers can also be used under specific conditions of temperature, and pressure. This class of materials has its own terminology, with the most common pre-production forms of partially reacted or chemically-thickened materials being prepreg (pre-impregnation) and sheet molding compounds (SMC).

Unsaturated polyesters are produced by reacting a di-basic acid containing maleic anhydride, or fumaric acid. The resulting polymer is then dissolved in a reactive vinyl monomer such as styrene. The viscosity of the solutions will depend on the ingredients, but typically range between 200 to 2,000 centipoises. Addition of heat and/or free-radical initiator such as an organic peroxide causes a chemical reaction which results in non-reversible cross-linking between the unsaturated polyester polymer and the monomer. Room temperature cross-linking may also be accomplished by using peroxides and suitable additives (typically promoters).

5.3.2  Physical and Mechanical Properties

The physical and mechanical properties are obtained by tests on either Fiber Reinforced Polymers (FRP) bars or tendons. It should be recognized that FRP bar is anisotropic, with the longitudinal axis being the strong axis. Second, unlike steel, the mechanical properties of FRPs vary significantly from one product to another. Factors such as volume and type of fiber and resin, fiber orientation, and quality control during the manufacturing, play a major role in establishing the characteristics of the product. Furthermore, the mechanical properties of FRPs, like all composites, are affected by such factors as the loading history and duration, temperature, and moisture.

5.3.2.1  Specific Gravity

FRP bars and tendons have a specific gravity ranging from 1.5 to 2.0; i.e. they are nearly 1/4 of the weight of steel. The reduced weight of the materials leads to lower transportation and storage costs and less handling on the job site and reduced installation time as compared to steel rebars. This is a major advantage which must be included in any cost analysis for product selection.

5.3.2.2  Thermal Expansion

Reinforced concrete itself is a composite material, where the reinforcement acts as the strengthening fiber and the concrete as the matrix. It is therefore imperative that the behavior under thermal stresses for the two materials be similar so that the differential deformations of concrete and the reinforcement are minimized. Depending on the mix proportions, the linear coefficient of thermal expansion for concrete varies from 6 to 12 x 10-6 per oC [Mindess and Young 1981].

5.3.2.3  Tensile Strength

FRP bars and tendons reach their ultimate tensile strength without exhibiting any yielding of the material. The mechanical properties of FRP reported in Table 5.2 were measured in the longitudinal (i.e. strong) direction. It is noted, however, that the values reported for FRP materials cover the range for some of the more commonly available materials. The exact product properties must be obtained from the manufacturer.

5.3.2.4  Tensile Modulus of Elasticity

The longitudinal modulus of elasticity of GFRP bars is approximately 25 percent of that of steel. The modulus for CFRP tendons, which usually employ stiffer fibers, is slightly higher than that for GFRP rebars.

5.3.2.5  Compressive Strength

FRP bars are weaker in compression than in tension. However, the compressive strength of GFRP is not a primary concern for most applications. The compressive strength also depends on whether the rebar is smooth or ribbed. Compressive strength in the range of 317 to 470 MPa (46 to 68 ksi) has been reported for rebars having a tensile strength in the range of 552 to 896 MPa (80 to 130 ksi) [Wu et al. 1991]. Higher compressive strengths are expected for bars with higher tensile strength.

5.3.2.6  Compressive Modulus of Elasticity

Unlike the tensile stiffness, the compressive stiffness of GFRP bars varies with rebar size, type, quality control in manufacturing and the length to diameter ratio of the specimens. The compressive stiffness for GFRP rebars is smaller than the tensile modulus of elasticity. Based on tests of samples containing 55% to 60% volume fraction of continuous E-glass fibers in a matrix of vinylester or isophthalic resin, a modulus of 34 GPa (5,000 to 7,000 ksi) has been reported [Wu et al. 1991]. Another manufacturer reports the compressive modulus at 34 GPa (5,000 ksi) which is approximately 77% of the tensile modulus for the same product [Bedard 1992].

5.3.2.7  Shear Strength

The shear strength of composites is, in general, very low. GFRP bars, for example, can be cut very easily in the direction perpendicular to the longitudinal axis with ordinary saws. This shortcoming can be overcome in most cases by orienting the rebars such that they will resist the applied loads through axial tension.

5.3.2.8  Creep and Creep Rupture

Fibers such as graphite and glass have excellent resistance to creep, while the same is not true for most resins. Therefore, the orientation and volume of fibers have a significant influence on the creep performance of rebars/tendons. One study reports that for a high quality GFRP rebar, the additional strains caused by creep were estimated to be only 3% of the initial elastic strains [Iyer and Anigol 1991].

Under adverse loading and environmental conditions, FRP rebars subjected to the action of a constant load may suddenly fail after a time, referred to as the endurance time. This phenomenon, known as creep rupture, exists for all structural materials including steel. However, for steel prestressing strands, this is not of concern. Steel can endure the typical tensile loads, which are about 75% of the ultimate strength, indefinitely without any loss of strength or fracture. As the ratio of the sustained tensile force to the short-term strength of the FRP increases, the endurance time decreases. Creep tests were conducted in Germany on GFRP composites with various cross sections. These studies indicate that stress rupture diminishes if the sustained loads are limited to 60% of the short-term strength of the sample [Budelmann and Rostasy 1993].

5.3.2.9  Fatigue

CFRP and GFRP bars exhibit good fatigue resistance. Most of the research in this regard has been on high-performance fibers, such as graphite, which are subjected to large cycles of loading in aerospace applications. In tests where the loading was repeated for 10 million cycles, it was concluded that graphite-epoxy composites have better fatigue strength than steel, while the fatigue strength of glass composites is lower than steel [Scwartz, 1992]. In another investigation, GFRP rods constructed for prestressing applications were subjected to repeated cyclic loading with a maximum stress of 72 ksi and a stress range of 50 ksi. The rods could stand more than 4 million cycles of loading before the failure initiated at their anchorage zone [Franke 1981].

5.3.2.10  Durability

In general, FRP materials exhibit excellent durability. Some studies have shown, however, that certain glass and aramid fibers deteriorate when subjected to an alkaline environments, such as that found in concrete. Sen et al. [1993] found that S-2 glass fibers used in prestressed beams showed a rapid and substantial loss in load carrying capacity when exposed to a 15% salt solution. Research by GangaRao et al. [1995]indicated that depending on the resin, strength losses by as much as 64% and stiffness losses up to 9% were found for glass fiber composites that were placed in an alkaline environment. Common aramid fibers can be degraded by strong acids and bases [ACI 440 1996]. Relaxation of Arapree composites were found to be about 40% higher in an alkaline environment at room temperature than in air [Gerritse and Den Uijl 1995]. These fibers are also subject to degradation when exposed to UV rays present in sunlight. This problem can be overcome by embedding the aramid in concrete or by using specially formulated resins. Though the aramid fibers have shown some deterioration, aramid composites have not shown any strength loss. Carbon fibers have been found to be resistant to most chemicals and exhibit excellent durability characteristics.

Matrix materials that resist moisture infiltration or diffusion of hydroxyl ions can help protect fibers against harsh environments. Research by GangaRao et al. [1995] found that the composite resins play a significant role in the durability of glass composite rods. Frequently, durability problems of composite are the result of the properties of the matrix. Moisture absorption in the matrix can result in swelling of the matrix and loss of strength and stiffness of the composite. Fire and high temperature are also a problem more severe for the matrix than the fibers.

5.3.3  Field Applications

Composite materials have been used in a variety of civil engineering applications with both reinforced and prestressed concrete. They are manufactured as reinforcing elements, as prestressing and post-tensioning tendons and rods, and as strengthening materials for rehabilitation of existing structures. Several new structures utilizing FRP reinforcement are currently underway by the West Virginia Department of Transportation and by the Florida Department of Transportation. One such application is a 52 m (170 ft) three-span continuous bridge deck reinforced with FRP reinforcing bars. This chapter describes FRP applications in concrete reinforcement. The projects are grouped under the method of application, either as reinforced concrete, prestressed concrete, or external reinforcement.

5.3.3.1  Applications in North America

• A. Bridge in Calgary, Canada
  A concrete highway bridge was constructed using carbon fiber composite cables (CFCC) and LeadlineR tendons. The bridge is a two-span continuous skew (33.3o) bridge with spans of 22.83 and 19.23 m (75 and 63 ft). Thirteen precast prestressed concrete girders of bulb-tee section were used for each span. The girders are 1.1 m (43 in.) deep and have a 160 mm (6 in.) web thickness. Of the 26 girders, four (two in each span) were prestressed using CFCC cables of 15.2 mm (0.6 in.) in diameter. Two additional girders (one in each span) were prestressed by 8 mm (0.3 in.) diameter LeadlineR rods. These six girders were located at the center of the bridge. The remaining girders were prestressed with steel strands. This bridge is monitored by an optical fiber system consisting of intra-core Bragg grating optic fiber sensors and electric strain gauges attached to CFCC, LeadlineR rods, and steel strands [Rizkalla and Tadros 1994].
• B. Bridge in Rapid City, South Dakota
  A precast post-tensioned bridge of 9 m (30 ft) span and 5.2 m (17 ft) width was erected at a cement plant in 1992 [Iyer and Anigol 1991]. It has a 180 mm (7 in) thick deck slab supported by three longitudinal girders. Cables of three different materials were used to prestress the slab. Thirty GFRP cables were used to prestress one-third of the length of the slab, thirty CFRP cables were used to prestress the next third of the length, and steel cable prestressing was adopted for the remaining length. Each GFRP and CFRP cable consists of seven 4-mm (0.156 in) diameter rods. The initial prestress and final prestress after all losses were set at 0.6Pu and 0.5Pu respectively. Plastic ducts housing the cables were grouted with high-strength epoxy and mortar for bonding purposes, and the temporary anchorages were removed. Monitoring of bridge deflections and stresses in cables and concrete was carried out to assess losses in the cables and the actual deflections under moving loads.
• C. Waterfront Structure in Port Hueneme, California
  This waterfront structure, constructed in 1994, consists of two full-scale bays; one is a prestressed deck with graphite cables, and the other is a fiberglass composite deck. The bays are supported by twelve 356 x 356 mm (14 x 14 in.) piles, 13.7 m (45 ft) long, and reinforced with six prestressed CFRP cables and CFRP spirals. The pile caps were post-tensioned with GFRP (E-glass) cables. The deck was designed for 1,000 kN (225 kips) applied on a 762 mm (30 in.) square area and tested at service load conditions. A total of 180 CFRP cables were used to prestress the 6 m (20 ft) long deck, which has a 5.5 m (18 ft) width and a 457 mm (18 in) thickness.
• D. Column Wrapping Projects in California
  As a part of its general seismic upgrading program, the California Department of Transportation (Caltrans) placed confining jackets around bridge columns using fiberglass mat. Epoxy was used to provide the lap bond splices for the fiberglass mats. Expansive grout was injected beneath the mat to ensure contact with the original concrete. Eleven 1.8 m (6 ft) diameter and four 1.2 m (4 ft) diameter columns were wrapped. These columns, which are located 32 km (20 mi) from Northridge, suffered no damage in the January 17, 1994 earthquake. This wrapping technique has been used on other projects in California. For example, the cities of Los Angeles and Santa Monica used composite wrapping materials on approximately 200 columns in 1993 and 1994.
• E. Column Wrapping Projects in Reno, Nevada
  In 1993, the Nevada Department of Transportation wrapped ninety-six 0.3m (1 ft) diameter columns with a proprietary FRP wrapping system. The columns were part of an interstate highway bridge constructed over a casino, with 48 of those columns actually located within the casino. No odor was detected from the TYFOR S epoxy.
• F. Foulk Road Bridge in Wilmington, Delaware
  Carbon fiber Forca^R tow sheets were used on this 16.5 m (54ft) long, simple-span, prestressed, precast box beam structure that exhibited cracking indicative of the lack of transverse reinforcement. The bridge's superstructure was composed of 24 prestressed box beams placed adjacent to each other. For demonstration purposes, six of the beams were retrofitted. The design of the rehabilitation replicated the strength that 12.5 mm (0.5 in) diameter steel bars would have provided had they been installed in the original casting of the beams. One ply of unidirectional CFRP sheet, with the fibers running transverse to the beam, was used on four beams. Two other beams used a higher modulus, higher weight fabric, with one of those beams fitted with two plies rather than a single ply.

5.3.3.2  Applications in Europe

• A. Marienfelde Bridge in Germany
  A pedestrian bridge in a Berlin park was constructed in 1988 using external prestressing. The superstructure is a two-span double-T beam slab partially prestressed by seven FRP tendons. Spans are 27.6 and 22.9 m (90 and 75 ft). The double-T beam is 5 m (16.5 ft) wide and 1.1 m (3.6 ft) deep.
• B. Ludwigshafen Bridge in Germany
  CFCC strands developed in Japan were used as part of the tensioning materials for a prestressed concrete bridge near a chemical plant. The bridge, which crosses a number of railway tracks, carries heavy truck traffic and was designed to a German road bridge specification requiring a 600/300 kN (135/67.5 kip) load rating. The two-lane bridge has a total length of 85 m (280 ft), and consists of four equal spans: two straight spans and two curved spans with a radius of 62.8 m (206 ft). The superstructure is modeled as a slab-and-beam bridge with a total width of 11.2 m (36.8 ft), and a height of 1.12 m (3.7 ft).
• C. Lunen'sche-Gasse Bridge in Germany
  Polystal^R GFRP tendons were used in 1980 in a 6.55 m (21.5 ft) single-span slab bridge. One hundred GFRP rods 7.5 mm (0.3 in) in diameter were grouped in unbonded prestressing tendons with a length of 7 m (23 ft). Four different anchorage systems were tested. Monitoring of the tensile forces, carried out over a period of 5 years on the grouted anchorage, demonstrated satisfactory performance.
• D. Ulenberg-Strasse Bridge in Germany
  This post-tensioned bridge was erected in 1986 with a total of 59 multi-cables, each consisting of nineteen 7.5 mm (0.3 in.) diameter PolystalR GFRP rods. The allowable tensile force of the cables under service loads was set at 0.47Pu. Cables were anchored with a mortar made of silica sand and polyester resin. Synthetic resin mortar was injected as a grout to overcome the weakness of glass fiber to alkali attack. Similar to the "Lunen'sche-Gasse" bridge, E-glass fibers in a polyester resin matrix with external coating of polyamide were used. The slab bridge was designed for the German 600/300 kN (135/67.5 kip) load class, and has two spans which are 21.3 m (70 ft) and 25.6 m (84 ft) long.
• E. Schiessbergstrasse Bridge in Germany
  This post-tensioned road bridge, designed for the German 600/300 kN (135/67.5 kip) load class, was built in 1990. This is a two-lane triple-span bridge with spans of 16.3, 20.4 and 16.3 m, (53.5, 67 and 53.5 ft). The slab width is 9.70 m (32 ft) and its thickness is 1.12 m (3.7 ft). A total of 27 FRP tendons were used. The bridge has a sophisticated permanent monitoring system with the possibility of on-line diagnostics.
• F. Notsch Bridge in Austria
  This post-tensioned bridge, which has PolystalR GFRP prestressing tendons, was built in 1991. It is a two-lane three-span bridge, with spans of 13, 18, and 13 m (42.7, 59, and 42.7 ft). The slab width is 12 m (39.4 ft), and its thickness is 0.65 m (2.1 ft). It has a permanent monitoring system similar to that on the Schiessbergstrasse bridge.
• G. Ibach Bridge in Switzerland
  Accidental damage to a prestressing tendon during maintenance work necessitated repair of this bridge in 1991. Three 5 m (16.5 ft) long CFRP laminates, two with 150 x 1.75 mm (6 x 0.07 in.) cross sections and one with a 150 x 2.0 mm (6 x 0.08 in.) cross section were applied to the bottom surface of the bridge.

5.3.3.3  Applications in the Japan

• A. Hakui Cycling Road Bridge
  Erected in 1991, this pretensioned hollow slab system utilizes CFCC strands as tendons [Minosaku 1991]. In addition to the prestressing tendons, straight CFRP wires are used as substitutes for diagonal tension reinforcing bars in one-half of the outside girders.
• B. Tabras Golf Club Bridge
  Braided AFRP (FiBRA^R) rods of 14 mm (0.55 in) diameter were used in three of the 21 girders for this slab bridge constructed in 1990 [Tamura and Tezuka 1990]. The bridge is 2.40 m (7.9 ft) wide, with three 11.98 m (39.3 ft) spans, and conforms to the Japan Institute of Standards (JIS) specifications. The allowable tensile force in the AFRP rods was set at 0.5P_u
• C. Takahiko Floating Bridge
  Completed in 1992, this bridge was partially prestressed using 13 and 15 mm (1.0 and 1.2 in) diameter FiBRA^R rods.
• D. South Yard Country Club Suspension Bridge
  Constructed in 1990, this bridge was post-tensioned with 4.86 x 19.5 mm (0.2 x 0.75 in.) flat AFRP (Arapree^R) strips. The anchorage for the post-tensioning was provided by using mortar-filled sleeves.
• E. Iwafune Golf Club Cable-Stayed Bridge
  Constructed in 1992, this bridge was partially prestressed using GFRP and CFRP rods. Anchorage was provided by resin-filled sleeves. The initial prestressing was 0.3P_u
• F. Tsukude Golf Country Club Bridge
  Constructed in 1993, this cantilevered-type pedestrian bridge has a single span of 99.0 m (325 ft) and a width of 3.6 m (12 ft). The main girders were post-tensioned with 12.5 mm (0.5 in.) diameter CFCC rods. The bridge was designed based on the Japan Road Association (JRA) specification for highway bridges.
• G. Nakatsugawa Pedestrian Overbridge
  CFCC strands were used in this pre-tensioned simple slab bridge built in 1989. The bridge was prefabricated in a single piece, and has a width of 2.5 m (8.2 ft) and a length of 8.0 m (26.2 ft). The anchorages used in fabrication were made of threaded steel pipes, with CFCC tendon ends inserted into the pipes and epoxy-injected. The allowable tensile forces were 0.60P_u during prestressing, 0.55Pu immediately after prestressing, and 0.50P_u under service loads. This bridge was fabricated as a nonmetallic structure, and CFRP reinforcing bars with surface ribs and lugs to improve the bond with concrete were used as stirrups and temperature reinforcement.
• H. Birdie Bridge
  This was a post-tensioned suspended slab bridge 2.1 m (6.9 ft) wide and 54.5 m (179 ft) long. Eight AFRP tapes, each with a 4.86 x 19.5 mm (0.2 x 0.75 in.) cross section, were bundled to make a single cable. A total of 16 cables were used, with allowable tensile forces for the cables set at 0.5P_u under initial force, and 0.33Pu under service load. The cables were anchored by a sleeve filled with an expansive mortar. AFRP tapes were also used as non-prestressed reinforcement in the slab. For ground anchors, cables consisting of nine 8 mm (0.3 in.) diameter CFRP rods were used.
• I. Shinmiya Bridge
  This was the first application where carbon fiber composite cable (CFCC) strands were used as tensioning materials for a prestressed concrete bridge, constructed in October 1988 on a national highway. The span and width of the bridge are 5.76 and 7.0 m (19 and 23 ft), respectively. Seven-wire 12.5 mm (0.5 in.) diameter CFCC strands were arranged into six tendons at the bottom flange and two tendons at the top flange. Allowable tensile forces were 0.60P_u during prestressing, 0.53P_u immediately after prestressing, and 0.45P_u under service loads. Epoxy-coated steel reinforcing bars were used for stirrups.
• J. Bachigawa Minamibashi Bridge
  This 18.6 m (61 ft) single-span bridge was constructed in 1989. The design conformed to the JRA specification for highway bridges. The post-tensioning for the precast hollow girder used Leadline^R CFRP cable.
• K. Sumitomo Bridge
  A road bridge, erected at the freight entrance to a concrete products plant, was reinforced with pultruded AFRP rods [Mizutani et al. 1991]. This was a prestressed concrete road bridge consisting of a 12.5 m (41 ft) span pre-tensioned composite slab, and a 25.0 m (82 ft) span post-tensioned box girder. AFRP rods were used for all tendons in both spans. The pretensioned composite slab used AFRP as stirrups and reinforcing bars. AFRP cables consisted of three twisted strands for the pretensioned composite slab, and 19 and seven twisted strands, respectively, for the internal and external cables of the post-tensioned box girder. The allowable tensile forces were 0.8P_u during prestressing, 0.7P_u immediately after prestressing, and 0.6P_u under service loads.
• L. Kitakyushu Bridge
  The width of this bridge is 12.3 m (40 ft) and the total length is 35.8 m (117.5 ft), with one span a 18.25 m (60 ft) pre-tensioned girder and the other span a 17.55 m (57.5 ft) post-tensioned girder. The tendons used were multi-cable bundles of eight 8 mm (0.3 in.) diameter CFRP rods. Eight multi-cables in all were used. The allowable tensile force under service loads was set at 0.55P_u. Anchoring of the cables was achieved with a steel wedge-type anchor, with field monitoring in progress. The tensioning operation was conducted in three stages to reduce the difference in tensioning force between cables.
• M. Maglev Guideway
  The precast side wall beams of this guideway are simply supported girders partially prestressed with 12.5 mm (0.5 in.) diameter CFCC strands. The non-magnetic property of FRP materials was well utilized here. The FRP strand is twisted seven-wire impregnated in epoxy resin. Anchoring was obtained by direct bonding to concrete.
• N. Kuzuha Quay Landing Pier
  This structure was built in 1993 based on Japan's harbor structures design standards. Both pre-tensioning and post-tensioning tendons were CFCC strands of 12.5 mm (0.5 in.) diameter. End anchorage was obtained by direct bonding to concrete and by metal die-cast wedges.
• O. Airport Pavement
  The non-magnetic test pavement at Haneda International Airport has concrete pavement post-tensioned with CFRP and AFRP bonded tendons. The anchorage for post-tensioning was obtained using resin casting and wedges, and was not required to hold the permanent load.
• P. Wrapping Projects
  Forca^RM tow sheet has been used extensively in Japan in over 200 projects including tunnels, chimneys, side walls, and slabs.

5.4  References

• ACI Committee 440. 1996. State-of-the-Art Report on Fiber Reinforced Plastic (FRP) for Concrete Structures (ACI 440R). ACI Manual of Concrete Practice, Part 5, American Concrete Institute, Detroit, MI, 68 pp.
• ACI Committee 544. 1982. State-of-the-Art Report on Fiber Reinforced Concrete (ACI 544.1R-82). Concrete International, May, Vol. 4, No. 5, pp. 9-30.
• ACI Committee 544. 1988. Design Considerations for Steel Fiber Reinforced Concrete(ACI 544.4R-88). Manual of Concrete Practice, Part 5, American Concrete Institute, Detroit, MI, 18 pp.
• ACI Committee 544. 1990. State-of-the-Art Report on Fiber Reinforced Concrete. ACI Manual of Concrete Practice, Part 5, American Concrete Institute, Detroit, MI, 22 pp.
• ACI Committee 544. 1993. Guide for Specifying, Proportioning, Mixing, Placing, and Finishing Steel Fiber Reinforced Concrete. ACI Materials Journal, Jan-Feb, Vol. 90, No. 1, pp. 94-101.
• A. H. J. Al-Tayyib and M. M. Al-Zahrani. 1990. Use of Polypropylene Fibers to Enhance Deterioration Resistance of Concrete Surface Skin Subjected to Cyclic wet/Dry Sea Water Exposure. ACI Materials Journal, Jul-Aug, Vol. 87, No.4, pp. 363-370.
• T. Alwahab and P. Soroushian. 1987. Characterization of Fiber Force Collated Fibrillated Polypropylene Fibers and Their Application to Concrete. Research Report, Department of Civil and Environmental engineering, Michigan State University, 60 pp.
• W. E. Anderson. 1978. Proposed Testing of Steel-Fibre Concrete to Minimize Unexpected Service Failures. Testing and Test Methods of Fibre Cement Composites. RILEM Symposium, The Construction Press, Lancaster, England, pp. 223-232.
• S. A. Ashour and F. F. Wafa. 1993. Flexural Behavior of High Strength Fiber Reinforced Concrete Beams. ACI Structural Journal, May-Jun, Vol. 90, No. 3, pp. 279-287.
• P. N. Balaguru. 1992. Fiber-Reinforced Rapid Setting Concrete. Concrete International, Feb, pp. 64-67.
• P. N. Balaguru, R. Narahari, and M. Patel. 1992. Flexural Toughness of Steel Fiber Reinforced Concrete. ACI Materials Journal, Nov-Dec, Vol. 89, No. 6, pp. 541-546.
• P. N. Balaguru and V. Ramakrishnan. 1986. Freeze-Thaw Durability of Fiber Reinforced Concrete. ACI Journal, May-Jun, Vol. 33, No. 3, pp. 374-382.
• P. N. Balaguru and V. Ramakrishnan. 1988. Properties of Fiber Reinforced Concrete: Workability, Behavior Under Long-Term Loading, Air-Void Characteristics. ACI Materials Journal, May-Jun, Vol. 85, No. 3, pp. 189-196.
• P. N. Balaguru and S. P. Shah. 1992. Fiber Reinforced Cement Composites. McGraw-Hill, New York, 1992, xii, 530 pp.
• N. Banthia and C. Foy. 1989. Marine Curing of Steel Fiber Composites. Journal of Materials in Civil Engineering, May, Vol. 1, No. 2, pp. 86-96.
• B. Barr. 1987. Fracture Characteristics of FRC Materials in Shear. Fiber Reinforced Concrete Properties and Applications. American Concrete Institute, Detroit, MI, pp. 27-53. (ACI SP-105)
• G. B. Batson. 1991. Fatigue Strength Toughness Indices of Fiber Reinforced Concrete. Durability of Concrete. Second International Conference, held in Montreal, Canada; Ed. by V.M. Malhotra; American Concrete Institute, Detroit, MI, Vol. 2, pp. 715-728. (ACI SP-126)
• G. Batson, C. Ball, L. Bailey, and J. Hooks. 1972. Flexural Fatigue Strength of Steel Fiber Reinforced Concrete. ACI Journal, Nov, Vol. 69, No. 11, pp. 673-677.
• Z. Bayasi and T. Celik. 1993. Application of Silica Fume in Synthetic Fiber-Reinforced Concrete. Transportation Research Record, No. 1382, pp. 89-98.
• Z. Bayasi and J. Zeng. 1993. Properties of Polypropylene Fiber Reinforced Concrete. ACI Materials Journal, Nov-Dec, Vol. 90, No. 6, pp. 605-610.
• C. Bedard. 1992. Composite Reinforcing Bars: Assessing Their Use in Construction. Concrete International, Jan, pp. 55-59.
• C. Bedard, G. C. Carette, and V. M. Malhotra. 1986. Development of Air-Entrained, High Strength Concrete: Mechanics Properties and Resistance to Freezing and Thawing. CSCE/CANMET International Workshop on Concrete for Offshore Structures, held on Sept. 10-11, 1986, St. John's, Newfoundland, Canada, 23 pp.
• F. Benaiche and B. Barr. 1989. Fracture Characteristics of High Strength Concrete and FRC materials. Fiber Reinforced Cements and Concretes: Recent Developments. International Conference, held on Sept. 18-20, 1989, University of Wales College of Candift, U.K.; Ed. by R.N. Swamy and B. Barr, Elsevier Applied Science, London, pp. 611-619.
• A. Bentur. 1989. Silica Fume Treatments as Means for Improving Durability of Glass Fiber Reinforced Cements. Journal of Materials in Civil Engineering, Aug, Vol. 1, No. 3, pp. 167-183.
• S. G. Bergstorm. 1976. A Nordic Research Project on Fibre Reinforced, Cement Based Materials. Proceedings of RILEM Symposium on Fibre Reinforced Cement and Concrete, held September 1975, The Construction Press, Lancaster, England, Vol. 2, pp. 595-600.
• H. Budelmann and F.S. Rostasy. 1993. Creep Rupture Behavior of FRP Elements for Prestressed Concrete - Phenomenon, Results and Forecast Models. Proceedings of ACI International Symposium on FRP Reinforcement for Concrete Structures, held March 1993, Vancouver, B.C., Canada, pp. 87-100.
• G. Chanvillard, P-C. Aitcin, and C. Lupien. 1989. Field Evaluation of Steel Fiber Reinforced Concrete Overlay With Various Bonding Mechanisms. Transportation Research Record, No. 1226, pp. 48-56.
• G. Chanvillard and P-C. Aitcin. 1990. Thin Bonded Overlays of Fiber Reinforced Concrete as a Method of Rehabilitation of Concrete Roads. Canadian Journal of Civil Engineering, Aug, Vol. 17, No.4, pp. 521-527.
• Concrete and Aggregates. 1988. Annual Book of ASTM Standards, Part 04.02, ASTM, Philadephia, PA, 751 pp.
• Concrete Toughens Up. 1991. Materials Engineering, Jan, Vol. 102, p. 38.
• N. J. Dave. 1991. Fatigue Performance of Fibre-Reinforced Cement Composite Concrete Beams. Durability of Concrete, Second International Conference, 1991, Montreal, Canada; Ed. by V. M. Malhotra; American Concrete Institute, Detroit, MI, Vol. 2, pp. 697-713. (ACI SP-126)
• J. Edington, D. J. Hannant, and R. I. T. Williams. 1974. Steel Fiber Reinforced Concrete. Paper No. CP 69174, Building Research Establishment, Garston, Waterford, England, 17 pp.
• M. El-Badry (Ed.). 1996. Proceedings of the 2nd International Conference — Advanced Composite Materials in Bridges and Structures. Montreal, Quebec, Canada, 11-14, Aug, 1996, 1027 pp.
• A. S. Ezeldin and P. N. Balaguru. 1992. Normal and High Strength Fiber-Reinforced Concrete Under Compression. Journal of Materials in Civil Engineering, Nov, Vol. 4, No. 4, pp. 415-429.
• A. S. Ezeldin and S. R. Lowe. 1991. Mechanical Properties of Steel Fiber Reinforced Rapid-Set Materials. ACI Materials Journal, Jul-Aug, Vol. 88, No. 4, pp. 384-389.
• D. A. Fanella and A. E. Naaman. 1985. Stress-Strain Properties of Fiber Reinforced Concrete in Compression. ACI Journal, Jul-Aug, Vol. 82, No. 4, pp. 475-483.
• H. Fattuhi. 1987. SFRC Corbel Tests. ACI Structural Journal, Mar-Apr, Vol. 84, No. 2, pp. 119-123.
• L. Franke. 1981. Behavior and Design of High-Quality Glass-Fiber Composite Rods as Reinforcement for Prestressed Concrete Members. Report, International Symposium, CP/Ricem/i Bk, Prague, 52 pp.
• C. Fritz, A. E. Naaman, and D.H.W. Reinhardt. 1992. Sifcon Matrix in RC Beams. Proceedings of the RILEM-ACI International Workshop, held June 23-26, 1991, Mainz, Germany; Ed. by H. W. Reinhardt and A. E. Naaman, E & FN Spoon, London, pp. 518-528.
• H. V. S. GangaRao, D. S. Altizer, P. V. Vijay, N. Douglass, and R. Pauer. 1995. Thermoset Polymer Performance under Harsh Environments to Evaluate Glass Composite Rebars for Infrastructure Application. Paper Presented at the 1996 ACI Spring Convention, Denver, Colorado, Mar 14-19, 1995.
• D. A. Gasparini, D. Verna, and A. Abdallah. 1989. Post Cracking Tensile Strength of Fiber Reinforced Concrete. ACI Materials Journal, Jan-Feb, pp 10-15.
• A. Gerritse and J. A. Den Uijl. 1995. Long-Term Behaviour of Arapree. Proceedings of the Second International RILEM Symposium, held on Aug. 23-25, 1995, Ghent, Belgium; Ed. by L. Taerwe; pp. 57-66.
• V. S. Gopalaratnam, S. P. Shah, and R. John. 1984. A Modified Instrumental Charpy Test for Cement Based Composites. Experimental Mechanics, Jun, Vol. 24, No. 2, pp. 102-110.
• S. Gopalaratnam and S. P. Shah. 1987. Tensile Failure of Steel Fiber Reinforced Mortar. Journal of Engineering Mechanics, May, Vol. 113, No. 5, pp. 635-652.
• L. E. Hackman, M. B. Farrell, and O. O. Dunham. 1992. Slurry Infiltrated Mat Concrete (SIMCON). Concrete International, Dec, pp 53-56.
• J. C. Halpin and S. W. Tsai. 1969. Effects of Environmental Factors on Composite Materials. AFML-TR 67423, Jun, 53 pp.
• D. J. Hannant. 1978. Fibre Cements and Fibre Concretes. John Wiley and Sons, Chichester, England, 219 pp.
• T. Hara and Y. Kitada. 1980. Shear Strength of Reinforced Concrete Corbels and Steel Fibers as Reinforcement. Transactions of the Japan Concrete Institute, Vol. 2, pp. 279-286.
• G. C. Hoff. 1985. Use of Steel Fiber Reinforced Concrete in Bridge Decks and Pavements. Steel Fiber Concrete, US-Sweden Joint Seminar (NSF-STU), Stockholm, Jun, pp. 67-108.
• G. C. Hoff. 1987. Durability of Fiber Reinforced Concrete in Severe Marine Environment. Proceedings, Katherine and Bryant Mather International Symposium on Concrete Durability. American Concrete Institute, Detroit, MI, Vol. 1, pp. 997-1041. (ACI SP-100)
• J. Houde, A. Prezeau, and R. Roux. 1987. Creep of Concrete Containing Fibers and Silica Fume. Fiber Reinforced Concrete Properties and Applications. American Concrete Institute, Detroit, MI, pp. 101-118. (ACI SP-105)
• L. S. Hsu and C-T. T. Hsu. 1994. Stress-Strain Behavior of Steel-Fiber High Strength Concrete Under Compression. ACI Materials Journal, July-Aug, Vol. 91, No. 4, pp. 448-457.
• S. Ibukiyama, S. Kokubun, and K. Ishikawa. 1989. Introduction of Recent Thin Bonded Concrete Overlay Construction and Evaluation of Those Performances in Japan. Proceedings of the 4th International Conference on Concrete Pavement Design and Rehabilitation, held on April 18-20, 1989, Purdue University, West Lafayette, IN, pp.193-203.
• S. L. Iyer and M. Anigol. 1991. Testing and Evaluating Fiber Glass, Graphite and Steel Cables for Pretensioned Beams. Advanced Composite Materials in Civil Engineering Structures. Proceedings of the Specialty Conference, ASCE, Las Vegas, Feb, pp. 44-56.
• C. D. Johnston. 1980. Properties of Steel Fiber Reinforced Mortar and Concrete. Proceedings of International Symposium on Fibrous Concrete (Cl-80). The Construction Press, Lancaster, England, pp. 29-47.
• C.D. Johnston. 1982. Definition and Measurements of Flexural Toughness Parameters for Fiber Reinforced Concrete. Cement, Concrete and Aggregates, Winter, Vol. 4, No. 2, pp. 53-60.
• C. D. Johnston and P. D. Carter. 1989. Fiber Reinforced Concrete and Shotcrete for Repair and Restoration of Highway Bridges in Alberta. Transportation Research Record, No. 1226, pp 7-16.
• C. D. Johnston and R. W. Zemp. 1991. Flexural Fatigue Performance of Steel Fiber Reinforced Concrete - Influence of Fiber Content, Aspect Ratio and Type. ACI Materials Journal, Jul-Aug, Vol. 88, No. 4, pp. 374-383.
• A. Khajuria, K. Bohra, and P. Balaguru. 1991. Long-Term Durability of Synthetic Fibers in Concrete. Durability of Concrete. Second International Conference, held in Montreal, Canada; Ed. by V.M. Malhotra; American Concrete Institute, Detroit, MI, Vol. 2, pp. 851-868. (ACI SP-126)
• H. Krenchel and B.H. Stang. 1988. Stable Microcracking in Cementitious Meterials. Second International Symposium on Brittle Composites, held September 1988, BMI, Cedzyna, Poland, pp. 20-33
• N. Krstulovic-Opara, C-M. Uang, and A. Hagayeghi. 1994. The Use of High Performance Cement Composites for Seismic Repair and Rehabilitation. Proceedings of the ASCE Materials Engineering Conference on Infrastructure: New Materials and Methods for Repair, held November 14-16, 1994, San Diego, CA, pp 812-819.
• D. R. Lankard and E. K. Shrader. 1983. Inspection and Analysis of Curl in Steel Fiber Reinforced Concrete Airfield Pavement. Bekaert Steel Wire Corp., Pittsburgh, 9 pp.
• D. R. Lankard and A. J. Walker. 1975. Pavement Applications for Steel Fibrous Concrete. Transportation Engineering Journal, Feb, Vol. 101, No. TE1, pp. 137-153.
• V. C. Li, S. Backer, Y. Wang, R. Ward, and E. Green. 1989. Toughened Behavior and Mechanisms of Synthetic Fiber Reinforced Normal Strength and High Strength Concrete. Fiber Reinforced Cements and Concretes: Recent Developments. International Conference, Sept. 18-20, University of Wales College, Cardiff, U.K.; Ed. by R.N. Swamy and B. Barr, Elsevier Applied Science, London, pp. 420-433.
• R. Y. Liang and E. Galvez. 1990. High Strength, High Denier Discrete Polymer Fiber in Cementitious Composites. Proceedings of the First Materials Engineering Congress, held Aug. 13-15, 1990, Denver, CO; Ed. by Bruce A. Suprenant, ASCE, New York, Vol. 2, pp. 894-902.
• T. Y. Lim, P. Paramavisam, and S. L. Lee. 1987. Analytical Model for Tensile Behavior of Steel Fiber Concrete. ACI Materials Journal, Jul-Aug, Vol. 84, No. 4, pp. 286-298.
• W. S. Lin and T. C. Hsu. 1990. Uni-axial and Bi-axial Compressive Fatigue of Fiber Concrete. Proceedings of the First Materials Engineering Congress, held on Aug 13-15, 1990, Denver,CO; Ed. by Suprenent; ASCE, New York, Vol. 2, pp.1172-1181.
• B. Malmberg and A. Skarendahl. 1978. Method of Studying the Cracking of Fibre Concrete Under Restrained Shrinkage. Testing and Test Methods of Fibre Cement Composites. RILEM Symposium, The Construction Press, Lancaster, England, 545 pp.
• P. S. Mangat and A. M. Azari. 1985. A Theory for the Creep of Steel Fibre Reinforced Cement Matrices Under Compression. Journal of Materials Science, pp. 1119-1133.
• M. A. Mansur, C. G. Ong, and P. Paramasivam. 1986. Shear Strength of Fibrous Concrete Beams without Stirrups. Journal of Structural Engineering, Vol. 112, No. 9, pp. 2066-2079.
• D. C. McKee. 1969. Properties of an Expansive Cement Mortar Reinforced with Random Wire Fibers. Ph.D. Thesis, University of Illinois, Urbana.
• S. Mindess and F. J, Young. 1981. Concrete. Prentice-Hall, Inc., Englewood Cliffs, N.J. pp. 521-522.
• K. Minosaku. 1991. Applications of FRP Materials to Prestressed Concrete Bridges and Other Civil Structures. Concrete Journal (Tokyo), Nov, Vol. 29, No. 11, pp. 56-63. (in Japanese)
• Mizutani, Noritake, Nakai, and Masuko. 1991. Design and Construction of Demonstration Bridge Using AFRP Rods as Tendons. Japan Concrete Institute Symposium on Effective Utilization of Prestress Theory and Technology, July, pp. (in Japanese)
• B. Mobasher, A. Castro-Montero, and S.P. Shah. 1990a. Study of Fracture in Fiber Reinforced Cement-Based Composites Using Laser Holographic Interferometry. Experimental Mechanics, Vol. 30, No. 6, pp. 286-294.
• B. Mobasher, C. Ouyang, and S.P. Shah. 1990b. High Performance Fiber Reinforced Cement-Based Composites. Serviceability and Durability of Construction Materials. Proceedings of First Materials Engineering Congress, held Aug. 13-15, 1990, Denver, CO; Ed. by Bruce A. Suprenant, ASCE, NY, Vol. 2, pp. 725-734.
• B. Mobasher, H. Stang, and S.P. Shah. 1990c. Microcracking in Fiber Reinforced Concrete. Cement and Concrete Research, Sep, Vol. 20, pp. 665-676.
• G. E. Monfore. 1968. A Review of Fiber Reinforcement of Portland Cement Paste, Mortar and Concrete. Journal of PCA Research and Development Laboratories, Sep, Vol. 10, No. 3, pp. 3642. (Also Research Development Bulletin No. 226, Portland Cement Association)
• D. R. Morgan. 1991. Freeze Thaw Durability of Steel and Polypropylene Reinforced Shotcretes: a Review. Durability of Concrete. Second International Conference, held in Montreal, Canada; Ed. by V.M. Malhotra; American Concrete Institute, Detroit, MI, Vol. 2, pp. 901-918. (ACI SP-126).
• A. A. Mufti, L. G. Jaeger, B. Bakht, and L. D. Wegner. 1993. Experimental Investigation of Fibre-Reinforced Concrete Deck Slabs Without Internal Steel Reinforcement. Canadian Journal Of Civil Engineering, Vol. 20, pp. 398-406.
• A. E. Naaman. 1985. High Strength Fiber Reinforced Cement Composites. Proceedings of MRS Symposium on Potential of Very High Strength Cement-Based Materials, Materials Research Society; Ed. by J. F. Young; Vol. 42, pp. 217-229.
• A. E. Naaman. 1987. High Performance Fiber Reinforced Cement Composites. Concrete Structures for the Future. IABSE Symposium, Paris, pp 371-376.
• A. E. Naaman, F. M. Al-khairi, and H. Hammoud. 1993. Mechanical Behavior of High Performance Concretes, Volume 6: High Early Strength Fiber Reinforced Concrete (HESFRC). Strategic Highway Research Program, National Research Council, Washington, D. C., xix, 297 pp. (SHRP-C-366)
• A. E. Naaman, F. Moavenzadeh, and F. McGarry. 1974. Probabilistic Analysis of Fiber Reinforced Concrete. Journal of Engineering Mechanics, Apr, Vol. 100, No. EM2, pp. 397-413.
• A. E. Naaman and S. P. Shah. 1976. Pull-Out Mechanisms in Steel Fiber-Reinforced Concrete. Journal of Structural Engineering, Aug, Vol. 102, No. ST8, pp. 1537-1548.
• M. Nagabhushanam, V. Ramakrishnam, and G. Vondran. 1989. Fatigue Strength of Friblillated Polypropylene Fiber Reinforced Concrete. Transportation Research Record, No. 1226, pp. 36-47
• Nagata and Sekijima. 1988. Application of New Base Material Reinforcing Mesh to Retaining Wall Shotcrete of Underground LPG Storage Tank. Concrete Journal, Sep, Vol. 26, No. 9, (in Japanese).
• H. Najm and A. E. Naaman. 1995 Prediction Model for Elastic Modulus of High Performance Fiber Reinforced Cement Composites. ACI Materials Journal, May-Jun, Vol.92, No. 3, pp. 304-314.
• H. Nakagawa, S. Akihama, and T. Suenaga. 1989. Mechanical Properties of Various Types of Fiber Reinforced Concretes. Fiber Reinforced Cements and Concretes: Recent Developments. International Conference held on Sept. 18-20, 1989, University of Wales College of Cardiff; Ed. by R.N. Swamy and B. Barr, Elsevier Applied Science, London, pp. 523-532.
• G. C. Nammur and A. E. Naaman. 1986. Strain Rate Effects on Tensile Properties of Fiber Reinforced Concrete. Proceedings of MRS Symposium on Cement Based Composites, Materials Research Society, Vol. 64, pp. 97-118.
• A. Nanni. 1988. Splitting-Tension Test For Fiber Reinforced Concrete. ACI Materials Journal, Jul-Aug, Vol. 81, No. 4, pp. 229-233.
• A. Nanni. 1989. Abrasion Resistance of Roller Compacted Concrete. ACI Materials Journal, Nov-Dec, Vol. 86, No. 6, pp. 559-565.
• A. Nanni and Z. Johari. 1989. RCC Pavement Reinforced With Steel Fibers. Concrete International, Mar, pp. 64-69.
• R. Narayanan and A. S. Kareen-Palanjian. 1986. Factors Influencing the Strength of Steel Fiber Reinforced Concrete. Proceedings of RILEM Symposium FRC 86, held in July 1986 at University of Sheffield, Sheffield, England.
• K. W. Neale and P. Labossiere (Ed.) 1992. Proceedings of the 1st International Conference — Advanced Composite Materials in Bridges and Structures. Sherbrook, Quebec, Canada, 705 pp.
• L. E. Nielsen and P. E. Chen. 1968 Young's Modulus of Composites Filled with Randomly Oriented Fiber. Journal of Materials, Jun, Vol. 3, No. 2, pp. 352-358.
• D. E. Otter and A. E. Naaman. 1988. Fiber Reinforced Concrete Under Cyclic and Dynamic Compression Load. Research Report, No. UMCE 88-9, Department of Civil Engineering, University of Michigan, Ann Arbor, 178 pp.
• A. M. Pailleve, M. Buil, and J. J. Serrano. 1989. Effect of Fiber Addition on the Autogenous Shrinkage of Silica Fume Concrete. ACI Materials Journal, Mar-Apr, Vol. 86, No. 2, pp. 139-144.
• F. Parker, Jr. and W. L. Shoemaker. 1991. PCC Pavement Patching Materials and Procedures. Journal of Materials in Civil Engineering, Feb, Vol. 3, No. 1, pp.29-47.
• M. E. Patton and W.L. Whittaker. 1983. Effect of Fiber Content and Damaging Load on Steel Fiber Reinforced Concrete Stiffness. ACI Journal, Jan-Feb, Vol. 80, No. 1, pp. 13-16.
• K. Paul, M. Polivka and M. K. Mehta. 1981. Properties of Fiber Reinforced Shrinkage-Compensating Concrete. ACI Journal, Nov-Dec, Vol. 78, No. 6, pp. 488-492.
• V. Ramakrishnan, P. Balaguru, L. Kostaneski, and D. Johnston. 1991. Field Performance of Fiber Reinforced Concrete Highway Pavements. Serviceability and Durability of Construction Materials. Proceedings of First Materials Engineering Congress, held Aug. 13-15, 1990, Denver, CO; Ed. by Bruce A. Suprenant, ASCE, NY, Vol. 2, pp. 903-912.
• V. Ramakrishnan, S. Gallapudi, and R. Zelles. 1987a. Performance Characteristics and Fatigue Strength of Polypropylene Fiber Reinforced Concrete. Fiber Reinforced Concrete Properties and Applications, American Concrete Institute, Detroit, MI, pp. 159-177. (ACI SP-105)
• V. Ramakrishnan, G. Oberling, and P. Tatnall. 1987b. Flexural Fatigue Strength of Steel Fiber Reinforced Concrete. Fiber Reinforced Concrete Properties and Applications, American Concrete Institute, Detroit, MI, pp. 225-245. (ACI SP-105)
• V. Ramakrishnan, G. Y. Wu, and G. Hosalli. 1989a. Flexural Behavior and Toughness of Fiber Reinforced Concretes. Transportation Research Record, No. 1226, 1989, pp. 69-77.
• V. Ramakrishnan, G. Y. Wu, and G. Hosalli. 1989b. Flexural Fatigue Strength, Endurance Limit, and Impact Strength of Fiber Reinforced Concretes. Transportation Research Record, No. 1226, pp. 17-24.
• H. W. Reinhardt and A. E. Naaman (Ed.). 1992. High Performance Fiber Reinforced Cement Composites. Proceedings of the International Workshop held by RILEM, ACI and others, June 23-26, 1991, Mainz, Germany; Ed. by H.W. Reinhardt and A.E. Naaman; E &FN Spon, London, xviii, 565 pp. (RILEM Proceedings Vol.15).
• S. H. Rizkalla and G. Tadros. 1994. A Smart Highway Bridge in Canada. Concrete International, Jun, pp. 42-44.
• J. P. Romualdi and G. B. Batson. 1963. Mechanics of Crack Arrest in Concrete. Journal of Engineering Mechanics, Jun, Vol. 89, No. EM3, pp. 147-168.
• J. P. Romualdi and J. A. Mandel. 1964. Tensile Strength of Concrete Affected by Uniformly Distributed Closely Spaced Short Lengths of Wire Reinforcement. ACI Journal, Jun, Vol. 61, No. 6, pp. 657-671.
• E. K. Schrader. 1984. Design Methods for Pavements With Special Concretes. Fiber Reinforced Concrete. American Concrete Institute, Detroit, MI, pp. 197-212. (ACI SP-81)
• E. K. Schrader. 1985. Fiber Reinforced Concrete Pavements and Slabs. Steel Fiber Concrete, US-Sweden Joint Seminar (NSF-STU), Stockholm, Jun, pp. 109-131.
• M. Schupack. 1985. Durability of Steel Fiber Reinforced Concrete Exposed to Severe Environments. Steel Fiber Concrete, US-Sweden Joint Seminar (NSF-STU), Stockholm, Jun, pp. 479-496.
• M. M. Schwartz. 1992. Composite Materials Handbook. McGraw-Hill, Inc, New York.
• K. Sekijima and H. Hiraga. 1990. Fiber Reinforced Plastics Grid Reinforcement for Concrete Structures. Proceedings of the IABSE Symposium, Brussels, pp. 593-598.
• R. Sen, D. Mariscal, and M. Shahawy. 1993. Investigation of S-2 Glass/Epoxy Strands in Concrete. Proceedings of ACI Symposium, held on Mar 28-31, 1993, Vancouver, Canada; Ed. by A. Nanni and C. W. Dolan; pp. 15-34. (ACI SP 138)
• S. P. Shah. 1991. Do Fibers Increase the Tensile Strength of Cement-Based Matrixes? ACI Materials Journal, Nov-Dec, Vol. 88, No. 6, pp. 595-602.
• S. P. Shah and M. Grzybowski. 1989. Shrinkage Cracking of Fiber Reinforced Concrete. NSF Center for Science and Technology of Advanced Cement-Based Materials. (Private Communication)
• S. P. Shah and A. E. Naaman. 1976. Mechanical Properties of Glass and Steel Fiber Reinforced Motar. ACI Journal, Jan, Vol. 73, No. 10, pp. 50-53.
• S. P. Shah and B.V. Rangan. 1970. Effect of Reinforcement on Ductility of Concrete. Journal of Structural Engineering, Jun, Vol. 96, No. ST6, pp. 1167-1184.
• S. P. Shah and B. V. Rangan. 1971. Fiber Reinforced Concrete Properties. ACI Journal, Feb, Vol. 68, No. 2, pp. 126-135.
• P. Shah, P. Stroeven, D. Dalhuisen, and P. Van Stekelenburg. 1978. Complete Stress-Strain Curves for Steel Fiber Reinforced concrete in Uniaxial Tension and Compression. Testing and Test Methods of Fibre Cement Composites. RILEM Symposium. The Construction Press, Lancaster, England, pp. 399-408.
• D. J. Stevens, N. Banthia, V. S. Gopalaratnam, and P. C. Tatnall (Ed.). 1995. Testing of Fiber Reinforced Concrete. American Concrete Institute, Detroit, MI, 254 pp. (ACI SP 155)
• J. Sustersic, E. Mali, and S. Urbancic. 1991. Erosion-Abrasion Resistance of Steel Fiber Reinforced Concrete. Durability of Concrete. Second International Conference, held in Montreal, Canada; Ed. by V.M. Malhotra; American Concrete Institute, Detroit, MI, Vol. 2, pp. 729-743. (ACI SP-126)
• R. N. Swamy. 1985. Steel Fibre Concrete for Bridge Decks and Building Floor Applications. Steel Fiber Concrete, US-Sweden Joint Seminar (NSF-STU), Stockholm, Jun, pp. 443-473.
• R. N. Swamy, R. Jones, and T. Chiam. 1987. Shear Transfer in Steel Fiber Reinforced Concrete. Fiber Reinforced Concrete Properties and Applications. American Concrete Institute, Detroit, MI, pp. 565-592. (ACI SP-105)
• R. N. Swamy and P. S. Mangat. 1974. Influence of Fibers Geometry on the Properties of Steel Fiber Reinforced Concrete. Cement and Concrete Research, Vol. 4, No. 3, pp. 451-465.
• R. N. Swamy, P. S. Mangat, and C. V. S. K. Rao. 1974a. The Mechanics of Fiber Reinforcement of Cement Matrices. Fiber-Reinforced Concrete. American Concrete Institute, Detroit, MI, pp. 1-28. (ACI SP-44)
• L. R. Taerwe. 1992. Influence of Steel Fibers on Straing Softening of High-Strength Concrete. ACI Materials Journal, Jan-Feb, Vol. 89, No. 1, pp. 54-60.
• L. Taerwe (Ed.). 1995. Proceedings of the 2nd International RILEM Symposium (FRPRCS - 2) — Non-Metallic (FRP) Reinforcement for Concrete Structures. Ghent, Belgium, 23-25 Aug, 1995, 714 pp.
• Tamura and Tezuka. 1990. Outline of Prestressed Concrete Bridge Using Aramid Fiber in Talbus Golf Course. Public Works, Vol. 31, No. 9, pp. 37-40. (in Japanese)
• K. H. Tan and M. A. Mansur. 1990. Shear Transfer in Reinforced Fiber Concrete. Journal of Materials in Civil Engineering, Nov, Vol. 2, No. 4, pp. 202-214.
• Tatsumi, Sekijima, Abe, and Subo. 1989. Application of Lattice-Form FRP Reinforcement to Concrete Fender. Proceedings of the 44th Annual Conference of the Japan Society of Civil Engineers, Vol. VI, pp. 238-239. (in Japanese)
• M. Valle. 1991. Shear Transfer in Fiber Reinforced Concrete. MS Thesis, Department of Civil and Environmental Engineering, Massachusetts Institute of Technology.
• M. Valle and O. Buyukozturk. 1993. Behavior of Fiber Reinforced High-Strength Concrete Under Direct Shear. ACI Materials Journal, Mar-Apr, Vol. 90, No. 2, pp. 122-133.
• M. P. Vandenberghe and D. E. Nemegeer. 1985. Industrial Flooring With Steel Fiber Reinforced Concrete. Concrete International, Mar. Vol. 7, No. 3, pp. 54-57.
• S. Vares. 1994. Frost Resistance of Steel Fiber High Strength Concrete. Nordic Concrete Reaserch, Publication No 15, pp. 75-88.
• K. Visalvanich and A. E. Naaman. 1983. Fracture Model for Fiber Reinforced Concrete. ACI Journal, Mar-Apr, Vol. 80, No. 2, pp. 128-138.
• Y. Wang, V. C. Li, and S. Backer. 1990. Experimental Determination of Tensile Behavior of Fiber Reinforced Concrete. ACI Materials Journal, Sept-Oct, Vol. 87, No. 5, pp. 461-468.
• R. J. Ward and V. C. Li. 1990. Dependence of Flexural Behavior of Fiber Reinforced Motar on Material Fracture Resistance and Beam Size. ACI Materials Journal, Nov-Dec, Vol. 87, No. 6, pp. 627-637.
• G. R. Williamson. 1974. The Effect of Steel Fibers on the Compressive Strength of Concrete. Fiber Reinforced Concrete, American Concrete Institute, Detroit, MI, pp. 195-207. (ACI SP-44)
• W. P. Wu, S. S. Faza, and H. V. S. Ganga Rao. 1991. Mechanical Properties of Fiber Reinforced Plastic (FRP) Bars for Concrete Reinforcement. Report, Constructed Facilities Center, West Virginia University, 40 pp.
• Yamamoto et al. 1989. Characteristics of Braided FRP Rock Bolts. Proceedings of the 44th Annual Conference of the Japan Society of Civil Engineers, Vol. VI, pp. 146-147. (in Japanese)
• W. S. Yin and C-T. T. Hsu. 1995. Fatigue Behavior of Steel Fiber Reinforced Concrete under Uniaxial and Biaxial Compression. ACI Materials Journal, Jan-Feb, Vol. 92, No. 1, pp. 71-81.
• Q. Zheng and D. D. L. Chung. 1989. Carbon Fiber Reinforced Cement Composites Improved by Using Chemical Agents. Cement and Concrete Research, Vol. 19, pp. 25-41.
• R. F. Zollo. 1972. Wire Fiber Reinforced Concrete Overlays for Orthotropic Bridge Deck Type Loading. ACI Journal, Oct, Vol. 72, No. 10, pp. 576-582.