Prediction of the Expected Safety Performance of Rural Two-Lane Highways
2. OVERVIEW OF THE ACCIDENT PREDICTION ALGORITHM
This section of the report presents an overview of the accident prediction algorithm for rural two-lane highways. Separate accident prediction algorithms have been developed for roadway segments and for three types of at-grade intersections. These separate algorithms can be used together to predict the total accident experience for an entire highway section or improvement project.
In the development of these algorithms, it was decided the roadway segment accident prediction algorithm would predict all non-intersection-related accidents for each of the segments that make up a highway project. Non-intersection-related accidents include accidents that occur near an intersection but are not related to the intersections. For example, a ran-off-road accident or a head-on collision that occurs within 15 m (50 ft) of an intersection, but it considered by the investigating officer to be unrelated to the intersection, would be classified as a non-intersection-related accident. The intersection accident prediction algorithms predict the additional intersection-related accidents that occur at or rear the intersection and occur because of the presence of the intersection. For modeling purposes, only accidents that occurred within 76 m (250 ft) of the intersection and occurred because of the presence of the intersection were considered to be intersection- related accidents. The total predicted accident frequency for any highway project is the sum of the predicted frequency of non-intersection-related accidents for each of the roadway segments and the predicted frequency of intersection-related accidents for each of the at-grade intersections that make up the project.
The accident prediction algorithms for roadway segments and at-grade intersections are each composed of two components: base models and accident modification factors. These components and the manner in which they are combined are described below.
Accident Prediction Algorithm for Roadway Segments
The base model for roadway segments is the best available regression model for predicting the total accident frequency of a roadway segment on a rural two-lane highway. The base model, like all regression models, predicts the value of a dependent variable as a function of a set of independent variables. For the roadway segment model, the dependent variable is the total expected accident frequency on the roadway segment during a specified time period. The independent variables used to predict accident frequency are descriptors of the traffic volumes, geometric design features, and traffic control features of the roadway segment. The specific regression model to be used as the base model for rural two-lane roadway segments is presented in section 3 of this report.
As discussed in the introduction to this report, regression models like the base model are useful in predicting overall accident frequency, but their coefficients cannot necessarily be relied upon to represent the incremental effects of individual geometric design and traffic control features. Therefore, the base model will be used only to estimate the expected accident frequency for a specified set of nominal base conditions, such as 3.6-m (12-ft) lane widths and 1.8-m (6-ft) shoulder widths. This base estimate of accident frequency will then be adjusted with accident modification factors (AMFs) that represent the safety effects of individual geometric design and traffic elements. The general formulation of the algorithm predicting roadway segment accident frequency and combining the base models and AMFs is shown below:
|
Nrs = Nbr (AMF1r AMF2r ··· AMFnr)
|
(2)
|
where:
| Nrs |
=
|
predicted number of total roadway segment accidents per year after application of accident modification factors; |
| Nbr |
=
|
predicted number of total roadway segment accidents per year for nominal or base conditions; and |
|
AMF1r ··· AMFnr
|
=
|
accident modification factors for roadway segments. |
The AMFs are multiplicative factors used to adjust the base accident frequency for the effect of individual geometric design and traffic control features. Each AMF is formulated so that the nominal or base condition is represented by an AMF of 1.00. Conditions associated with higher accident experience than the nominal or base condition will have AMFs greater than 1.00 and conditions associated with lower accident experience than the nominal or base condition will have AMFs less than 1.00. For example, if the accident frequency predicted by the base model for roadway segments (Nbr) is based on 3.6-m (12-ft) lanes, but a particular roadway section of interest has 3.3-m (11-ft) lanes, the AMF for lane width might have a value of 1.15. This AMF implies that a two-lane roadway segment with 3.3-m (11-ft) lanes would be expected to experience 15 percent more accidents than a comparable roadway section with 3.6-m (12-ft) lanes.
The effect of average daily traffic (ADT) volume on predicted accident frequency is incorporated through the base models, while the effects of geometric design and traffic control features are incorporated through the AMFs.
The formulation shown in equation (2) allows the AMF for each geometric design and traffic control element to be based solely on the most reliable information concerning the safety effects of that particular element. The best method for considering the safety effects of lane width can be selected as the basis for the AMF without being constrained by the treatment of lane width in the base model or by the formulation of any other AMF. Thus, each AMF in the accident prediction algorithm can be based on the best and most applicable research available, as selected and interpreted by knowledgeable experts. In fact, two panels of experts, identified in appendix A, were formed to establish the AMFs presented in this report. Section 4 of the report presents the AMFs used in predicting roadway segment accidents and documents their development.
Accident Prediction Algorithm for At-Grade Intersections
The structure of the accident prediction algorithm for at-grade intersections is similar to the algorithm for roadway sections presented above. The predicted frequency of accidents that occur at or are related to an at-grade intersection is determined as:
|
Nint = Nbi (AMF1i AMF2i··· AMFni)
|
(3)
|
where:
| Nint |
=
|
predicted number of total intersection-related accidents per year after application of accident modification factors; |
| Nbi |
= |
predicted number of total intersection-related accidents per year for nominal or base conditions; and |
|
AMF1i' ··· ' AMFni
|
=
|
accident modification factors for intersections. |
Separate base models have been formulated for three-leg intersections with STOP control, four-leg intersections with STOP control, and four-leg signalized intersections. The AMFs used in the accident prediction algorithm for these three intersection types also differ, but the algorithms for all three intersection types are structured as shown in equation (3). The base models for at-grade intersections are presented in section 3 of this report, and the AMFs for at-grade intersections are presented in section 4.
The effect of traffic volume on predicted accident frequency for at-grade intersections is incorporated through the base models, while the effect of geometric and traffic control features are incorporated through the AMFs. Each of the base models for at-grade intersections incorporates separate effects for the ADTs on the major- and minor-road legs, respectively.
Predicted Accident Frequency for an Entire Project
The accident prediction algorithm will be applied in IHSDM to estimate the safety performance of entire proposed projects or extended highway sections. The total predicted accident frequency for an entire project or an extended highway section can be determined as:
|
Nt =
|
å
|
Nrs +
|
å
|
Nint
|
|
|
all
segments
|
|
all
intersections
|
|
where:
| Nt |
= |
predicted accident frequency for an entire project or an extended highway section. |
Estimated Accident Severity and Accident Type Distributions
In addition to predictions of accident frequency based on equations (2) and (3), the accident prediction algorithm will also provide estimates of the accident severity and accident type distributions for roadway segments and at-grade intersections. Tables 1 and 2 present default estimates of the accident severity and accident type distributions, respectively, that are used in the accident prediction algorithm. The default accident severity and accident type distributions in tables 1 and 2 are based on data from the FHWA Highway Safety Information System (HSIS) for Illinois, Michigan, Minnesota, and North Carolina. These default distributions for accident severity and accident type can be replaced with data suitable for the rural two-lane highway system of a particular highway agency as part of the calibration process described in section 3 and appendix D of this report. Use of distributions applicable to a specific State or geographic region is particularly appropriate because some percentages in the tables, such as the percentage of animal-related accidents on roadway segments in table 2, clearly vary geographically.
Strengths and Weaknesses of this Approach
The strengths of the accident prediction algorithms formulated as shown in equations (2) and (3) are as follows:
- The accident prediction algorithms make quantitative estimates of accident frequency.
- The base models serve as scale factors to assure that the magnitude of the predicted accident frequency is appropriate, while the AMFs assure that the predicted accident frequency is sensitive to site-specific geometric design and traffic control features.
- The use of AMFs that are separate from the base models assures that the effects of individual geometric design and traffic control features are not dependent on inappropriate regression coefficients that are too large, too small, or in the wrong direction. Each AMF has been developed by a panel of experts to represent the best information currently available on the safety effects of that particular geometric design or traffic control feature.
- Equations (2) and (3) give the accident prediction algorithm a modular structure. Individual base models or AMFs can be easily replaced as better information becomes available.
Table 1. Default Distribution for Accident Severity Level on Rural Two-Lane Highways
| |
Percentage of total accidents
|
| Accident severity level |
Roadway
segmentsa |
Three-leg STOP-
controlled
intersectionsb |
Four-leg
STOP-controlled
intersectionsb |
Four-leg
signalized
intersectionsb |
| Fatal |
1.3 |
1.1 |
1.9 |
0.4 |
| Incapacitating Injury |
5.4 |
5.0 |
6.3 |
4.1 |
| Nonincapacitating injury |
10.9 |
15.2 |
12.8 |
12.0 |
| Possible injury |
14.5 |
18.5 |
20.7 |
21.2 |
| Total fatal plus injury |
32.1 |
39.8 |
41.7 |
37.7 |
| Property damage only |
67.9 |
60.2 |
58.3 |
62.3 |
| TOTAL |
100.0 |
100.0 |
100.0 |
100.0 |
a Based on HSIS data for Illinois (1992), Michigan (1995), Minnesota (1996), and North Carolina (1995).
b Based on HSIS data for Michigan (1995) and Minnesota (1996).
Table 2. Default Distribution for Accident Type and Manner of Collision on Rural Two-Lane Highways.
|
Percentage of total accidents
|
| Accident type and manner of collision |
Roadway
segmentsa |
Three-leg STOP-controlled
intersectionsb |
Four-leg STOP-controlled
intersectionsb |
Four-legsignalized
intersectionsb |
| SINGLE-VEHICLE ACCIDENTS |
| Collision with animal |
30.9 |
2.1 |
0.6 |
0.3 |
| Collision with bicycle |
0.3 |
0.7 |
0.3 |
1.0 |
| Collision with parked vehicle |
0.7 |
0.1 |
0.1 |
0.1 |
| Collision with pedestrian |
0.5 |
0.4 |
0.2 |
1.3 |
| Overturned |
2.3 |
2.1 |
0.6 |
0.4 |
| Ran off road |
28.1 |
10.4 |
4.5 |
1.9 |
| Other single-vehicle accident |
3.6 |
3.9 |
1.4 |
1.6 |
| Total single-vehicle accidents |
66.3 |
19.7 |
7.7 |
6.6 |
| MULTIPLE-VEHICLE ACCIDENTS |
| Angle collision |
3.9 |
29.8 |
51.4 |
28.5 |
| Head-on collision |
1.9 |
2.0 |
1.4 |
1.8 |
| Left-turn collision |
4.2 |
6.4 |
5.9 |
9.0 |
| Right-turn collision |
0.6 |
0.4 |
0.2 |
0.4 |
| Rear-end collision |
13.9 |
26.2 |
17.2 |
36.2 |
| Sideswipe opposite-direction collision |
2.4 |
2.9 |
1.7 |
2.0 |
| Sideswipe same-direction collision |
2.6 |
4.5 |
4.4 |
5.5 |
| Other multiple-vehicle collision |
4.1 |
8.1 |
10.1 |
10.0 |
| Total multiple-vehicle accidents |
33.7 |
80.3 |
92.3 |
93.4 |
| TOTAL ACCIDENTS |
100.0 |
100.0 |
100.0 |
100.0 |
a Based on HSIS data for Illinois (1992), Michigan (1995), Minnesota (1996), and North Carolina (1995).
b Based on HSIS data for Michigan (1995) and Minnesota (1996).
The potential weaknesses of the structure for the accident prediction algorithms based on equations (2) and (3) are as follows:
- Accident frequencies are known to vary from agency to agency, even between roads that are nominally similar, because of differences in factors such as accident reporting thresholds, accident reporting practices, animal populations, driver population, and climate. However, such variations are not reflected in the base models that were each developed with data for only one or two States. For this reason, a calibration procedure has been provided in this report to allow highway agencies to adapt the accident prediction algorithm to their own local safety conditions. This calibration procedure involves the estimation of calibration factors appropriate for a particular highway agency that can be incorporated directly in equations (2) and (3).
- The accident prediction algorithm, as formulated in equations (2) and (3), is based on data for many locations and on expert judgment, but does not take advantage of knowledge of the actual accident history of the location being evaluated. Actual accident history data should be available for many existing locations evaluated with the accident prediction algorithm. For this reason, a procedure based on the Empirical Bayes (EB) approach is provided in this report to combine the results of the accident prediction algorithm with actual site-specific accident history data.
- The use of separate AMFs for each geometric design and traffic control element treats the safety effects of these individual elements as independent and ignores potential interactions between them. It is likely that such interactions exist and, ideally, they should be accounted for in the accident prediction algorithm. However, such interactions are poorly understood and none could be quantified by the expert panels that participated in this research. It is the assessment of the expert panels that the AMFs presented in this report represent the current state of knowledge about the safety effects of geometric design and traffic control elements and cannot be improved without further research. If future research leads to a better understanding of interactions between the safety effects of various geometric features, those research results can then be incorporated in the accident prediction algorithm.
Structure of the Accident Prediction Algorithm
The structure of the accident prediction algorithm, including base models, accident modification factors, calibration factors, and EB procedure is illustrated in figure 1. The flow diagram in figure 1 addresses the application of the accident prediction algorithm to a single roadway segment or at-grade intersection. Section 6 of the report illustrates the application of the algorithm to a project made up of numerous roadway segments and intersections.
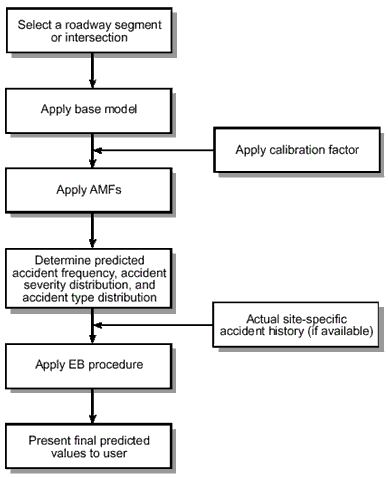
Figure 1. Flow Diagram of the Accident Prediction Algorithm for a Single Roadway Segment or Intersection
Previous | Table of Contents | Next
|
