Technical Advisories
Specification Conformity Analysis
T 5080.12
June 23, 1989
Par.
- Purpose
- References
- Background
- Application
- Discussion
- Concepts
Attachment 1, List of References
Attachment 2, Calculation Procedures and Example
- PURPOSE. To provide guidance on the technical basis for, and the use of Specification Conformity Analysis (SCA) procedures (formerly called Quality Level Analysis (QLA)).
- REFERENCES. A listing of references and additional publications pertaining to statistics and SCA procedures is provided as Attachment 1 to this Technical Advisory.
- BACKGROUND
- The QLA (now called SCA) procedure was developed by the FHWA as a part of the Highway Condition and Quality of Highway Construction Surveys (1976-1982). It was used to estimate the degree of compliance with specifications and to provide an indication of construction quality on a nationwide basis. The terminology is being changed to SCA to better reflect the actual usage of the analysis procedure.
- The SCA procedure is being used in construction monitoring programs on a State-by-State basis where individual specification limits are held constant. The SCA procedure is also used by some States as an indicator of contractor performance in meeting specifications and/or as a basis for pay factor incentive and disincentive systems. In these cases, the specifications, sampling and testing programs, and contract documents have been written based on this type of acceptance. The concepts of the SCA procedure are consistent with those used in the AASHTO Guide Specification R9-86, "Standard Recommended Practice for Acceptance Sampling Plans for Highway Construction. "
- APPLICATION. The use of SCA procedures can be an integral part of a construction monitoring program for measuring conformity with specifications and for developing background information for improving specifications or construction procedures.
- The SCA procedure can be effectively used to estimate the degree of conformity to specification requirements that is being achieved on a project or for a particular construction process. It can be used as a tool during project or in depth inspections, or as a special effort, to analyze construction measurements or materials test results and evaluate the degree of specification compliance. It can be used in Statewide inspections or reviews, when specification limits are uniform, to evaluate specification compliance over several projects to ascertain whether there are widespread uniformity or process control problems.
- The SCA procedure can identify specification requirements which are impractical or ineffectual in assuring good performance. In cases of consistently low percent conformity over several projects, the specification limits should be analyzed with respect to how much material variance, sampling variance, and testing variance is inherent in the construction process under question. If the specification limits do not allow reasonable room for these variances, they are likely impractical for current procedures, and conformity levels will always be low.
- (1) A classic example of this situation can occur in the measurement of slump to determine the consistency of plastic concrete. Research has shown that for a reasonably well-controlled process, the overall standard deviation can be expected to be on the order of 1/2 inch. With specification tolerance limits of ±1/2 inch imposed, one could expect, over a period of time, to have approximately 32 percent of the test results out of specifications if the process is producing concrete with normal variability and the average slump is equal to the specified target value. Refer to Figure 3 on page 10.
- (2) In order to allow for normal variability due to sampling, testing, and inherent materials variations, the tolerance limits in this example should be set at ±1 inch (equal to two standard deviations) when judging conformity on the basis of one test. With these tolerance limits, approximately 95 percent conformity can be expected over a period of time. This will avoid having changes made when the processis really under control. Only when the precision of sampling and testing methods and normal production processes are improved would it be practical to tighten these tolerances.
- The SCA procedures are useful for relating the degree of conformity to specifications with product performance. If an element is not performing as expected, then an analysis of specification conformity is appropriate. In cases where the calculated percent conformity consistently and easily equals 100, the appropriateness of the specification should be explored. The target value should be reviewed, and the production variances compared to the historical or expected variance established by research. Improved performance may be achievable by improving the specification target if the relationship of the variable being measured to performance is known or by reducing the allowable deviation from the target specification to encourage more uniform production. A change in specification limits may also be accompanied by an increase in sample size to reduce the risk of making an erroneous decision, i. e. , reduce the risk of accepting nonspecification material. It may also be necessary to test for another characteristic which better predicts the performance desired.
- The SCA procedures are useful for evaluating contractors' process control capabilities. Calculated percent conformity can serve as a general indicator of a contractor's equipment capabilities, workmanship, management, and overall desire to produce a specification product. The procedure consists of computing the percent conformance for selected construction phases or materials production and their respective properties, and maintaining a log of the percent conformance by contractor over a period of time or over a number of projects. By so doing, those contractors who adhere most closely to specification requirements can be identified.
- The SCA procedures are useful for monitoring the degree ofcontrol over a period of time. Project test data from several projects can be collected and stored over a long period of time. It is possible to investigate production variability for various materials and conditions by analyzing collected data independently of the specification limits for statistical measures such as averages and standard deviation, and by building a history of this data from actual construction projects. Similarly, cases can be identified where improvements in quality control are needed by comparing actual variations (standard deviations) to expected historical variations. The information gathered can be used to create or modify specifications. Care is needed regarding random sampling as discussed in paragraph 5c.
- The SCA procedures can be used to determine when to increase or decrease sampling and testing frequencies from the approved frequencies. If the calculated percent conformity is consistently high and it has been determined that the specifications are adequate to produce the performance desired, sampling frequencies could be reduced on a project basis. Conversely, if the calculated percent conformance is low and the same specification conditions exist as above, frequencies might be increased to reduce the risk of accepting nonspecification material.
- The SCA procedures are being used successfully by some States and on Direct Federal projects in specifications for the acceptance of materials, most notably asphalt concrete. The use of SCA procedures for this purpose must be implemented carefully. Material and production variations for the specific materials or work items, characteristics to be measured to predict performance, specification limits, process control and acceptance sampling and testing responsibilities, and pay factors are all items which must be carefully determined when developing specifications and acceptance procedures.
- DISCUSSION
- In making use of the SCA procedure, it is helpful to havesome knowledge of the overall variability inherent in the highway construction processes, the variability inherent in the natural makeup of materials, the variability associated with sampling and testing, and the effect these variabilities have on performance. This information may be available in a particular State from research on specific materials or from research done on a broader basis. A good source of information on materials variations is the reports resulting from early research by the Office of Research and Development of the Bureau of Public Roads (now Federal Highway Administration) entitled, "Quality Assurance in Highway Construction" which were published in Public Roads, Vol. 35, Nos. 6-11, February 1969.
- The SCA procedure gives a statistical estimate of the degree of conformity to specification requirements, not an absolute measure. All work would have to be tested or measured to be 100 percent sure that all material or work meets specification requirements. The results of SCA calculations are sensitive to sample size. The larger the sample size, the higher the degree of confidence one can have that the calculated percent conformity reflects the true degree of conformity of the construction process to the specifications.
It is important to keep in mind that these procedures assume that tests and/or measurements are taken on a statistically random basis. This means that each element of work has an equal chance of being selected for testing. An SCA performed on test results of samples taken on a judgment basis should not be construed to reflect the calculated percent conformity of the total project or process because the samples are probably biased, either toward good or poor construction. The results of an SCA made on test results of samples selected on a judgment basis reflect the calculated percent conformity being produced at a particular place or point in time and are biased by the judgment of the person doing the sampling. This does not mean, however, that the SCA procedures should not be used when random sampling has not been used. It does mean that caution is necessary when using data taken under these conditions, especially data collected for determining variances of production or construction processes.
All test results should be available for use. If retesting is done without performing any corrective work on the product and the original test results are not included, the calculated percent conformity will be erroneous and misleading. It is important that the test results actually represent the population being analyzed.
- The SCA procedure is a statistical tool and its use in evaluating construction activities is based on certain assumptions. Since the SCA procedure only estimates the degree of conformity with a particular specification, it is not a direct measure of quality when viewed in terms of eventual performance. A high calculated percent conformity is more indicative of good performance when all the following factors are present: when the quality of design is high, when the specification and other contract requirements adequately reflect properties and/or limits that ensure a good quality of performance and workmanship, and when the measured attributes relate to performance. Table 1 illustrates the importance of each component of the process in achieving good performance.
- In summary, the SCA procedure, when properly used, gives an estimate of the degree of conformity to specification requirements for the construction process and/or material to which it is applied. The test results and/or measurements used in the SCA should be randomly selected and accurate for the results to be totally valid. In order to infer whether or not good performance will likely result, the measured attributes and the specification requirements must be related to the properties which control performance. Care must also be exercised when comparing SCA results among processes, projects, or States. Comparisons are invalid unless the same specification requirements have been used in the individual analyses.
TABLE 1
| QUALITY LEVEL | QUALITY OF DESIGN | ACTUAL LOAD APPLICATIONS | SERVICE CONDITIONS | END PRODUCT PERFORMANCE | PROBABLE CAUSE |
|---|---|---|---|---|---|
| Low | Proven | As Designed | As Designed | Poor | Nonspecification Compliance |
| High | Proven | As Designed | As Designed | Poor | Specification criteria meaningless as related to performance |
| High | Questionable | As Designed | As Designed | Poor | Design process is not valid |
| High | Proven | Unknown | As Designed | Poor | Likely related to overstressing |
| Low | Proven | As Designed | As Designed | Good | Specification criteria likely over restrictive or meaningless as related to performance |
| High | Proven | As Designed | As Designed | Good | Well-designed system |
- CONCEPTS
- Research has shown that statistical methods can be applied to test values and measurements of most highway construction materials and work items. This research has also shown that the variation in the production of these materials conforms closely to a standard curve that is commonly used in statistical analyses. This standard curve is known as a "bell shaped" or "normal" curve, and represents the frequency of encountering a particular value. The normal curve is a symmetrical, bell-shaped curve that is centered on the average of all values representing a single process or production, and has a base width that is a direct function of how widely the individual values vary. This base width is referred to as the total variability of the population.
- Earlier versions of the SCA calculation procedure were based on the range of the test values (the difference between the minimum and maximum value) as the measure of variability. The current version uses the standard deviation as the measure of variability. The range method was chosen initially because of the simple calculations and ease of use of the method since the calculations were performed manually. With the advent of computers and inexpensive calculators that have the standard deviation function, the disadvantage of lengthy calculations associated with the standard deviation method have now been removed. The standard deviation method is more statistically efficient, requiring smaller sample sizes to provide an equivalent degree of assurance. It is less sensitive than the range to possible outliers because it is computed from all the data values, rather than the two extreme values. The standard deviation method avoids the need for the subgrouping rules advocated with the range method and has better mathematical properties for varioussubsequent statistical analyses that might be performed.
- The construction or material resulting from a single process or production is generally known as the "population. " As the variability, or standard deviation, of the population increases or decreases, the base width of the normal curve increases or decreases correspondingly.
Figures 1 and 2 (below) illustrate this point. Distribution curves for three different populations of densities are shown in Figure l that have the same average values (x) but different variabilities. The population variability is represented by the Greek letter sigma (
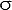 ), meaning "standard deviation. "
), meaning "standard deviation. "Figure 1
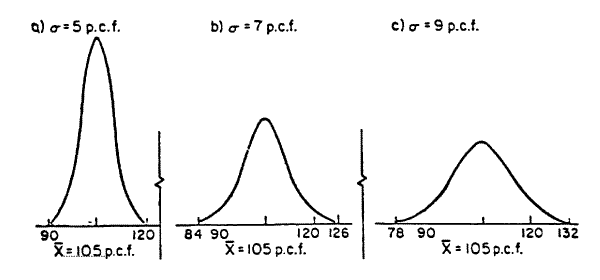
Figure 2
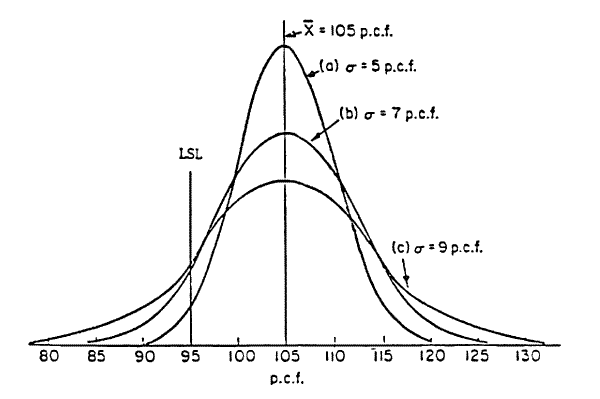
The distribution curves for the three populations shown in Figure 1, are superimposed in Figure 2 to graphically represent the effect of increased variability. If the lower specification limit (LSL) for the example material illustrated in Figure 2 is established at 95 pounds per cubic foot (pcf), the area under the distribution curves to the right of the LSL represents that part of the production that is greater than the LSL. As illustrated in Figure 3 (below), the area under any distribution curve is defined to be unity (generally accepted to be between X ± 3
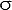 ), or 1.0. Since the area under the entire curve represents 100 percent of the population, that portion of the area under the curve that is to the right of the LSL represents the percent of the population that is in compliance with the specifications. Conversely, the area under the curve to the left of the LSL represents the percent of the population which is not in compliance with the specifications. By using established statistical procedures and with the average value (X) and variability (
), or 1.0. Since the area under the entire curve represents 100 percent of the population, that portion of the area under the curve that is to the right of the LSL represents the percent of the population that is in compliance with the specifications. Conversely, the area under the curve to the left of the LSL represents the percent of the population which is not in compliance with the specifications. By using established statistical procedures and with the average value (X) and variability (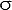 ) of each population known, the percent of each population that is greater than the LSL can be determined. For example, the percent of the population that is greater than the LSL for distribution curve (a) is 98 percent,since the LSL is -2
) of each population known, the percent of each population that is greater than the LSL can be determined. For example, the percent of the population that is greater than the LSL for distribution curve (a) is 98 percent,since the LSL is -2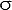 from the population average. For curve (b), the percent of the population that is greater than the LSL is 92 percent, and similarly for curve (c), the percent of the population greater than the LSL is 87 percent. Therefore, the calculated percent conformity for each of the example populations would be 98, 92, and 87 respectively. Attachment 2 shows the mechanics for making these kinds of computations.
from the population average. For curve (b), the percent of the population that is greater than the LSL is 92 percent, and similarly for curve (c), the percent of the population greater than the LSL is 87 percent. Therefore, the calculated percent conformity for each of the example populations would be 98, 92, and 87 respectively. Attachment 2 shows the mechanics for making these kinds of computations.Figure 3
Percentage of Area Within Given Standard Deviation Limits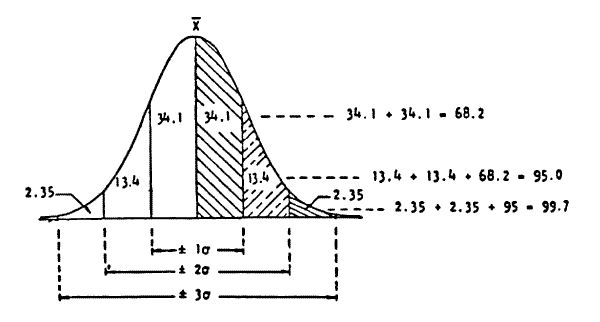
- Therefore, by using established statistical procedures, the percent of the population that is within specifications limits (the calculated percent conformity) can be determined if the average and the variability of the population are known. However, the average and variability (standard deviation) of the population are generally not known and, therefore, must be determined either from research, historical data, or estimated from calculations based on a sufficient number of samples or measurements of the population.
- Estimating the average and variability of the population from construction data often means that the estimates must be based on small numbers of samples. The SCA calculation procedure as embodied in the software (QLA, version II) previously distributed to all field offices, uses a methodology which needs only a small number of samples from the population to make these estimates. Test data is usually readily available from project records and relatively simple calculations are then required. The procedure used to calculate the standard deviation of the samples (s) is based on the "beta" distribution which is most applicable to small sample sizes (n < 30). The "beta" distribution is also applicable for larger sample sizes. Indices are computed using the average and standard deviation of the sample test values and the upper and lower specification limits. These indices represent the number of standard deviations the upper and lower specification limits are from the average of the test values, commonly referred to as "Z" values. Using the number of samples (n) and the calculated indices, aspecial statistical table (Table 1 of Attachment 2) is consulted to obtain the percent of the population, from which the test samples were drawn, which is estimated to be within specification limits. This calculation yields the area under a normal curve, between upper and lower specification limits, described by the average
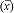 and the standard deviation of the samples (s) from the population.
and the standard deviation of the samples (s) from the population.
E. Dean Carlson
Associate Administrator for
Engineering and Program
Development
References
1. "Construction Inspection Techniques," Construction and Maintenance Division, Federal Highway Administration, 1986.
2. Doty, Leonard A. , "Reliability for the Technologies," Industrial Press, Inc. , New York, 1985.
3. "Handbook of Applications of Statistical Concepts to the Highway Construction Industry," Parts 1-2, Materials Research and Development, Inc. , MAT-DES-DEV-WGAI-7l-660-1, 1971.
4. "Highway Condition and Quality of Highway Construction Survey," Instruction Manual, Federal Highway Administration, 1985.
5. "Sampling Procedures and Tables for Inspection by Variables for Percent Defective," Military Standard 414, Department of Defense, June 1957.
6. Willenbrock, Jack H. , "A Manual for Statistical Control of Highway Construction, Volumes I and II," Federal Highway Administration, NHI, January 1976.
7. "Standard Recommended Practice for Acceptance Sampling Plans for Highway Construction, AASHTO Designation R9-86," American Association of State Highway and Transportation Officials (AASHTO), 1986.
8. McMahon, Thurmul F. , and Halstead, Woodrow J. , "Quality Assurance in Highway Construction," Public Roads, Vol. 35, Nos. 6-11, February 1969.
Attachment 2
Specification Conformity Analysis Calculation Procedure and Example
This attachment explains the procedure used to compute the percent conformity of a given set of test results using the standard deviation approach. It is shown here to both explain the manual calculation steps and to help the user understand how the computer program for computing percent conformity (QLA, version II) works. After the test data is input, the computer program will compute the percent conformity for each item and provide a convenient method of storing, editing, accumulating, and analyzing the data. More detailed information on the features of the program are included in the operations manual which accompanies it.
The calculation procedure illustrated in steps 2 and 3 can be facilitated through the use of a calculator with statistical capabilities. Specifically the calculator must be able to compute the sample standard deviation which is commonly abbreviated "s" or "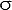 n-1. " If such a calculator is not available, the standard deviation can be computed using the tabular approach presented in this section.
n-1. " If such a calculator is not available, the standard deviation can be computed using the tabular approach presented in this section.
1. Randomly select a set of test data representing a minimum of 3 production days, if possible, with a minimum of two tests per production day. If only 1 day of production is used, a minimum of three tests is necessary. The upper and lower specification limits for the tests need to be known.
Example
The following set of data was collected from project test records for 3 production days of asphalt concrete paving:
| Production Day | Bitumen Content |
|---|---|
| 1 | 6.4, 6.6 |
| 2 | 6.0, 6.7 |
| 3 | 5.8, 6.2 |
The job-mix formula (JMF) target for individual test results is 6.2 percent, and specification limits are JMF + 0.4 and JMF - 0.4 percent.
2. Determine the average 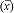 of the test results:
of the test results:
x = 6.4 + 6.6 + 6.0 + 6.7 + 5.8 + 6.2 = 6.28
6
3. Compute the sample standard deviation (s): [SEE PRINTED COPY FOR SAMPLE STANDARD DEVIATION]
An illustration of computing the standard deviation using the tabular approach
is presented below. Alternatively, calculators with statistical capabilities
can be used to compute the s value (this is also known as 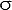 n-1).
n-1).
| Individual Test Results (x) | Mean 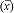 |
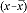 |
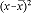 |
| 6.4 | 6.28 | 0.12 | 0.0144 |
| 6.6 | 6.28 | 0.32 | 0.1024 |
| 6.0 | 6.28 | -0.28 | 0.0784 |
| 6.7 | 6.28 | 0.42 | 0.1764 |
| 5.8 | 6.28 | -0.48 | 0.2304 |
| 6.2 | 6.28 | -0.08 | 0.0064 |
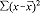 = = |
0.6084 |
[SEE PRINTED COPY OF TA FOR COMPLETE RESULTS]
4. Find the upper quality index (Qu) by subtracting the average (x) from the upper specification limit (U.L.) and dividing by the sample standard deviation (s).
[SEE PRINTED COPY OF TA FOR SAMPLE]
Example
The upper specification limit is 6.6 (6.2 + 0.4).
[SEE PRINTED COPY OF TA FOR EXAMPLE]
5. Find the lower quality index (QL) by subtracting the lower specification limit (L.L.) from the average and dividing by the sample standard deviation (s).
[SEE PRINTED COPY OF TA FOR SAMPLE]
Example
The lower specification limit is 5.8 (6.2 - 0.4).
[SEE PRINTED COPY OF TA FOR EXAMPLE]
6. Estimate the percent of material (Pu) that is below the upper specification limit by entering Table 1A or 1B with Qu and using the column appropriate to the total number of test results being analyzed.
Example
From Table 1A, the value of Pu corresponding to Qu = 0.91, and n = 6 can be found to be 81 percent.
7. Estimate the percent of material (PL) that will exceed the lower specification limit by entering Table 1A or 1B with QL and using the column appropriate to the total number of test results being analyzed.
Example
From Table 1A, the value of PL corresponding to QL = 1.37, and n = 6 can be found to be 93 percent.
8. Where both U.L. and L.L. specification limits are applicable, find the percent of material within these limits by adding the percent below the upper limit (Pu) to the percent above the lower limit (PL) and subtracting 100.
Example
Pt = (percent within limits) = (Pu + PL) - 100
Pt = (81 + 93) - 100 = 74 percent
This value represents the statistically predicted percent of the population to be within the specification limits.
9. Where only one specification limit is applicable, U.L. or L.L., the percent within limits is that value obtained directly from Table 1A or 1B, by using either Qu or QL as applicable.
Table 1A Specification Conformity Standard Deviation Method
| Upper Quality Index QU or Lower Quality Index QL | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PU or PL Percent within limits for positive values of QU or QL | n=3 | n=4 | n=5 | n=6 | n=7 | n=8 | n=9 | n=10 to n=11 | n=12 to n=14 | n=15 to n=18 | n=19 to n=25 | n=26 to n=37 | n=70 to n=69 | n=70 to n=200 | n=201 to n=inf | PU or PL Percent within limits for negative values of QU or QL |
| 100 | 1.16 | 1.50 | 1.79 | 2.03 | 2.23 | 2.39 | 2.53 | 2.65 | 2.83 | 3.03 | 3.20 | 3.38 | 3.54 | 3.70 | 3.83 | 0 |
| 99 | - | 1.47 | 1.67 | 1.80 | 1.89 | 1.95 | 2.00 | 2.04 | 2.09 | 2.14 | 2.18 | 2.22 | 2.26 | 2.29 | 2.31 | 1 |
| 98 | 1.15 | 1.44 | 1.60 | 1.70 | 1.76 | 1.81 | 1.84 | 1.86 | 1.91 | 1.93 | 1.96 | 1.99 | 2.01 | 2.03 | 2.05 | 2 |
| 97 | - | 1.41 | 1.54 | 1.62 | 1.67 | 1.70 | 1.72 | 1.74 | 1.77 | 1.79 | 1.81 | 1.83 | 1.85 | 1.86 | 1.87 | 3 |
| 96 | 1.14 | 1.38 | 1.49 | 1.55 | 1.59 | 1.61 | 1.63 | 1.65 | 1.67 | 1.68 | 1.70 | 1.71 | 1.73 | 1.74 | 1.75 | 4 |
| 95 | - | 1.35 | 1.44 | 1.49 | 1.52 | 1.54 | 1.55 | 1.56 | 1.58 | 1.59 | 1.61 | 1.62 | 1.63 | 1.63 | 1.64 | 5 |
| 94 | 1.13 | 1.32 | 1.39 | 1.43 | 1.46 | 1.47 | 1.48 | 1.49 | 1.50 | 1.51 | 1.52 | 1.53 | 1.54 | 1.55 | 1.55 | 6 |
| 93 | - | 1.29 | 1.35 | 1.38 | 1.40 | 1.41 | 1.42 | 1.43 | 1.44 | 1.44 | 1.45 | 1.46 | 1.46 | 1.47 | 1.47 | 7 |
| 92 | 1.12 | 1.26 | 1.31 | 1.33 | 1.35 | 1.36 | 1.36 | 1.37 | 1.37 | 1.38 | 1.39 | 1.39 | 1.40 | 1.40 | 1.40 | 8 |
| 91 | 1.11 | 1.23 | 1.27 | 1.29 | 1.30 | 1.30 | 1.31 | 1.31 | 1.32 | 1.32 | 1.33 | 1.33 | 1.33 | 1.34 | 1.34 | 9 |
| 90 | 1.10 | 1.20 | 1.23 | 1.24 | 1.25 | 1.25 | 1.26 | 1.26 | 1.26 | 1.27 | 1.27 | 1.27 | 1.28 | 1.28 | 1.28 | 10 |
| 89 | 1.09 | 1.17 | 1.19 | 1.20 | 1.20 | 1.21 | 1.21 | 1.21 | 1.21 | 1.22 | 1.22 | 1.22 | 1.22 | 1.22 | 1.23 | 11 |
| 88 | 1.07 | 1.14 | 1.15 | 1.16 | 1.16 | 1.16 | 1.16 | 1.17 | 1.17 | 1.17 | 1.17 | 1.17 | 1.17 | 1.17 | 1.17 | 12 |
| 87 | 1.06 | 1.11 | 1.12 | 1.12 | 1.12 | 1.12 | 1.12 | 1.12 | 1.12 | 1.12 | 1.12 | 1.12 | 1.12 | 1.13 | 1.13 | 13 |
| 86 | 1.04 | 1.08 | 1.08 | 1.08 | 1.08 | 1.08 | 1.08 | 1.08 | 1.08 | 1.08 | 1.08 | 1.08 | 1.08 | 1.08 | 1.08 | 14 |
| 85 | 1.03 | 1.05 | 1.05 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 15 |
| 84 | 1.01 | 1.02 | 1.01 | 1.01 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 0.99 | 0.99 | 16 |
| 83 | 1.00 | 0.99 | 0.98 | 0.97 | 0.97 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.95 | 0.95 | 0.95 | 17 |
| 82 | 0.97 | 0.96 | 0.95 | 0.94 | 0.93 | 0.93 | 0.93 | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 18 |
| 81 | 0.96 | 0.93 | 0.91 | 0.90 | 0.90 | 0.89 | 0.89 | 0.89 | 0.89 | 0.88 | 0.88 | 0.88 | 0.88 | 0.88 | 0.88 | 19 |
| 80 | 0.93 | 0.90 | 0.88 | 0.87 | 0.86 | 0.86 | 0.86 | 0.85 | 0.85 | 0.85 | 0.85 | 0.84 | 0.84 | 0.84 | 0.84 | 20 |
| 79 | 0.91 | 0.87 | 0.85 | 0.84 | 0.83 | 0.82 | 0.82 | 0.82 | 0.82 | 0.81 | 0.81 | 0.81 | 0.81 | 0.81 | 0.81 | 21 |
| 78 | 0.89 | 0.84 | 0.82 | 0.80 | 0.80 | 0.79 | 0.79 | 0.79 | 0.78 | 0.78 | 0.78 | 0.78 | 0.77 | 0.77 | 0.77 | 22 |
| 77 | 0.87 | 0.81 | 0.78 | 0.77 | 0.76 | 0.76 | 0.76 | 0.75 | 0.75 | 0.75 | 0.75 | 0.74 | 0.74 | 0.74 | 0.74 | 23 |
| 76 | 0.84 | 0.78 | 0.75 | 0.74 | 0.73 | 0.73 | 0.72 | 0.72 | 0.72 | 0.71 | 0.71 | 0.71 | 0.71 | 0.71 | 0.71 | 24 |
| 75 | 0.82 | 0.75 | 0.72 | 0.71 | 0.70 | 0.70 | 0.69 | 0.69 | 0.69 | 0.68 | 0.68 | 0.68 | 0.68 | 0.68 | 0.67 | 25 |
| 74 | 0.79 | 0.72 | 0.69 | 0.68 | 0.67 | 0.66 | 0.66 | 0.66 | 0.66 | 0.65 | 0.65 | 0.65 | 0.65 | 0.64 | 0.64 | 26 |
Table 1B: Specification Conformity Standard Deviation Method
| Upper Quality Index QU or Lower Quality Index QL | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PU or PL percent within limits for positive values of QU or QL | n=3 | n=4 | n=5 | n=6 | n=7 | n=8 | n=9 | n=10 to n=11 | n=12 to n=14 | n=15 to n=18 | n=19 to n=25 | n=26 to n=37 | n=38 to n=69 | n=70 to n=200 | n=201 to n=inf | PU or PL percent within limits for negative values of QU or QL |
| 73 | 0.76 | 0.69 | 0.66 | 0.65 | 0.64 | 0.63 | 0.63 | 0.63 | 0.62 | 0.62 | 0.62 | 0.62 | 0.62 | 0.61 | 0.61 | 27 |
| 72 | 0.74 | 0.66 | 0.63 | 0.62 | 0.61 | 0.60 | 0.60 | 0.60 | 0.59 | 0.59 | 0.59 | 0.59 | 0.59 | 0.58 | 0.58 | 28 |
| 71 | 0.71 | 0.63 | 0.60 | 0.59 | 0.58 | 0.57 | 0.57 | 0.57 | 0.57 | 0.56 | 0.56 | 0.56 | 0.56 | 0.55 | 0.55 | 29 |
| 70 | 0.68 | 0.60 | 0.57 | 0.56 | 0.55 | 0.55 | 0.54 | 0.54 | 0.54 | 0.53 | 0.53 | 0.53 | 0.53 | 0.53 | 0.52 | 30 |
| 69 | 0.65 | 0.57 | 0.54 | 0.53 | 0.52 | 0.52 | 0.51 | 0.51 | 0.51 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 31 |
| 68 | 0.62 | 0.54 | 0.51 | 0.50 | 0.49 | 0.49 | 0.48 | 0.48 | 0.48 | 0.48 | 0.47 | 0.47 | 0.47 | 0.47 | 0.47 | 32 |
| 67 | 0.59 | 0.51 | 0.47 | 0.47 | 0.46 | 0.46 | 0.46 | 0.45 | 0.45 | 0.45 | 0.45 | 0.44 | 0.44 | 0.44 | 0.44 | 33 |
| 66 | 0.56 | 0.48 | 0.45 | 0.44 | 0.44 | 0.43 | 0.43 | 0.43 | 0.42 | 0.42 | 0.42 | 0.42 | 0.41 | 0.41 | 0.41 | 34 |
| 65 | 0.52 | 0.45 | 0.43 | 0.41 | 0.41 | 0.40 | 0.40 | 0.40 | 0.40 | 0.39 | 0.39 | 0.39 | 0.39 | 0.39 | 0.39 | 35 |
| 64 | 0.49 | 0.42 | 0.40 | 0.39 | 0.38 | 0.38 | 0.37 | 0.37 | 0.37 | 0.36 | 0.36 | 0.36 | 0.36 | 0.36 | 0.36 | 36 |
| 63 | 0.46 | 0.39 | 0.37 | 0.36 | 0.35 | 0.35 | 0.35 | 0.34 | 0.34 | 0.34 | 0.34 | 0.34 | 0.33 | 0.33 | 0.33 | 37 |
| 62 | 0.43 | 0.36 | 0.34 | 0.33 | 0.32 | 0.32 | 0.32 | 0.32 | 0.31 | .031 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 | 38 |
| 61 | 0.39 | 0.33 | 0.31 | 0.30 | 0.30 | 0.29 | 0.29 | 0.29 | 0.29 | 0.29 | 0.28 | 0.28 | 0.28 | 0.28 | 0.28 | 39 |
| 60 | 0.36 | 0.30 | 0.28 | 0.27 | 0.27 | 0.27 | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 | 0.25 | 0.25 | 40 |
| 59 | 0.32 | 0.27 | 0.25 | 0.25 | 0.24 | 0.24 | 0.24 | 0.24 | 0.23 | 0.23 | 0.23 | 0.23 | 0.23 | 0.23 | 0.23 | 41 |
| 58 | 0.29 | 0.24 | 0.23 | 0.22 | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 42 |
| 57 | 0.25 | 0.21 | 0.20 | 0.19 | 0.19 | 0.19 | 0.18 | 0.18 | 0.18 | 0.18 | 0.18 | 0.18 | 0.18 | 0.18 | 0.18 | 43 |
| 56 | 0.22 | 0.18 | 0.17 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 44 |
| 55 | 0.18 | 0.15 | 0.14 | 0.14 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 45 |
| 54 | 0.14 | 0.12 | 0.11 | 0.11 | 0.11 | 0.11 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 46 |
| 53 | 0.11 | 0.09 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 47 |
| 52 | 0.07 | 0.06 | 0.06 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 48 |
| 51 | 0.04 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.02 | 49 |
| 50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 50 |

