U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number: FHWA-RD-98-156 Date: FEBRUARY 1999 |
Introduction |
|
A final demonstration of the PRS consisted of a comparative analysis of the actual price adjustments awarded to the contractor (using the governing SHA specifications) versus those that would have been assessed if the current PRS approach had governed the projects. Such an analysis provides insight into how much of a change would be typical for SHA’s using the PRS technology. This analysis was based on historical data retrieved from three SHA’s, representing 33 lots from 7 JPCP projects. Table 85 contains more specific information on these projects.
Table 85. Projects investigated for pay adjustment comparisons.
|
State |
Project ID |
County |
Number of Lots |
|---|---|---|---|
|
Kansas |
KS-1 |
Wyandotte |
3 |
|
KS-2 |
Greenwood |
7 |
|
|
KS-3 |
Reno |
5 |
|
|
KS-4a |
Pottawatomie |
2 |
|
|
Wisconsin |
WI-1 |
Clark |
5 |
|
WI-2 |
Clark |
8 |
|
|
Iowa |
IA-1b |
Wapello |
3 |
|
Total Number of Lots |
33 |
||
The required data collected for each pavement lot included:
Some data adjustment was required to resolve inconsistencies between theoretical versus actual sublot and lot identification.
The actual AQC sampling and testing data were used to compute PRS-based lot CPF’s using the following procedure:
Finally, the PRS-based CPF’s were directly compared with the actual pay adjustments made to the contractor on the respective lots. This chapter discusses all aspects of this comparative analysis. Due to the similarities of projects within each SHA, the discussion is divided by State. An overall summary of the combined results from all States is also included.
Kansas Projects |
|
Most of the design- and traffic-related variable inputs required to simulate the Level 1 pay factor curves representing each project were obtained directly from KDOT personnel. Many of the cost-related variables were assumed to be equal to those values used at the Kansas OTA field trial (KS-4). Climatic variable values were obtained from available climatic databases. All assumed items are marked as such. The constant variables defining Kansas projects KS-1, KS-2, and KS-3 are presented in tables 86 through 88, respectively. The constant values defining project KS-4 (the Kansas OTA field trial) are presented in table 54 as part of the OTA Field Trial #3 documentation.
Table 86. Constant inputs defining the KS-1 archived project.
| Project Information | ||
| State | Kansas | |
| County | Wyandotte | |
| District | Shawnee Office | |
| Route | I-635 NB | |
| Design method | AASHTO 93 | |
| Project Type | ||
| Pavement type | Plain, doweled | |
| Road location | Urban, divided | |
| Design life | 20 years | |
| Analysis life | 40 years (assumed) | |
| Overlay life | 10 years (assumed) | |
| Project length | 4.096 km | |
| Number of lanes in one direction | 3 | |
| Lane width | 3.7 m | |
| Joint spacing | 4.8 m | |
| Traffic Information | ||
| Total design ESAL’s | 25,359,615 | |
| Traffic growth factor | 0% (assumed) | |
| Traffic growth method | Simple (assumed) | |
| Materials and Climatic Information | ||
| Annual temperature range | 21.1 ºC (assumed) | |
| Freezing index | 200 degree-days (assumed) | |
| Average annual precipitation | 69.4 cm (assumed) | |
| Annual freeze-thaw cycles in pavement (at a depth of 7.6 cm) | 10 (assumed) | |
| Salt present | Yes (assumed) | |
| Transverse joint sealant type | Preformed compression seal | |
| Slab Support Information | ||
| Base type | Bound drainable base, PCC | |
| Modulus of subgrade reaction | 156 MPa/m | |
| Subgrade soil type | Fine-grained (A-4 to A-7) (assumed) | |
| Presence of longitudinal subdrains | Yes | |
| Load Transfer Information | ||
| Dowel bar diameter | 3.5 cm | |
| Presence of tied PCC shoulder | Yes (assumed) | |
| Cost Information | ||
| Construction bid | $32.29/m2 | |
| Cost of overlay (current) | $10.76/m2 (assumed) | |
| Cost of joint patching (current) | $77.74/m2 (assumed) | |
| Cost of slab replacement (current) | $59.80/m2 (assumed) | |
| Annual interest rate | 6% (assumed) | |
| Annual inflation rate | 3% (assumed) | |
Table 87. Constant inputs defining the KS-2 archived project.
| Project Information | ||
| State | Kansas | |
| County | Greenwood | |
| District | Iola Office | |
| Route | K-96 & U.S. 400 EB | |
| Design method | AASHTO 86 | |
| Project Type | ||
| Pavement type | Plain, doweled | |
| Road location | Rural, undivided | |
| Design life | 20 years | |
| Analysis life | 40 years (assumed) | |
| Overlay life | 10 years (assumed) | |
| Project length | 16.88 km | |
| Number of lanes in one direction | 1 | |
| Lane width | 3.7 m | |
| Joint spacing | 4.8 m | |
| Traffic Information | ||
| Total design ESAL’s | 7,459,260 | |
| Traffic growth factor | 0% (assumed) | |
| Traffic growth method | Simple (assumed) | |
| Materials and Climatic Information | ||
| Annual temperature range | 21.1 ºC (assumed) | |
| Freezing index | 0 degree-days (assumed) | |
| Average annual precipitation | 69.4 cm (assumed) | |
| Annual freeze-thaw cycles in pavement (at a depth of 7.6 cm) | 6 (assumed) | |
| Salt present | Yes (assumed) | |
| Transverse joint sealant type | Preformed compression seal | |
| Slab Support Information | ||
| Base type | Bound drainable base, PCC | |
| Modulus of subgrade reaction | 45 MPa/m | |
| Subgrade soil type | Fine-grained (A-4 to A-7) (assumed) | |
| Presence of longitudinal subdrains | Yes | |
| Load Transfer Information | ||
| Dowel bar diameter | 2.5 cm | |
| Presence of tied PCC shoulder | Yes (assumed) | |
| Cost Information | ||
| Construction bid | $22.90/m2 | |
| Cost of overlay (current) | $10.76/m2 (assumed) | |
| Cost of joint patching (current) | $77.74/m2 (assumed) | |
| Cost of slab replacement (current) | $59.80/m2 (assumed) | |
| Annual interest rate | 6% (assumed) | |
| Annual inflation rate | 3% (assumed) | |
Table 88. Constant inputs defining the KS-3 archived project.
| Project Information | ||
| State | Kansas | |
| County | Reno | |
| Project Type | ||
| Pavement type | Plain, doweled | |
| Road location | Rural, divided | |
| Design life | 20 years | |
| Analysis life | 40 years (assumed) | |
| Overlay life | 10 years (assumed) | |
| Project length | 6.7 km | |
| Number of lanes in one direction | 2 | |
| Lane width | 3.7 m | |
| Joint spacing | 4.8 m | |
| Traffic Information | ||
| Total design ESAL’s | 6,721,450 | |
| Traffic growth factor | 0% (assumed) | |
| Traffic growth method | Simple (assumed) | |
| Materials and Climatic Information | ||
| Annual temperature range | 21.1 ºC (assumed) | |
| Freezing index | 0 degree-days (assumed) | |
| Average annual precipitation | 71.1 cm (assumed) | |
| Annual freeze-thaw cycles in pavement (at a depth of 7.6 cm) | 6 (assumed) | |
| Salt present | Yes (assumed) | |
| Transverse joint sealant type | Preformed compression seal | |
| Slab Support Information | ||
| Base type | PCC-treated | |
| Modulus of subgrade reaction | 54 MPa/m | |
| Subgrade soil type | Fine-grained (A-4 to A-7) (assumed) | |
| Presence of longitudinal subdrains | No | |
| Load Transfer Information | ||
| Dowel bar diameter | 3.2 cm | |
| Presence of tied PCC shoulder | Yes (assumed) | |
| Cost Information | ||
| Construction bid | $33.37/m2 | |
| Cost of overlay (current) | $10.76/m2 (assumed) | |
| Cost of joint patching (current) | $77.74/m2 (assumed) | |
| Cost of slab replacement (current) | $59.80/m2 (assumed) | |
| Annual interest rate | 6% (assumed) | |
| Annual inflation rate | 3% (assumed) | |
Appropriate AQC target values were determined for each project by interpreting the Kansas construction specification. The specification was interpreted in accordance with the guidelines set forth in chapter 5 of volume I (Selection of AQC Target Values). The chosen AQC target means and standard deviations used to define the agency-desired quality for projects KS-1, KS-2, and KS-3 are summarized in tables 89 through 91. The AQC target means and standard deviations chosen for project KS-4 (the Kansas OTA field trial) are presented in table 56 as part of the OTA Field Trial #3 documentation.
| Acceptance Quality Characteristic |
Target Mean |
Target Standard Deviation |
|---|---|---|
| 28-day compressive strength, MPa |
24.8 |
3.6 |
| Slab thickness, mm |
279 |
4 |
| Entrained air content, percent |
6.0 |
0.75 |
| Initial smoothness, mm/km (0.0-mm blanking band) |
379 |
47 |
Note: Computed from individual tests (no averaging is performed); thus, it includes both materials/process and testing measurement variation.
| Acceptance Quality Characteristic |
Target Mean |
Target Standard Deviation |
|---|---|---|
| 28-day compressive strength, MPa |
24.8 |
3.4 |
| Slab thickness, mm |
229 |
4 |
| Entrained air content, percent |
6.0 |
0.75 |
| Initial smoothness, mm/km (0.0-mm blanking band) |
379 |
47 |
Note: Computed from individual tests (no averaging is performed); thus, it includes both materials/process and testing measurement variation.
| Acceptance Quality Characteristic |
Target Mean |
Target Standard Deviation |
|---|---|---|
| 28-day compressive strength, MPa |
31.5 |
3.4 |
| Slab thickness, mm |
254 |
4 |
| Entrained air content, percent |
6.0 |
0.75 |
| Initial smoothness, mm/km (0.0-mm blanking band) |
379 |
47 |
Note: Computed from individual tests (no averaging is performed); thus, it includes both materials/process and testing measurement variation.
Retrieval of Actual AQC Sampling and Testing Data
Actual AQC sampling and testing data were retrieved from KDOT historical files for different days of paving at each archived Kansas project. Each day was assumed to be equal to one lot of paving. Archived data were retrieved for concrete strength, slab thickness, and initial smoothness (entrained air content data were not collected since no entrained air content pay adjustments were computed under the actual Kansas construction specifications). All of the test values within each lot were summarized into representative lot means and standard deviations. The lot means and standard deviations were then used to determine representative Level 1 AQC lot pay factors for each respective lot. The as-constructed AQC lot means and standard deviations computed for each Kansas project are summarized in tables 92 through 95.
|
Lot |
28-day Compressive Strength, MPa |
Slab Thickness, mm |
Initial Smoothness, mm/km |
|||
|---|---|---|---|---|---|---|
|
Mean |
Std Dev |
Mean |
Std Dev |
Mean |
Std Dev |
|
|
1 |
25.4 |
0.3 |
296 |
6 |
355 |
45 |
|
2 |
25.9 |
0.5 |
293 |
4 |
209 |
38 |
|
3 |
24.6 |
3.6 1 |
287 |
2 |
313 |
52 |
Note: 1 Only one strength sample was taken within lot 3; therefore, the as-constructed 28-day compressive strength standard deviation was assumed to be equal to the chosen target standard deviation of 3.6 MPa.
|
Lot |
28-day Compressive Strength, MPa |
Slab Thickness, mm |
Initial Smoothness, mm/km |
|||
|---|---|---|---|---|---|---|
|
Mean |
Std Dev |
Mean |
Std Dev |
Mean |
Std Dev |
|
|
1 |
36.1 |
1.4 |
242 |
6 |
195 |
41 |
|
2 |
33.0 |
7.4 |
234 |
7 |
158 |
69 |
|
3 |
35.2 |
0.1 |
238 |
7 |
183 |
34 |
|
4 |
35.4 |
0.3 |
236 |
9 |
179 |
28 |
|
5 |
36.5 |
1.4 |
239 |
5 |
195 |
67 |
|
6 |
35.1 |
2.2 |
231 |
4 |
217 |
33 |
|
7 |
35.3 |
0.0 |
233 |
4 |
218 |
47 |
|
Lot |
28-day Compressive Strength, MPa |
Slab Thickness, mm |
Initial Smoothness, mm/km |
|||
|---|---|---|---|---|---|---|
|
Mean |
Std Dev |
Mean |
Std Dev |
Mean |
Std Dev |
|
|
1 |
37.3 |
3.4 |
260 |
5 |
63 |
12 |
|
2 |
41.3 |
2.9 |
261 |
4 |
52 |
18 |
|
3 |
43.8 |
4.8 |
259 |
3 |
74 |
19 |
|
4 |
43.8 |
5.9 |
256 |
5 |
37 |
17 |
|
5 |
49.0 |
3.6 |
257 |
4 |
44 |
17 |
|
Lot |
28-day Compressive Strength, MPa |
Slab Thickness, mm |
Initial Smoothness, mm/km |
|||
|---|---|---|---|---|---|---|
|
Mean |
Std Dev |
Mean |
Std Dev |
Mean |
Std Dev |
|
|
1 |
37.4 |
1.6 |
208 |
14 |
211 |
27 |
|
2 |
39.1 |
3.1 |
213 |
16 |
186 |
55 |
Simulation
of Level 1 AQC Pay Factor Charts and Equations
Independent AQC Level 1 pay factor charts were simulated for each project based on the respective identified constant variable values and AQC target values. Based on the typical daily amount of AQC sampling and testing observed in the historical records, it was decided that PRS-based pay adjustments for projects KS-1, KS-2, and KS-3 would be most realistic if the pay factor equations were developed for the case of five sublots per lot and three samples per sublot. PRS-based pay equations for project KS-4 were developed for the case of three sublots per lot, and two samples per sublot (this was the sampling frequency used at the field trial).
Each simulated LCC (used to construct the AQC pay factor curves) was determined as the mean of 500 simulated lot LCC’s—using a 40-year analysis life (two times the 20-year design life) and including 5 percent of the calculated user costs. The simulated representative as-designed LCC means for each of the four Kansas projects were simulated as the following :
Pay factor curves for each Kansas project were calculated for different chosen AQC standard deviations, over reasonable ranges of AQC means. The simulated AQC pay factor curves representing Kansas projects KS-1, KS-2, and KS-3 are presented in figures 26 through 28, respectively. The corresponding pay factor regression equations for these three projects are presented in tables 96 through 98, respectively. The pay factor curves and regression equations for the KS-4 project are presented as part of the OTA Field Trial #3 documentation in figure 12 and table 62, respectively.
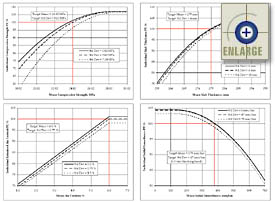 |
Figure 26. Level 1 individual AQC pay factor charts for archived project KS-1 (five sublots, three samples per sublot). |
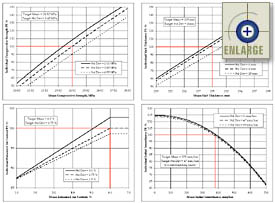 |
Figure 27. Level 1 individual AQC pay factor charts for archived project KS-2 (five sublots, three samples per sublot). |
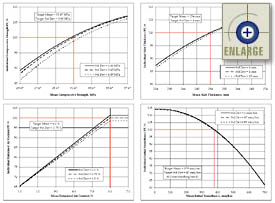 |
Figure 28. Level 1 individual AQC pay factor charts for archived project KS-3 (five sublots, three samples per sublot). |
| Acceptance Quality Characteristic |
As-Constructed Standard Deviation |
Pay Factor Regression Equation, x = mean value |
Maximum Pay Factor, % |
x-Value at Maximum Pay Factor |
|---|---|---|---|---|
| 28-day Cylinder Compressive Strength |
0.0 MPa |
PFS-(x, 0.0) = –0.3049x2 + 17.8047x – 152.8772 |
107.04 |
29.2 MPa |
|
3.6 MPa |
PFS-(x, 3.6) = –0.3438x2 + 20.1499x – 188.3132 |
106.90 |
29.3 MPa |
|
|
7.3 MPa |
PFS-(x, 7.3) = –0.4194x2 + 24.9301x – 264.0556 |
106.46 |
29.7 MPa |
|
| Slab Thickness |
0 mm |
PFT-(x, 0) = –2.6949E-02x2 + 15.7459x – 2195.2267 |
104.77 |
292 mm |
|
4 mm |
PFT-(x, 4) = –2.7817E-02x2 + 16.2580x – 2270.9400 |
104.58 |
292 mm |
|
|
13 mm |
PFT-(x, 13) = –2.8796E-02x2 + 16.8605x – 2363.7344 |
104.33 |
293 mm |
|
| Plastic Entrained Air Content |
0.00% |
PFA-(x, 0.00) = 6.09x + 64.56 |
101.10 |
6.0% |
|
0.75% |
PFA-(x, 0.75) = 6.11x + 63.34 |
100.00 |
6.0% |
|
|
1.50% |
PFA-(x, 1.50) = 5.9167x + 62.7298 |
98.23 |
6.0% |
|
| Initial Smoothness (0.0-mm blanking band) |
0 mm/km |
PFSM-(x, 0) = –7.0189E-05x2 + 1.8403E-02x + 103.20 |
104.41 |
131 mm/km |
|
47 mm/km |
PFSM-(x, 47) = –7.0189E-05x2 + 1.8403E-02x + 103.10 |
104.31 |
131 mm/km |
|
|
79 mm/km |
PFSM-(x, 79) = –7.0189E-05x2 + 1.8403E-02x + 101.94 |
103.15 |
131 mm/km |
Note: The pay factors are held equal to the equation’s maximum pay factor value when the measured value surpasses the corresponding "x-Value at Maximum Pay Factor" (i.e., greater than the corresponding value for strength, thickness, and entrained air content; less than the corresponding value for initial smoothness).
| Acceptance Quality Characteristic |
As-Constructed Standard Deviation |
Pay Factor Regression Equation, x = mean value |
Maximum Pay Factor, % |
x-Value at Maximum Pay Factor |
|---|---|---|---|---|
| 28-day Cylinder Compressive Strength |
0.0 MPa |
PFS-(x, 0.0) = –0.2752x2 + 26.2980x – 374.9736 |
n/a |
n/a |
|
3.4 MPa |
PFS-(x, 3.4) = –0.1583x2 + 20.4789x – 310.7396 |
n/a |
n/a |
|
|
6.9 MPa |
PFS-(x, 6.9) = –0.0730x2 + 15.7397x – 255.6552 |
n/a |
n/a |
|
| Slab Thickness |
0 mm |
PFT-(x, 0) = –1.0182E-02x2 + 9.0643x – 1436.8200 |
n/a |
n/a |
|
4 mm |
PFT-(x, 4) = –5.1116E-03x2 + 6.7336x – 1172.1800 |
n/a |
n/a |
|
|
13 mm |
PFT-(x, 13) = 4.3262E-03x2 + 2.1927x – 636.3400 |
n/a |
n/a |
|
| Plastic Entrained Air Content |
0.00% |
PFA-(x, 0.00) = 3.0333x + 84.5002 |
102.70 |
6.0% |
|
0.75% |
PFA-(x, 0.75) = 2.5333x + 84.002 |
100.00 |
6.0% |
|
|
1.50% |
PFA-(x, 1.50) = 2.2667x + 84.9998 |
98.60 |
6.0% |
|
| Initial Smoothness (0.0-mm blanking band) |
0 mm/km |
PFSM-(x, 0) = –1.17E-04x2 + 7.7294E-03x + 114.60 |
114.73 |
33 mm/km |
|
47 mm/km |
PFSM-(x, 47) = –1.17E-04x2 + 7.7294E-03x + 113.86 |
113.99 |
33 mm/km |
|
|
95 mm/km |
PFSM-(x, 95) = –1.17E-04x2 + 7.7294E-03x + 113.12 |
113.25 |
33 mm/km |
Note: The entrained air content pay factors are held equal to the equation’s maximum pay factor value when the measured mean is greater than the "x-Value at Maximum Pay Factor" value for entrained air content. The initial smoothness pay factors are held equal to the equation’s maximum pay factor value when the measured mean is less than the corresponding "x-Value at Maximum Pay Factor" value for initial smoothness.
| Acceptance Quality Characteristic |
As-Constructed Standard Deviation |
Pay Factor Regression Equation, x = mean value |
Maximum Pay Factor, % |
x-Value at Maximum Pay Factor |
|---|---|---|---|---|
| 28-day Cylinder Compressive Strength |
0.0 MPa |
PFS-(x, 0.0) = –6.5198E-02x2 + 5.5980x – 11.1427 |
109.02 |
42.9 MPa |
|
3.4 MPa |
PFS-(x, 3.4) = –6.8682E-02x2 + 5.8739x – 16.8399 |
108.75 |
42.8 MPa |
|
|
6.9 MPa |
PFS-(x, 6.9) = –7.5821E-02x2 + 6.4527x – 29.1986 |
108.09 |
42.6 MPa |
|
| Slab Thickness |
0 mm |
PFT-(x, 0) = –6.9819E-03x2 + 4.0442x – 476.7190 |
108.92 |
290 mm |
|
4 mm |
PFT-(x, 4) = –6.9819E-03x2 + 4.0430x – 476.5964 |
108.85 |
290 mm |
|
|
13 mm |
PFT-(x, 13) = –7.3057E-03x2 + 4.2301x – 503.6188 |
108.69 |
290 mm |
|
| Plastic Entrained Air Content |
0.00% |
PFA-(x, 0.00) = 7.2067x + 58.1098 |
101.35 |
6.0% |
|
0.75% |
PFA-(x, 0.75) = 6.9850x + 58.0900 |
100.00 |
6.0% |
|
|
1.50% |
PFA-(x, 1.50) = 6.6471x + 58.5336 |
98.42 |
6.0% |
|
| Initial Smoothness (0.0-mm blanking band) |
0 mm/km |
PFSM-(x, 0) = –1.1818E-04x2 + 8.0542E-03x + 114.0875 |
114.22 |
34 mm/km |
|
47 mm/km |
PFSM-(x, 47) = –1.1818E-04x2 + 8.0542E-03x + 113.9050 |
114.04 |
34 mm/km |
|
|
95 mm/km |
PFSM-(x, 95) = –1.1818E-04x2 + 8.0542E-03x + 113.5488 |
113.69 |
34 mm/km |
Note: The pay factors are held equal to the equation’s maximum pay factor value when the measured value surpasses the corresponding "x-Value at Maximum Pay Factor" (i.e., greater than the corresponding value for strength, thickness, and entrained air content; less than the corresponding value for initial smoothness).
Calculation of Pay Adjustments
Lot pay factors were calculated for all of the Kansas projects based on the computed representative AQC lot means and standard deviations. These values were used to compute pay factors using two different calculation methods—using the actual Kansas governing construction specification and using the developed Level 1 PRS pay factor equations. The details of both pay factor calculation methods are described separately below.
Calculation of Pay Adjustments Using the Governing Kansas Construction Specification
For three of the projects (KS-1, KS-2, and KS-3), the governing Kansas construction specification applied pay adjustments to concrete strength, slab thickness, and initial smoothness (no pay adjustments were based on air content). For the KS-4 project, pay adjustments were only applied to slab thickness and initial smoothness. Individual concrete strength and slab thickness pay factors were determined based on the computed lot AQC means and standard deviations of the retrieved AQC testing data. Although initial smoothness pay factors could have been determined from the retrieved field data, the actual initial smoothness-related pay adjustment values (in dollars) were provided by KDOT personnel. All of the details of the pay adjustment procedures included in the governing Kansas construction specification are discussed below.
Individual Concrete Strength (28-day Compressive) Pay Adjustments
Pay adjustments for concrete strength are addressed in section 11.0, Basis of Payment, of the Kansas QC/QA specification. This concrete strength acceptance procedure is discussed in detail in the OTA Field Trial #3 documentation (see the section titled Concrete Strength in chapter 3). The concrete strength pay adjustment procedure is based on determining a compressive strength quality index (QSTR) using equation 34. The computed QSTR is used to select the appropriate compressive strength pay adjustment factor (PSTR) from table 55.
As an example, let us look at lot 1 from the KS-1 project. For this lot, the representative lot mean and standard deviation (obtained from lot sample test values) were computed to be 25.4 and 0.3 MPa, respectively. Since the LSL for the KS-1 project was given as 20.0 MPa, the corresponding QSTR can be calculated as the following using equation 34:
QSTR = (XSTR – LSLSTR) / SSTR
= (25.4 – 20.0) / 0.3
= 18.00
This computed QSTR of 18.00 is translated into a PSTR of 103 percent using the pay schedule presented in table 55.
Individual Slab Thickness Pay Adjustments
Payment for slab thickness is also addressed in section 11.0, Basis of Payment, of the Kansas QC/QA specification. This slab thickness acceptance procedure is discussed in detail in the OTA Field Trial #3 documentation (see the section titled Slab Thickness in chapter 3). The concrete strength pay adjustment procedure is based on determining a slab thickness quality index (QTHK) using equation 35. The computed QTHK is used to select the appropriate compressive strength pay adjustment factor (PTHK) from table 55.
Again, Lot 1 from the KS-1 archived project will be used as an example. For this particular lot, the representative slab thickness lot mean and standard deviation (obtained from lot sample values) were computed to be 296 and 6 mm, respectively. The design slab thickness for this lot was chosen to be 279 mm; therefore, the LSLTHK was calculated to be 5 mm less than the design thickness, or 274 mm. The corresponding QTHK value was then calculated to be the following using equation 35.
QTHK = (XTHK – LSLTHK) / STHK
= (296 – 274) / 6
= 3.67
This computed QTHK of 3.67 is translated into a PTHK of 103 percent using the pay schedule presented in table 55.
Calculation of the Strength/Thickness Composite Pay Adjustments
Using the Kansas QC/QA specification, a combined strength/thickness composite pay factor is calculated for each lot as a function of the independently determined PSTR and PTHK. This composite pay factor (CPFSTR/THK) is computed using equation 46 and rounded to the nearest hundredth (0.01).
CPFSTR/THK = (PSTR * PTHK) / 100 (46)
where
CPFSTR/THK = Strength/thickness composite pay factor.
PSTR = Compressive strength pay adjustment factor.
PTHK = Slab thickness pay adjustment factor.
For our example, the independent concrete strength and slab thickness pay factors were both calculated to be 103 percent (PSTR = PTHK = 103). Therefore, the composite strength/thickness pay factor was calculated (using equation 46) as the following:
CPFSTR/THK = (PSTR * PTHK) / 100
= (103 * 103) / 100
= 106.09 percent
Initial Smoothness Pay Adjustments
Pay adjustments for initial smoothness were addressed in section 502 of a 1990 Kansas DOT special provision to the standard construction specifications. This initial smoothness acceptance procedure is discussed in detail in the OTA Field Trial #3 documentation (see the section titled Initial Smoothness in chapter 3). Under this special provision, pavement smoothness was measured on each 0.16-km section using a California profilograph. The data were then reduced using a 0.0-mm blanking band. Pay adjustments were independently determined for each 0.16-km section.
The actual pay adjustment data (in actual dollars) was provided for each 0.16-km section included at each of the four Kansas projects. A total pay adjustment for each included lot was determined by summing all of the pay adjustments computed for the 0.16-km sections included in each of the defined lots. For our example lot, the initial smoothness lot pay adjustment was computed to be $0.00 (i.e., for this pavement lot, the contractor achieved an average pay factor of 100 percent).
Summary of Pay Adjustments Using the Governing Kansas Construction Specification
A summary of the lot pay factors and pay adjustments calculated using the actual governing KDOT construction specification is presented in tables 99 through 101. Table 99 contains a summary of the concrete strength pay factor calculations. Table 100 contains a summary of the slab thickness pay factor calculations. Table 101 contains a summary of all of the AQC pay factors and adjustments (determined for all of the Kansas projects) using the governing Kansas construction specifications.
|
Project |
Lot 1 |
Total Number of Samples in the Lot |
Computed Lot 28-day Compressive Strength Mean, MPa |
Computed Lot 28-day Compressive Strength Standard Deviation, MPa |
Lower Spe-cification Limit (LSL), MPa |
Computed Strength Quality Index (QSTR) |
Computed Strength Pay Factor (PSTR ), % |
|---|---|---|---|---|---|---|---|
|
KS-1 |
1 |
2 |
25.4 |
0.3 |
20.0 |
18.00 |
103.00 |
|
2 |
2 |
25.9 |
0.5 |
20.0 |
11.80 |
103.00 |
|
|
3 |
1 |
24.6 |
3.6 |
20.0 |
1.28 |
100.00 |
|
|
KS-2 |
1 |
2 |
36.1 |
1.4 |
20.0 |
11.50 |
103.00 |
|
2 |
2 |
33.0 |
7.4 |
20.0 |
1.76 |
103.00 |
|
|
3 |
2 |
35.2 |
0.1 |
20.0 |
152.00 |
103.00 |
|
|
4 |
2 |
35.4 |
0.3 |
20.0 |
51.33 |
103.00 |
|
|
5 |
2 |
36.5 |
1.4 |
20.0 |
11.79 |
103.00 |
|
|
6 |
4 |
35.1 |
2.2 |
20.0 |
6.86 |
103.00 |
|
|
7 |
2 |
35.3 |
0.0 |
20.0 |
— 2 |
103.00 |
|
|
KS-3 |
1 |
5 |
37.3 |
3.4 |
26.9 |
3.06 |
103.00 |
|
2 |
5 |
41.3 |
2.9 |
26.9 |
4.97 |
103.00 |
|
|
3 |
5 |
43.8 |
4.8 |
26.9 |
3.52 |
103.00 |
|
|
4 |
5 |
43.8 |
5.9 |
26.9 |
2.86 |
103.00 |
|
|
5 |
5 |
49.0 |
3.6 |
26.9 |
6.14 |
103.00 |
- Note: 1Compressive strength pay adjustments were not applied on project KS-4.
- 2A strength quality index could not be calculated for this lot due to a measured standard deviation = 0 MPa.
|
Project |
Lot |
Total Number of Samples in the Lot |
Computed Lot Slab Thickness Mean, mm |
Computed Lot Slab Thickness Standard Deviation, mm |
Lower Spe-cification Limit (LSL), mm |
Computed Thickness Quality Index (QTHK) |
Computed Thickness Pay Factor (PTHK ), % |
|---|---|---|---|---|---|---|---|
|
KS-1 |
1 |
5 |
296 |
6 |
274 |
3.67 |
103.00 |
|
2 |
8 |
293 |
4 |
274 |
4.75 |
103.00 |
|
|
3 |
5 |
287 |
2 |
274 |
6.50 |
103.00 |
|
|
KS-2 |
1 |
7 |
242 |
6 |
224 |
3.00 |
103.00 |
|
2 |
12 |
234 |
7 |
224 |
1.29 |
100.00 |
|
|
3 |
9 |
238 |
7 |
224 |
2.00 |
103.00 |
|
|
4 |
9 |
236 |
9 |
224 |
1.33 |
100.00 |
|
|
5 |
11 |
239 |
5 |
224 |
3.00 |
103.00 |
|
|
6 |
11 |
231 |
4 |
224 |
1.75 |
103.00 |
|
|
7 |
10 |
233 |
4 |
224 |
2.25 |
103.00 |
|
|
KS-3 |
1 |
5 |
260 |
5 |
249 |
2.20 |
103.00 |
|
2 |
5 |
261 |
4 |
249 |
3.00 |
103.00 |
|
|
3 |
5 |
259 |
3 |
249 |
3.33 |
103.00 |
|
|
4 |
5 |
256 |
5 |
249 |
1.40 |
100.00 |
|
|
5 |
5 |
257 |
4 |
249 |
2.00 |
103.00 |
|
|
KS-4 |
1 |
4 |
214 |
8 |
198 |
1.95 |
103.00 |
|
2 |
5 |
217 |
14 |
198 |
1.29 |
100.00 |
|
Project |
Lot |
Total Lot Area, m2 |
Bid Price, $/m2 |
Strength Pay Factor (PSTR ), % |
Thickness Pay Factor, (PTHK ), % |
Strength/ Thickness Pay Factor (CPFSTR-THK ), % |
Computed Strength/ Thickness Pay Adjustment, $ |
KDOT Reported Initial Smoothness Pay Adjustment, $ |
Total Lot Pay Adjustment, $ |
Total Project Pay Adjustment, $ |
|---|---|---|---|---|---|---|---|---|---|---|
|
KS-1 |
1 |
4,457 |
32.29 |
103.00 |
103.00 |
106.09 |
8,765 |
0 |
8,765 |
44,008 |
|
2 |
6,850 |
103.00 |
103.00 |
106.09 |
13,469 |
14,872 |
28,341 |
|||
|
3 |
4,770 |
100.00 |
103.00 |
103.00 |
4,621 |
2,281 |
6,902 |
|||
|
KS-2 |
1 |
6,428 |
22.90 |
103.00 |
103.00 |
106.09 |
8,965 |
13,403 |
22,368 |
182,316 |
|
2 |
10,395 |
103.00 |
100.00 |
103.00 |
7,141 |
18,406 |
25,547 |
|||
|
3 |
8,586 |
103.00 |
103.00 |
106.09 |
11,974 |
15,870 |
27,844 |
|||
|
4 |
5,748 |
103.00 |
100.00 |
103.00 |
3,949 |
12,374 |
16,323 |
|||
|
5 |
9,315 |
103.00 |
103.00 |
106.09 |
12,991 |
17,083 |
30,074 |
|||
|
6 |
10,765 |
103.00 |
103.00 |
106.09 |
15,013 |
15,909 |
30,923 |
|||
|
7 |
10,947 |
103.00 |
103.00 |
106.09 |
15,267 |
13,971 |
29,238 |
|||
|
KS-3 |
1 |
7,090 |
33.37 |
103.00 |
103.00 |
106.09 |
14,409 |
10,606 |
25,016 |
175,340 |
|
2 |
6,767 |
103.00 |
103.00 |
106.09 |
13,752 |
13,431 |
27,183 |
|||
|
3 |
10,602 |
103.00 |
103.00 |
106.09 |
21,546 |
14,001 |
35,546 |
|||
|
4 |
11,962 |
103.00 |
100.00 |
103.00 |
11,976 |
28,543 |
40,519 |
|||
|
5 |
10,794 |
103.00 |
103.00 |
106.09 |
21,935 |
25,141 |
47,076 |
|||
|
KS-4 |
1 |
3,897 |
33.49 |
— |
103.00 |
103.00 |
3,915 |
4,558 |
8,373 |
11,991 |
|
2 |
4,629 |
— |
100.00 |
100.00 |
0 |
3,618 |
3,618 |
Note: Pay factors were not applied to strength in the KS-4 project.
Calculation of Pay Adjustments Using the Level 1 PRS Approach
PRS-based pay adjustments were calculated for all of the lots included in the four Kansas projects based on the computed AQC lot means and standard deviations. Each PRS-based lot pay adjustment was computed by using the measured AQC lot mean in the appropriate developed pay factor equations and then interpolating between the results based on the measured AQC lot standard deviation. A detailed explanation of the calculation of PRS Level 1 pay factors for an example lot is contained below.
The measured as-constructed AQC means and standard deviations representing lot 1 of KS-1 were the following:
The pay factor equations presented in table 96 are used to calculate individual AQC pay factors.
Measured As-Constructed Compressive Strength (Mean = 25.4 MPa, Std Dev = 0.3 MPa):
At a mean of 25.4 MPa and a standard deviation of 0.0 MPa:
PFS-(25.4, 0.0) = –0.3049(25.4)2 + 17.8047(25.4) – 152.8772 = 102.65% (47)
At a mean of 25.4 MPa and a standard deviation of 3.6 MPa:
PFS-(25.4, 3.6) = –0.3438(25.4)2 + 20.1499(25.4) – 188.3132 = 101.69% (48)
The pay factor for the case with strength mean and standard deviation equal to 25.4 and 0.3 MPa, respectively, is interpolated (using an assumed linear relationship) by the following equation:
PFS-(25.4, 0.3) = PFS-(25.4, 3.6) + (PFS-(25.4, 0.0) – PFS-(25.4, 3.6)) * [(3.6 MPa – 0.3 MPa) / (3.6 MPa – 0.0 MPa)] (49)
= 101.69% + (102.65% – 101.69%) * [(3.3 MPa) / (3.6 MPa)]
= 102.57%
Measured As-Constructed Thickness (Mean = 296 mm, Std Dev = 6 mm):
At a mean of 296 mm and a standard deviation of 4 mm:
PFT-(296, 4) = –2.7817E-02(296)2 + 16.2580(296) – 2270.94 = 104.21% (50)
At a mean of 296 mm and a standard deviation of 13 mm:
PFT-(296, 13) = –2.8796E-02(296)2 + 16.8605(296) – 2363.7344 = 103.98% (51)
The pay factor for the case with thickness mean and standard deviation equal to 296 and 6 mm, respectively, is interpolated (using an assumed linear relationship) by the following equation:
PFT-(296, 6) = PFT-(296, 13) + (PFT-(296, 4) – PFT-(296, 13)) * [(13 mm – 6 mm) / (13 mm – 4 mm)] (52)
= 103.98% + (104.21% – 103.98%) * [(7 mm)/(9 mm)]
= 104.16%
Measured As-Constructed Initial Smoothness (Mean = 355 mm/km, Std Dev = 45 mm/km):
At a mean of 355 mm/km and a standard deviation of 0 mm/km:
PFSM-(355, 0) = –7.0189E–05(355)2 – 0.1840(355) + 103.2 = 100.89% (53)
At a mean of 355 mm/km and a standard deviation of 47 mm:
PFSM-(355, 47) = –7.0189E–05(355)2 – 0.1840(355) + 103.1 = 100.79% (54)
The pay factor for the case with initial smoothness mean and standard deviation equal to 355 and 45 mm/km, respectively, is interpolated (using an assumed linear relationship) by the following equation:
PFSM-(355, 45) = PFSM-(355, 47) + (PFSM-(355, 0) – PFSM-(355, 47)) * [(47 mm/km – 45 mm/km)/(47 mm/km – 0 mm/km)] (55)
= 100.79% + (100.89% – 100.79%) * [(2 mm/km) / (47 mm/km)]
= 100.79%
Calculation of the PRS Composite Pay Factor and Pay Adjustment
The overall composite pay factor for the example lot is calculated using the product method (i.e., the individual AQC pay factors are multiplied together). This composite pay factor equation is shown in equation 56. Note that the individual AQC pay factors are expressed as decimals in the CPF equation (e.g., a pay factor of 102 percent is expressed as 1.02).
CPFLOT = PFSTRENGTH * PFTHICKNESS * PFSMOOTHNESS (56)
For the Level 1 analysis, it was also decided to apply AQC pay factor limits in a manner similar to those limits applied using the actual Kansas construction specifications. The Kansas QC/QA specification allowed maximum pay factors of 103 percent for concrete strength and slab thickness. Therefore, the maximum composite pay factor for strength/thickness was computed as 1.03 * 1.03 = 1.0609, or a 6.09-percent maximum pay adjustment. In addition to the strength/thickness pay factor, the KDOT specification also allows up to an 8.00-percent pay adjustment for initial smoothness. Therefore, using the Kansas QC/QA specification, the maximum incentive pay adjustment (computed as the sum of the strength/thickness and initial smoothness pay adjustments) is approximately 114 percent. These same pay factor limits were, therefore, used for this analysis.
For the example lot, the composite pay factor is calculated as the following using equation 56. (Note: The thickness pay factor computed to be 1.0416 has been limited to the chosen maximum of 1.03.):
CPFLOT = PFS-(25.4, 0.3) * PFT-(296, 6) * PFSM-(355, 45)
= (1.0257) * (1.0300) * (1.0079) = 1.0648
which translates to an overall pay factor of 106.48 percent.
Overall lot pay adjustments are calculated using equation 57.
PAYLOT = (CPFLOT – 1) * BID * AREALOT (57)
where
PAYLOT = Overall Level 1 PRS lot price adjustment, $.
CPFLOT = Overall lot composite pay factor (expressed as a decimal).
BID = Contractor unit bid price, $/m2.
AREALOT = Total area of the lot, m2.
For the example lot, the unit bid price was $32.29/m2, and the total lot area was 4,457 m2. Therefore, using the computed limited CPFLOT of 1.0648, the overall Level 1 lot price adjustment was computed as the following using equation 57:
PAYLOT = (CPFLOT – 1) * BID * AREALOT
= (1.0648 – 1) * 32.29 * 4,457
= 9,973 dollars
A summary of all the Level 1 PRS pay factors and pay adjustments (calculated for all the lots in the four Kansas projects) is presented in table 102.
|
Project |
Lot |
Total Lot Area, m2 |
Bid Price, $/m2 |
Independent Strength Pay Factor (PSTR), % (103% cap)1 |
Independent Thickness Pay Factor (PTHK), % (103% cap)2 |
Independent Smoothness Pay Factor (PSM), % (108% cap)3 |
Lot Composite Pay Factor (CPFLOT), % (limited to 114.0%)4 |
Total Lot PRS Pay Adjustment (based on limited PF’s), $ |
Total Project PRS Pay Adjustment (based on limited PF’s), $ |
|---|---|---|---|---|---|---|---|---|---|
|
KS-1 |
1 |
4,457 |
32.29 |
102.57 |
103.00 |
100.79 |
106.48 |
9,973 |
43,953 |
|
2 |
6,850 |
103.00 |
103.00 |
104.34 |
110.69 |
23,645 |
|||
|
3 |
4,770 |
99.33 |
103.00 |
104.30 |
106.71 |
10,335 |
|||
|
KS-2 |
1 |
6,428 |
22.90 |
103.00 |
103.00 |
108.00 |
114.00 |
20,608 |
199,362 |
|
2 |
10,395 |
103.00 |
103.00 |
108.00 |
114.00 |
33,326 |
|||
|
3 |
8,586 |
103.00 |
103.00 |
108.00 |
114.00 |
27,527 |
|||
|
4 |
5,748 |
103.00 |
103.00 |
108.00 |
114.00 |
18,428 |
|||
|
5 |
9,315 |
103.00 |
103.00 |
108.00 |
114.00 |
29,864 |
|||
|
6 |
10,765 |
103.00 |
103.00 |
108.00 |
114.00 |
34,513 |
|||
|
7 |
10,947 |
103.00 |
103.00 |
108.00 |
114.00 |
35,096 |
|||
|
KS-3 |
1 |
7,090 |
33.37 |
103.00 |
102.74 |
108.00 |
114.00 |
33,123 |
207,156 |
|
2 |
6,767 |
103.00 |
102.98 |
108.00 |
114.00 |
31,614 |
|||
|
3 |
10,602 |
103.00 |
102.25 |
108.00 |
113.74 |
48,611 |
|||
|
4 |
11,962 |
103.00 |
100.81 |
108.00 |
112.14 |
48,459 |
|||
|
5 |
10,794 |
103.00 |
101.21 |
108.00 |
112.59 |
45,349 |
|||
|
KS-4 |
1 |
3,897 |
33.49 |
103.00 |
101.39 |
107.51 |
112.27 |
16,014 |
37,717 |
|
2 |
4,629 |
103.00 |
103.00 |
108.24 |
114.00 |
21,704 |
- Notes: 1 Independent strength pay factors are capped at a maximum of 103%.
- 2 Independent slab thickness pay factors are capped at a maximum of 103%.
- 3 Independent initial smoothness pay factors are capped at a maximum of 108%.
- 4 Lot CPF’s are computed using the product method (see volume I, chapter 6, for more information on the product CPF method). Lot CPF’s are capped at a maximum of 114%.
|
Comparison of Kansas PRS-Based Pay Adjustments to Actual Pay Adjustments Direct comparisons of the actual pay adjustments computed using the governing KDOT construction specification to those computed using the Level 1 PRS are presented in table 103. Ratios of the Level 1 PRS pay adjustments to the actual pay adjustments are also contained in table 103. For the Kansas projects, the Level 1 lot PRS pay adjustments (capped at a maximum of 114 percent) were generally found to be greater than those determined using the KDOT specification. This trend held true for 12 of the 17 lots investigated. However, there appeared to be fairly large variations in the computed lot ratios, within each project. The average of these lot ratios (within each project) were computed to be the following:
|
|
Project |
Lot |
Pay Adjustments Computed Using the Governing KDOT Construction Specification |
Pay Adjustments Computed Using the Level 1 PRS Method |
Ratio of Computed Level 1 PRS Pay Adjustments to Those Determined Using the Governing KDOT Specification |
|||
|---|---|---|---|---|---|---|---|
|
Total Lot Pay Adjustment, $ |
Total Project Pay Adjustment, $ |
Total Lot Pay Adjustment, $ |
Total Project Pay Adjustment, $ |
Ratio of Lot Pay Adjustments |
Ratio of Project Pay Adjustments |
||
|
KS-1 |
1 |
8,765 |
44,008 |
9,973 |
43,953 |
1.14 |
1.00 |
|
2 |
28,341 |
23,645 |
0.83 |
||||
|
3 |
6,902 |
10,335 |
1.50 |
||||
|
KS-2 |
1 |
22,368 |
182,316 |
20,608 |
199,362 |
0.92 |
1.09 |
|
2 |
25,547 |
33,326 |
1.30 |
||||
|
3 |
27,844 |
27,527 |
0.99 |
||||
|
4 |
16,323 |
18,428 |
1.13 |
||||
|
5 |
30,074 |
29,864 |
0.99 |
||||
|
6 |
30,923 |
34,513 |
1.12 |
||||
|
7 |
29,238 |
35,096 |
1.20 |
||||
|
KS-3 |
1 |
25,016 |
175,340 |
33,123 |
207,156 |
1.32 |
1.18 |
|
2 |
27,183 |
31,614 |
1.16 |
||||
|
3 |
35,546 |
48,611 |
1.37 |
||||
|
4 |
40,519 |
48,459 |
1.20 |
||||
|
5 |
47,076 |
45,349 |
0.96 |
||||
|
KS-4 |
1 |
8,373 |
11,991 |
16,014 |
37,717 |
1.91 |
3.15 |
|
2 |
3,618 |
21,704 |
6.00 |
||||
Note: The Level 1 PRS-based lot pay adjustments were computed using a maximum CPF of 114.0 percent.
Two Wisconsin projects were investigated as part of the pay adjustment study. The two projects were conducted on the same State highway with the same design; however, the design thickness for each was expressed differently. The WI-1 project was specified by the SHA in the traditional English units as 11.00 in (converted to 279 mm), while the design thickness for WI-2 was expressed directly in metric units as 275 mm. Because there was a slight difference in design thickness between the two methods, WI-1 and WI-2 were investigated independently. The details of the investigations of each project are discussed in the following sections. Most of the design- and traffic-related variable inputs required to simulate the WI-1 and WI-2 Level 1 pay factor curves were obtained directly from Wisconsin Department of Transportation (WisDOT) personnel. Most of the climatic variable values were obtained from available climatic databases. All variables that were assumed are marked as such. The constant variables defining both WI-1 and WI-2 are presented in table 104. Table 104. Constant inputs defining the WI-1 and WI-2 archived projects.
Appropriate AQC target values were determined for each project by interpreting the Wisconsin construction specification. The specification was interpreted in accordance with the guidelines set forth in chapter 5 of volume I (Selection of AQC Target Values). The chosen AQC target means and standard deviations used to define the agency-desired quality for projects WI-1 and WI-2 are summarized in tables 105 and 106. Table 105. Level 1 AQC target means and standard deviations for the Wisconsin WI-1 archived project.
Table 106. Level 1 AQC target means and standard deviations for the Wisconsin WI-2 archived project.
Retrieval of Actual AQC Sampling and Testing Data Actual AQC sampling and testing data were retrieved from WisDOT historical files for different days of paving at each archived project. Each day was assumed to be equal to one lot of paving. Archived data were retrieved for concrete strength, slab thickness, and initial smoothness (entrained air content data were not collected since no entrained air content pay adjustments were computed under the actual Wisconsin construction specification). All of the test values within each lot were summarized into representative lot means and standard deviations. The lot means and standard deviations were then used to determine representative Level 1 AQC lot pay factors for each respective lot. The as-constructed AQC lot means and standard deviations computed for each Wisconsin project are summarized in tables 107 and 108.
Simulation of Level 1 AQC Pay Factor Charts and Equations Independent AQC Level 1 pay factor charts were simulated for each project based on the respective identified constant variable values and AQC target values. Based on the typical daily amount of AQC sampling and testing observed in the historical records, it was decided that PRS-based pay adjustments for projects WI-1 and WI-2 would be most realistic if the pay factor equations were developed for the case of four sublots per lot and four samples per sublot. Each simulated LCC (used to construct the AQC pay factor curves) was determined as the mean of 500 simulated lot LCC’s—using a 54-year analysis life (two times the 27-year design life) and including 5 percent of the calculated user costs. The simulated representative as-designed LCC means for each of the two Wisconsin projects were simulated as the following:
Pay factor curves for each Wisconsin project were calculated for different chosen AQC standard deviations, over reasonable ranges of AQC means. The simulated AQC pay factor curves representing projects WI-1 and WI-2 are presented in figures 29 and 30, respectively. The corresponding pay factor regression equations for these two projects are presented in tables 109 and 110, respectively.
Calculation of Pay Adjustments Lot pay adjustments were calculated for the two Wisconsin projects based on the computed representative AQC lot means and standard deviations. These values were used to compute pay factors using two different calculation methods—using the actual Wisconsin governing construction specification and using the developed Level 1 PRS pay factor equations. The details of both pay factor calculation methods are described separately below. Calculation of Pay Adjustments Using the Governing Wisconsin Construction Specification The governing Wisconsin construction specification applied pay adjustments to concrete strength, slab thickness, and initial smoothness (no pay adjustments were based on air content). All of the details of the pay adjustment procedures included in the governing Wisconsin construction specification are discussed below. Individual Concrete Strength (28-day Compressive) Pay Adjustments Unit concrete strength pay adjustments were provided for each lot by WisDOT personnel. Individual lot pay adjustments were computed by multiplying the total volume of concrete in each lot by the provided unit pay adjustment. The total volume of concrete for the lot was computed using equation 58.
where
As an example, let us look at lot 1 from the WI-1 project. For this lot, the concrete strength unit pay adjustment was given as –$1.24/m3. Using the design thickness of 279 mm, a defined lot width of 7.92 m, and the measured lot length of 1,153 m, the total estimated lot volume was calculated as 2,553 m3 using equation 58. The total concrete strength pay adjustment for lot 1 of the WI-1 project was then computed as –$1.24/m3 * 2,553 m3 = –$3,166. Individual Slab Thickness Pay Adjustment Slab thickness pay adjustments were assumed to be applied using the pay factor schedule provided in the draft Wisconsin Quality Management Program (QMP) provisions. This table of thickness-based disincentives is presented in table 111. Table 111. Wisconsin draft QMP slab thickness pay adjustment schedule.
Initial Smoothness Pay Adjustments Pay factors for initial smoothness were computed using the pay schedule presented in table 112. Table 112. Wisconsin concrete pavement smoothness pay factors.
The lot initial smoothness pay adjustments are calculated using equation 59.
where
As an example, lot 1 of project WI-1 had a reported mean profile index of 83 mm/km. The corresponding pay factor for this lot was determined as 102 percent from table 112. For the example lot, the unit bid price was $21.70/m2 and the total lot area was 2,553 m2. Therefore, the overall lot initial smoothness pay adjustment was computed as the following using equation 59:
Summary of Pay Adjustments Using the Governing Wisconsin Construction Specification A summary of the lot pay factors and pay adjustments calculated using the actual governing WisDOT construction specification is presented in table 113. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Calculation of Pay Factors Using the Level 1 PRS Approach PRS-based pay adjustments were calculated for all of the lots included in the two Wisconsin projects based on the computed AQC lot means and standard deviations. Each PRS-based lot pay adjustment was computed by using the measured AQC lot mean in the appropriate developed pay factor equations and then interpolating between the results based on the measured AQC lot standard deviation. A detailed explanation of the calculation of PRS Level 1 pay factors for an example lot is contained below. The measured as-constructed AQC means and standard deviations representing lot 1 of WI-1 were the following:
The pay factor equations presented in table 109 are used to calculate individual AQC pay factors. Measured As-Constructed Compressive Strength (Mean = 26.5 MPa, Std Dev =2.6 MPa): At a mean of 26.5 MPa and a standard deviation of 0.0 MPa:
At a mean of 26.5 MPa and a standard deviation of 3.8 MPa:
The pay factor for the case with strength mean and standard deviation equal to 26.5 and 2.6 MPa, respectively, is interpolated (using an assumed linear relationship) by the following equation:
Measured As-Constructed Thickness (Mean = 288 mm, Std Dev = 6 mm): At a mean of 288 mm and a standard deviation of 5 mm:
At a mean of 296 mm and a standard deviation of 10 mm:
The pay factor for the case with thickness mean and standard deviation equal to 288 and 6 mm, respectively, is interpolated (using an assumed linear relationship) by the following equation:
Measured As-Constructed Initial Smoothness (Mean = 83 mm/km, Std Dev = 20 mm/km): At a mean of 83 mm/km and a standard deviation of 12 mm/km:
At a mean of 83 mm/km and a standard deviation of 79 mm:
The pay factor for the case with initial smoothness mean and standard deviation equal to 83 and 20 mm/km, respectively, is interpolated (using an assumed linear relationship) by the following equation:
Calculation of the PRS Composite Pay Factor and Pay Adjustment The overall composite pay factor for the example lot is calculated using the product method (i.e., the individual AQC pay factors are multiplied together). This composite pay factor equation is shown in equation 56. Note that the individual AQC pay factors are expressed as decimals in the CPF equation (e.g., a pay factor of 102 percent is expressed as 1.02). For the Level 1 analysis, it was decided to apply practical AQC pay factor limits in a manner similar to those limits applied using the actual Wisconsin construction specifications. The concrete strength and slab thickness were limited typical maximum pay factors of 103 percent, while an upper limit of 105 percent was applied for initial smoothness. It is important to note that pay factor limits must be determined by an agency when applying a Level 1 PRS. For the example lot, the composite pay factor is calculated as the following using equation 56. (Note: The thickness pay factor computed to be 1.0309 has been limited to the chosen maximum of 1.03):
which translates to an overall pay factor of 96.63 percent. Overall lot pay adjustments are calculated using equation 57. For the example lot, the unit bid price was $21.70/m2, and the total lot area was 2,553 m2. Therefore, using the computed limited CPFLOT of 0.9663, the overall Level 1 lot price adjustment was computed as the following using equation 57:
A summary of all the Level 1 PRS pay factors and pay adjustments (calculated for both Wisconsin projects) is presented in table 114.
Comparison of Wisconsin PRS-Based Pay Adjustments to Actual Pay Adjustments Direct comparisons of the actual pay adjustments computed using the governing WisDOT construction specification to those computed using the Level 1 PRS are presented in table 115. Ratios of the Level 1 PRS pay adjustments to the actual pay adjustments are also contained in table 115. As with the Kansas projects, the computed pay ratios (Level 1 pay adjustments to actual pay adjustments) for the Wisconsin projects varied greatly within each project.
An analysis of the second Wisconsin project, WI-2, showed that the Level 1 lot PRS pay adjustments were generally found to be greater than those determined using the WisDOT specification. This trend held true for seven of the eight lots investigated. The average lot ratio for this project was computed to be 1.23. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Actual pay adjustment information was obtained for the original Ottumwa, Iowa project described in detail in chapter 2 of this volume. The constant variable inputs defined for this project are presented in table 1. The chosen Level 1 AQC target values are presented in table 5. Pay adjustments were only applied to initial smoothness and slab thickness under the governing Iowa construction specification. All aspects of the pay adjustment analysis of the Ottumwa, Iowa project (IA-1) are contained in the following sections. Retrieval of Actual AQC Sampling and Testing Data Actual AQC sampling and testing data were retrieved from Iowa DOT historical files for different days of paving at the IA-1 project. Each day was assumed to be equal to one lot of paving. Archived data were retrieved for slab thickness and initial smoothness only. All of the test values within each lot were summarized into representative lot means and standard deviations. The lot means and standard deviations were then used to determine representative Level 1 AQC lot pay factors for each respective lot. The as-constructed AQC lot means and standard deviations computed for the IA-1 project are summarized in table 116. Table 116. Computed as-constructed AQC lot means and standard deviations for the Iowa IA-1 project.
Independent AQC Level 1 pay factor charts were simulated for the project based on the respective identified constant variable values and AQC target values. A complete summary of the procedures used to develop these curves for the IA-1 project is contained in the section titled Level 1—Development of Individual AQC Pay Factor Curves and Equations. The IA-1 Level 1 pay factor charts, for the cases of 3 and 4 sublots, are presented in figures 1 and 2, respectively. Corresponding best-fit regression equations for the simulated pay factor curves are contained in table 14. Calculation of Pay Adjustments Lot pay adjustments were calculated for the Iowa project based on the computed representative AQC lot means and standard deviations. These values were used to compute pay factors using the two different calculation methods—using the actual Iowa governing construction specification and using the developed Level 1 PRS pay factor equations. Details of both pay factor calculation methods are described separately below. Calculation of Pay Adjustments Using the Governing Iowa Construction Specification The governing Iowa construction specification applied pay adjustments to slab thickness and initial smoothness only. Slab thickness pay adjustments were computed (using the measured AQC lot data) in accordance with table 3. Initial smoothness pay adjustments were computed in accordance with table 4. A complete discussion of the Iowa acceptance procedures is contained in chapter 2 in the section titled Definition of the Required As-Designed AQC Target Values. A summary of the actual lot pay factors and pay adjustments computed using the governing Iowa DOT construction specification is presented in table 117.
PRS-based pay adjustments were calculated for all of the lots included in the Iowa project based on the computed AQC lot means and standard deviations. Each PRS-based lot pay adjustment was computed by using the measured AQC lot mean in the appropriate developed pay factor equations and then interpolating between the results based on the measured AQC lot standard deviation. A detailed example of the calculation of PRS Level 1 pay factors at the Iowa project is contained in chapter 2 in the section titled Calculation of Shadow Pay Factors. It was decided to apply practical AQC pay factor limits similar to those applied using the actual Iowa construction specifications. The slab thickness pay factor was limited to 103 percent, based on the maximum shown in table 3. The initial smoothness pay factor was limited to 105 percent, based on the payment schedule presented in table 4. A summary of all the Level 1 PRS pay factors and pay adjustments (calculated for the Iowa project) is presented in table 118.
Direct comparisons of the actual pay adjustments computed using the governing Iowa DOT construction specification to those computed using the Level 1 PRS are presented in table 119. Ratios of the Level 1 PRS pay adjustments to the actual pay adjustments are also contained in table 119. An analysis of the lot pay adjustments showed that the lot 1 and lot 2 pay adjustments were similar using the two methods. For those lots, the level 1 PRS pay adjustments were computed to be less than those computed using the governing Iowa specification. For the third lot, a disincentive was computed using the Level 1 PRS approach (due to initial smoothness being of poorer quality than the chosen as-designed target value), whereas the governing specification indicated that no pay adjustment was necessary.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Overall, the comparison of actual pay adjustments (computed using the SHA’s governing specification) to Level 1 PRS pay adjustments showed that the trends can vary greatly from lot to lot. PRS-based pay factors were limited using the actual SHA pay factor limits (when available). A majority of the lots (20 of 33) showed that the Level 1 PRS pay adjustment was greater than that determined using the governing SHA specification. Ratios of PRS-based pay adjustments to actual pay adjustments were computed for each lot and project included in the study. An analysis of the absolute values of these ratios showed overall average lot and project ratios of 1.85 and 1.43, respectively (i.e., on average, lot and project pay adjustments [positive or negative] were 1.85 and 1.43 times larger under PRS). A complete summary of the actual versus PRS pay adjustments (for all 33 lots) is shown in table 120. Figure 31 contains a chart showing the PRS pay adjustments versus the actual pay adjustments (using SHA specifications) for all of the SHA’s. Table 120. Summary of actual pay adjustments to Level 1 PRS-based pay adjustments for all SHA’s.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||