U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-13-054 Date: November 2013 |
Publication Number: FHWA-HRT-13-054 Date: November 2013 |
Motivation
Travel behavior is an important component, and perhaps the most complex factor, contributing to the high complexity of a transportation system. The author's motivation here is to show that it is viable to use a behavior-based ABMS approach to study transportation in a bottom-up manner, rather than using the traditional top-down methods, which lack sufficient understanding of underlying behavioral factors. The shortcoming of a top-down method is in always providing a scenario-specific indicator. A change in the studied scenario usually requires establishing a new top-down method, with appropriate assumption, from scratch. A bottom-up approach has the flexibility to apply in a variant scenario, is capable of predicting the system performance under presently non-existing scenarios, and can possibly observe emergent behavior as a stimulus to a new environment setup. This is because it captures the underlying interacting and evolutionary mechanisms in a complex system. In summary, the traditional top-down approach studies what is the performance of a complex transportation system, whereas the bottom-up ABMS approach tries to understand why travelers make those decisions and how does the transportation system perform in such a circumstance.
Understanding traveler behavior is one of the important studies with respect to the transportation system. Traveler behavior can be divided into two parts: before a trip (pre-planned) and within a trip (en route decisions). The before-trip behavior mainly refers to route choice, and this topic is well studied by the activity-based travel demand models tied with an ABMS (see agent-based transportation platforms in chapter 4). In general, the route choice behavior may change as time elapses, because of the interactions between travelers as well as sudden changes in the transportation network topology and performance (e.g., due to an incident). In addition, travelers' route choice behavior involves learning from previous experiences, heterogeneity of travelers, incomplete network information, and communications among travelers. Those behaviors, which are not viable to model through the conventional equilibrium method or discrete choice models, could be tackled by ABMS. In the next section, the authors use a simple example to demonstrate this route choice model framework, which is implemented in AnyLogic software and tested with two simulation experiments. Results from numeric examples are compared with the classical network equilibrium solutions. The goal is to exhibit how network topology changes can influence the traveler's decisionmaking in an ABMS framework, which could lead to results similar to those of the classical model as reported in the literature. This agent-based model provides an example to show the possibility of studying and understanding the travelers' complex decisionmaking under a wide variety of scenarios.
One traditional benchmark of a traveler's route choice criterion is the user equilibrium (UE) principle, in which a traveler chooses a route so as to minimize his or her travel time, and all used routes have equal and minimal travel time.(163) This behavior at the individual level creates equilibrium at the system (or network) level. Deterministic UE assumes that all travelers are homogeneous, that they have full perception of the network, and that they always choose routes with the lowest cost. Boundedly rational UE assumes travelers have full perception of the network but that they may choose a route with a higher travel time within a boundary.(164) In contrast, Stochastic UE assumes travelers have perception errors and that they make route choice decisions based on their perceived travel time.(165) Discrete choice models are often used to depict the heterogeneity. DTA considers time variations in a traffic network, which assumes that travel times on links vary over time. The UE condition therefore only applies to the same departure time interval between the same O-D pair.(166) This extension could analyze phenomena such as peak-hour congestion or time-varying tolls.(167) In recent years, owing to the continuously increasing computer power, researchers have been able to simulate an individual traveler's behavior in a large transportation network. Such applications include MIcroscopic Traffic SIMulator (MITSIM),(168) DYNASMART,(169) and DynusT,(91) in which either microscopic or mesoscopic simulators are embedded. Those studies focus more on how the travelers make their decisions rather than why the travelers make such decisions.
Although disaggregated travel demand models and microscopic traffic simulation models have been applied to modeling the route choice behavior in an integrated simulation environment,(167-168) it is difficult to model the information-sharing among travelers, the interactions among travelers, and the changes to the transportation network by using traditional non-agent based modeling schemes. Agent-based modeling was specifically developed to address this complexity and to support individual decisionmaking. ABMS has been widely implemented in many areas; however, as discussed in chapter 5, those studies with the subject termed as MAS come mainly under the umbrella of the computational method of AI and DAI. Differentiating from those studies, ABMS demonstrated in this chapter explicitly models individual-based traveler's route choice behaviors, with an emphasis on the capability of the effects of learning and interaction.
In summary, the strengths and benefits of integrating ABMS to study travelers' route choice behavior, rather than the traditional route choice models, include the ability to:
An Example Applying ABMS Model to Route Choice Behavior Model
Travelers are modeled as agents, who choose a route based on their knowledge of the network prior to each trip (en route choice is not considered in this example). In the route choice model, a traveler agent first decides which route to travel when their trip starts. The traveler could decide to stay on the same route as the previous trip or could decide to change to an alternative route. At first, the traveler may have little or no information about which is the best route, but experience can help the traveler find his or her best route. In this example, best is based on travel time. Travelers might not have sufficient incentive to change routes if their experienced travel time is close enough to their perceived minimum travel time. If, however, they experience a travel time that is sufficiently different from their expectation, they will consider changing routes.
The following rules are developed to mimic the behavior of an agent who is considering a route change. Suppose TTnj is the experienced travel time of jth route on nth day (that means a traveler agent chooses route j on the nth day) and is the traveler's perceived minimum travel time on the nth day. It is reasonable to assume that a traveler agent may know the travel time only for the route he or she has experienced; thus, the perceived minimum travel time may not be the actual minimum travel time. An initial travel time, which reflects the agent's expectation of each route, is assigned to every traveler agent before the first trip. If the travel time of a route is not observed in a certain trip, the traveler agent uses previously experienced travel times of the route or the initial travel time if the route has never been chosen before, to determine TTnmin. The traveler agent updates the travel time only for the selected routes, while leaving those of other routes unchanged. These rules are stated as follows:
RULE 1: If (TTnj = TTnmin), then the traveler agent does not change route on n + 1th day.
RULE 2: If (TTnj - TTnmin) ≤ ε, then the traveler agent does not change route on n + 1th day, where ε is a threshold related to the perception error.
RULE 3: If (TTnj - TTnmin) > ε, then the traveler agent changes route with probability (TTnj - TTnmin) / TTnj and the choice probability is based on the posterior probability given the route choice and previously experienced travel time.
RULE 1 represents the case when traveler agents are already travelling on the route that corresponds to their perceived minimum travel time; hence, they do not change routes. RULE 2 represents the case when the travel time of the current route is very close to the perceived minimum travel time; hence, the traveler agents will maintain their original choice. RULE 3 represents the situation when traveler agents might change their routes, and the route change probability is related to the difference between the experienced travel time and the perceived minimum travel time. The larger the difference, the higher the route changes probability.
When a traveler agent decides to change routes, a decision must be made on which route to choose. This primer considers the learning process of an agent and the heterogeneity of different travelers.
The learning process details how agents make route choice decisions based on their previous experiences. It can be characterized as Bayesian learning.(170) For each traveler agent, the prior probability represents the subjective probability (traveler's belief) that one route takes the minimum travel time. Data is based on the experience of the traveler and the perceived minimum travel time. The corresponding posterior subjective probability is updated based on the prior subjective probability and the data.
For each O-D pair, suppose pjn denotes the subjective probability that the jth route takes the minimum travel time on the nth day and pn denotes the vector of subjective probabilities. djn is a data variable that equals 1 if the traveler perceives that the jth route takes the minimum travel time (TTnmin) on the nth day, and 0 otherwise. dn is the vector of minimum travel time variables. Based on Bayes' theorem, the posterior distribution can be expressed as:
f pn+1 f(pn|dn) ∝ g(dn|pn)f(pn) (1)
The route choice given the subjective probability g(dn|pn) follows a multinomial distribution with trial number one. The probability mass function of dn is:
g(dn|pn) = ∏j∈J pjnd jn (2)
where j is the total number of routes between this O-D pair. Because only one route is chosen by each traveler agent, ∑j∈Jdjn = 1.
The authors assume that the prior distribution f(pn) follows a Dirichlet distribution with parameter set an = (a1n,a2n,...,ajn). Because the Dirichlet distribution is the conjugate prior of the parameters of the multinomial distribution, the posterior distribution will also be a Dirichlet distribution with parameter set an+1 = an + dn. The probability density function of Dirichlet distribution is defined by:
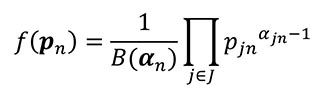 (3)
(3)
In practice, the mean of each random variable E pjn = ajn/a0n is used to represent the subjective probability of the jth route on the nth day, where. For example, suppose on the nth day, the ith route takes the perceived minimum travel time, the posterior subjective probability on the n+1th day can be updated as:
![]() (4)
(4)
![]() (5)
(5)
To provide the parameters for the first day, an initial parameter vector of Dirichlet distribution needs to be given. Then, the Bayesian learning can be repeated iteratively.
This model assumes that all agents use the same Bayesian-updating scheme, but each agent has his or her own perception error on the experienced travel time. Suppose the parameter of Dirichlet distribution has an error term γjn(jth route on nth day), which stands for the perception error. Then the parameter can be expressed as ajn + γjn, where ajnis the deterministic part and γjn is the random part. Assume γjn follows a Gumbel distribution with parameter θ, then the choice probability is given by a multinomial logit model:(171)
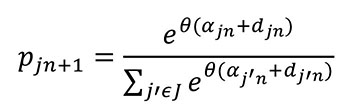 (6)
(6)
Besides his or her own experience, a traveler agent may also, from time to time, acquire the network information (travel time) from other traveler agents or from the environment. The environment here refers to media such as radio and Internet, from which the traveler agent could get travel time information about all routes in the network. In this model, it is assumed that 1 percent of the total agents (called communicating agents) who are randomly selected are given the actual travel time information with respect to all routes in the network. This modification speeds up the convergence rate because the communicating agents tend to make more rational decisions.
Experiment Design
Three experiments were designed and conducted to test and validate the aforementioned proposed model. The first experiment used a simple network to show that the agent-based route choice model is able to reach the same equilibrium solution as obtained from classical traffic assignment models. In the second experiment, the proposed model showed how changes in network topology influence the agents' decisions and how the traveler agents adapt to the new network and form a new traffic pattern. The goal of the third experiment was to test the influence of communicating agents.
A simple network is shown in figure 9. The network has only one O-D pair with three different routes (links). The capacity of each of the three differing routes is 200 vehicles, 400 vehicles, and 300 vehicles, and the free flow travel time of each route is 10 minutes, 20 minutes, and 25 minutes, respectively. The total flow between this O-D pair is 1,000 vehicles. Initial travel times for the first iteration of the experiment were calculated by the Bureau of Public Roads (BPR) function. The network configuration is the same as in the sample network used in Sheffi;(172) thus, the results can be compared with the results obtained by the classical UE models.
The model was implemented in AnyLogic simulation software. In this experiment, the number of traveler agents was 1,000, which is equal to the total O-D flow. Each traveler agent made a route choice every iteration and updated his or her choice probability based on the rules described in the previous section. The initial parameters of the Dirichlet distribution were set to be a1 = (1,1,1). As a result, the choice probability was 1/3 for each route, which suggests that the traveler agents did not have any preference on the routes initially. Each iteration was equal to 30 simulation time units, which means that the travel time and flow were updated every 30 time units.
Experimental Results
Comparison of Agent-Based Model and Classical Route Choice Results
In figure 10, the time plots of flow (A) and travel time (B) on three routes are shown. In figure 10, it is revealed in (A) that the flows on the three routes fluctuated for the first several iterations and then very quickly became stable. It is revealed in (B) that the travel times of the three routes converged to a single value (with travel time of ~25.4 min), which is exactly the same UE point calculated by the Frank-Wolfe Algorithm using the convex combination method found in classical traffic assignment models.
Behavioral Evolution Exhibited in the Agent-Based Route Choice Model
In this experiment, the microscopic simulation was incorporated to obtain travel time instead of BPR function. This microscopic model is characterized by a car-following model and a lane-changing model mainly derived from the Next-Generation Simulation program models. The car-following model is based on Newell's (173) piecewise linear car-following model, with additional considerations such as maximum acceleration, maximum deceleration, travel distance under free flow speed, and safety constraints.(174) The lane-changing model consists of two levels of decision: lane-changing choice model(175) and gap-acceptance model.(174) The lane-changing choice model calculates the probability of whether to change lanes. The changing probability is dependent on the speed differences between the current vehicle and its lead vehicle. The gap-acceptance model calculates the necessary lead and lag gap in the target lane for lane changing. If both gaps are satisfied, the vehicle will perform lane changing. Each vehicle can only change to its immediate adjacent lane in one simulation step.
The same network was used in this experiment as in the first experiment, with one O-D pair and three routes. Different routes had different lengths and different free flow speeds. The total number of traveler agents was reduced to 500, but use of this lower number corresponded to a more realistic travel time, because vehicle interactions affect the travel time. Once the route choice was made, the traveler agents were loaded into the network from a virtual queue at the entrance of each route. Iterations ended when all traveler agents finished their trips. At the end of each iteration, the average travel time of all traveler agents and the flows on each route were recorded. Finally, all traveler agents updated their choice probability and made a route choice before the next iteration.
Experiment II was designed to study travelers' behavioral responses because of a network topology change. A scenario demonstrating the process is illustrated as follows: Routes B and C have three lanes, whereas Route A has two lanes at the beginning of simulation. It is assumed that at the 50th iteration, the government agency decides to expand the capacity of Route A by adding an additional lane. Adding one new lane requires construction work, which lasts a certain amount of time (assumed to be 50 iterations). During the construction period, the capacity of Route A is reduced to half. After completion of the construction, traveler agents can choose among the three lanes with the same probability.
The flow and average travel time on each link is shown in figure 11 and figure 12. The horizontal axis represents the number of iterations. The flows on each route gradually became stable after a certain amount of time, as shown in figure 11. At the 50th iteration, there was an abrupt drop in the flow on Route A, which indicates that the number of available lanes was changed to one, and the travel time of Route A in figure 12 was increased suddenly. Meanwhile, in figure 12 it is revealed that the travel time of Route A between the 50th iteration and 100th iteration varied more severely, because when the capacity was decreased, the travel time was more sensitive to the vehicle interactions captured by car-following and lane changing. After the 100th iteration, construction was complete, and the number of lanes of Route A was increased to three. Therefore, the travel time on Route A was decreased, and the flow of Route A starts to increase gradually. It took about 40 iterations before the flows on each link became stable and the travel time converged to a single value. After about the 140th iteration, a new traffic pattern was formed.
As shown in figure 11, flows dropped fast (only a few iterations) when one lane was closed on Route A: however, it took a longer time for flows to recover to a steady value (~40 iterations) when the blocked lane re-opened and the new lane was made available. Travelers on Route A immediately recognized the sudden delay because of blockage, and because the extra delay was much higher than the risk tolerance (parameter in the model), this triggered the route choice mechanism in the agent-based model with high probability. As a result, flows on Route A dropped quickly because of diversion to alternative Routes B and C. When the capacity of Route A was recovered, traveler agents on Routes B and C had difficulty detecting the recovery of Route A, because they had only partial network information (except for those communicating agents). Those travelers still believed that the travel time on Route A was high, until they happened to randomly experience Route A sometime later; however, the probability of changing routes for traveler agents in Routes B and C at an equilibrium status was rather low. For a different reason, traveler agents already in Route A did not change their routes either, because they were now experiencing a lower travel time. As a consequence, the recovery process was slow. The result is somewhat consistent with similar experiences in a real-world situation, that is, people are more likely to change decisions when experiencing a worse situation but are less likely to change decisions for a better solution-particularly if, because of partial knowledge of the network, the better situation is not obvious. In economics and decision theory, this finding is called loss aversion, which means losses and disadvantages have a greater impact on preferences than do gains and advantages.(176)
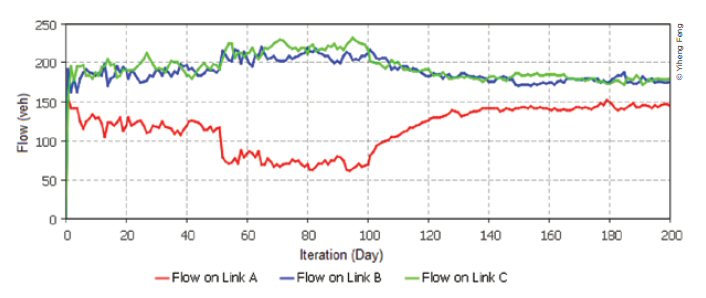
Figure 11. Flows on each route (Experiment II)
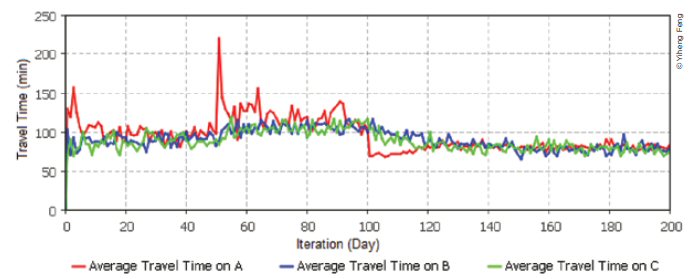
Figure 12. Travel times on each route (Experiment II).
In Experiment III, 10 percent of agents were randomly chosen to be communicating agents (compared with 1 percent in the previous experiment). Communicating agents were aware of 50 percent of the travel times in other parts of the network. That is, if a communicating agent chose Route A, he or she only randomly knew the additional information of Route B or C with 0.5 probabilities, respectively. The same rule was applied to communicating agents who chose Route B or C. The simulation results are shown in figure 13 and figure 14.
Compared with Experiment II, the convergence speed after the construction was much faster in Experiment III. It only took about 13 iterations to converge to a new traffic pattern. Although communicating agents had only partial information about half of the other route travel times, the number of communicating agents was increased 10 fold. Overall, the real-time network information acquired in each iteration for all agents was increased.
Concluding Remarks
For this section, the authors presented an agent-based simulation model exhibiting travelers' route choice behavior. The route choice model considers a traveler's learning from previous experiences, heterogeneity of travelers, partial network information, and communication between travelers and the environment. The proposed model has been implemented in AnyLogic agent-based simulation software. Two experiments were conducted to examine the behavioral characteristics exposed by the model. In the first experiment, the proposed agent-based route choice model reached the same UE solution as reported in classical models in the literature. The second experiment successfully demonstrated how a network topology change influenced the traveler's behaviors and how traveler agents adapted to the new network to form a new traffic pattern.
The authors use this trial example to demonstrate the capability of an agent-based model in studying a transportation system if the agent-based model is armed with a well-defined travelers' behavior component. The example not only successfully replicates the overall performance that the traditional method can accomplish but also provides extra behavioral insights that demonstrate the day-to-day equilibrium process. The behavioral mechanisms of an agent-based route choice model could be flexibly applied in other scenarios to predict the network performance, which is typically not within the classical approach's reach. This agent-based modeling paradigm opens the possibility of studying and understanding the complexity of travelers' decisionmaking under a wide variety of scenarios. The flexibility and extensibility of agent-based modeling allows for the analysis of more complex human behaviors in future work. For example, travel time may not be the only criterion for route choice. Besides, more realistic human decisionmaking models, such as extended BDI, can be employed to mimic travelers' route-selecting process.(25) This paradigm is expected to be deployed to analyze a real-world transportation network with real traffic data.