U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| SUMMARY REPORT |
| This summary report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-15-016 Date: March 2015 |
Publication Number: FHWA-HRT-15-016 Date: March 2015 |
As described in the previous section, behaviors seen in the driving simulator and on the roadway in this research project are generally in agreement, but there are still some mismatches to be addressed. For example, the distribution of speeds observed in the simulator should ideally match speeds observed on the road, but this is not always the case. Simulator characteristics can explain some of the behavior differences, but there are other important characteristics that can lead to differences, including familiarity with the route and individual driver motivations.
Although the mean speed observed on the road compared with the simulator was shown to differ slightly in absolute terms during this study, in relative terms the mean speed was similar.8,20 To solve many design issues, it is important to match simulator and road data in absolute terms. There is a requirement to develop a method to transform simulator data to accurately predict on-road behavior. To meet this requirement, the research team focused on a computational model based on the perceptual, cognitive, and motor-control processes that govern driver speed maintenance. Unlike a regression model, this model uses a theoretical approach to explain the underlying constraints that bound the driver response and provides a way to transform the distribution of speeds observed in the simulator to those observed on the road. This approach offers promise in transforming simulator data to match roadway data and builds on existing models of driver behavior to describe how drivers perceive and respond to road characteristics.
This project also included an analysis of applicable driver models to the roundabout scenarios and integration of these models into a simple speed maintenance model. The research team used data from NADS and the miniSim to estimate the parameters of the model—these simulators were chosen because of their differing configurations. Past research efforts beyond this project to model drivers’ speed choice and improve highway safety and capacity have already produced a series of models that predict drivers’ speed as a function of roadway geometry.21,22 For over 50 years, this has been an ongoing and active research topic, and yet there is still not a definitive model.23,24 Most of these existing statistical models summarize drivers’ speed choice without describing the mechanisms that guide speed selection.25
Process models, however, complement these statistical models and describe the drivers’ perceptual, decisionmaking, and motor control processes.10,26 Process models can describe drivers’ speed selection in terms of an error-correcting mechanism that strives to minimize the deviation from a desired speed. Desired speed might reflect a driver’s ability to steer the vehicle through a curve while maintaining an appropriate distance from the lane boundary, often expressed as the time-to-line crossing.27 Though not part of this research study, one factor that influences this speed choice is traffic in the opposite lane. Without traffic, the research team noted that drivers often cross the centerline to smooth the curve, but most models assume the driver attempts to stay within the lane boundaries. Steering demand increases as the radius of the curvature and lane width decrease and speed increases. Small steering errors at high speed quickly lead a driver toward the lane boundary and forces drivers to slow down to maintain a constant time-to-line crossing. This creates an inverse relationship between lateral acceleration and curve radius and can explain why drivers often choose speeds through curves that are less than what might be expected.12
The research team focused its analysis on four of the six road segments considered in the earlier simulator data collections. These were the two roundabout sections from Arizona and Maryland. Two of these sections are featured in figures 7–10. This group of figures shows a bird’s eye view of the route through the roundabout, with each stage of the route annotated; and below this, the curvature across the segment is shown, also with each stage annotated. The curvature data from these sections were used as the primary input to the driver model, which determines the speed maintenance behavior of the driver model.
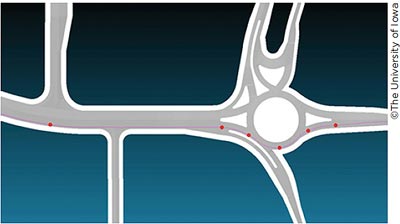 |
| Figure 7. Layout of the first Arizona roundabout. |
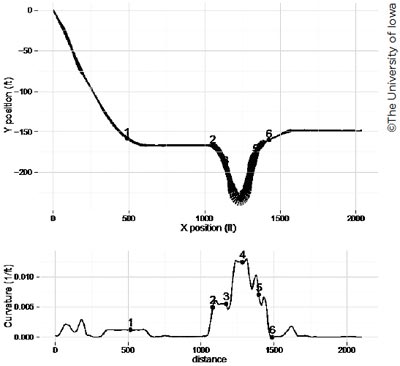 |
| Figure 8. Layout curvature data of the first Arizona roundabout. (The width of the line in the center graph corresponds to the radius of curvature shown in the bottom graph.) |
 |
| Figure 9. Layout of the first Maryland roundabout. |
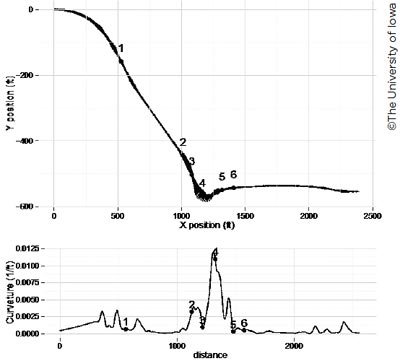 |
| Figure 10. Layout curvature data of the first Maryland roundabout. (The width of the line in the center graph corresponds to the radius of curvature shown in the bottom graph.). |
Model-based transformations aim to directly relate driver behavior observed in the simulator to behavior on the actual roadway. A transformation is made possible by first estimating those model parameters that produce the speed trajectories observed on the road; however, the limited on-road data available for this project make such estimates difficult. The researchers estimated the model parameters for each simulator configuration based on the data collected from the simulators. The resulting parameters reflected how simulator characteristics influence driver behavior. The model can then transform the simulator and estimate roadway data by adjusting the model parameters using a scaling parameter based on the ratio of the roadway parameter to the simulator parameter. This method is subsequently able to describe differences in how drivers negotiate curves through parameters of a dynamic driver model. These parameters can provide a more diagnostic and generalizable description of how driving in the simulator differs from driving on the road. The resulting practical utility of this contribution is that it can be used to transform speed observed in the simulator to speed observed on the road.