Bottomless Culvert Scour Study: Phase I Laboratory Report
2. EXPERIMENTAL APPROACH
TEST FACILITIES AND INSTRUMENTATION
The experiments were conducted in the FHWA Hydraulics Laboratory located at the Turner-Fairbank Highway Research Center (TFHRC) in McLean, VA. Test facilities and instrumentation used during the experiments are described in this section.
Figure 1. View of the flume in the Hydraulics Laboratory.
Hydraulic Flume
The experiments were completed in a 21.34-meter- (m) long by 1.83-m-wide (70-foot- (ft) long by 6-ft-wide) rectangular flume with a 2.4-m-long by 1.83-m-wide (8-ft-long by 6-ft-wide) recessed section to allow for scour hole formation. A 9.14-m (30-ft) flow development section from the head box to the transition section consisted of a plywood floor constructed 0.1 m (4 inches) above the stainless steel flume bottom. The plywood floor was coated with a layer of epoxy paint and sand to approximate the roughness of the sand bed channel in the recessed section. The walls of the flume are made of a smooth glass. The flume was set at a constant slope of 0.04 percent and the depth of flow was controlled with an adjustable tailgate located at the downstream end of the flume. Flow was supplied by a 0.3-cubic meter/second (m3/s) (10-cubic foot/second (ft3/s)) pumping system. The discharge was measured with an electromagnetic flow meter.
Electromagnetic Velocity Meter Operation
A 13-millimeter (mm) spherical electromagnetic velocity sensor (Marsh-McBirney 523) was used to measure equivalent two-directional mean velocities in a plane parallel to the flume bed.
A fluctuating magnetic field was produced in the fluid surrounding the spherical sensor that was orthogonal to the plane of four carbon-tipped electrodes. As a conductive fluid passed around the sensor, an electric potential was produced proportional to the product of the fluid velocity component tangent to the surface of the sphere and normal to the magnetic field and the magnetic field strength. The electrodes located at four locations on the sensor detected the voltage potential created by the flowing water. The voltage potential produced was proportional to the velocity of the fluid flowing in the plane of the electrodes. Two orthogonal velocity components in the plane of the electrodes were measured. Detailed information on the meter operation is available in the technical manual, Instruction Manual Model 511 Electromagnetic Water Current Meter, provided by the probe manufacturer, Marsh-McBirney Inc.
Post-Processing and Data Analysis
Post-processing and data analysis were performed using the LabVIEWTM graphical programming technique for building applications such as testing and measurement, data acquisition, instrument control, data logging, measurement analysis, and report generation. LabVIEW programs are called virtual instruments (VI's) because their appearance and operation imitate physical instruments such as oscilloscopes and multimeters. Every VI uses functions that manipulate input from the user interface or other sources and displays that information or moves it to other files or other computers.
A VI contains the following three components:
- Front panel: Serves as the user interface (figure 2).
- Block diagram: Contains the graphical source code that defines the functionality of the VI (figure 3).
- Icon and connector pane: Identifies the VI so that you can use one VI in another VI. A VI within another VI is called a subVI. A subVI corresponds to a subroutine in text-based programming languages.
Figure 2. Example of a front panel.
Figure 3. Example of a block diagram.
The regression analysis was done using the nonlinear Levenberg-Marquardt fit algorithm to determine the set of coefficients that minimize the chi-square quantity:
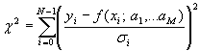 (1)
In this equation, xi and yi are the input data points, and f (xi; a1,...,aM) is the nonlinear function, where a1,...,aM are coefficients. If the measurement errors are independent and normally distributed with a constant standard deviation σi = σ, this is also the least-square estimation.
MODEL BOTTOMLESS CULVERT SHAPES
Three bottomless culvert shapes were constructed and tested: (1) a rectangular model with a width of 0.61 m (2 ft) and a height of 0.46 m (1.5 ft) (figure 4), (2) a CONSPAN model with a width of 0.61 m and a height of 0.45 m (1.46 ft) (figure 6), and (3) a CONTECH model with a width of 0.61 m and a height of 0.42 m (1.36 ft) (figure 8). All three models were evaluated with 45-degree wingwalls (figures 5 and 7) and without wingwalls. The models were constructed of Plexiglas®. Marine plywood was used for the vertical face of the models and for the wingwalls. The models were mounted in the centerline of the flume.
Figure 4. Rectangular model, vertical face.
Figure 5. Rectangular model with wingwalls.
1 inch = 25.4 mm
Figure 6. CONSPAN model.
Figure 7. CONSPAN model with wingwalls.
1 inch = 25.4 mm
Figure 8. CONTECH model.
EXPERIMENTAL PARAMETERS
Steady flow experiments were conducted for approach flow depths of 0.106 m, 0.212 m, and 0.304 m (0.35 ft, 0.7 ft, and 1 ft) and approach velocities ranging from 0.091 to 0.304 m/s (0.3 to 1 ft/s). The discharges to obtain the approach flow conditions varied from approximately 0.019 to 0.14 m3/s (0.7 to 5 ft3/s). The particle size (D50) was varied from 1.2 to 3.0 mm (0.004 to 0.01 ft) for the scour experiments.
Riprap experiments were conducted for uniform particle sizes of 9.5 mm, 12.7 mm, 20.3 mm, and 25 mm (0.375 inch, 0.5 inch, 0.8 inch, and 1 inch). The velocity was increased incrementally until discernible areas of particles were dislodged, which was considered to define the failure condition for that particle size. Because of time constraints, riprap experiments (figure 9) were conducted for the rectangular model with vertical headwalls only. Vertical headwalls were considered a worst-case condition and wingwalls should reduce the riprap size determined from these experiments.
Figure 9. Rectangular model from the scour protection task.
Previous | Table of Contents | Next
| 