U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000

Skip to content
Facebook iconYouTube iconTwitter iconFlickr iconLinkedInInstagram

Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations

Report
This report is an archived publication and may contain dated technical, contact, and link information
Publication Number: FHWA-HRT-07-026
Date: February 2007

Bottomless Culvert Scour Study: Phase II Laboratory Report

Chapter 6: Scour Calculation Examples

This section gives step-by-step instructions for calculating the maximum scour depth for unsubmerged bottomless culverts. Two different scenarios from the results section will be shown.

USING kS AS A FUNCTION OF VRA, VCL, AND F1

The first example is based on using VRA, VCL, and F1. The procedure is as follows:

Step 1: Compute the representative velocity of the flow using the average velocity in the approach section (equation 2) as follows.

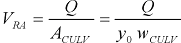28. V subscript R A equals the quotient of uppercase Q divided by A subscript C U L V. This quotient in turn equals the quotient of uppercase Q divided by the product of y subscript 0 times w subscript C U L V. (28)

where:

Q
is volumetric flow through the culvert (m3/s).
y0
is depth of flow in the approach to the culvert before scour (m).
wCULV
is width of the culvert inlet (m).

Step 2: Express the critical velocity computed by Laursen’s method (equation 5) in terms of y2 as follows.

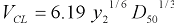29. V subscript C L equals the product of 6.19 times the one-sixth power of y subscript 2 times the one-third power of D subscript 50. (29)

where:

y2
is equilibrium flow depth (m).
D50
is sediment size (m).

Step 3: Everything in the previous two equations should be known except for y2. Now we can substitute the previous two equations into equation 1 as follows.

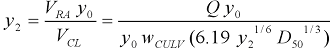30. Lowercase y subscript 2 equals the quotient of the product of V subscript R A times y subscript 0 divided by V subscript C L. This quotient in turn can be expressed as the quotient of two multicomponent terms. The numerator of this quotient is the product of uppercase Q times y subscript 0. The denominator is the product of five terms: y subscript 0, w subscript C U L V, 6.19, the one-sixth power of y subscript 2, and the one-third power of D subscript 50. (30)

This expression can now be rearranged to calculate y2 as follows.

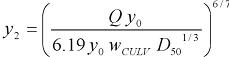31. Lowercase y subscript 2 equals the six-seventh power of the quotient of the product of uppercase Q times y subscript 0 divided by the product of four terms: 6.19, y subscript 0, w subscript C U L V, and the one-third power of D subscript 50. (31)

Step 4: Now use the scour equations from the first entry (ks) in table 2 to calculate the maximum scour, recalling that only the intercept of these equations should be used.

Without wingwalls, the maximum scour is computed with the following equation.

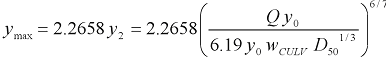32. Lowercase y subscript max equals the product of 2.2658 times y subscript 2. Lowercase y subscript 2 equals the six-seventh power of the quotient of the product of uppercase Q times y subscript 0 divided by the product of four terms: 6.19, y subscript 0, w subscript C U L V, and the one-third power of D subscript 50. (32)

Alternatively, the equation for the maximum scour with wingwalls is as follows.

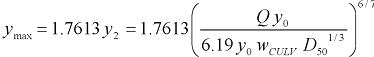33. Lowercase y subscript max equals the product of 1.7613 times y subscript 2. Lowercase y subscript 2 equals the six-seventh power of the quotient of the product of uppercase Q times y subscript 0 divided by the product of four terms: 6.19, y subscript 0, w subscript C U L V, and the one-third power of D subscript 50. (33)

USING ks AS A FUNCTION OF VRM, VCN, AND Qblocked

The second example is based on using VRM, VCN, and Qblocked. The procedure is as follows:

Step 1: Compute representative velocity of the flow using the calibrated velocity in the culvert inlet (equation 22) as follows.

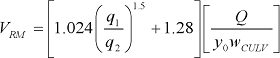34. V subscript R M equals the product of two terms. The first term is the sum of 1.28 plus the product of 1.024 times the quotient to the 1.5 power of q subscript 1 divided by q subscript 2. The second term is the quotient of Q divided by the product of y subscript 0 times w subscript C U L V. (34)

where:

Q
is volumetric flow through the culvert (ft3/s or m3/s).
y0
is depth of flow in the approach to the culvert before scour (ft or m).
wCULV
is width of the culvert inlet (ft or m).
q1
is unit discharge in the approach section (ft2/s or m2/s).
q2
is unit discharge in the contracted section (ft2/s or m2/s).

Note that the unit discharge ratio of q1 divided by q2 can be computed from a width ratio as follows.

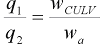35. The quotient of lowercase q subscript 1 divided by lowercase q subscript 2 equals the quotient of w subscript C U L V divided by w subscript lowercase a. (35)

where:

wCULV
is width of the bottomless culvert inlet (m).
wa
is width of the approach section to the culvert (m).

Step 2: Express the critical velocity computed by Neill’s method (equations 6, 7, and 8, or 9) in terms of y2. For example, for D50 sediment size greater than 0.0003 m (0.001 ft) but less than 0.03 m (0.1 ft), the equation for Neill’s critical velocity is given as follows.

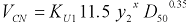36. V subscript C N equals the product of four terms: uppercase K subscript U1, 11.5, the x power of y subscript 2, and the 0.35 power of D subscript 50. (36)

The exponent, x, is calculated using equation 37:

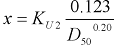37. Lowercase x equals the product of uppercase K subscript U2 times the quotient of 0.123 divided by the 0.20 power of D subscript 50. (37)

where:

y2
is equilibrium flow depth, m or ft.
D50
is sediment size, m or ft.
KU1
is 0.3048(0.65-x) for SI units, or 1.0 for U.S. customary units.
x
is the exponent from equation 8.
KU2
is 0.788 for SI units, or 1.0 for U.S. customary units.

Step 3: Everything in the previous three equations should be known except for y2. Now we can substitute the previous two equations into equation 1 as follows.

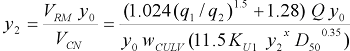38. Lowercase y subscript 2 equals the quotient of the product of V subscript R M times y subscript 0 divided by V subscript C N. This quotient in turn can be expressed as the quotient of two multicomponent terms. The numerator is the product of Q times y subscript 0 times the sum of 1.28 plus the product of 1.024 times the quotient to the 1.5 power of lowercase q subscript 1 divided by lowercase q subscript 2. The denominator is the product of six terms: y subscript 0, w subscript C U L V, 11.5, uppercase K subscript U1, the x power of y subscript 2, and the 0.35 power of D subscript 50. (38)

This expression can now be rearranged to calculate y2 as follows.

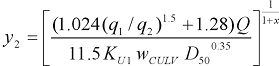39. Lowercase y subscript 2 equals a multicomponent quotient to a power that is a quotient. The quotient that is the power is 1 divided by the sum of 1 plus x. The numerator of the multicomponent quotient is the product of uppercase Q times the sum of 1.28 plus the product of 1.024 times the quotient to the 1.5 power of lowercase q subscript 1 divided by lowercase q subscript 2. The denominator of the multicomponent quotient is the product of four terms: 11.5, uppercase K subscript U1, w subscript C U L V, and the 0.35 power of D subscript 50. (39)

Step 4: Now use the scour equations from the first entry (ks) in table 2 to calculate the maximum scour.

Without wingwalls, the maximum scour is computed with the following equation.

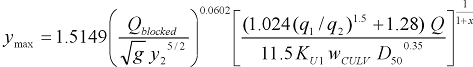40. Lowercase y subscript max equals the product of four terms. The first term is 1.5149. The second term is y subscript 2. The third term is the 0.0602 power of the quotient of uppercase Q subscript blocked divided by the product of the square root of g times the five-seconds power of y subscript 2. The fourth term is a multicomponent quotient to a power that is a quotient. The quotient that is the power is 1 divided by the sum of 1 plus x. The numerator of the multicomponent quotient is the product of uppercase Q times the sum of 1.28 plus the product of 1.024 times the quotient to the 1.5 power of lowercase q subscript 1 divided by lowercase q subscript 2. The denominator of the multicomponent quotient is the product of four terms: 11.5, uppercase K subscript U1, w subscript C U L V, and the 0.35 power of D subscript 50. (40)

Alternatively, the equation for the maximum scour with wingwalls is as follows.

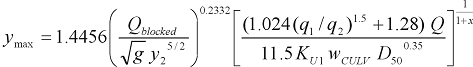41. Lowercase y subscript max equals the product of four terms. The first term is 1.4456. The second term is y subscript 2. The third term is the 0.2332 power of the quotient of uppercase Q subscript blocked divided by the product of the square root of g times the five-seconds power of y subscript 2. The fourth term is a multicomponent quotient to a power that is a quotient. The quotient that is the power is 1 divided by the sum of 1 plus x. The numerator of the multicomponent quotient is the product of uppercase Q times the sum of 1.28 plus the product of 1.024 times the quotient to the 1.5 power of lowercase q subscript 1 divided by lowercase q subscript 2. The denominator of the multicomponent quotient is the product of four terms: 11.5, uppercase K subscript U1, w subscript C U L V, and the 0.35 power of D subscript 50. (41)

Previous | Contents | Next

Return to top

Privacy Policy | Freedom of Information Act (FOIA) | Accessibility | Web Policies & Notices | No Fear Act | Report Waste, Fraud and Abuse
U.S. DOT Home | USA.gov | WhiteHouse.gov

Federal Highway Administration | 1200 New Jersey Avenue, SE | Washington, DC 20590 | 202-366-4000
Turner-Fairbank Highway Research Center | 6300 Georgetown Pike | McLean, VA | 22101