U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-13-038 Date: November 2013 |
Publication Number: FHWA-HRT-13-038 Date: November 2013 |
This appendix presents a summary of major concepts from a literature review of pavement RSL and other industries related to life and product reliability. In the interest of brevity, equations for the various models and statistical mathematical forms have been left out of this review. Those interested in mathematical formulations can reference the citations contained in this report.
The discussion of RSL prediction models requires a categorization scheme that groups models with similar features. The following methods have been used to categorize RSL prediction models:
Prediction model classification schemes can also be based on the type of performance model. Empirical models are primarily founded on statistical approaches, while mechanistic-based models are primarily founded on engineering principles. These categories are not mutually exclusive; however, most of the mechanistic-based models use statistical methods for calibration, and some of the empirical models incorporate engineering principles.
The earliest known survival analysis for pavements in the United States was performed by Winfrey and Farrell.(18) The terminology used in the early years of this work was referenced to the life of the pavement surface. Survival curves were developed for pavements built each year from 1903 to 1937 in 46 States using the life table method. The distribution of survival times is divided into year or half-year intervals. For each interval, the mileage of pavement sections that were still in service in the beginning of the respective interval, the mileage of pavement sections that were out of service at the end of the respective interval, and the mileage of pavement sections that were lost (e.g., a road was abandoned) in the respective interval were counted. The survival probability of each interval was calculated by dividing the remaining mileage by the total mileage in the respective interval. A survival curve was formed by the probability versus time interval graph. RSL was estimated by extrapolating the survival curve to zero percent survival. The past use of the life table method for pavement RSL in the late 1940s, 1950s, and 1960s was documented.(19-21)
These are pure empirical models that apply to the inference space in which they were developed. They are not representative of changes in construction techniques, materials, traffic loads, or definitions of out-of-service pavements.
The Kaplan-Meier survival analysis method, also known as the product limit estimator method, is a statistical technique used to generate tables and plots of survivor or hazard functions for time-to-event data. (22) Advantages of the method are that it accounts for censored data, losses from the sample, and non-uniform time intervals between observations. The method assumes that events are dependent only on time. Since the method cannot differentiate between the life of a thin pavement with high traffic and a thick pavement with low traffic, pavements must be grouped into families that have similar characteristics, traffic loadings, and environments. In essence, a separate survivor curve has to be generated for each factor of interest. The method is incorporated in many popular statistical analysis packages and can provide a useful summary of available data in exploratory stages of research.
The failure time theory has been used to develop survivor curves for pavements. (23,24) The basis of the failure time theory requires that the underlying functional form of the parametric failure distribution be assumed a priori. This allows for the estimation of the coefficients of those parameters, which in effect dictate the influential factors. However, this may not be feasible when the underlying functional form does not match any known parametric statistical distribution.
The Cox PH model has been widely used in clinical trials to analyze the survival probability for patients after a treatment. The median survival time, which is defined as the time when 50 percent of the subjects will fail to maintain a specified physical condition, is often of interest. The distinctive feature of the method is that the ratio of the instantaneous risks of failure (i.e., the hazard ratio) at time t for any two given patients in the study does not change with time. The advantages of this method are that it does not require that the underlying survival distribution be known and the effects of influential factors on survival time can be estimated. A pavement is similar to a clinical trial in that after a period of time, it may fail to provide required serviceability after a treatment. A pavement is considered to have reached the end of its useable life if it is rehabilitated or if its condition falls below a specified criterion.(16)
This method has been used for life prediction in many areas of infrastructure management. Yu developed a Cox PH model for pavements in Ohio using the Ohio pavement condition rating. The rating is based on a 0 to 100 scale where 0 is poor and 100 is excellent. A score of 70 represents a failure condition. Some of the inferences implied by the models developed on this project are counterintuitive. The models are only applicable to the method ODOT uses to rate the condition of their pavements, traffic, and environmental conditions in Ohio as well as other attributes of Ohio pavements.
In the 1986 and 1993 versions of the AASHTO Guide for Design of Pavement Structures, pavement remaining life terminology is used in the overlay design methodology. (11,5) In the 1986 guide, two remaining life estimates are required for the analysis—the remaining life of the pavement prior to overlay and remaining life of the overlaid pavement when it reaches its terminal serviceability condition.(11) These remaining life values are expressed in terms of a percentage and are used to compute a remaining life factor. The remaining life factor is used to discount the effective structural capacity of the pavement prior to overlay in order to determine the structural capacity needs of the overlay. The 1993 guide uses a similar approach where remaining life is expressed as a percentage, but its use is simplified to determine the effective structural capacity of the existing pavement.(5) However, what is called pavement remaining life in these documents is really a way to estimate damage to the existing pavement structure and does not result in an estimate of the time until a terminal serviceability level is reached.
While the 1986 and 1993 versions of the AASHTO Guide for Design of Pavement Structures do not contain a procedure to estimate pavement life in terms of time until the next rehabilitation or reconstruction treatment is required, the design equations used in the methods can be used for this purpose. (11,5) These methods use two basic empirical design equations that relate the number of traffic loadings (expressed in terms of 18-kip (40-kN) equivalent single-axle loads (ESALs)) to pavement structural capacity, subgrade support properties, pavement serviceability changes, and reliability considerations. Estimating the time in years to the specific level of serviceability only requires inputs on the pavement structure layer types and thickness, subgrade properties, 18-kip (40-kN) ESAL applications to date, and the future rate of 18-kip (40-kN) ESAL applications. Using the design equations, the number of total applications the pavement structure can support until reaching the terminal serviceability level of interest is determined. Subtracting the total ESAL applied to the pavement from the total the pavement will support provides the remaining ESAL loadings until the terminal serviceability is reached. Dividing this by the ESAL rate per year provides a time estimate. The time to rehabilitation or reconstruction can be simulated by changing the terminal serviceability level. This is the approach that was previously used by the HPMS models as described in the next section of this appendix.
One of the more severe issues with using the older AASHTO pavement models for pavement remaining life analysis is that they are pavement design equations, which are not necessarily created as performance prediction models. Further, the models incorporated in the 1986 and 1993 AASHTO guides can be traced back to the AASHO Road Test.(11,5,4) The Road Test data inference space is severely limited.
The remaining life models used for the HPMS analytical process and HERS model are changing. The initial models were based on the 1972 AAHSTO Interim Guide for Design of Pavement Structures equations. (8) This required pavement condition is expressed in terms of PSR and pavement structure capacity as SN for flexible pavements and slab thickness for PCC pavements. Using this system, resurfacing or reconstruction was indicated by the level of PSR. When the pavement PSR in an analysis cycle dropped below a minimum tolerable condition based on highway functional classification, resurfacing was indicated. Reconstruction was triggered if the PSR dropped below the reconstruction threshold. The default minimum tolerable condition and reconstruction PSR values are shown in table 2.(25) For some rural facilities, the average daily traffic (ADT) was also used to discriminate the minimum tolerable condition, with lower volume facilities having lower trigger points. In the late 1980s data submittal requirements for pavement roughness measurements reported as IRI was added.
Table 2. PSR threshold values used in the HPMS analytical process for minimum tolerable conditions for overlay and reconstruction.
Location |
Facility Type |
Minimum Tolerable Condition (PSR) |
Reconstruction PSR |
|---|---|---|---|
Rural |
Interstate |
3.0 |
2.0 |
Other principal arterial |
3.0/2.8 (6,000 ADT) |
2.0 |
|
Minor arterial |
2.4 |
1.5 |
|
Major collector |
2.0 |
1.1 |
|
Minor collector |
1.8 |
0.8 |
|
Urban |
Interstate |
3.2 |
2.2 |
Other freeway and expressway |
3.0 |
2.0 |
|
Other principal arterial |
2.8 |
1.8 |
|
Minor arterial |
2.4 |
1.1 |
|
Collector |
2.0 |
1.0 |
One of the outcomes of the reassessment of the HPMS in 2006 was the development of a new data model based on inputs related to the models used in the MEPDG. (7) Pavement-related data requirements were expanded and include the following: (26)
The development of simplified models for HERS and NAPCOM was reported by FHWA in 2007.(27) The objective of this work was to develop simplified models based on the MEPDG that could be used with HERS using HPMS data. The definition of RSL for this project is the time in age or traffic applications from initial construction or reconstruction to the first major rehabilitation. The following pavement distress prediction models were reported to be under development:
A key concept in applying these models was to adjust the predictions from the MEPDG design models to current observations contained in the HPMS dataset. It appears that the magnitudes of the predicted distress level from the model were adjusted to the field observations, and future predictions were based on the rate of increase according to pavement age.
Recently, FHWA has developed a PHT analysis tool for HERS and NAPCOM purposes that uses HPMS data. (28) Models based on use of the default level 3 MEPDG inputs along with the HPMS data are used to predict changes in the multiple pavement condition measures adjusted for current observed levels. In this application, pavement health is defined as the time in age or load applications from initial construction or reconstruction to the first major rehabilitation as warranted by pavement ride and structural conditions. The following distress prediction models are included in the tool:
The following examples highlight contemporary RSL models developed within the pavement engineering community:
George developed a graphical procedure to determine RSL based on the effective thickness ratio derived from nondestructive deflection testing.(29)
Mamlouk et al. computed RSL based on a fatigue model (considering the rate of crack development in Arizona) in conjunction with the backcalculated moduli.(30)
Huang used two general mathematical distress models to determine the remaining life of flexible pavements.(31)
Park and Kim and Werkmeister and Alabaster developed RSL models based on FWD measurements.(32,33)
Santha et al. developed a simple, mechanistic rut-depth prediction model that, when used with estimated current traffic, yields the RSL.(34)
Ferregut et al. and Abdallah et al. applied artificial neural network techniques to develop algorithms that combine the functional condition of a pavement (i.e., percent cracking and depth of rut) at the time of FWD testing with simple remaining life algorithms to predict the remaining life of pavements.(35,36)
Zaghloul and Elfino used backcalculated layer moduli and expected traffic volumes to estimate the RSL of homogeneous sections.(37)
Many of the approaches discussed have great potential to be used at the project level. Due to the mechanistic approach of most of these contemporary models, they also have potential to be used for public-private partnership-type projects as the results are scientifically based and are likely defensible from both the agency and concessionaire perspectives. Used with a cost estimating model, these methods could be used to determine the remaining value of a given project.
Many mechanistic approaches rely on determining the structural response of a pavement from the various devices that measure the deflection of a pavement surface under various types of applied loads. The Long-Term Pavement Performance (LTPP) program has shown that deflection measurements possess seasonal variability in the measured responses that can introduce uncertainty if corrections are not made for these effects. By definition, preservation treatments do not add structural strength to the pavement section. As a result, deflection measurements do not account for the increase in service life provided by preventative treatments.
NCHRP Project 08-71, Methodology for Estimating Life Expectancies of Highway Assets, began in July 2009.(39) The objectives of this research were to develop a methodology for determining the life expectancies of major types of highway system assets for use in LCCA supporting management decisionmaking; demonstrate the methodology's use for at least three asset classes, including pavement or bridges and two others, such as culverts, signs, or signals; and develop a guidebook and resources for use by State transportation departments and others for applying the methodology to develop highway maintenance and preservation programs and assess the impact of such programs on system performance.
Pavement was one of the assets studied under this project. The following information concerning pavement life expectancy was obtained from NCHRP Report 713: Estimating Life Expectancies of Highway Assets, Volume II: Final Report.(40) Traffic loading in particular has been studied with field tests for trucks with various suspensions for both static and dynamic loads. Traffic loading is considered a better indicator of service life than age, although there is a correlation between the two factors; reliability curves built on traffic loading are often used to predict service life. Other than traffic loading, the amount of distress is primarily utilized. To determine the most influential distress type, studies have used a discriminate analysis approach. Depending on the pavement type (e.g., asphaltic, concrete, gravel, etc.), additional factors affect the life expectancy.
For pavements, factors that affect life expectancy include surface type (i.e., rigid, flexible, and composite), design and construction features, traffic loading, climate, age, frequency, and intensity of pavement M&R. For each surface type, the project will consider the different pavement subtypes and thicknesses. The influence of traffic loading will be investigated on the basis of the load spectra. Also, literature will be reviewed on the influence of vehicle dynamics to gain information on the expectations from the analyses of life expectancy sensitivity to operations. The impact of climatic severity on pavement life expectancy will be expressed in terms of variables such as freeze index, average temperature, and the number of freeze-thaw transitions. The incorporation of M&R activities will be done by determining the impact of specific M&R treatments on life extension and determining the impact of different M&R annual expenditures (cost per lane-mile) on life extension. The final selection and analysis of influential factor sensitivities will be guided by the availability of data. Methods for assessing the sensitivities will include the Cox PH model.
The forecasting of friction is typically performed as a function of environmental variables in an effort to predict skid resistance throughout changing weather conditions and seasons. There are many models that currently accomplish this goal, but they do not forecast long-term conditions. In order to incorporate surface friction characteristics into a pavement life discussion, the focus must be on the long-term trend in friction.
Several models have been proposed to predict future skid resistance-based on factors such as material properties, traffic loading, and age. Using data from Toronto highways, Emery developed an equation in 1982 based on Marshall stability, Marshall flow, mix air voids, and a commercial vehicle equivalency factor.(41)
The Wisconsin Department of Transportation developed models in 1996 that predict friction number (FN) at 40 mi/h (64 km/h) based on aggregate properties and traffic characteristics for HMA and PCC surfaced pavements.(42) Independent variables include percent dolomite in the coarse aggregate, Los Angeles wear rate, accumulated vehicles passes, and percent heavy vehicles.
A 2006 study using Maryland SHA skid data suggests a much simpler prediction model based on the age of the pavement.(43) The authors show that FN at 40 mi/h (64 km/h) decreases approximately 0.22 FN per year on rural roads and 0.26 FN per year on urban roads. These rates are valid only after an initial period of high friction loss (approximately the first year).
The development of pavement age/traffic application friction models were reported by Ahammed and Tighe in 2009.(44) Two models each for AC and PCC surfaced pavements were developed based on either pavement age or cumulative traffic passes. These models are based on LTPP data, which has a much broader geographic scope than many of the other models, whichare typically based on local/regional datasets. These models use a speed term to predict skid number at different speeds instead of modeling skid number at just one speed. A unique observation modeled in this work is that pavement friction will essentially reach a steady state and not continue to degrade with more traffic or age. Although not incorporated into the models, the authors also suggest that friction will start to increase as the pavement reaches old age due to degradation of the pavement surface through mechanisms such as raveling on AC pavements.
Synthesis reports in 2000 and 2005 document agency practice with respect to acceptable friction values.(45,46) Agencies tend to have FN threshold limits between 20 and 30, but those limits are typically accompanied by other factors such as crash history or a known friction problem.
The friction threshold in current practice is for maintenance activity, not rehabilitation or reconstruction. Treatments such as diamond grinding, open-graded friction course, chip seal, or simply posting signage to indicate a low friction area are often used. However, there is no indication that any agency currently uses surface friction characteristics as a part of pavement life determination.
The goal of noise prediction is to predict noise at some location away from the roadway given a particular noise level at that roadway. None of the major models attempt to predict noise at some future point in time, as it is not considered a necessary factor in determining pavement life.
Similar to friction, there is no indication that agencies use noise as a factor in determining pavement life, and the actions taken in cases of excess noise are not rehabilitative in nature. Surface treatments such as grinding, grooving, and thin overlays of various types are used to improve noise characteristics along with external remedies such as sound barriers and other roadside design features. (47,48)
The body of literature from outside the field of pavements provides a rich source of information on theoretical models and terminology that are relevant to pavements. The following list provides some key concepts captured by the study team from a review of available information outside the field of pavements:
A repairable system can be restored to satisfactory operation by any action, including parts replacements or changes to adjustable settings. Failure rates and hazard rates only refer to the first failure times for a population of non-repairable components.(49)
In a non-repairable population, individual items that fail are removed permanently from the population. While the system may be repaired by replacing failed units from either a similar or a different population, the members of the original population dwindle over time until all have eventually failed.
Lifetime distribution models are theoretical population models used to describe unit lifetimes. The population is generally considered to be all possible unit lifetimes for all units that could be manufactured based on a particular design, choice of materials, and manufacturing process.
Alternate types of probability density functions (PDFs) are used to describe lifetime distribution models.
A cumulative distribution function is the probability that a unit will fail between times defined by the PDF. It is the integral, or area under the PDF curve, between time events in the PDF.
The reliability function or survivability function are defined by the probability that a unit survives beyond a specified time. The general rule is to calculate the reliability of a system of independent components and multiply the reliability functions of all the components together.
Failure rate is defined for non-repairable populations as the (instantaneous) rate of failure for the survivors to time during the next instant of time. The failure rate is sometimes called a conditional failure rate since the population of survivors used in the denominator converts the expression into a conditional rate, given survival past time.
The concept of virtual age accounts for the effect of the repair strategy on future system performance modeling. If a repair returns a system back to an initial state of performance, the virtual age of the system is reset to zero. At the other extreme are minimal repairs that have no impact on future performance of the system and the virtual age is equal to the actual age of the system.(50)
For many years and across a wide variety of mechanical and electronic components and systems, empirical population failure rates have been calculated as units of age over time and repeatedly obtained the "bathtub curve", which illustrates instantaneous failures rates over a product's life. The bathtub curve concept is depicted in figure 11 and has three distinctive time periods: the early life or infant mortality period, constant failure rate or useful life period, and end-of-life or wear out period. The high rates of failure during the early life or infant mortality period are characteristics of weak units with manufacturing or other defects. The early period is followed by a period of relatively constant failure rate also known as the intrinsic failure, normal, or useful life period. During this period, failures tend to be more random in nature due to various effects that impact life depending on the type of component. This is followed by the wear out period when the failure rate increases at the end of the product life.
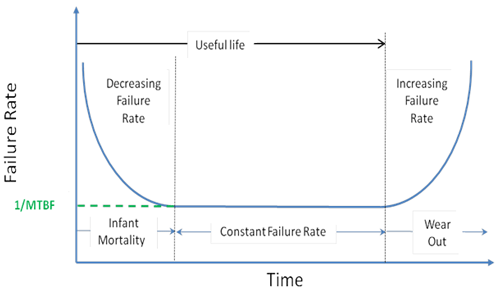
Figure 11. Graph. Classical bathtub curve of component failure rate versus time.
The bathtub curve is expressed as a function of failure rate. Failure rate is expressed in units of failure per component-time. Standards for the mean time between failures (MTBF) statistic are defined as the reciprocal of the failure rate during the constant rate failure period when the failure rate is a minimum value. (51) In many interpretations, the component part of the statistics is not stated and the units are expressed as time/failure, which can be deceiving since it has no direct relationship to the life of a product. For example, it is possible for a product to have a MTBF exceeding 100 years since it is based on the minimum failure rate but have a life expectancy of less than 10 years based on the time until the electrical component or system actually fails. Although MTBF is useful for relative comparison of different components or devices, it is not an indicator of expected life.
A comprehensive and continuously updated source of information the project team found comes from the National Institute of Standards and Technology and Semiconductor Manufacturing Technology NIST/SEMATECH e-Handbook of Statistical Methods.(49) The following list contains information on the various concepts and models from this handbook:
Repair rate models are based on counting the cumulative number of failures over time. Time is measured by system power-on hours from initial turn-on at time zero to the end of system life. Failures occur at given system ages, and the system is repaired to a state that may be the same as new, better, or worse.
The repair rate or rate of occurrence of failures is the mean rate of failures per unit time or the first derivative of average or expected number of failures for each time segment.
Acceleration models predict time to failure as a function of stress. Acceleration factors show how time-to-fail at a particular operating stress level (for one failure mode or mechanism) can be used to predict the equivalent time to fail at a different operating stress level. Acceleration models are usually based on the physics or chemistry underlying a particular failure mechanism. Successful empirical models often turn out to be approximations of complicated physics or kinetics models when the theory of the failure mechanism is better understood. Some acceleration models are as follows:
The following parametric models have successfully served as population models for failure times arising from a wide range of products and failure mechanisms. Some models are probabilistic arguments based on the physics of the failure mode that tend to justify the choice of model. Other models are used solely because of their empirical success in fitting actual failure data.
The exponential model, with only one unknown parameter, is the simplest of all life distribution models. The exponential model is used for the flat portion of the bathtub curve, where most systems spend most of their lives. Mathematical equations can be found in section 8.1.6.1 of the NIST/SEMATECH e-Handbook of Statistical Methods.(49)
The Weibull model is a very flexible life distribution model with two basic parameters that can be increased to three by introducing a waiting time parameter. Because of its flexible shape and ability to model a wide range of failure rates, the Weibull model has been used successfully in many applications as a purely empirical model. The Weibull model can be derived theoretically as a form of extreme value distribution, governing the time to occurrence of the weakest link of many competing failure processes. Mathematical equations can be found in section 8.1.6.2 of the NIST/SEMATECH e-Handbook of Statistical Methods.(49)
Extreme value distributions are the limiting distributions for the minimum or the maximum of a very large collection of random observations from the same arbitrary distribution. In the context of reliability modeling, extreme value distributions for the minimum are frequently encountered. The extreme value distribution is useful for modeling applications for which the variable of interest is the minimum of many random factors, all of which can take positive or negative values. Mathematical equations can be found in section 8.1.6.3 of the NIST/SEMATECH e-Handbook of Statistical Methods.(49)
The lognormal life distribution, like the Weibull model, is a very flexible model that can empirically fit many types of failure data. The lognormal model can be theoretically derived under assumptions matching many failure degradation processes common to electronic (semiconductor) failure mechanisms. Some of these are corrosion, diffusion, migration, crack growth, electromigration, and, in general, failures resulting from chemical reactions or processes. Mathematical equations can be found in section 8.1.6.4 of the NIST/SEMATECH e-Handbook of Statistical Methods(49)
The gamma distribution is a flexible life distribution model that may offer a good fit to some sets of failure data. The gamma is used in standby system models and also for Bayesian reliability analysis. The chi-square distribution is a special case of the gamma distribution. Mathematical equations can be found in section 8.1.6.5 of the NIST/SEMATECH e-Handbook of Statistical Methods (49).
The 1969 Birnbaum and Saunders fatigue life distribution model is based on a physical fatigue process where crack growth causes failure. The Birnbaum-Saunders assumption, while physically restrictive, is consistent with a deterministic model from materials physics known as Miner's Rule or Miner's Hypothesis. Mathematical equations can be found in section 8.1.6.6 of the NIST/SEMATECH e-Handbook of Statistical Methods (49).
The Cox PH model has been used primarily in medical testing analyses to model the effect of secondary variables on survival. It is more like an acceleration model than a specific life distribution model, and its strength lies in its ability to model and test many inferences about survival without making any specific assumptions about the form of the life distribution model. This type of model was developed to predict the remaining life of pavements in Ohio using a PCI type of rating system.(16)
As documented in the literature review performed for this project, many of these concepts and statistical distributions have been used in the pavement industry to predict pavement performance and time until intervention is required.
The terminology and statistics related to repairable systems offer a good theoretical basis for future development of pavement RSL models. A pavement is a repairable system. The concept of virtual age of a system appears to have some applicability to pavements. Some examples of the application of the virtual age concept to improvement of pavement models include the following:
Pothole patching is a minimal repair that does not change the rate of damage accumulation along the structure. The virtual age of the pavement system is still equal to the actual age after patching of spot surface defects.
Replacement of the upper surface layer of an AC/HMA pavement designed for top-down cracking before the cracks extend too deep into the bound portions of the pavement structure is an example of a repair that can return a system to a new condition and reset the virtual age of the system to zero in terms of distress prediction models.
Mill and overlay repair techniques fall somewhere between the minimal and perfect repair scenarios. While these repairs do not return the pavement system to a "good as new condition," they should reduce the virtual life starting point in a RSL model by some fraction. In other words, while the repair/treatment does not return the pavement to good as new status, it should retard the distress rate to an earlier virtual model age.
Most pavement reconstruction activities can be considered as repairs since they tend to only affect the upper bound portions of a pavement structure. The parts of the pavement system related to embankments, base layers, subsurface, and surface drainage features tend to not be changed unless they are identified as a significant contributor to the cause of pavement degradation.
The following observations are based on the literature review of pavement RSL models and concepts from outside the pavement industry related to the objectives of this project:
General empirical population models based on concepts such as survivor curves are applicable only to the population on which they are based. The basis for these statistics tends to be ill-defined and do not account for changes in pavement technology. One must wait more than 10 years for this type of statistical inference base to catch up with technology changes.
Current pavement service life prediction models are by necessity specific to the condition measurement system on which they are based.
Pavement condition prediction models are specific to the condition and inference space for which they were created. This means that a model based on a measurement standard used in one jurisdiction is only applicable to agencies that use the same measurement standard and have similar types of pavement structures, with similar age, materials, and traffic/environmental conditions.
In this review, pavement surface friction is treated as a defect repairable by maintenance types of treatments. Pavement noise prediction models are rarely associated with a pavement life history model that associates increased noise as a function of pavement structure age. While pavement surface texture can affect noise generation, pavement noise is not a first order consideration in the application of pavement treatments.
Modeling terminology and concepts based on repairable systems from literature appear to be a good basis for future developments in pavement condition modeling. The virtual system age concept related to the impacts of maintenance, repair, and restoration treatments offers a good nomenclature framework to describe the effects of pavement corrective treatments.
Advanced statistical modeling techniques exist for system reliability based on a defined numerical measurement system and nomenclature related to repairable systems.
A common issue in all service life models both within and outside the pavement industry is the basis for failure threshold limits. The SI developed at the AASHO Road Test used a human panel to rate pavement acceptability.(4) Subjective ratings are known to change with time, technology, location, visible maintenance features, in-vehicle noise, and other conditions. Combined distress indices often use threshold limits whose basis is not well documented or hard to find. One study of acceptable road roughness found that 15 percent of users found roughness levels higher than 170 inches/mi (2.7 m/km) to be acceptable, although this is still a suggested threshold value for roughness.(52)