Pavement Structural Evaluation At The Network Level

PDF Version (987 KB)

This document is a technical summary of the Federal Highway Administration (FHWA) report, Pavement Structural Evaluation at the Network Level (FHWA-HRT-15-074).⁽¹⁾ It addresses the use of traffic speed deflection devices for the structural evaluation of pavements at the network level. Highlights from three major efforts—gathering information to identify viable devices, performing field trials at or near the Minnesota Department of Transportation MnROAD pavement test track facility near Maplewood, MN, to evaluate viable devices, and analyzing data to identify and select the best deflection indices—are presented. Suggestions for implementation of the results within network-level pavement management system (PMS) applications are also provided as well as recommended technology improvements.

INTRODUCTION

State highway agencies (SHAs) invest billions of dollars each year on providing and managing the transportation infrastructure, and pavements represent a major component of those assets. Prudent and farsighted pavement investment decisionmaking is one of the most critical, costly, and complex elements. At the heart of the decisionmaking process is the PMS, which provides condition indices or scores for each pavement segment in the network. Current PMSs are driven by distress (i.e., cracking, rutting, faulting, etc.) and ride quality, typically in the form of the International Roughness Index (IRI) as key pavement performance indicators. While both merit emphasis within the PMS process, another important indicator to making rational pavement investment decisions is structural adequacy, which is most often determined based on deflection testing.

There is presently a large array of deflection testing equipment, but the most commonly used device in the United States since the 1980s is the falling weight deflectometer (FWD). While FWDs provide many benefits, they are not without shortcomings. Because they are a stop-and-go operation, lane closures are required, which cause traffic disruptions. Additionally, production rates are lower than those associated with a continuous testing operation. These shortcomings are especially important in terms of network-level PMS applications, which typically require information on large pavement networks measuring in the thousands of miles.

To overcome these shortcomings, organizations in the United States and Europe have developed devices that can measure pavement deflections at posted traffic speeds. Recognizing the potential benefits of these devices, FHWA commissioned a research study to assess and evaluate the capabilities of existing devices and develop methodologies for enabling their use for pavement structural evaluation at the network level. The ultimate goal was to establish a reliable measure of pavement structural condition based on traffic speed deflection technology. This TechBrief presents the major findings, conclusions, and recommendations with a focus on network-level PMS applications.

VIABLE DEVICES AND FIELD TRIALS

Much of the initial effort focused on gathering information related to potentially viable devices. A literature review was performed to investigate and evaluate previous and ongoing research projects related to available traffic speed deflection devices (TSDDs) that had the potential to meet the project objectives. It was concluded based on the literature reviewed that both the Applied Research Associates, Inc. (ARA) Rolling Wheel Deflectometer (RWD) and the Greenwood Engineering Traffic Speed Deflectometer (TSD) were potentially viable TSDDs that merited further evaluation.⁽¹⁾ Photographs of the two devices are shown in figure 1 and figure 2, respectively.

Figure 1. Photo. ARA RWD.

Figure 2. Photo. Greenwood TSD.

To augment the literature review findings, questionnaires were developed and sent to the device manufacturers as well as owners and users of the devices. Table 1 provides a summary of the two devices based on information provided by the manufacturers. Updates were made to both devices subsequent to the questionnaires (e.g., number of measurement locations for the RWD and TSD devices evaluated in this study were two and six, respectively). Interviews were also conducted to follow up with specific questions or to pursue clarification. These activities further reinforced the RWD and TSD as TSDDs potentially capable of meeting the project objectives.

1 inch = 25.4 mm
1 mi/h = 1.61 km/h
mil = 0.0254 mm
1 kip = 4.45 kN

In light of the findings from the literature review and user and owner questionnaires and interviews, a work plan was developed to conduct field trials to confirm that the two TSDDs selected met a minimum set of specifications related to the structural evaluation of pavements at the network level. The most critical specifications were accuracy and precision of the measurements, but other specifications also included monitoring of the applied load, operating speed, distance between measurements, and reporting of measured deflections.

The MnROAD facility was selected as the primary site for the field trials since it provided a multitude of test sections in one location as well as a wealth of readily available information, including pavement structure, pavement condition, and environmental and dynamic load response data. In addition, an 18-mi (29-km) roadway network loop in Wright County, MN, was tested. This loop provided not only realistic test sections, but it also contained tight turns and rolling hills that provided data to evaluate the effects of horizontal and vertical curves.

In addition to the existing MnROAD sensors (i.e., linear variable differential transformers, strain gauges, pressure cells, moisture gauges, thermocouples, and tipping buckets), 4 geophones and 1 accelerometer were installed to measure deflection velocity and displacement parameters at 4 cells for a total of 20 sensors. The pavement cross sections for these cells are shown in figure 3, which include three flexible cells covering a range of stiffnesses and one rigid pavement cell. The sensors were embedded in the right wheel path at each cell—two of the geophones and the accelerometer were installed along the center of the wheelpath, while the other two geophones had a 6-inch (152.4-mm) offset to either side of the wheel path center. The performance of each sensor was then verified using an FWD. One of the FWD sensors was placed directly on top of one of the embedded sensors, and the deflections reported by the FWD were then compared with the corresponding deflections reported by the embedded geophones and accelerometers. The results from this activity from all 20 installed sensors are presented in figure 4. The deflections from the two systems were similar.

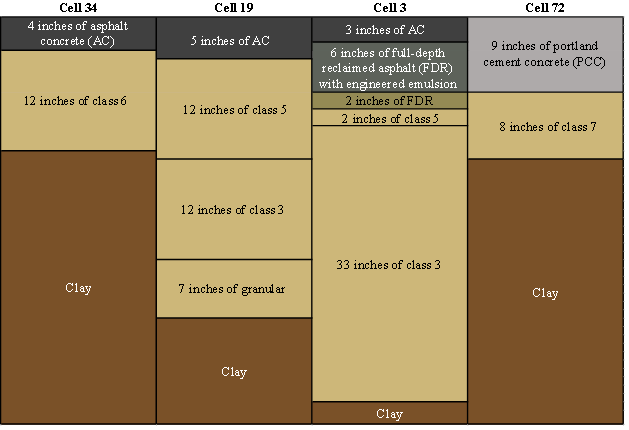
1 inch = 25.4 mm

Figure 3. Illustration. Pavement structure cross section of accuracy cells.

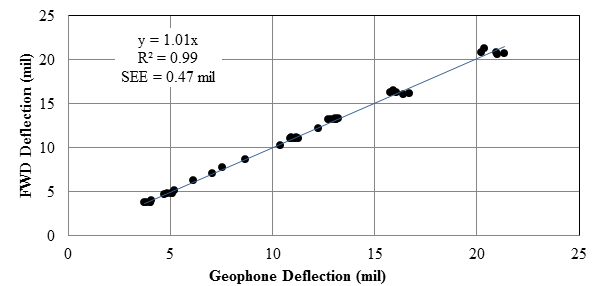
R² = Coefficient of determination.
SEE = Standard error of estimate.
1 mil = 0.0254 mm

Figure 4. Graph. Evaluation of performance of embedded sensors with FWD.

The installation of the sensors took place the week of September 16, 2013, and the actual field trials took place during the week of September 23, 2013. Data from the sensors were used to establish the accuracy of the TSDDs. Specifically, accuracy was established by statistically comparing the results measured with the newly installed sensors with those reported by the TSDDs on three separate repeat passes. The deflection measurements from the rigid cell were not used because the slab did not show a localized deflection basin, and the magnitudes of the signals reported with the TSDDs and newly installed sensors were too small to be accurate given their stated sensitivity. Figure 5 and figure 6 show the overall accuracy results for the three flexible cells for the TSD and RWD, respectively. The constant, the slope of the best-fit line through the data, average deviation, R², and SEE were used to assess accuracy.

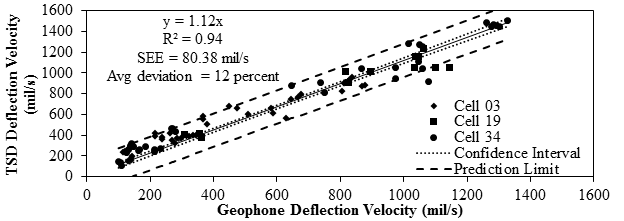
1 mil = 0.0254 mm

Figure 5. Graph. Comparison of geophone and TSD measurements.

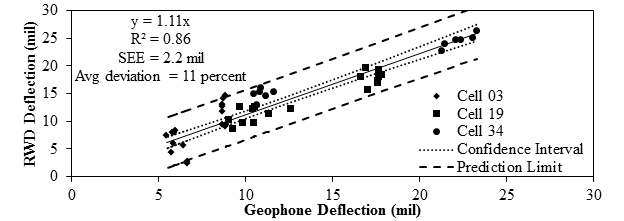
1 mil = 0 .0254 mm

Figure 6. Graph. Comparison of geophone and RWD measurements.

The precision analysis included almost all cells at the MnROAD facility plus the 18-mi (29-km) loop in Wright County, MN. At the MnROAD facility, the TSDDs made up to five passes at two to three different speeds two times a day (early morning and late afternoon). The results from different passes for each device were plotted and visually inspected to confirm the proper alignment of the data (see figure 7). Statistical analyses were then carried out between each two individual pairs of data collected in different passes. Figure 8 illustrates the comparison of data from the first and second passes of the TSDDs. Statistical parameters such as the R² value, slope of best-fit line, and SEE were estimated for each pair. In addition, the minimum, maximum, and median values of each of these statistical parameters were extracted, and histogram plots were developed to visually evaluate the distributions of the data.

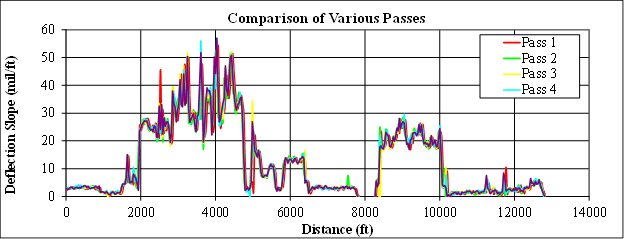
1 mil/ft = 0.083 mm/m
1 ft = 0.305 m

Figure 7. Graph. Precision comparison of passes.

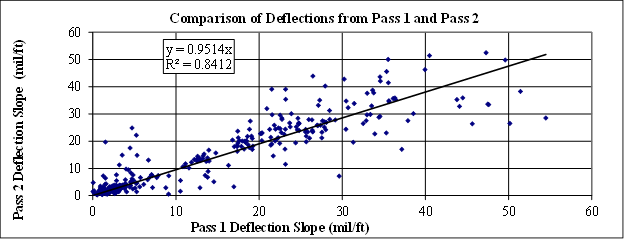
1 mil/ft = 0.083 mm/m

Figure 8. Graph. Precision linear comparison of passes.

While the performance of the RWD and TSD varied under different conditions, it was found that both devices were capable of providing reasonably accurate and precise pavement response measurements. Moreover, the findings from the accuracy and precision analyses were used to recommend optimum operational conditions and device limitations.

DEFLECTION INDEX-PAVEMENT RESPONSE RELATIONS

Having established that the TSDDs in question were acceptable, the 3D-Move software, which estimates dynamic responses at any given point within the pavement structure using a continuum-based finite layer approach, was calibrated for use in the development of a methodology for incorporating TSDD measurements into network-level PMS applications.⁽²⁾ A key element in the calibration was simulating pavement deflections using numerical models with a focus on understanding the parameters that affect the TSDD measurements, including vehicle speed, loadings, and pavement layer properties.

Numerous calibration runs were performed, and the results ultimately bracketed the measured deflection time histories (peak and basin) from the project geophones. As shown in figure 9, there was a good comparison (R² = 0.94) between computed (by 3D-Move) and measured (by sensors) maximum deflections. In addition, it was also important to capture the characteristic of the deflection basins (shapes and pulse width) since the TSDDs use measured deflections at various radial distances to estimate pavement structural conditions. As was the case with the maximum deflections, the calibrated 3D-Move software was able to bracket the deflection basins.

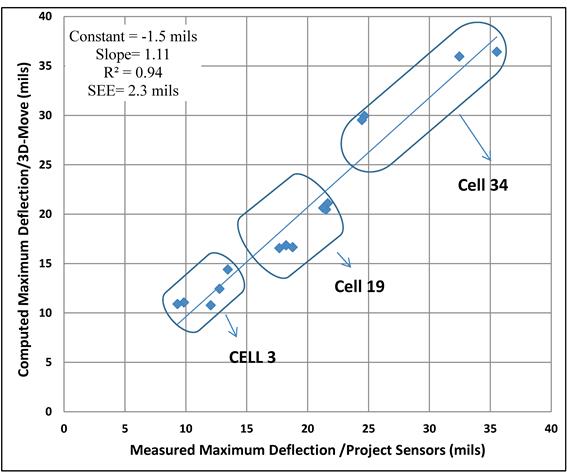
1 mil = 0.0254 mm

Figure 9. Graph. 3D-Move computed versus measured maximum deflections.

The 3D-Move software was further calibrated using strain measurements taken by MnROAD strain gauges at various interior pavement locations. Since load-induced strains are critical inputs to performance predictions, this effort was essential in the applicability of the 3D-Move software for pavement response predictions to be used in identifying the most promising indices from TSDD measurements that best relate to pavement structure. Again, numerous 3D-Move runs were performed, and the results were compared to the MnROAD sensor measurements, which showed that the maximum strains correlated well between the two data sources.

Using the calibrated 3D-Move software, an analytical investigation was then performed to explore relationships between load-induced pavement structural-related response and the corresponding surface deflection basin-related indices. Pavement structural capacity could be estimated from performance prediction equations, which relate load-induced pavement responses to one or both of the following two pavement distresses: AC fatigue cracking and subgrade rutting. The critical load-induced pavement responses that relate to these two distresses were the maximum tensile strain at the bottom of the AC layer and the vertical compressive strain on top of the subgrade, respectively. In light of the project goal and objectives, the focus of this project was on fatigue cracking and, therefore, AC tensile strains.

Numerous deflection basin-related indices have been proposed by researchers that are perceived as strong predictors of the critical structural-related responses and conditions (or capacity) of the pavements.⁽¹⁾ Many of these, as well as others proposed by the project team, were investigated for a total of 75 indices. Each index was evaluated as follows:

1. The deflection indices that showed good correlation with the critical pavement responses were identified using the 3D-Move calibration results (42 datasets), which were based on the TSDD field trials carried out at the MnROAD facility.
   
   
2. A sensitivity analysis of the correlations associated with various deflection indices (not limited to those from step 1) was performed using a set of 36 pavement structures with different layer thicknesses and moduli at several vehicle speeds as input to 3D-Move.
   
   
3. The robustness of the correlations identified in the first two steps was further explored by considering a much larger database of approximately 15,000 pavement structures generated using the layered elastic program, Jacob Uzan Layered Elastic Analysis (JULEA).⁽³⁾

After evaluating the indices based on the first two datasets, the most promising indices were identified and are summarized in table 2, which includes the name of each index as well as its symbol and R² value. The subscript in the symbol identifies the radial distance in inches (from the load center) at which the corresponding deflection values are used to compute the index. When two subscripts are included and separated by a minus sign, it indicates that the index is the difference in deflection values at the radial distances denoted by the subscripts. For those indices where only one value is provided, the index makes use of the deflections value corresponding to that radial distance as well as the deflection at a radial distance of zero or, if it includes the letter "m," at the radial distance where the maximum deflection occurs, which is not necessarily zero. The only exception is the Area Under the Pavement Profile (AUPP) Index, which is based on the deflections measured at 0, 12, 24, and 26 inches (0, 304.8, 609.6, and 660.4 mm) from the load center. The equations for each index are provided in the corresponding report.⁽¹⁾

Of the indices listed in table 2, Horak's radius of curvature equation (R2₁₂) seemed to be the overall best index for two reasons: (1) its R² was greater than 0.9 and (2) it was minimally affected by the AC thickness. The SCIm₈ Index is also a promising index regardless of AC thickness. Other appropriate indices included the Radius of Curvature (both R1₁₂ and R2₁₈), SCI₁₂, and SD₁₂, but unlike R2₁₂ and SCIm₈, these were dependent on AC thickness.

To confirm the adequacy, applicability, and validity of the indices, Monte Carlo simulations were conducted using a JULEA-generated database of 15,000 pavement structures covering a wide range of layer moduli and thicknesses.⁽³⁾ Surface deflections and horizontal strains at the bottom of the AC layer were computed for each pavement structure. The database was first used to identify the most sensitive pavement properties that affect the critical responses. It was then used to identify the most sensitive index that correlated well with the critical responses. From the results of the Monte Carlo simulations, SCI₈ and SCI₁₈ were initially recommended for pavement structures with known AC layer thicknesses, while R2₁₂ was recommended for pavement structures with unknown AC layer thicknesses.

To ensure the adequacy of the recommended indices, the TSD accuracy and precision results from the MnROAD field trials were used to assess their practicality and robustness. Only TSD data were used since the RWD deflections were limited to only two points. For accuracy, the indices were compared with those from the deflection basins measured with geophone 3 at the MnROAD cells. Accuracy was evaluated in terms of the percentage of difference for the deflection indices. For precision, SEE values and ranges were estimated for each index and each MnROAD cell. The median coefficient of variation (COV) (ratio between median SEE and median range) was used to quantify the precision of each deflection index.

The accuracy and precision results were then combined in a plot segmented into four quadrants based on 15 percent median difference and 15 percent median COV limits (see figure 10). The most robust indices are those in the lower left quadrant shaded in green, and they include four DSIs, TS₄, and AUPP. The indices in the upper left quadrant (e.g., TS₈, TS₁₂, and SCI₁₂) may also be considered as reasonably precise but not as accurate as those in the lower left quadrant. In addition, the three radii of curvature indices are in the upper right quadrant shaded in red; therefore, they are considered less accurate and less precise as compared to those in the lower left quadrant.

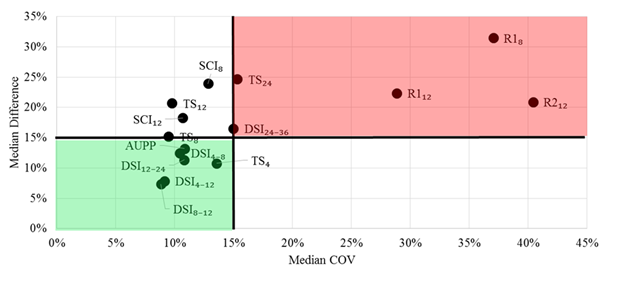
Figure 10. Graph. Overall field performance of indices.

The recommended indices were then ranked according to overall performance. The device precision, device accuracy, and model uncertainties (ratio of SEE to mean range of calculated strains) were assigned values of 1 (poor) when their values were greater than 20 percent, 3 (fair) when their values were between 10 and 20 percent, and 5 (good) for values less than 10 percent. Similarly, the R² values were assigned values of 1 (poor) for values less than 0.90, 3 (fair) for values between 0.90 and 0.95, and 5 (good) for values above 0.95. Equal weights (25 percent) were assigned to the four parameters to obtain an overall performance score for the promising indices.

The complete set of recommended indices are listed in table 3. As shown, DSI_{4 - 12} (difference between deflections at 4 and 12 inches (101.6 and 304.8 mm) from load), which was formulated as part of the study, was found to be the most appropriate index, regardless of AC thickness, and hence it is recommended for use in network-level PMS applications. SCI₁₂ (difference between deflections at 0 and 12 inches (0 and 304.8 mm) from load) performed nearly as well, and hence it could also be considered. Regardless of the index selected, it is important for users to understand the range of conditions that affected the accuracy and precision evaluation of the TSD and hence the aptness of the recommended indices.

1 inch = 25.4 mm

IMPLEMENTATION OF FINDINGS

The identification of indices that best relate deflections measured by TSDDs to horizontal strains at the bottom of the AC layer is an important step toward the use of these devices and indices in support of network-level PMS applications, but additional steps are needed. For example, how are the horizontal strains computed at the bottom of the AC layer based on the measured deflection(s) to be used to assess the structural capacity of pavements? This and other network-level PMS implementation considerations are addressed in this section.

While different approaches are possible, the one illustrated in figure 11 is recommended for network-level PMS applications and decisionmaking. In this approach, the decisions based on the traditional pavement condition metrics are confirmed and/or adjusted based on the TSDD measurements. This enables the pavement community an opportunity to gradually implement TSDD measurements while avoiding abrupt changes to their institutional approaches.

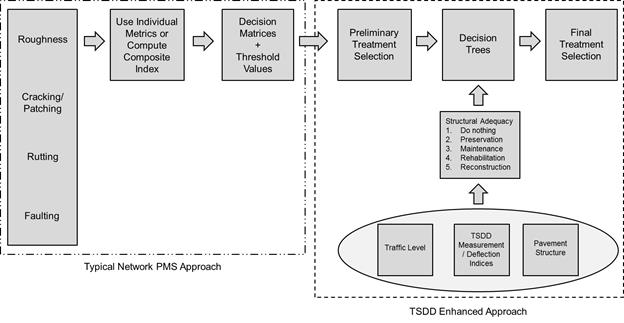
Figure 11. Flowchart. Idealized PMS containing a TSDD structural evaluation component.

To deliver a robust system, the level of sophistication of the analysis should be balanced with the uncertainties of the TSDDs. Accordingly, factors such as accuracy and precision of measurements, TSDD operation parameters, and availability of additional information, such as pavement structure, traffic, and loadings, were considered in proposing the incorporation of TSDD measurements into network-level PMS applications. In turn, the incorporation of TSDDs into network-level PMS applications can be summarized in the following steps:

1. Calculate representative indices for estimating structural condition of pavement: As stated earlier, the most feasible parameters are DSI and SCI considering fatigue cracking as the critical parameter.
   
   
2. Estimate horizontal strains at bottom of AC layer: This can be done using recommended or user selected deflection index (see table 3).
   
   
3. Adjust the estimated strains to a standard temperature: The strains computed in step 2 need to be corrected to a standard reference temperature for consistent evaluation and tracking of the deflection indices over time. Assuming a standard reference temperature of 70 °F (21.11 °C), the recommended approach, developed as part of the study, is to: (1) compute a temperature correction factor based on the temperature at time of the TSDD field measurements and a reference temperature of 70 °F (21.11 °C), (2) compute the AC dynamic modulus based on the strains computed in step 2 and the AC layer thickness, (3) compute the AC dynamic modulus at the reference temperature of 70 °F (21.11 °C), and (4) compute the temperature corrected strains using the AC modulus at the reference temperature of 70 °F (21.11 °C). Detailed steps are provided in the corresponding report.⁽¹⁾
   
   
4.   Establish structural adequacy of pavements using temperature corrected strain: Ideally, it is desirable to be able to determine whether different segments of a pavement network are candidates for either preservation, maintenance, rehabilitation, or reconstruction or whether they are adequate in their current condition. At a minimum, the algorithm associated with this step needs to be able to provide information on whether the pavement is structurally sound for the anticipated traffic or not. The initial work toward this goal can be found in Thyagarajan et al., among others.^(4,5) Abdallah et al. suggested probabilistic methods for this purpose as applied to FWD using artificial neural networks.⁽⁶⁾ These and similar work by other researchers should be pursued.

Besides these four steps, another critical consideration in the incorporation of TSDDs into network-level structural evaluations is the spatial averaging of the data. For effective utilization, spatial statistical analysis and segmentation of the TSDD data are necessary. A statistical tool is needed that enables pavement engineers to distinguish changes in the road segments due to either changes in the pavement structure or the deterioration of the pavement sections and considers the capabilities of the TSDD as well as the condition and nature of the pavement structures. In the short term, a probabilistic structural analysis can be incorporated for segmentation of the roads at the network level. In the medium and long terms, a dynamic and adaptive optimization can be added to assist decisionmakers.

Another important consideration is the requirement for additional information to enable more rigorous structural evaluations. This information includes best estimates of pavement structures (and in particular the AC layer thickness), functional condition of the pavements (including IRI and extent of cracking) to check and/or to help rationalize the results, best estimates of present and future traffic, and ambient condition at the time of testing. It is also desirable that tools be added to the TSDDs by the manufacturers and/or owners to measure these data.

CONCLUSIONS AND OTHER RECOMMENDATIONS

This section summarizes the major findings, conclusions, and recommendations of the FHWA-sponsored study to establish a reliable measure of pavement structural condition based on traffic speed deflection technology. TSDD testing has advanced over the past decade, and the technology of these devices—the RWD and TSD—provides reasonable accurate and precise pavement response measurements. Data analyses have shown that indices that can be derived from TSD measurements provide a robust assessment of pavement structural conditions at the network level. Improvements in the number of sensors and their locations are needed to use the recommended analysis methodologies with the RWD, but these should not be difficult to achieve.

The initial recommended implementation steps were detailed in the previous section, but these steps need to be taken from concept to full implementation. Similarly, the validation and/or calibration of the recommended deflection indices as well as implementation procedures need to be performed using field data collected on highway agency networks. Significant equipment improvements are also possible. For example, measurements of deflection parameters at two or more points (i.e., basins) as well as the load characteristics applied to the pavement during testing will enable more robust analyses.

The data collected by TSDDs were averaged over distance. Averaging was done over 0.1-mi (0.161-km) intervals for the RWD and over 32.8-ft (10-m) intervals for the TSD. The shorter the averaging distance is, the more detailed the analysis will be. Averaging is necessary for SHAs to work with a manageable amount of data. Accordingly, in the short term, it is desirable for manufacturers to report not only the mean deflection parameters but also other statistical information so that analysts can judge the level of variability associated with the data. In the medium term, the level of uncertainties in the measured deflection parameters should be verified through independent research. In the long term, it is desirable that averaging be done as part of the analysis and not the data collection.

In addition, several future research studies are recommended, including (1) confirming the predictive power of the recommended deflection indices through the use of measurements taken by strain gauges at the bottom of the AC layer during TSDD loadings, (2) expanding and validating the prediction of subgrade strain to complement horizontal strains at the bottom of the AC layer, (3) applying TSDDs to PCC pavements to evaluate their applicability to network-level pavement evaluations, including load transfer and joint condition, (4) conducting a more indepth study of the impact of ambient and pavement structure conditions on the deflection measurements for more robust guidelines, and (5) determining methodologies for the development of structural performance curves for prediction of future condition from TSDD-derived structural indices measured over time.

REFERENCES

1. Rada, G.R., Nazarian, S., Visintine, B.A., Siddharthan, R., and Thyagarajan, S. (2015). Pavement Structural Evaluation at the Network Level, Report No. FHWA-HRT-15-074, Federal Highway Administration, Washington, DC.
   
   
2. Siddharthan, R.V., Yao, J., and Sebaaly, P.E. (1998). "Pavement Strain From Moving Dynamic 3-D Load Distribution," Journal of Transportation Engineering, 124(6), 557-566.
   
   
3. Uzan, J. (undated). JULEA: Jacob Uzan Layered Elastic Analysis, Technion University, Haifa, Israel.
   
   
4. Thyagarajan, S., Sivaneswaran, N., Petros, K., and Muhunthan, B. (2011). Development of a Simplified Method for Interpreting Surface Deflections for In-Service Flexible Pavement Evaluation, 8th International Conference on Managing Pavement Assets, Santiago, Chile.
   
   
5. Thyagarajan, S., Sivaneswaran, N., and Petros, K. (2015). "Incorporating Traffic Speed Deflection Devices in Structural Evaluation of Flexible Pavement: Methodologies for Pavement Management Application," Transportation Research Record 2523, 72-79, Transportation Research Board, Washington, DC.
   
   
6. Abdallah, I., Melchor-Lucero, O., Ferregut, C., and Nazarian, S. (2000). Development of a Comprehensive, Rational Method for Determination of Remaining Life of an Existing Pavement, Report No. TX-99/1711-2, Texas Department of Transportation, Austin, TX.