U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| Report |
| This report is an archived publication and may contain dated technical, contact, and link information |
| Publication Number: FHWA-HRT-12-025 Date: June 2012 |
Publication Number: FHWA-HRT-12-025 Date: June 2012 |
PDF files can be viewed with the Acrobat® Reader®
The objective of this study was to develop an approach for incorporating techniques used to interpret and evaluate deflection data for network-level pavement management system (PMS) applications. The first part of this research focused on identifying and evaluating existing techniques, seeking out those that were simple, reliable, and easy to incorporate into current PMS practices, as well as those that produced consistent results. The second part of the research detailed the development of guidelines for the application of recommended techniques and procedures for determining optimum falling weight deflectometer (FWD) test spacing and data collection frequency. While there are many viable techniques available for evaluating the structural capacity of pavements that use FWD for project-level analysis, many of these techniques are time consuming and require an experienced analyst. As a result, using pavement deflection testing for network-level analysis has been limited to date. This guide contains step-by-step instructions for applying appropriate evaluation techniques for network-level (not project-level) measurements and analyses.
Jorge
E. Pagán-Ortiz
Director,
Office of Infrastructure
Research
and Development
Notice
This document is disseminated under the sponsorship of the U.S. Department of Transportation in the interest of information exchange. The U.S. Government assumes no liability for the use of the information contained in this document. This report does not constitute a standard, specification, or regulation.
The U.S. Government does not endorse products or manufacturers. Trademarks or manufacturers' names appear in this report only because they are considered essential to the objective of the document.
Quality Assurance Statement
The Federal Highway Administration (FHWA) provides high-quality information to serve Government, industry, and the public in a manner that promotes public understanding. Standards and policies are used to ensure and maximize the quality, objectivity, utility, and integrity of its information. FHWA periodically reviews quality issues and adjusts its programs and processes to ensure continuous quality improvement.
1. Report No. FHWA-HRT-12-025 |
2. Government Accession No. |
3. Recipient's Catalog No. |
||||
4. Title and Subtitle Simplified Techniques for Evaluation and Interpretation of Pavement Deflections for Network-Level Analysis: Guide for Assessment of Pavement Structure Performance for PMS Applications |
5. Report Date June 2012 |
|||||
6. Performing Organization Code |
||||||
7. Author(s) R. Stubstad, R. Carvalho, R. Briggs, and O. Selezneva |
8. Performing Organization Report No. |
|||||
9. Performing Organization Name and Address Applied Research Associates, Inc. 7184 Troy Hill Drive, Suite N Elkridge, MD 21075-7056 |
10. Work Unit No. (TRAIS) |
|||||
11. Contract or Grant No. DTFH61-02-C-00138 |
||||||
12. Sponsoring Agency Name and Address Office of Infrastructure Research and Development Federal Highway Administration 6300 Georgetown Pike McLean, VA 22101-2296 |
13. Type of Report and Period Covered Guide |
|||||
14. Sponsoring Agency Code |
||||||
15. Supplementary Notes The Contracting Officer's Technical Representative (COTR) was Larry Wiser, HRDI-30. |
||||||
16. Abstract The objective of this study was to develop an approach for incorporating techniques to interpret and evaluate deflection data for network-level pavement management system (PMS) applications. The first part of this research focused on identifying and evaluating existing techniques, seeking out those that were simple, reliable, and easy to incorporate into current PMS practices, as well as those that produced consistent results. The second part of the research detailed the development of guidelines for the application of recommended techniques and procedures for determining optimum falling weight deflectometer (FWD) test spacing and data collection frequency. While there are many viable techniques available for evaluating the structural capacity of pavements that use FWD for project-level analysis, many of these techniques are time consuming and require an experienced analyst. As a result, using pavement deflection testing for network-level analysis has been limited to date. This guide provides information for the assessment of pavement structural performance for PMS applications. It reflects the general findings presented in the accompanying final report, Simplified Techniques for Evaluation and Interpretation of Pavement Deflections for Network-Level Analysis (FHWA-HRT-12-023). |
||||||
17. Key Words Pavement performance, Rehabilitation, Maintenance, Pavement design, Long-term performance, Flexible pavements, Rigid pavements |
18. Distribution Statement No restrictions. This document is available to the public through the National Technical Information Service, Springfield, VA 22161. |
|||||
19. Security Classification (of this report) Unclassified |
20. Security Classification (of this page) Unclassified |
21. No. of Pages 33 |
22. Price |
|||
Form DOT F 1700.7 (8-72) Reproduction of completed page authorized
SI* (Modern Metric) Conversion Factors
This guide can be used to characterize the overall level of a pavement's structural characteristics for network-level analyses using falling weight deflectometers (FWDs) or heavy weight deflectometers (HWDs). The deflection data are coupled with other readily available input and pavement performance data that can be used to characterize the overall level of the pavement structural characteristics for pavement management applications. This guide contains step-by-step instructions for applying appropriate evaluation techniques for network-level (not project-level) measurements and analyses. An example of an application of this approach to a pavement network sample is provided in the final report, Simplified Techniques for Evaluation and Interpretation of Pavement Deflections for Network-Level Analysis.(1)
Applicable measurement and analysis techniques for assessing the overall network-level structural performance of roadways only include the use of load deflection data obtained by the commonly used FWD. An HWD can also be used at its lower load levels corresponding to typical truck axle loads on highway and roadway pavements. While it is possible that currently available or future high-speed load-deflection measurement devices (i.e., the experimental rolling wheel deflectometer) may be used as well, the data obtained with these newer devices are not considered in these guidelines.
The input data required for the addition of a structural component to an agency's pavement management system (PMS) include data normally present in an agency's PMS in addition to FWD or HWD load deflection data taken at appropriate spatial and temporal intervals system-wide. Preprocessing of these data is not required other than the usual quality control checks for FWD field errors, such as misstated sensor positions, faulty deflection sensors or load cells, and/or other data entry errors from field testing.
The development effort for these guidelines utilized data from the over 20-year-old Strategic Highway Research Program (SHRP) experimental test program. For this reason, the original seven SHRP sensor positions were used to perform the data analyses required (i.e., 0, 8, 12, 18, 24, 36, and 60 inches (0, 200, 300, 450, 600, 900, and 1,500 mm)).(2) Since only interior or center slab tests were utilized to develop the method for reasons described in the following sections, the same sensor positions were used for concrete as well as asphalt pavements.
A list of required sensor positions covering four flexible pavement and three rigid concrete pavement distress types described in this guide are shown in table 1.
Table 1. Required FWD or HWD sensor positions to utilize the FWD at the network level.
| Sensor Position | Flexible Pavements | Rigid Pavements |
|---|---|---|
| 0 inches (0 mm) | X | |
| 8 inches (200 mm) | X | |
| 12 inches (300 mm) | X | |
| 18 inches (450 mm) | X | X |
| 24 inches (600 mm) | X | |
| 36 inches (900 mm) | X |
Note: For rigid pavements, only interior or center slabs were tested.
Due to many issues, including the propensity of concrete pavements to warp and curl, joint tests are not recommended for network-level testing since they would require a stringent time window within which testing would have to occur. Moreover, studies of the Federal Highway Administration's (FHWA) Long-Term Pavement Performance (LTPP) database provided no improvement in the derived stochastic relationships when joint tests (e.g., load transfer efficiency (LTE)) were included in the analyses.(3) Lastly, the acceptable time window for interior slab testing is much longer than for joint testing, making the simple approach of applying FWD load deflection data to a network database easier to carry out in the field.
As can be seen in table 1, the most efficient way to proceed for network-level FWD testing is to use the original SHRP configuration of sensor positions (0, 8, 12, 18, 24, and 36 inches (0, 200, 300, 450, 600, and 900 mm)) for the first six sensors. These six sensor positions cover both flexible pavement and rigid pavement tests taken at an interior position for jointed concrete pavements. Additional FWD/HWD deflection readings should also be taken to cover other potential uses of FWD load deflection data, such as LTE for rigid pavement tests at joints with a trailing sensor and/or additional sensors placed further from the load plate than the requisite 36 inches (900 mm) for all pavements.
The only required test load for flexible pavements is 9,000 lbf (40 kN) within ±10 percent. For rigid pavements, the required test load is either 9,000 or 12,000 lbf (40 or 53 kN) within±10 percent depending on an agency's normal deflection testing practices for rigid pavements. In any event, the deflections have to be normalized (scaled up or down) to the target load level in an agency's analysis package of choice.
In this guide, only the 9,000-lbf (40-kN) rigid pavement loading relationships are shown. However, in the final report, equally positive relationships also exist for the nominal 12,000-lbf (53-kN) load level on concrete pavements if that load level is preferred by the agency.
In order to implement a network-level structural analysis component in a PMS enhanced with FWD tests using a stochastic model, the following data elements are needed:
The three flexible pavement distress types and the three rigid pavement distress types (with overlap) in the suggested stochastic models include the following:
By implication and based on the above list of pavement distresses included in this guide, composite pavements and continuously reinforced concrete pavements were not included due to a lack of historical data.
The appropriate analysis technique for use with network-level load-deflection data depends on the pavement type and the type of distress the PMS user wishes to use to characterize structural condition. At a minimum, it is recommended that the typical distresses observed on the local network are used. If this information is not available, the analysis should be conducted using all applicable models as described in this section.
For almost all agencies, system-wide load deflection data are not available. Therefore, it is recommended that the so-called "global" relationships and threshold values derived through the methodology should be used until local calibration of these relationships can take place, which could take as long as 5 years. Local calibration will significantly improve the accuracy of these models, as reported in the accompanying final report.(1)
It should be noted that the methodology developed was based on data obtained from FWD tests conducted along typical State and interstate highways, expressways, and freeways during the SHRP LTPP study. Therefore, it is possible that an agency with lighter-duty pavements will find that the threshold and cutoff values initially derived through the equations presented in the following sections may not be appropriate for every existing PMS, whether in the United States or elsewhere. This will eventually be mitigated by the use of traffic levels.
The general approach recommended in this guide only provides one additional link in an otherwise incomplete pavement management database and should only be used as a planning tool to assist network pavement engineers in predicting the likelihood of the development of pavement distress levels. As a result, there is a need for future structural improvement to the network as a whole, not every maintenance and rehabilitation project on an individual basis. This is accomplished through the use of a stochastic approach to evaluate FWD load deflection data called the "logistic model," which is discussed in the following section.
The objective of a pavement design is to provide a structure that will exhibit adequate structural performance throughout its design life. It is expected that the structural condition affects the rate the pavement deteriorates over time. By definition, a given pavement structure exhibits acceptable performance if distress levels do not exceed their threshold values during a given period of time (e.g., fatigue cracking should not exceed 25 percent of the total area within the first 15 years of service).
Logistic models describe the probability of an event being acceptable or not acceptable as a function of a predictor variable. Therefore, they can be used to establish a link between performance and structural condition by modeling the probability of acceptable performance using measurements of deflections and parameters (techniques) computed from FWD or HWD deflection basins.
The goal of the stochastic approach is to use the probability density function from the logistic model to obtain insightful probability information about the pavement structural condition required to achieve the desired performance during a desirable (design) period of time. This new network-level information obtained from the FWD can then be used to define strategic treatments (maintenance or rehabilitation) to be used in the PMS optimization process.
A typical logistic model probability function is shown in figure 1. It describes the likelihood of a pavement section exhibiting acceptable performance (measured in terms of one particular distress) as a function of a given deflection parameter called "predictor variable X." The limit between acceptable and not acceptable performance is given by a parameter called the "cutoff." The cutoff value is computed as part of the model calibration process using the receiver operating characteristics (ROC) curve analysis. (See chapter 4 in the final report.(1))
The probability density function is used to determine the thresholds that define structural condition. By definition, the cutoff value in a logistic model determines how to convert the continuous probability prediction as a dichotomous outcome (i.e., predicted probabilities above the threshold are defined as acceptable while others are defined as not acceptable). In addition to the cutoff threshold, other values can be defined to further enhance the structural analysis. For example, figure 1 describes a second threshold created at a probability of 0.4, and it is used to differentiate sections with fair structural condition from poor ones. It is recommended that the second threshold be initially defined as one-half of the cutoff value. Note that this definition is arbitrary and can be adjusted to better fit an agency's rehabilitation practices or network characteristics.
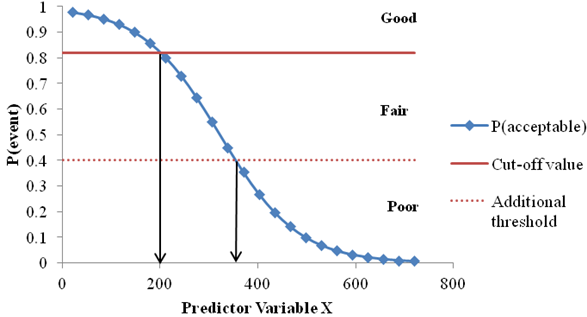
Figure 1. Graph. Typical logistic model probability function of predictor variable X.
Once thresholds and their respective deflection parameters are identified, a structural decision matrix (also referred to as a structural rehabilitation matrix) can be generated. Table 2 shows the structural decision matrix obtained from the probability density function in figure 1. After the structural decision matrix has been established, it can be incorporated into the PMS and used in the analysis in a fashion similar to the functional decision matrix to prescribe maintenance and rehabilitation strategies.
Table 2. Example of structural decision matrix.
| Structural Condition | Deflection Parameter |
|---|---|
| Good | < 200 |
| Fair | 200-350 |
| Poor | > 350 |
The deflection parameter used to stochastically predict
![]()
Figure 2. Equation. General formulation of the logistic model.
![]()
Figure 3. Equation. General linear formulation for the exponent term of the logistic model.
The input variables needed to utilize the flexible pavement roughness model are as follows:
The most accurate roughness (IRI) model identified for flexible pavements is represented by the equations in figure 2 and figure 3 utilizing the variable values shown in table 3.
Table 3. Variables in the I2 final model for flexible pavements based on roughness performance.
| Variables (bi) | ai | p-value |
|---|---|---|
| I2 | 239.849 | 0.000005706 |
| Current life | -0.189 | 0.01174 |
| Class 9 volume | -0.0006781 | 0.0001037 |
| Constant | 0.8375 | 0.01071 |
| Cutoff | 0.812 | |
bi = Load
transfer efficiency.
ai = Variables presented in figure 3.
Ii = Reciprocal indicator for the ith deflection
value.
The variable I2 in table 3 is calculated using the equation in figure 4.
![]()
Figure 4. Equation. Calculation of I2.
Where D2 is the deflection 8 inches (200 mm) from the center of the FWD load plate.
The accuracy in logistic models is computed based on the ROC curve. The area under the ROC curve provides the accuracy of the model, which can be considered the equivalent of the R2 value used for linear models. In addition to accuracy, the ROC curve also provides the threshold that defines how the results from the probability density function are interpreted in a binary system (i.e., the threshold used to separate probabilities that are referred to acceptable and not acceptable). This threshold is called the cutoff value. For the model described in table 3 and figure 4, the accuracy is 0.72, and the cutoff value is 0.812.
The input variables needed to utilize the flexible pavement rutting model are as follows:
The most accurate rutting model identified for flexible pavements utilizes the variable values in table 4 and the equation in figure 5.
Table 4. Variables in the CI3 final model for flexible pavements based on rutting performance.
| Variables (bi) | ai | p-value |
|---|---|---|
| CI3 | -0.01146 | 0.00001594 |
| Precipitation (mm) | -0.0005259 | 0.04018 |
| Class 9 volume | -0.0007688 | 0.00005421 |
| Constant | 2.6586 | 1.0136 x 10-13 |
| Cutoff | 0.792 | |
bi = Load
transfer efficiency.
ai = Variables presented in figure 3.
CIi = Curvature index for the ith
deflection value.
1 inch = 25.4 mm
The variable CI3 in table 4 is calculated using the equation in figure 5.
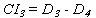
Figure 5. Equation. Calculation of CI3.
Where D3 is the deflection 12 inches (300 mm) from the center of the FWD load plate and D4 is the deflection 18 inches (450 mm) from the center of the FWD load plate. The accuracy as measured by the area under the ROC curve is 0.66, and the cutoff value is 0.792.
The input variables needed to utilize the flexible pavement fatigue cracking model are as follows:
The most accurate fatigue cracking model utilizes the equations in figure 2 and figure 3 with the variable values in table 5.
Table 5. Variables in the I1 final model for flexible pavements based on fatigue cracking performance.
| Variables (bi) | ai | p-value |
|---|---|---|
| I1 | 154.764 | 0.0006015 |
| AADTT | -0.0005073 | 0.0007847 |
| Pavement type | 0.3774 | 0.07598 |
| Constant | -0.2202 | 0.4422 |
| Cutoff | 0.605 | |
bi = Load
transfer efficiency.
ai = Variables presented in figure 3.
Ii = Reciprocal indicator for the ith deflection value.
The variable I1 in table 5 is calculated using the equation in figure 6.
![]()
Figure 6. Equation. Calculation of I1.
Where D1 is the deflection at the center of the FWD load plate. The accuracy as measured by the area under the ROC curve is 0.72, and the cutoff value is 0.605.
Two sets of models have been developed for rigid pavements-one for a target FWD load of 9,000 lbf (40 kN) and one for a target load of 12,000 lbf (53 kN). The overall accuracy of the 9,000-lbf (40-kN) load relationships are at least as good as the relationships for the 12,000-lbf (53-kN) FWD load level. Accordingly, only the 9,000-lbf (40-kN) equations are shown in this section. Agencies that generally use a 12,000-lbf (53-kN) FWD load level for rigid pavements should refer to the final report for additional information.(1)
The input variables needed to utilize the rigid pavement roughness model are as follows:
The most accurate roughness (IRI) model identified for rigid pavements is represented by the equation in figure 3 using the variable values in table 6.
Table 6. Variables in the CI5 final model for rigid pavements based on roughness performance.
| Variables (bi) | ai | p-value |
|---|---|---|
| CI5 | -0.078 | 0.00406 |
| Class 9 volume | -0.0003877 | 0.115 |
| Constant | 2.057 | 0.00002168 |
| Cutoff | 0.665 | |
bi = Load
transfer efficiency.
ai = Variables presented in figure 3.
CIi = Curvature index for the ith
deflection value.
The variable CI5 in table 6 is calculated using the equation in figure 7.
![]()
Figure 7. Equation. Calculation of CI5.
Where D5 is the deflection 24 inches (600 mm) from the center of the FWD load plate and D6 is the deflection 36 inches (900 mm) from the center of the FWD load plate. The accuracy as measured by the area under the ROC curve is 0.65, and the cutoff value is 0.665.
The input variables needed to utilize the rigid pavement joint faulting model are as follows:
The most accurate joint faulting (i.e., step faulting) model identified for rigid pavements is represented by the equations in figure 2 and figure 3 using the variable values in table 7.
Table 7. Variables in the D6 final model for rigid pavements based on faulting at joints performance.
| Variables (bi) | ai | p-value |
|---|---|---|
| D6 | -0.009225 | 0.138 |
| Subgrade type | -0.495 | 0.2003 |
| Constant | 1.499 | 0.005818 |
| Cutoff | 0.635 | |
bi = Load
transfer efficiency.
ai = Variables presented in figure 3.
Where D6 is the deflection 36 inches (900 mm) from the center of the FWD load plate. The accuracy as measured by the area under the ROC curve is 0.64, and the cutoff value is 0.635.
The input variables needed to utilize the rigid pavement transverse slab cracking model are as follows:
The most accurate transverse slab cracking model identified for rigid pavements is represented by the equations in figure 2 and figure 3 using the variable values in table 8.
Table 8. Variables in the CI4 final model for rigid pavements based on transverse slab cracking performance.
| Variables (bi) | ai | p-value |
|---|---|---|
| CI4 | -0.254 | 0.0003759 |
| Class 9 volume | -0.001012 | 0.001084 |
| Constant | 3.630 | 0.0000003134 |
| Cutoff | 0.7 | |
bi = Load
transfer efficiency.
ai = Variables presented in figure 3.
CIi = Curvature index for the ith
deflection value.
The value for CI4 in table 8 is calculated using the equation in figure 8.
![]()
Figure 8. Equation. Calculation of CI4.
The accuracy as measured by the area under the ROC curve is 0.77, and the cutoff value is 0.70.
Optimum test spacings for FWD measurements are a function of the criteria used to determine what "optimal" means. One approach is to use statistical methods to determine the minimum number of deflection measurements that accurately (i.e., within an acceptable level of error) reflect the true structural condition of the entire highway segment in question. Another approach is to collect as much information as the budget, equipment, human resources, and allotted time will allow while minimizing risk to the travelling public and equipment operators.
Table 9 can be used to calculate the expected error in the average deflection as a result of a selected sampling strategy (spacing) for a given section length at a 90 percent reliability level.
Table 9. Errors in percentage for 90 percent reliability based on various section lengths, sample spacings, and coefficient of variation of 33 percent.
| Probability | Length (mile) | Spacing (mile) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | ||
| 90 percent | 1 | 14.18 | 17.94 | 21.24 | 24.22 | 26.98 | 29.57 | 32.02 | 34.35 | 36.59 |
| 2 | 10.10 | 12.71 | 14.98 | 17.03 | 18.93 | 20.70 | 22.37 | 23.96 | 25.48 | |
| 3 | 8.28 | 10.38 | 12.21 | 13.86 | 15.38 | 16.80 | 18.13 | 19.41 | 20.62 | |
| 4 | 7.19 | 9.00 | 10.56 | 11.97 | 13.27 | 14.48 | 15.63 | 16.71 | 17.75 | |
| 5 | 6.44 | 8.05 | 9.44 | 10.69 | 11.84 | 12.91 | 13.92 | 14.88 | 15.80 | |
| 6 | 5.89 | 7.35 | 8.61 | 9.74 | 10.78 | 11.75 | 12.67 | 13.54 | 14.36 | |
| 7 | 5.46 | 6.80 | 7.97 | 9.01 | 9.97 | 10.86 | 11.70 | 12.49 | 13.25 | |
| 8 | 5.11 | 6.36 | 7.45 | 8.42 | 9.31 | 10.14 | 10.92 | 11.66 | 12.36 | |
| 9 | 4.82 | 6.00 | 7.02 | 7.93 | 8.76 | 9.54 | 10.27 | 10.96 | 11.62 | |
| 10 | 4.58 | 5.69 | 6.65 | 7.51 | 8.30 | 9.03 | 9.72 | 10.38 | 11.00 | |
1 mi = 1.61 km
Table 9 shows that if 10 10-mi (16.1-km) highway segments are tested at 0.2-mi (0.322-km) intervals, the average of the deflections measured in each section will be within ±4.58 percent of their true value for 9 of the 10 sections.
Practical considerations, such as access to the facilities (due to traffic or other factors), might force an agency to adopt wider test point spacings. If so, table 9 can be used to quantify the additional error in measurement accuracy. The main point to take away from this is that an agency should do what is reasonably possible under their own specific circumstances; if a less than desirable test spacing interval is all that is possible, it is better than nothing at all and will generally provide reasonable results for network-level applications.
There are two seasonal pavement conditions during which deflection testing should be avoided: frozen pavements and spring thaw. Neither of these conditions produces pavement deflections that are representative of the pavement response at most other times of the year. Agencies should conduct seasonal testing to determine when these occur and how long they last and then avoid collecting measurements during these times.
Analysis of LTPP deflection data collected over many years indicates that flexible pavements can be tested at the network level at 5-year cycles. Rigid pavements may be tested at up to 10-year intervals.
The process for selecting the best fitting technique for local calibration is relatively simple. A complete example of calibration is described in chapter 4 of the final report.(1) A summary of the steps is provided in this section.
The process for selecting the best model consists of the following steps:
Data availability is important. Logistic regression models are obtained from the statistical analysis of several independent variables that potentially have an impact on pavement performance. Initially, no variable should be eliminated without being properly assessed. Typical groups of variables include deflection, structure, traffic, climate, and performance. It is important that any available variable in these categories is used; however, dependent variables that are directly related to each other (interdependent) should be avoided.
Deflections obtained from FWD testing are used to compute deflection parameters to be used as independent variables in the logistic model. A detailed literature review of the most used and more successful applications was carried out as part of this research and is described in chapter 3 in the final report.(1)
It is recommended that thickness and material type be used as structure variables. In addition, two dichotomous variables based on the structure characteristics are recommended: one related to the subgrade type (coarse or fine) and the other related to the base type (bound or unbound).
It is recommended that traffic data be limited to truck volume using AADTT and the volume of the two most predominant classes, classes 5 and 9 in the FHWA truck classification system.
For climate conditions, two variables are recommended: precipitation and temperature. For simplification, annual averages can be used for both. It is expected that there will not be significant variations in climatic conditions for local calibration. If that is the case, climatic variables may be excluded from the analysis.
The main characteristic of a logistic model is the prediction of the probability of an event occurring given a set of independent variables. The assumption is that the rate of deterioration increases as the structural condition worsens, and the probability of a pavement failing prematurely can be calculated based on a combination of deflection parameters and site characteristics. Therefore, pavement performance must be transformed in a dichotomous variable representing the occurrence of this event (acceptable performance after a number of years of service). Service life can be arbitrarily chosen or estimated to reflect the expected performance in the network as a whole.
The calibration and evaluation of selected deflection techniques are based on the logistic model approach and the notion that the best deflection analysis techniques yield the most accurate models. Each deflection parameter available can be used to develop a logistic model for each performance measure in the dataset. A statistical package should be used to expedite the process, although a spreadsheet can be used to program the optimization algorithm. The general formulation of the logistic model is shown in figure 2 and figure 3.
The model's exponent, b, is calibrated to minimize the false positives and false negatives in the probability analysis. The significance of each variable is computed, and the least significant variable is removed from the calculation. This process continues until no improvement in accuracy can be made or the maximum number of iterations is achieved.
Logistic model accuracy is best evaluated through an analysis of an ROC curve, which allows researchers to select possibly optimal models and discard suboptimal ones independently from the class distribution of the predictor. An example of an ROC curve is provided in figure 9.
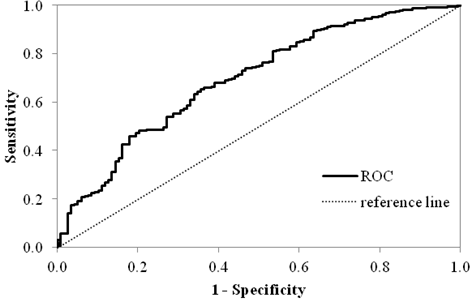
Figure 9. Graph. Example of an ROC curve.
The ROC curve is drawn using the true positive rate (TPR) and false positive rate (FPR). TPR is determined by the number of true positive predictions normalized by the total number of positive observed values. Conversely, FPR defines how many incorrect positive results occur among all negative samples available during the test.
The ROC space is defined by FPR and TPR as the x- and y-axes, respectively, which depict the relative trade-off between TPR and FPR. TPR is often described as the sensitivity of the model, while (1 - FPR) is often seen as the true negative rate (TNR) or specificity. Therefore, the ROC curve is also referred to as the sensitivity versus (1 - specificity) curve. Each case consisting of prediction and observed values represents one point in the ROC space. Details about the ROC curve can be found in the chapter 4 of the final report.(1)
The area under the ROC curve defines the goodness of fit of the predictions. In an analogy with measures of linear optimization techniques, the area under the ROC curve can be viewed as a stand-in for the R2 value. In addition to the goodness of fit, the ROC curve is used to define the cutoff value of the model. The cutoff is an equally important parameter that defines how the results from the probability density function can be interpreted in a binary system (i.e., the threshold used to separate probabilities are referred to as acceptable and not acceptable). The cutoff is defined as the probability value that corresponds to the point in the ROC curve closest to the perfect classification point (0,1). When the cutoff is used to convert the predicted probabilities into binary outcomes, the model yields the highest level of accuracy (i.e., highest TPR and TNR).
The last step in the analysis process is the sensitivity of the logistic models to its variables. It is important that the model produces as accurate results as possible and that the model is accompanied by reasonable probabilities with reasonable values of the deflection parameter under consideration. Plots of predicted probability versus the deflection parameter can provide valuable information about the reasonableness of the model for a given set of site characteristic variables (e.g., a high truck volume, unbound base, cold climate, etc.). If results from the sensitivity plots are unreasonable, a new model must be calibrated to eliminate unrealistic outcomes.
The sensitivity analysis is executed by evaluating the predicted probability for a variety of values of the deflection parameter governing the logistic model under consideration. The objective is to verify if reasonable deflection parameter values produce expected and not counterintuitive outcomes. Two practical examples using the logistic model are provided below.
Sensitivity Analysis with Reasonable Results
Figure 10 describes the sensitivity curve of an I2 model based on roughness performance.
In this case, the cutoff value is 0.812, which corresponds to I2 = 0.1092 1/mil (0.0043 1/![]() )
(or D2 equals 9.05 mil (232
)
(or D2 equals 9.05 mil (232![]() ).
This is a reasonable value for a well-designed, high traffic volume pavement
structure. Therefore, figure 10 indicates that flexible pavements with D2 deflections below 9.05 mil (232
).
This is a reasonable value for a well-designed, high traffic volume pavement
structure. Therefore, figure 10 indicates that flexible pavements with D2 deflections below 9.05 mil (232![]() )
have greater than 80 percent chance of exhibiting acceptable roughness
performance for the next 12 years and can be classified as good in
terms of their structural condition.
)
have greater than 80 percent chance of exhibiting acceptable roughness
performance for the next 12 years and can be classified as good in
terms of their structural condition.
Figure 10. Graph. Sensitivity of roughness acceptable probability to deflection parameter I2 for flexible pavements.
Sensitivity Analysis with Unreasonable Results
In contrast, figure 11 shows the sensitivity curve of the Hogg subgrade modulus model based on roughness. The cutoff value of 0.802 yields a Hogg value of 65,000 psi (447,850 kPa), which is very high and unreasonable for subgrade moduli. The Hogg model in this case is biased toward low probabilities of acceptable performance.
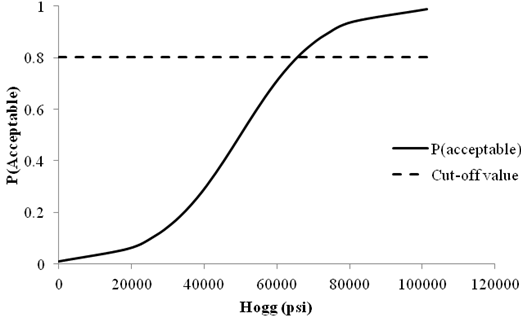
Figure 11. Graph. Sensitivity of roughness acceptable probability to deflection parameter Hogg for flexible pavements.
This type of sensitivity analysis was performed for all models developed and proved to be essential in order to rule out models that at first glance provided very good statistics but were unreasonably biased.
An example using the logistic model based on Maryland State Highway Administration data is presented in the accompanying final report.(1)