U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number: FHWA-RD-98-085 |
The AREA basin shape factor is essentially the result of numerically integrating a normalized deflection basin. When the AREA factor was first developed, test equipment generally had only four deflection sensors, which were typically spaced at one-foot intervals. Therefore, while the methodology behind the AREA factor could be applied to any test setup, by default it is calculated using sensors at 0", 12", 24" and 36" offsets, as shown in Figure 15.
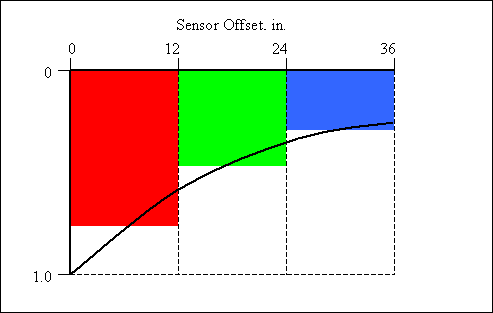
Figure 15. Graphical Representation of the AREA Factor
The AREA factor is equal to the sum of the three colored areas shown in Figure 15. The numeric expression of the AREA factor is:
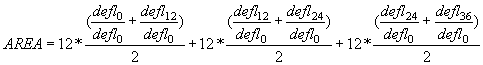
This equation simplifies to:
AREA = 6*(1 + 2*(defl12 + defl24) + defl36)/defl0
The AREA basin shape factor relates to the ratio of pavement stiffness to subgrade stiffness. The pavement stiffness characteristic here is dependent on both the thickness of the pavement structure, and on the stiffness of the materials that make up the pavement structure. The role that stiffness plays is clearly shown in Figure 18 by the relationship between AREA and pavement temperature. Increasing the thickness of the pavement would increase the AREA, whereas decreasing the thickness would decrease the AREA. Likewise, if this same pavement structure was placed on a less stiff subgrade, it would increase the AREA, or conversely, if the subgrade was stiffer, the AREA would decrease. AREA values can range from the low teens for thin soft asphalt pavements on stiff subgrade soils to the low 30s for thick stiff asphalt pavements on soft subgrade soils. If there is a hard bottom, the AREA factor will be slightly lower, depending how close to the surface is to the hard bottom.
The AREA basin factor relates inversely to the mid-depth temperature of the asphalt, that is, as the temperature goes up, the magnitude of the AREA goes down. The relationship between the mid-depth temperature of the asphalt and AREA, interestingly enough, is linear. Figure 16, Figure 17, and Figure 18 show the transform of deflection basins that were measured from one specific point on a pavement as part of the LTPP Seasonal Monitoring Program.
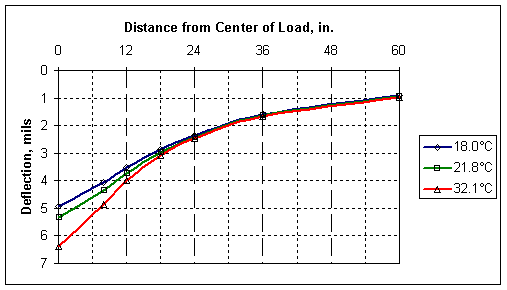
Figure 16. Sample Deflection Basins Measured at the Same Point
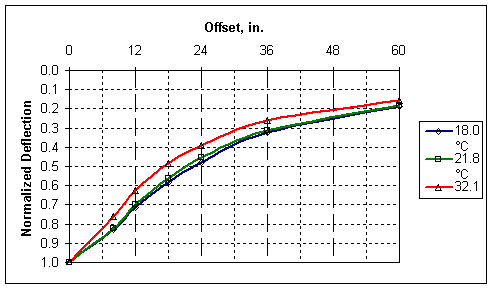
Figure 17. Deflection Basins From Figure 15 Normalized
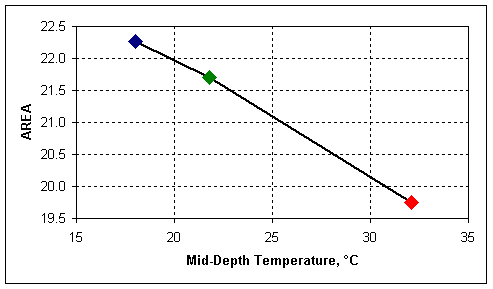
Figure 18. AREA Above the Normalized Basins in Figure 16
Figure 16 contains three basins that were measured at the same point at different times of a day as the temperature in the pavement increased. Figure 17 has plots of the same three basins, but is deflection normalized by dividing all of the basin deflections by the deflection at the center of the load plate. Figure 18 shows the relationship of the calculated AREA of the deflection basins to the measured mid-depth asphalt temperatures.
The LTPP SMP data was used to develop a regression equation that relates the AREA basin factor to pavement characteristics including the thickness of the asphalt, the temperature at the mid-depth of the asphalt, the 9 kip deflection at the 36-inch offset (which provides a replacement to the subgrade stiffness), and the latitude. (The latitude relates to the stiffness of the asphalt binder used in the mix. Hot southern climates use a stiffer binder than cooler or colder northern climates, which generally results in the asphalt mixes in colder climates being softer than asphalt mixes in warmer climates.)
The resulting regression equation for the AREA basin factor is as follows:
AREA = 13.0 + 7.77*log(ac)*log(defl36) - 6.78*log(lat)*log(defl36) + 0.105*T - 0.116*T*log(ac)
Where:
ac = Total thickness of the HMA, mmlat = Latitude of the pavement section
defl36 = Deflection (load-normalized to 40.5 kN (9 kip)) at 915 mm (36") from the center of the load plate, µm
T = Temperature at mid-depth of the HMA, °C
Source code for implementing this equation as a function in MS Excel VBA is available here.
Sample data for checking code is available here.
The AREA increases as the log of the thickness of the AC increases; decrease as the temperature of the asphalt increases because the second term with T dominates the first term with T. The latitude is a substitute for the stiffness of the binder used in the asphalt mix and the AREA decreases as the latitude increases because softer binders are used in north and harder binders are used in the south. The coefficient on the term where the latitude appears is negative, indicating that as the latitude increases, the AREA decreases which is consistent with the relationship between AREA and stiffness. The defl36 variable is in two terms where the net result of an increase in defl36 is an increase in AREA. The defl36 varies inversely with the subgrade stiffness, so as defl36 increases, the subgrade stiffness decreases and the ratio of the stiffness of the pavement to the subgrade increases.
Use of the AREA basin factor generally will require that the calculated AREA values be adjusted for temperature. Temperature adjustment factors can be calculated by using the AREA equation to calculate an AREA for the pavement tested using the mid-depth asphalt temperature at the time of the test (Tm). The AREA is then calculated again using the mid-depth asphalt temperature, or reference temperature (Tr) that it is to be adjusted to. The Basin Adjustment Factor for AREA, or BAFAREA, is the AREA at the reference temperature divided by the AREA at the measured temperature. The functions can be used to build tables of adjustment factors, or to calculate adjustment factors on a case-by-case basis.
Source code for implementing BAFAREA as a function in MS Excel VBA is available here.
Sample data for checking code is available here.