U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Federal Highway Administration > Publications > Research > Structures > A Laboratory and Field Study of Composite Piles for Bridge Substructures |
Publication Number: FHWA-HRT-04-043 |
Previous | Table of Contents | Next
In this chapter, calculations using methods commonly employed in practice are presented for the pile axial load capacity, and for the load-deflection behavior, of the three test piles at the Route 351 Bridge project. The calculations are compared with the recorded pile capacities and the measured load-deflection responses. Background information for the methodologies used to perform the analyses is also presented and discussed in this chapter.
The axial capacity of driven piles in sand is possibly the area of greatest uncertainty in foundation design (Randolph, et al., 1994), and many methods are available for predicting pile capacity. Despite the extensive amount of research in this area, the appropriateness and accuracy of current design methods are often questioned (Randolph, et al., 1994, Olson 2002). In practice it is common to use factors of safety of two, three, or more, since measured pile capacities of driven piles have been found to differ from the calculated capacities by more than three times (Olson 2002). It is expected that these uncertainties will be applicable to driven composite piles. With this in mind, the predictions for the composite piles presented in this chapter are expected to show at best a level of accuracy similar to the predictions for conventional piles.
The predictions presented herein are based primarily on design methods commonly used by U.S. highway agencies, with the exception of a relatively new method proposed by Jardine and others at the Imperial College in England; that method seems to provide a rational approach for assessing axial load capacity of driven piles (Jardine and Chow 1996).
A sketch of the axially loaded pile problem is shown in figure 147. Generally, most methods estimate the ultimate pile capacity based on consideration of vertical equilibrium of the pile at the state of incipient bearing capacity failure (i.e., when the settlement of the pile increases rapidly with little further increase in load at the pile head). From figure 147, the ultimate axial capacity of a pile is given by the equation:
where QT is the estimated ultimate axial capacity, Qs is the ultimate shaft capacity resulting from the surrounding soil in side shear, Qb is the total ultimate tip load at the base or tip of the pile (total indicates the weight of the displaced volume of soil is included), and Wp is the weight of the pile. In practice, the term Wp is usually neglected since it is considered small compared to the accuracy of the prediction of QT.
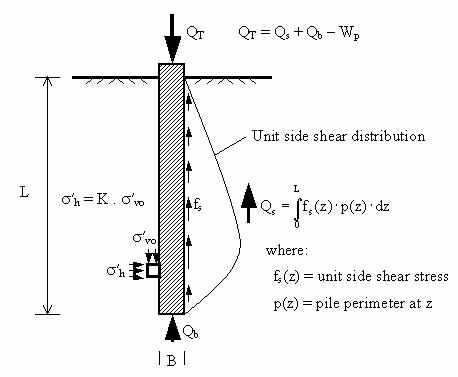
Figure 147. Illustration. Load transfer in an axially
loaded pile.
The load capacity contributed by the shaft side shear (Qs) is calculated by integrating the side shear stresses along the pile's embedded length:
where fs(z) is the shear stress between the pile and the soil at a depth z, p(z) is the pile perimeter at depth z, and L is the embedment depth of the pile.
The expression used for the tip or end-bearing of the pile is usually of the form:
where Ab is the tip or end area of the pile, and qb is the total ultimate end-bearing or tip stress.
The different pile capacity determination methods deal with ways of estimating the side friction (fs) and the ultimate end-bearing stress (qb). The following sections summarize the most common methods used in practice to estimate fs and qb for piles driven in sands.
Nordlund's method is often used by U.S. highway agencies and is advocated by the FHWA (Olson 2002). Nordlund's method is a semiempirical method based on a database of pile load tests (Nordlund 1963, 1979). The method accounts for differences in soil-pile interface for different piles. For the sake of brevity, only the most pertinent details of the method are presented. A complete description of this method can be found in Hannigan, et al. (1996).
According to the Nordlund's method, the shaft shear stress (fs) of a uniform cross section of pile embedded at a length L can be estimated as follows (Hannigan, et al., 1996):
where
Kd = coefficient of lateral earth pressure
CF = correction factor for
Kd when d ? ![]()
= free-field effective overburden pressure at depth z
d = interface friction angle between pile and soil
As pointed out by Olson (2002), the term ![]() 'v(z) in equation 19
should, rigorously speaking, correspond to the effective vertical
stress at depth z, right next to the pile shaft. Because this
stress is unknown, it is common to use the free-field vertical
stress that corresponds to the in situ value far away from the
influence of the pile.
'v(z) in equation 19
should, rigorously speaking, correspond to the effective vertical
stress at depth z, right next to the pile shaft. Because this
stress is unknown, it is common to use the free-field vertical
stress that corresponds to the in situ value far away from the
influence of the pile.
The expression proposed by Nordlund for the ultimate end-bearing stress (qb) is as follows:
where
![]() T = dimensionless
factor dependent on pile depth-width ratio
T = dimensionless
factor dependent on pile depth-width ratio
N'q = bearing capacity factor (function of
![]() ')
')
![]() ’v (z = L) =
free-field effective overburden pressure at the pile tip
(z = L)
’v (z = L) =
free-field effective overburden pressure at the pile tip
(z = L)
Values for the coefficients Kd,CF ,
N'q, and ![]() T, and
for the interface friction angle d, are typically read from design
charts found in the technical literature, such as the FHWA manual
for driven piles (Hannigan, et al., 1996).
T, and
for the interface friction angle d, are typically read from design
charts found in the technical literature, such as the FHWA manual
for driven piles (Hannigan, et al., 1996).
The American Petroleum Institute (API) provides design recommendations for axially loaded piles in the API RP 2A publication titled Recommended Practice for Planning, Designing, and Constructing Fixed Offshore Platforms (API 1993). Although this method is not as commonly used by highway agencies as is Nordlund's method, it is worth presenting here because the API recommendations are based on a large database of axial pile load tests that is continually evaluated and updated (Pelletier, et al., 1993).
According to API (1993), the shaft shear for piles in sands can be estimated using:
where
![]() 'v(z) =
free-field effective overburden pressure at depth z
'v(z) =
free-field effective overburden pressure at depth z
K = earth pressure coefficient
d = interface friction angle between pile and soil (as per table 36)
API (1993) recommends using a value of 1.0 for the earth pressure coefficient (K) for full displacement piles, such as the piles tested in this project. Equation 21 implies that the shaft friction can increase indefinitely with depth (i.e., with increasing effective overburden pressure). However, API recommends using limiting values for fs, as shown in table 36. In the absence of interface friction angle test data, API recommends using the values of soil-pile interface friction angles (d) listed in table 36.
|
Density |
Soil Description |
Soil-Pile Interface Friction Angle, d2 (degrees) |
Limiting Shaft Friction, fs |
|
|---|---|---|---|---|
|
(kips/ft2) |
(kPa) |
|||
|
Very loose |
Sand |
15 |
1.0 |
47.8 |
|
Loose |
Sand-silt 3 |
|||
|
Medium |
Silt |
|||
|
Loose |
Sand |
20 |
1.4 |
67.0 |
|
Medium |
Sand-silt |
|||
|
Dense |
Silt |
|||
|
Medium |
Sand |
25 |
1.7 |
81.3 |
|
Dense |
Sand-silt |
|||
|
Dense |
Sand |
30 |
2.0 |
95.7 |
|
Very dense |
Sand-silt |
|||
|
Dense |
Sand |
35 |
2.4 |
114.8 |
|
Very dense |
Sand-silt |
|||
Notes: (1) These values provided by API are intended as
guidelines only, and where detailed information is available other
values may be justified.
(2) Suggested values are for steel pipe piles driven in
cohesionless soils.
(3) Sand-silt is described as soils with significant fraction of
both sand and silt.
API recommends using the following expression to estimate the ultimate end-bearing or tip resistance for piles driven in sands:
where
s'v(z = L) = free-field effective overburden pressure at the pile tip (z = L)
Nq = bearing capacity factor (as per table 37)
Similarly to fs, API recommends limiting the value of the tip resistance (qb). The recommended values of Nq and limiting qb are shown in table 37.
|
Density |
Soil Description |
Nq |
Limiting Tip Resistance, qb |
|
|---|---|---|---|---|
|
(kips/ft2) |
(MPa) |
|||
|
Very loose |
Sand |
8 |
40 |
1.9 |
|
Loose |
Sand-silt |
|||
|
Medium |
Silt |
|||
|
Loose |
Sand |
12 |
60 |
2.9 |
|
Medium |
Sand-silt |
|||
|
Dense |
Silt |
|||
|
Medium |
Sand |
20 |
100 |
4.8 |
|
Dense |
Sand-silt |
|||
|
Dense |
Sand |
40 |
200 |
9.6 |
|
Very dense |
Sand-silt |
|||
|
Dense |
Sand |
50 |
250 |
12.0 |
|
Very dense |
Sand-silt |
|||
The Laboratoire Central des Ponts et Chaussees (LCPC) method estimates pile capacities based on CPT tip resistance (qc) values (Bustamante and Gianeselli 1982). A detailed description of the method can be found in Lunne, et al., 1997.
The unit shaft resistance (fs) is determined based on the pile type, installation method, and the value of the CPT tip resistance (qc). The recommended pile shaft resistance is obtained by dividing the measured qc by a friction coefficient (aLCPC). A limiting shaft friction is recommended based on pile and soil type. The values of recommended friction coefficients, aLCPC, and maximum limit of fs for driven piles in sands are summarized in table 38.
|
State of Sand |
qc (MPa) |
Pile Category |
|||
|---|---|---|---|---|---|
|
Coefficient, aLCPC |
Maximum Limit of fs (MPa) |
||||
|
Concrete |
Steel |
Concrete |
Steel |
||
|
Loose |
= 5 |
60 |
120 |
0.035 |
0.035 |
|
Medium dense |
5 to 12 |
100 |
200 |
0.08 |
0.08 |
|
Dense to very dense |
> 12 |
150 |
200 |
0.12 |
0.12 |
1 MPa = 145 lbf/inch2
The LCPC method correlates the pile unit tip resistance (qb) to an equivalent average cone resistance (qca) calculated using the qc values within 1.5 pile diameters (or widths) below and above the pile tip elevation, as described by Lunne, et al. (1997). The LCPC pile tip resistance (qb) is calculated by multiplying the equivalent average cone resistance (qca) by an end bearing coefficient (kc). The recommended values for end-bearing factors for driven piles in sands are summarized in table 39.
|
State of Sand |
qc (MPa) |
Factor kc |
|---|---|---|
|
Loose |
= 5 |
0.5 |
|
Medium dense |
5 to 12 |
0.5 |
|
Dense to very dense |
> 12 |
0.4 |
1 MPa = 145 lbf/inch2
This method was developed at the Imperial College in London, England, by Jardine and his colleagues based on a series of investigations using instrumented field test piles (Jardine 1985, Bond 1989, Lehane 1992, Chow 1996). The instrumented piles were tubular closed and open-ended steel piles driven in sands for supporting offshore structures used in the oil industry.
The major findings of the Imperial College experiments, related to piles driven in sands, are summarized below (Jardine and Lehane 1993, Jardine and Chow 1996):
where
s'rf = the local radial effective stress at failure
df = dcv = failure or constant volume interface friction angle
where
s'rc(z) = local radial effective stress after installation
qc = CPT tip resistance
z = depth below ground surface
L = pile embedded length
h = L-z = distance to pile tip
s'v(z) = free-field effective overburden pressure at depth z
Pa = atmospheric pressure (= 100 kPa)
R = pile radius
h/R = 8 for points close to the tip where h < 8R
The Imperial College (IC) method provides a simple, practical, and rational approach to predict pile capacity of piles driven in sands. A complete description of the IC method can be found in Jardine and Chow (1996), and a brief description is presented here.
The basic steps involved in the IC method to estimate the shaft capacity of closed-ended driven piles in sands are:
where
G = operational shear modulus of sand (see note below)
dh = average radial displacement (see note below)
R = pile radius
Notes:
G: Since the shear stiffness of sands is nonlinear, pressure dependent, and anisotropic, the method recommends using reliable and appropriate measurements of the shear modulus. If these measurements are not available, the following expression (after Chow 1996) is recommended:
where
qc = CPT tip resistance
A = 0.0203
B = 0.00125
C = 1.216 x 10-6
s'v = free-field effective overburden pressure
Pa = atmospheric pressure (100 kPa)
dh: The term dh/R, in equation 25, comes from cylindrical cavity expansion theory, and corresponds to the cavity strain. The term dh refers to radial sand dilation, and can be estimated as being equal to the average peak-to-trough height obtained from surface roughness measurements of the pile (Chow 1996). The average peak-to-trough height (Ri) is equal to twice the centerline average roughness parameter (Rcla). Rcla is a surface roughness parameter commonly used by material scientists, and it is defined as the average distance of peaks and troughs to the surface profile centerline taken over an 8-mm (0.312-inch) gage length.
Calculate the local radial effective stress at failure, as follows:
where
s'rc from step 1 using equation 24
?s'rd from step 2 using equation 25
The IC method defines the tip resistance as the total utilizable tip resistance at a pile head displacement equal to 10 percent of the pile diameter. The recommended pile base resistance for closed-ended, driven piles in sand is related to the CPT tip resistance (qc,) averaged near the pile tip, according to the following empirical equation:
where
q bar subscript c = the CPT tip resistance averaged over 1.5 pile diameters above and below the pile tip
D = the pile diameter
DCPT = 0.036 m = the CPT diameter
The equation shown above is based on IC pile load test data that
showed that the measured profiles of pile tip resistance
(qb) fell close to the CPT qc traces. The
ratio qb/qc was found to be less than unity
and to decrease with pile diameter (Jardine and Chow 1996).
Equation 28 tends to zero at D = 3.6 m (11.8 ft); therefore, a
lower bound value of ![]() is recommended for D
> 2 m (6.56 ft).
is recommended for D
> 2 m (6.56 ft).
Predictions for the three piles tested at the Route 351 Bridge project were made using the four methods described in section 7.2.1. The predictions presented in the following sections were based on the geotechnical investigation results presented in chapter 6 and the interpreted average CPT and SPT design profiles, shown in figure 148. The predictions for each pile type included the specific information for each pile capacity prediction method. Pile-specific information included cross-sectional shape and dimensions, embedment depths, surface roughness, and interface friction values.
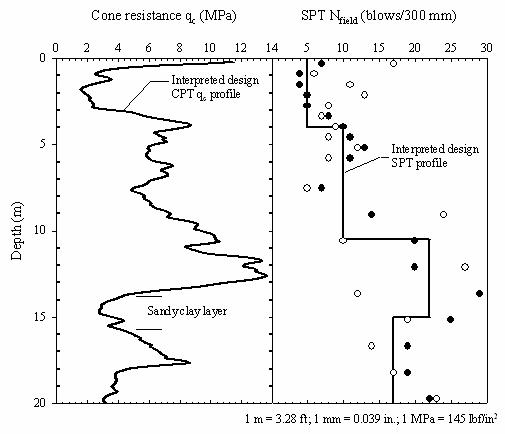
Figure 148. Graphs. Interpreted average CPT and SPT design
profiles for Route 351 test site.
Two sets of axial capacity predictions were made using Nordlund's method. One set of predictions was carried out using the recommended values of d read directly from the Nordlund's design charts. The curve for concrete was used for the prestressed concrete pile, and the curve for steel was used for the composite piles. The second set of Nordlund method predictions used the constant volume interface friction angles (dcv) obtained in this research, as presented in chapter 3. The two sets of axial pile capacity predictions using Nordlund's method were compared to the measured pile capacities evaluated from the load test results using the Davisson's failure criterion; these predictions are depicted in figures 149 and 150.
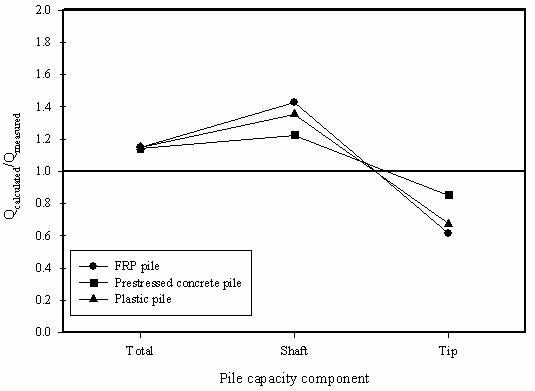
Figure 149. Graph. Accuracy of Nordlund's method
predictions using d values from Nordlund's charts.
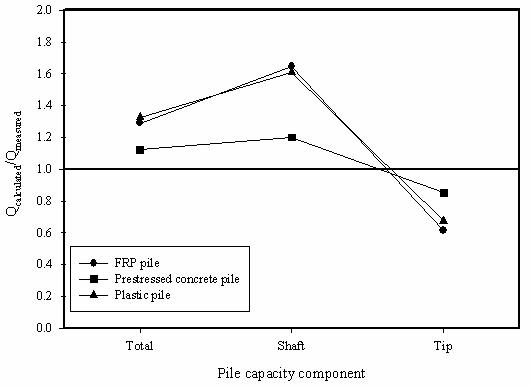
Figure 150. Graph. Accuracy of Nordlund's method
predictions using d values from interface shear tests.
Figures 149 and 150 show that the tip capacities (Qb) were underpredicted by about 35 percent for the composite piles and 15 percent for the prestressed concrete pile. The shaft capacities were overpredicted in both sets of predictions. The shaft capacities predicted using Nordlund's recommended interface friction angles, using the steel curve for the composite piles, were 35 to 43 percent higher than those measured for the composite piles and 23 percent higher for the prestressed concrete pile. The shaft capacities calculated using the d values from interface shear tests were about 65 percent higher for the composite piles and 20 percent higher for the prestressed concrete pile. The average coefficient of lateral earth pressure (Kd) from Nordlund's method was about 1.67. This value of Kd may be over predicting the effective radial normal stresses acting at the pile-soil interface, thereby producing higher shaft capacities than measured. To match the shaft capacities from the pile load tests, the coefficient of lateral earth pressure (Kd) would have to be around 1.0 for the composite piles and about 1.4 for the prestressed concrete pile, when using the d values from the interface shear tests.
Two sets of axial capacity predictions were made using the API (1993) method. One set of predictions was carried out using API's recommended value of d from table 36. The second set of API method predictions used the constant volume interface friction angles (dcv) from the interface shear tests presented in chapter 3. Comparisons of the two API predictions and the measured pile capacities are shown in figures 151 and 152.
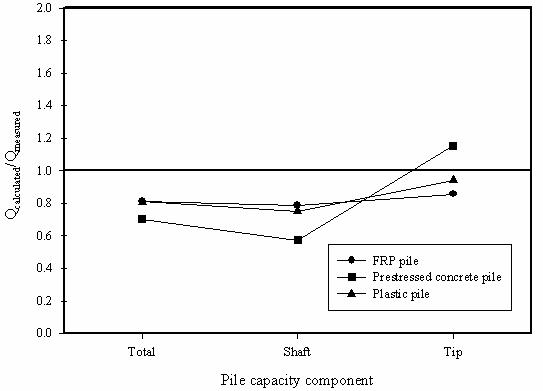
Figure 151. Graph. Accuracy of API method predictions using
d values from table 36.
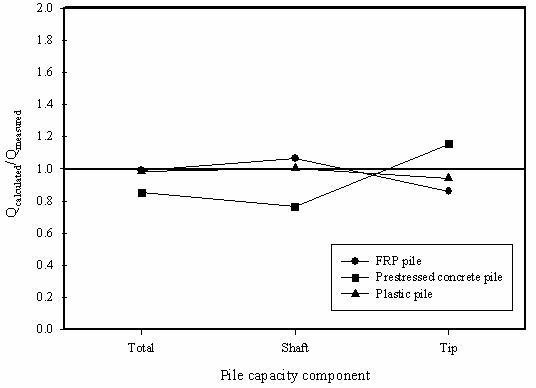
Figure 152. Graph. Accuracy of API method predictions using
d values from interface shear tests.
The tip capacities (Qb) predicted for the three piles, using the API method, were within ±15 percent of the measured values based on the Davisson failure criterion. The shaft capacities estimated using the API recommended interface friction angles, which are for steel pipe piles, were about 23 percent lower than measured for the composite piles and 43 percent lower for the prestressed concrete pile. The shaft capacities estimated using the d values from the interface shear tests were between 0.3 and 6 percent higher for the composite piles and 23.5 percent lower for the prestressed concrete pile. The average coefficient of lateral earth pressure (K) from the API method is 1.0. This value of K, coupled with the d values from the interface shear tests, resulted in very reasonable predictions of the pile shaft capacities for the composite piles.
Axial capacity predictions using the LCPC method (Bustamante and Gianeselli 1982) were based on the average obtained from applying the method to the CPT tip resistance (qc) data available at the test site, except that probe CPT-2 was excluded because it produced anomalous data in the depth range of 3 to 8 m (9.84 to 26.2 ft). For each pile type, two LCPC capacity calculations were performed: one assumes the particular pile under consideration is a steel pile, and the other assumes the pile is a concrete pile. Comparisons of the measured pile capacities and the LCPC predictions using the steel and concrete pile assumptions are shown in figures 153 and 154, respectively.
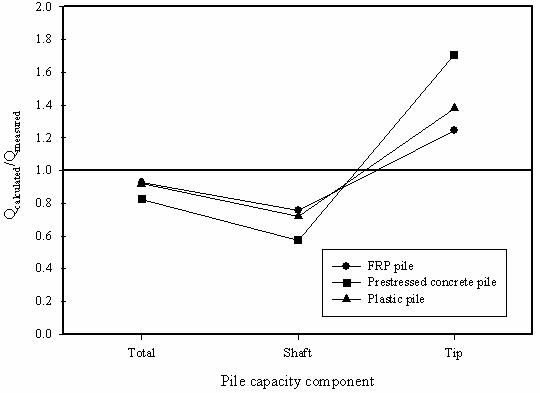
Figure 153. Graph. Accuracy of LCPC method predictions
using steel pile assumption.
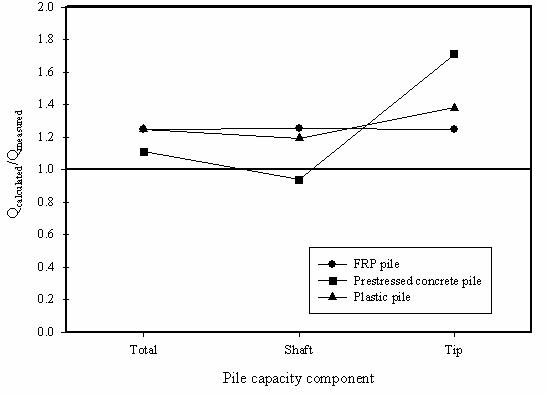
Figure 154. Graph. Accuracy of LCPC method predictions
using concrete pile assumption.
The tip capacities (Qb) estimated using the LCPC method over predicted the test results by 25 and 38 percent for the composite piles and by 71 percent for the prestressed concrete pile. The shaft capacities estimated using the LCPC steel pile approach were 24 and 28 percent lower than those measured for the composite piles and 43 percent lower for the prestressed concrete pile. The shaft capacities estimated using LCPC concrete pile approach were 19 and 25 percent higher than those measured for the composite piles and 6 percent lower for the prestressed concrete pile.
The IC method (Jardine and Chow 1996) was used to predict the axial capacities of the three test piles using the average interpreted design CPT tip resistance (qc) profile shown in figure 148, and the interface friction angle and surface roughness data presented in chapter 3. Comparisons of the measured pile capacities and the IC method predictions are shown in figure 155.
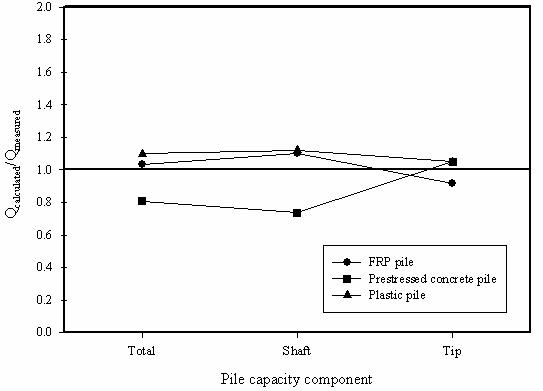
Figure 155. Graph. Accuracy of IC method predictions using
d values from interface shear tests.
The predicted tip capacities (Qb) using the IC method were 8 percent below those measured for the FRP composite pile, 5 percent above those measured for the plastic composite pile, and 5 percent above those measured for the prestressed concrete pile. The shaft capacities estimated using the IC approach were 10 and 12 percent higher than those measured for the composite piles, and 26 percent lower for the prestressed concrete pile. The level of agreement between measured and calculated capacities is quite good for all cases except the total and shaft capacities of the prestressed concrete pile.
The predicted axial pile capacities presented in the preceding sections are summarized in table 40.
|
Pile |
Prediction Method |
Total Capacity |
Shaft Capacity |
Toe Capacity |
|||
|---|---|---|---|---|---|---|---|
|
Qc (kN) |
Qc/Qm |
Qc (kN) |
Qc/Qm |
Qc (kN) |
Qc/Qm |
||
|
PSC |
Nordlund (w/ IST d's) |
3,480 |
1.12 |
2,890 |
1.2 |
590 |
0.85 |
|
Nordlund (Concrete) |
3,530 |
1.14 |
2,950 |
1.23 |
590 |
0.85 |
|
|
API (w/ recommended d's) |
2,180 |
0.7 |
1,380 |
0.57 |
800 |
1.16 |
|
|
API (w/ IST d's) |
2,640 |
0.85 |
1,840 |
0.76 |
800 |
1.16 |
|
|
LCPC-Steel |
2,560 |
0.83 |
1,380 |
0.57 |
1180 |
1.71 |
|
|
LCPC-Concrete |
3,440 |
1.11 |
2,260 |
0.94 |
1180 |
1.71 |
|
|
Imperial College |
2,500 |
0.81 |
1,770 |
0.74 |
720 |
1.05 |
|
|
FRP |
Nordlund (w/ IST d's) |
2,920 |
1.29 |
2,440 |
1.65 |
480 |
0.62 |
|
Nordlund (Steel) |
2,600 |
1.15 |
2,120 |
1.43 |
480 |
0.62 |
|
|
API (w/ recommended d's) |
1,830 |
0.81 |
1,160 |
0.79 |
670 |
0.86 |
|
|
API (w/ IST d's) |
2,240 |
0.99 |
1,570 |
1.06 |
670 |
0.86 |
|
|
LCPC-Steel |
2,090 |
0.93 |
1,120 |
0.76 |
970 |
1.25 |
|
|
LCPC-Concrete |
2,820 |
1.25 |
1,850 |
1.25 |
970 |
1.25 |
|
|
Imperial College |
2,340 |
1.04 |
1,630 |
1.1 |
710 |
0.92 |
|
|
Plastic |
Nordlund (w/ IST d's) |
2,830 |
1.33 |
2,400 |
1.61 |
430 |
0.68 |
|
Nordlund (Steel) |
2,450 |
1.15 |
2,010 |
1.35 |
430 |
0.68 |
|
|
API (w/ recommended d's) |
1,720 |
0.81 |
1,120 |
0.75 |
610 |
0.94 |
|
|
API (w/ IST d's) |
2,100 |
0.99 |
1,490 |
1 |
610 |
0.94 |
|
|
LCPC-Steel |
1,960 |
0.92 |
1,070 |
0.72 |
890 |
1.38 |
|
|
LCPC-Concrete |
2,660 |
1.25 |
1,770 |
1.19 |
890 |
1.38 |
|
|
Imperial College |
2,340 |
1.1 |
1,670 |
1.12 |
670 |
1.05 |
|
Notes: IST d's refers to interface friction angles from interface shear tests. Qc = calculated value (shown with three significant digits), Qm = measured value corresponding to Davisson's failure criterion. Qc/Qm = the ratio of calculated to measured. Conversion factor: 1 kN = 225 lbf.
The various methods used to predict axial pile capacity led to ratios of calculated-to- measured pile capacities (Qc/Qm) ranging from 0.70 to 1.14 for the prestressed concrete pile, and from 0.81 to 1.33 for the composite piles. If only the predictions from the IC method and the API method using the d-values from the interface shear tests are considered, the Qc/Qm ratios ranged from 0.81 to 0.85 for the prestressed concrete pile and from 0.99 to 1.10 for the composite piles. In other words, these two methods underpredict the capacity of the prestressed concrete pile by about 20 percent, and overpredict the capacities for the composite piles by about 10 percent. In routine deep-foundation design practice, factors of safety as low as 1.5 are sometimes used, but typically they are 2.0 or higher. Even a lower bound factor of safety of 1.5 would ensure that the ultimate geotechnical capacity of the composite piles is not exceeded, but it may not be high enough to ensure acceptable deformations of the foundation system.
In summary, it can be seen from the prediction results that the level of accuracy of the predictions is comparable for all three types of piles. In terms of axial pile capacity predictions, the results presented in this chapter seem to indicate that conventional static analysis methods are applicable to composite piles. However, additional case histories would be needed to corroborate and extend this conclusion to other composite pile types and to different soil conditions.
The settlement of a single pile in soil under compressive axial loading is a function of several factors, such as:
Several methods are reported in the literature for computation of load-settlement behavior of a single pile under axial compression loading. The methods are typically divided in the following main categories:
A good overview of the different techniques available can be found in Poulos (1989). For this study we focus mainly on the load-transfer (T-Z) methodology, which is commonly used by FHWA and U.S. State transportation agencies. This methodology has recently become more accessible to U.S. highway agencies with the release of the FB-Pier program, which uses this technique for settlement calculations of single and pile groups (Hoit, et al., 2000). The development of this program was sponsored by FHWA and is distributed freely to U.S. transportation agencies. Other commonly used programs that employ the T-Z methodology to analyze settlement of axially loaded single piles include A-Pile (Ensoft 1998) and CAXPILE (Dawkins 1982).
A brief overview of the load-transfer T-Z methodology is provided in the following section.
The load-transfer (T-Z) method is probably the most widely used technique to study the problem of single axially loaded piles, and is particularly useful when the soil behavior is clearly nonlinear and/or when the soil surrounding the pile is stratified. This method involves modeling the pile as a series of elements supported by discrete nonlinear springs, which represent the resistance of the soil in skin friction (T-Z springs), and a nonlinear spring at the pile tip representing the end-bearing (Qb-Z) spring. The soil springs are nonlinear representations of the soil reaction, T (or Qb for the pile tip), versus displacement (Z) as shown schematically in figure 156. Assuming the T-Z and Qb-Z curves are available, the axial load-settlement response can be obtained with the aid of a computer program such as FB-Pier.
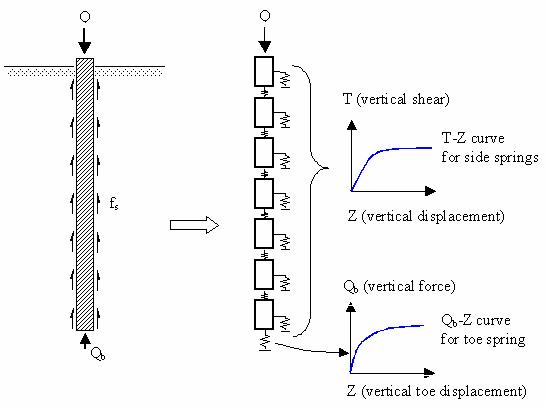
Figure 156. Illustration. Idealized model used in T-Z
load-transfer analyses.
Adequate T-Z and Qb-Z curves are essential in this method to obtain reliable settlement and load transfer calculations for axially loaded single piles. Such load-transfer curves were originally obtained empirically; one example is the work of Coyle and Sulaiman (1967), who published empirical T-Z curves based on model and full-scale pile load tests in sand. Building on this work, and based on additional empirical results, general recommendations for estimating T-Z and Qb-Z curves for driven piles in sands have been proposed by Vijayvergiya (1977) and API (1993). Load-transfer curves can also be constructed satisfactorily using a theoretical approach related to the shear stiffness of the soil surrounding the pile (Poulos 2001). Several methodologies to develop theoretically based load transfer curves have been proposed (e.g., Kraft, et al., 1981, Chow (1986), McVay, et al., 1989, and Randolph 1994).
Section 7.3.3 presents settlement predictions for the test piles using empirical load-transfer curves (API 1993, Vijayvergiya 1977), while section 7.3.4 presents prediction results using new theoretical load-transfer curves.
In the absence of more precise information, API (1993) recommends the use of the following T-Z curve expression for noncarbonate sands:
where
fs = the unit side shear stress mobilized along a pile segment at movement, z
fs, max = the maximum unit side shear stress
z = movement of pile segment
zc = movement required to mobilize fs, max (0.1 inches for sands)
In the absence of more definitive criteria, API (1993) recommends using the pile tip load versus tip settlement curve shown in figure 157.
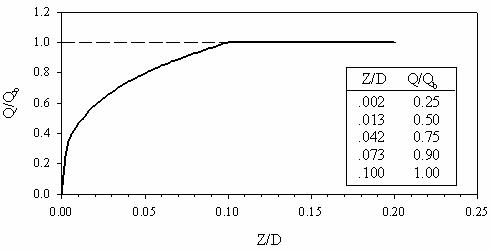
Figure 157. Graph. Pile tip load-pile tip displacement
curve (Q-Z) (API 1993).
In figure 157, Q is the mobilized end-bearing capacity at an axial tip displacement z, and Qb is the ultimate end-bearing load (computed using qb from equation 22 times the pile tip area). As shown in figure 157, Qb is mobilized at a pile tip displacement equal to 10 percent of the pile diameter, D.
As described previously in section 7.2.1.2, API recommends using maximum shear stresses for the pile shaft that increase linearly with depth until they reach a prescribed limiting value. Graphical representations of the maximum shaft shear stresses for the three test piles, as recommended by API (1993), are shown in figure 158. In section 7.2.3 it was indicated that better pile capacity estimates were obtained using the API method with d values from interface shear tests. Despite this finding, the shear stresses shown in figure 158 correspond to the d values recommended by API (1993). This was done to be able to assess the pile settlement predictions using the original method without major modifications.
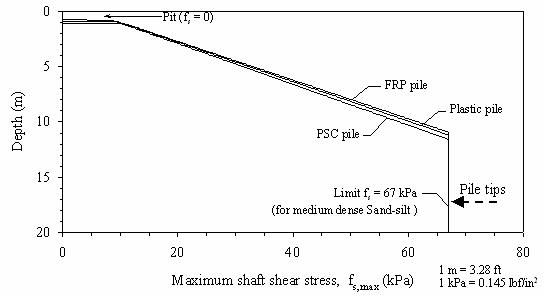
Figure
158. Graph. Maximum shear stress distribution along pile shaft,
according to API (1993).
The load-settlement responses predicted for the concrete test pile, using the API (1993) T-Z and Qb-Z curves, are shown in figure 159. The curve showing a lower predicted capacity is based on the API load-transfer curves using a limiting shear stress. The second prediction was made using the API curves but without a limiting shaft shear stress.
Figure 159 shows that the predicted settlement curves have relatively good agreement in the initial portion of the load settlement curve. However, they both underpredict the measured pile capacity. This is consistent with the axial pile capacity predictions presented in section 7.2.2.2, where the predicted API pile capacity (using the API recommended d values) was shown to be about 30 percent lower than measured. The predicted load-settlement curve using no limiting fs shows a slightly better agreement with the field measurements, but also underpredicts the pile capacity by about 18 percent. The extent of this underprediction is due to the low shaft capacity estimated using the API (1993) method, which (as indicated in section 7.2.2.2), was 43 percent lower than measured.
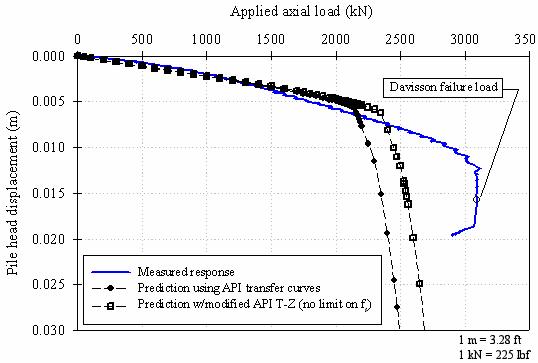
Figure 159. Graph. Settlement predictions for the
prestressed concrete pile using API (1993).
The predicted load-settlement curves for the FRP test pile, using the API (1993) load- transfer curves with and without a limiting shaft shear stress, are shown in figure 160.
Figure 160 shows a good agreement for the initial portions of the predicted settlement curves and the measured load-settlement curve. However, similar to the prestressed concrete pile predictions, the API prediction using an fs cutoff underpredicts the pile capacity, and the onset of large settlements occurs at lower load than observed in the field measurements. The prediction with no fs cutoff shows a much better correspondence with the field measurements, but also shows the onset of large settlements occurring at a load slightly below that measured in the field.
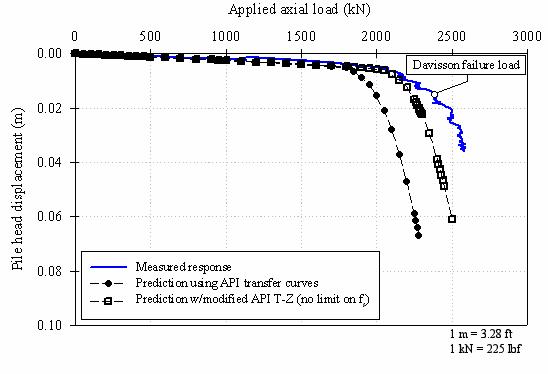
Figure 160. Graph. Settlement predictions for the FRP pile
using API (1993).
The predicted load-settlement curves for the plastic test pile, using the API (1993) load- transfer curves with and without a limiting shaft shear stress, are shown in figure 161.
Figure 161 shows that the predicted load-settlement curve, using the API (1993) method with a limiting fs, agrees well with the initial portion of the field measurements, but large settlements start to occur sooner than observed at about 1,700 kN (382,000 lbf). On the other hand, the API prediction using no fs cutoff shows very good agreement in both the initial and final portions of the settlement curve from the pile load test.
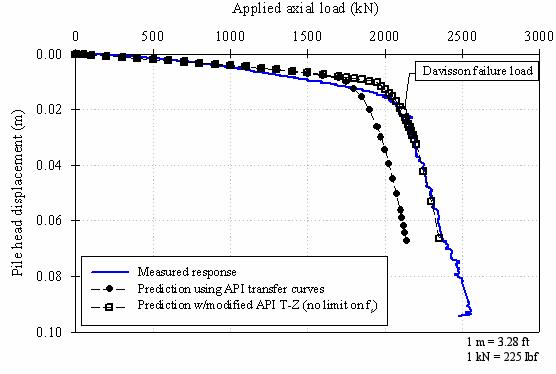
Figure 161. Graph. Settlement predictions for the plastic
pile using API (1993).
Vijayvergiya (1977) recommends the following load-transfer expression of mobilized unit side shear (fs) as a function of shaft movement (Z):
where
fs = the unit side shear stress mobilized along a pile segment at movement, z
fs, max = the maximum unit side shear stress
z = movement of pile segment
zc = movement required to mobilize fs, max (0.3 inches for sands)
The normalized T-Z curve obtained from equation 30 is shown in figure 162. For comparison purposes, the API (1993) T-Z curve is also shown in this figure.
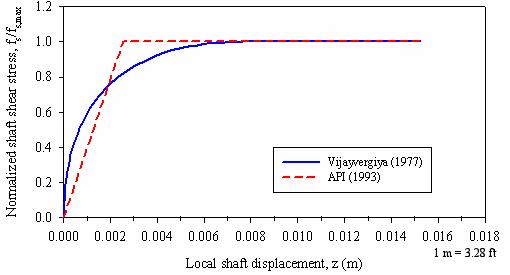
Figure 162. Graph. Normalized T-Z curves according to API
(1993) and Vijayvergiya (1977).
Similarly, the following expression for pile tip load versus tip settlement for piles in sands is proposed by Vijayvergiya (1977):
where
q = the pile tip resistance mobilized at displacement z
q max = the maximum tip resistance (end bearing)
z = movement of pile segment
zc = movement required to mobilize qmax (0.25 inch for sands)
The normalized Q-Z curve proposed by Vijayvergiya (1977) is shown in figure 163. For comparison purposes, the corresponding API (1993) curve for a 24-inch diameter pile is also shown.
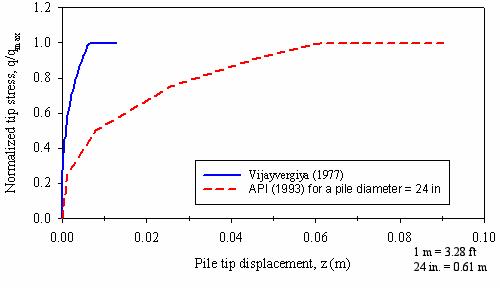
Figure 163. Graph. Normalized Q-Z curves according to
Vijayvergiya (1977) and API (1993).
It is clear from figure 163 that the Q-Z curve proposed by Vijayvergiya mobilizes the full end-bearing capacity at much smaller displacement than the API curve. Vijayvergiya (1977) estimates that about 6.35 mm (0.25 inches) of tip displacement are required to mobilize the ultimate pile end-bearing capacity, while API (1993) estimates that a pile tip displacement equal to 10 percent of the pile diameter is required.
Vijayvergiya (1977) recommended using an expression similar to API (1993) to estimate the maximum shear stresses along the pile (see equation 21). The author indicated that the coefficient of lateral earth pressures (K) can be as high as 1.25 for driven piles in medium-dense to dense sand.
The predictions presented in the following subsections are based on shaft shear stresses calculated using equation 21, with the d values from the interface shear tests presented in chapter 3, and K values of 1.0 and 1.25. The shear stress distributions used are shown in figure 164. No limiting value of shear stress was used, although it should be pointed out that Vijayvergiya (1977) does mention the existence of a limiting value in the 1971 version of the API guidelines.
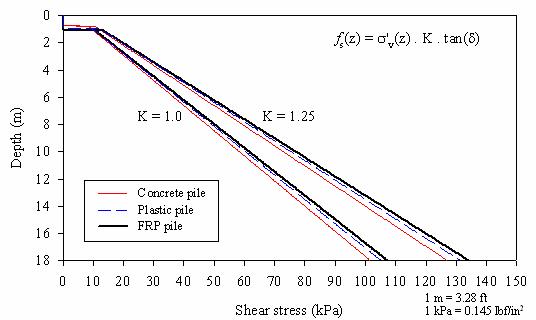
Figure 164. Graph. Maximum shear stress distributions used
in predictions using Vijayvergiya (1977).
Vijayvergiya (1977) recommends estimating the tip resistance for piles driven in sands as the product of a bearing capacity factor (Nq) and the free-field effective overburden stress at the base of the pile (s'v).
The values recommended by API (1993) were used in the predictions presented in the following sections.
The predicted load-settlement curves for the prestressed concrete test pile, using the recommendations proposed by Vijayvergiya (1977) for load-transfer curves, are shown in figure 165.
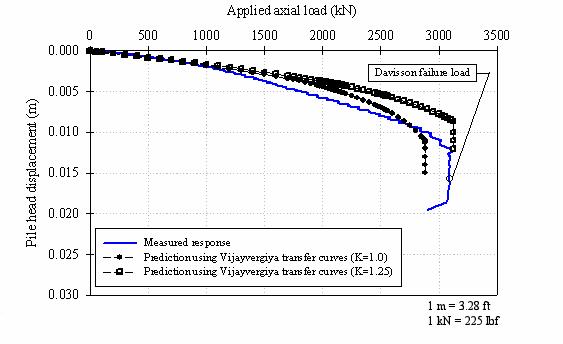
Figure 165. Graph. Settlement predictions for the concrete
pile using Vijayvergiya (1977).
Figure 165 shows that the predicted load-settlement curve, using Vijayvergiya's (1977) recommendations, agrees well with the initial portion of the field measurements, but shows a stiffer response for loads higher than 1,000 kN (225,000 lbf). The ultimate pile capacities, predicted using coefficients of lateral earth pressures (K) of 1.0 and 1.25, were about 2,885 and 3,125 kN (649,125 and 703,125 lbf), respectively. These capacities, as percentages of the pile capacity measured in the field, are about 93 percent and 101 percent for K equal to 1.0 and 1.25, respectively.
The predicted load-settlement curve for the FRP test pile, using the Vijayvergiya (1977) load-transfer curves with a coefficient of lateral earth pressure (K) equal to 1.0, is shown in figure 166.
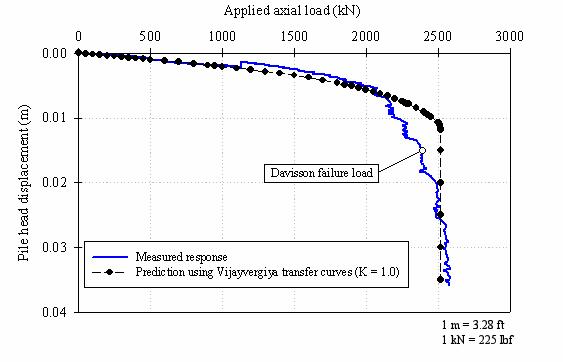
Figure 166. Graph. Settlement predictions for the FRP pile
using Vijayvergiya (1977).
Figure 166 shows that the predicted load-settlement curve, using Vijayvergiya's (1977) method with a lateral earth pressure coefficient (K) equal to 1.0, agrees reasonably well with the field measurements.
The predicted load-settlement curve for the FRP test pile, using the Vijayvergiya (1977) load transfer curves and with a lateral earth pressure coefficient (K) equal to 1.0, is shown in figure 167.
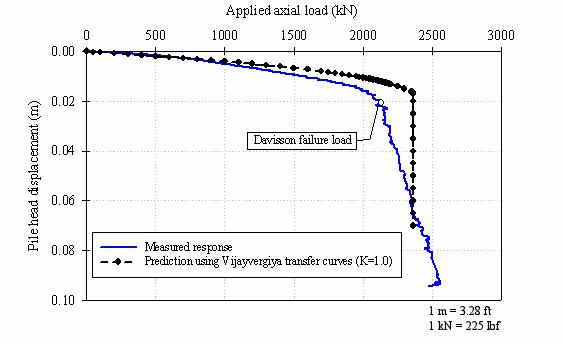
Figure 167. Graph. Settlement predictions for the plastic
pile using Vijayvergiya (1977).
Figure 167 shows that the predicted load-settlement curve, using Vijayvergiya's (1977) recommendations and with a lateral earth pressure coefficient (K) equal to 1.0, is stiffer than observed in the field.
The exactness of load-settlement behavior predicted using the load-transfer (T-Z) method depends to a great extent on the accuracy of the predicted ultimate shaft and tip capacities (e.g., as presented in section 7.2.2 for the API method), and on the displacement characteristics (e.g. stiffness, linear or nonlinear, displacement required for full-strength mobilization) chosen to model the soil-pile interface and the soil-pile tip during load transfer. For example, the results for the prestressed concrete pile, presented in the previous section and calculated using the API method, showed a significant underprediction of the pile capacity. This result is related to the low ultimate shaft resistance predicted compared to the actual ultimate shaft capacity recorded in the field. The prediction using Vijayvergiya's (1977) recommendations, with a coefficient of lateral earth pressure (K) equal to 1.25, was reasonably good. The predictions for the composite piles were more accurate because the calculated ultimate shaft and tip capacities were much closer to the actual values measured.
The following sections present the background and describe the methodology used in this research to develop theoretically based load-transfer curves. Most of the work in this area is based on the pioneering work by Kraft, et al. (1981).
The soil deformation around a pile shaft can be idealized as concentric cylinders in shear (Frank 1974, Randolph and Wroth 1978). This idealization assumes the soil displacement due to the pile loads is predominantly vertical, and that radial displacements are negligible. Studies by Frank (1974) and Baguelin, et al. (1975), have shown that the concentric cylinder approach is a good approximation of the deformation patterns obtained using more rigorous analyses such as the finite element method.
Randolph and Wroth (1978) derived an expression for pile settlement in a linear elastic soil based on the concentric cylinder assumption. The author's derivation starts by first considering the vertical equilibrium of the annular-shaped soil element (ring of soil between two concentric cylinders) shown in figure 168:
where the term definitions are shown in figure 168. The vertical stress (sy) shown in this figure refers to net change in vertical stress due to the axial load (P) applied to the pile.
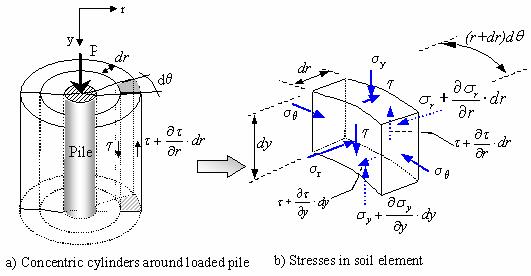
Figure 168. Illustrations. Concentric cylinder model for
settlement analysis of axially loaded piles (adapted from Randolph
and Wroth 1978).
Simplifying and neglecting second-order terms, equation 32 reduces to:
However, according to Randolph and Wroth (1978), the rate of change of vertical stress with respect to depth is much less than the rate of change of shear stress with respect to radial distance during axial loading of a pile. Therefore the second term of equation 33 can be neglected, and the equilibrium equation shown above can be approximated as:
Integrating this last expression, we obtain:
where
t(r) = shear stress acting at a radial distance (r) from the centerline of the pile
to = t(ro) = shear stress at the pile/soil interface (i.e., at a radial distance ro)
ro = pile radius (or equivalent radius for noncircular piles)
Equation 35 indicates that the shear stresses in the vicinity of the pile are inversely proportional to the radial distance to the pile.
The concentric cylinder model assumes that simple shear conditions prevail. This model also assumes that the radial displacements are negligible compared to the vertical displacements of the soil. Therefore the shear strain (?) can be approximated as:
where
u = radial displacement (neglected)
w = vertical displacement
For linear elastic soils, the shear strain is related to the shear stress as follows:
By substituting equation 35 into equation 37, we obtain:
The settlement of the pile shaft (ws) as originally proposed by Randolph and Wroth (1978), is obtained by integrating equation 38 and assuming a linear elastic soil with no radial variation of G (i.e., G(r) = G), as follows:
where rm is the radial distance at which shear stresses in the soil become negligible
Randolph and Wroth (1978) suggested estimating rm using the following empirical expression:
where
l = pile embedment depth
? = factor of vertical homogeneity of soil stiffness = G(at pile middepth)/G(at pile tip)
? = Poisson's ratio of the soil.
Equation 39 results in an equivalent linear T-Z load-transfer curve, as shown in figure 169. The stiffness or slope of this T-Z curve is:
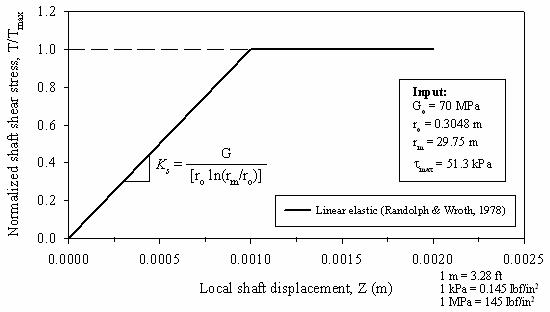
Figure 169. Graph. Linear T-Z curve obtained using Randolph
and Wroth (1978).
The value selected for rm has a large influence on the resulting pile settlement. A recent study by Guo and Randolph (1999) used finite element and fast Lagrangian analysis of continua (FLAC) analyses to determine the value of rm more precisely. As a first approximation, equation 40 provides reasonable values for rm (Randolph and Wroth 1978).
The load-transfer curve for the pile tip can be approximated using Boussinesq's solution for a rigid footing resting on an elastic half-space (Poulos and Davis 1990):
where
Qb = the pile tip load
Es, v = elastic modulus and Poisson's ratio of soil beneath pile tip
ro = pile radius
Equation 42 can be expressed in terms of the shear modulus by substituting
Es = 2G(1+?) as follows:
The resulting Qb-Z load transfer curve is shown in figure 170.
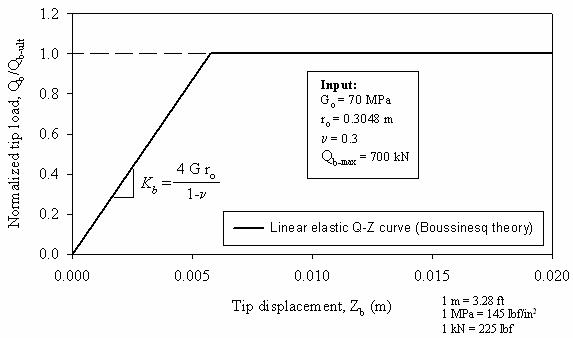
Figure 170. Graph. Linear Qb-Z curve obtained
using Boussinesq's theory.
The slope of the linear Qb-Z corresponds to the stiffness coefficient of the pile tip spring, and is given by:
In the preceding derivations it was assumed that the soil is linear and elastic, with the parameters G and v constant with both strain level and with radial distance from the pile. However, most soils exhibit stress-strain behavior that is highly nonlinear and their stiffness can decay rapidly with strains (Atkinson 2000). If settlement predictions are made using the linear elastic load-transfer curves shown above, the appropriate elastic properties should be used. Poulos (2001) recommends using a secant shear modulus corresponding to the load range applied to the pile. For the tip of a pile in sand, Poulos (2001) recommends increasing the shear modulus to account for soil densification below the pile tip due to driving. Successful application of a linear theory to a nonlinear problem requires judicious selection of elastic property values.
Nonlinear load-transfer curves that include soil nonlinearity are derived in the following subsections.
As shown in section 7.3.4.1, the shear stiffness of the soil deposit is a key property required in calculations of pile settlements. Sands typically only behave as linear elastic at very small shear strains of less than about 10 microstrains (? = 10-3 percent). The shear modulus in this range of very small shear strains is often referred to as the initial maximum or elastic shear modulus. Here it will be referred to as the initial shear modulus (Go). To perform nonlinear pile settlement analyses, the initial shear modulus profile along the length of the pile must be estimated.
Elastic theory relates Go to the shear wave speed (Vs) as follows:
where ? is the soil mass density
Therefore, the initial shear modulus could be obtained from in situ measurements of the shear wave speed, such as from seismic CPT soundings. If seismic tests are not available, as is the case for the Route 351 site, Go can be estimated using empirical correlations with in situ CPT tests (Lunne, et al., 1997).
Several equations have been proposed to estimate Go from CPT qc; some of the most important ones are:
where s’vo is the in situ effective overburden pressure at the depth of qc, and the units of Go, qc, ands’vo are in kPa.
where s’vo is the in situ effective overburden pressure at the depth of qc, and where Go, qc, and s’vo are in kPa.
where
qc = CPT tip resistance
A = 0.0203
B = 0.00125
C = 1.216 x 10-6
s'v = free-field effective overburden pressure
Pa = atmospheric pressure (100 kPa)
Hyperbolic stress-strain models have been found to adequately represent the nonlinear behavior of most soils (Kondner 1963, Kondner and Zelasko 1963, Duncan and Chang 1970). Use of hyperbolic functions to model nonlinear load-transfer functions for piles has been proposed by several researchers (e.g., Kraft, et al., 1981, Chow 1986, McVay, et al., 1989). The hyperbolic form of the shear stress-shear strain relationship is given by:
where
? = shear strain
Go = initial tangent shear modulus
tult = shear stress value that the hyperbola tends asymptotically (not to be confused with tmax)
t = shear stress value corresponding to strain, ?
Duncan and Chang (1970) related the asymptotic value, tult, to the maximum shear stress, tmax, by:
where Rf is the failure ratio, and is typically a value less than or equal to one; for values of Rf less than 1.0 the failure stress (tmax) is reached at a finite shear strain; for Rf equal to 1.0, the failure stress would be reached asymptotically at a shear strain of infinity.
By substituting equation 50 and t = Gsec? into equation 49, we obtain the following expression for the secant shear modulus:
If we include the radial variation of the shear stress (t) obtained earlier using the concentric cylinder assumption (i.e., by substituting equation 35 into equation 51), we obtain:
Substituting the secant modulus Gsec from equation 52 into equation 38, and evaluating the integral from radial distances ro to rm, we obtain the following nonlinear load-transfer (T-Z) relationship:
Equation 53 results in the T-Z load-transfer curve shown in figure 171. For comparison, the linear T-Z curve derived earlier is also shown. It can be seen that the initial stiffness or slope of the nonlinear T-Z curve is the same as the linear curve (equation 41). The equation shown above becomes the linear elastic T-Z curve of equation 39 when Rf = 0.
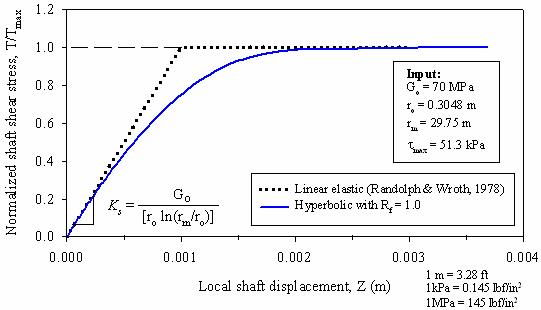
Figure 171. Graph. Hyperbolic T-Z curve.
For the hyperbolic model, the relationship between the normalized secant shear modulus (Gsec/Go) and the normalized shear stress (t/tmax) plots as a straight line with slope -Rf, as shown in figure 172 (as given from equation 51). Fahey and Carter (1993) and Fahey, et al. (1994), showed that the hyperbolic model appropriately represented the shear modulus degradation observed in cyclic test data, but found that for monotonic tests on both normally consolidated and overconsolidated sands, the shear modulus degraded at a much faster rate than suggested by the hyperbolic model. Randolph (1994) also pointed this out, and indicated that in practice, real soils often show a more rapid decay of the secant shear modulus with shear stress. This rapid reduction in Gsec is observed when the very low strain initial shear modulus, obtained from dynamic tests, is used as initial reference (Randolph 1994, Atkinson 2000). The value of the initial shear modulus measured using conventional laboratory tests is smaller than the "true" initial shear modulus at very small strains measured using dynamic measurements (Atkinson 2000). The stiffness measured using conventional laboratory tests is lower because it is affected by factors such as the quality of the soil sample, small disturbances during sample setup in the test apparatus, seating of loading platen, and small misalignments of loading ram (Atkinson 2000). The conventional hyperbolic model may be more appropriate to capture the soil nonlinearity when the initial modulus used is from conventional laboratory tests. However, for initial soil modulus based on dynamic test measurements, the modified hyperbolic model such as the one proposed by Fahey and Carter (1993) may be more suitable (Randolph 1994).
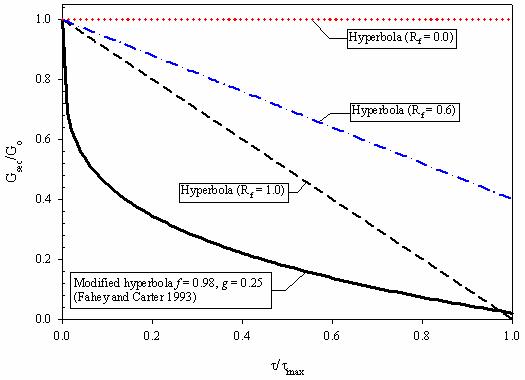
Figure 172. Graph. Variation of secant shear modulus for
different hyperbolic-type models.
To allow for a faster degradation of the secant shear modulus degradation, with respect to the "true" initial very low strain shear modulus, Fahey and Carter (1993) proposed using the following modified form of the hyperbolic expression:
where
Go = initial shear modulus (for shear strains below 10-5)
Gsec = secant shear modulus
t = current shear stress
tmax = maximum shear stress
f, g = empirical curve fitting parameters
Equation 54 becomes the standard hyperbolic model for f = Rf and g = 1. Fahey and Carter (1993) found that the values of f of 0.98 and g of 0.25 gave a good fit for normally consolidated Toyoura sand. Toyoura sand is the Japanese standard sand, and it consists of a subangular fine sand with a mean particle size (D50) of 0.17 mm (Ishihara 1996). This sand has characteristics similar to the in situ sand at the Route 351 project. The nonlinear T-Z curve, corresponding to the Fahey and Carter (1993) modified hyperbolic Gsec curve, can be easily derived using the same procedure as before. This expression is as follows:
Equation 55 becomes equation 53 (which corresponds to the conventional hyperbolic curve) when f = Rf and g = 1. The T-Z curve obtained using equation 55, and f = 0.98 and g = 0.25, is shown in figure 173. As shown in figure 173, the initial stiffness (Ks) of this T-Z curve is the same as the other two (since Ks depends only on Go, ro, and rm), but this curve degrades at a much faster rate than the one based on the conventional hyperbolic equation.
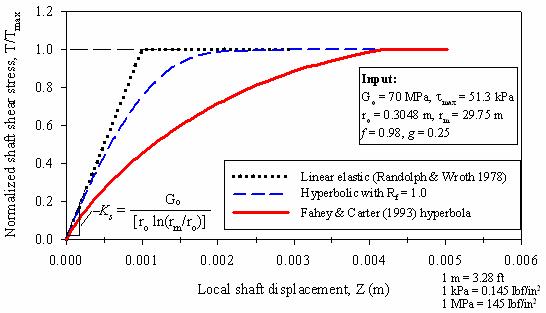
Figure 173. Graph. Theoretically derived T-Z curve using
concentric cylinders and the modified hyperbola from Fahey and
Carter (1993).
So far we have only dealt with the side shear load-transfer curves (T-Z curves). Because the nature of the shear strain distribution below a pile tip is more complex, it is not as straightforward to model soil nonlinearity for Q-Z curves as it was for the T-Z curves. An initial approximation consists of assuming a hyperbolic variation of the stiffness coefficient of the pile tip spring such as proposed by Chow (1986):
where Kobase is equal to Kbase from equation 44 (linear elastic soil case)
The expression for the load-transfer curve is:
The Qb-Z load-transfer curve obtained using equation 57 is shown in figure 174. For comparison purposes the linear elastic and conventional hyperbola curves are also shown.
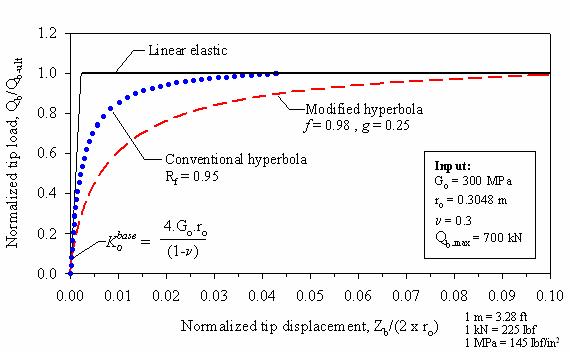
Figure 174. Graph. Theoretically derived Q-Z curve using
Boussinesq's theory and the modified hyperbola from Fahey and
Carter (1993).
As shown in figure 174, the ultimate tip resistance is developed at tip displacements of about 0.22 percent, 4.4 percent, and 10 percent, for the load-transfer curves based on the linear elastic, conventional hyperbolic (Rf = 0.95), and modified hyperbolic (f = 0.98, g = 0.25) models, respectively. The very small peak tip displacement in the linear elastic load-transfer curve is related to the use of the very low strain initial shear modulus. As mentioned earlier, use of a secant modulus is recommended to obtain more realistic displacements when using a linear elastic theory.
To analyze the piles tested at the Route 351 Bridge project site using the modified hyperbolic load-transfer curves derived above, adequate values for the initial shear modulus (for shaft and base), and the maximum loads for the load-transfer curves (i.e., the maximum shear stress for the shaft T-Z, and maximum end-bearing pressure for the pile tip Q-Z) must be selected. The following subsections describe this selection process in detail.
7.3.4.3.2 Initial shear modulus
The profiles of initial shear modulus obtained using the equations 26, 46, and 47 shown above, and the design CPT profile for the Route 351 test site (figure 148), are shown in figure 175.
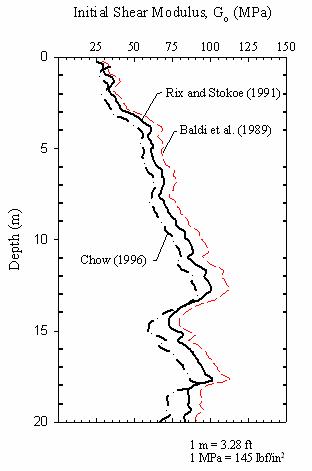
Figure 175. Graph. Route 351 initial shear modulus profile
from CPT correlations.
Both the magnitude and distribution (radially and with depth) are important. Poulos (2001) distinguished the following different values of the shear modulus required for settlement calculations of single piles:
Pile installation will greatly affect the shear modulus values in a zone near the pile (Poulos 1988). For driven piles in sands, the stiffness may actually be higher than the in situ value of the soil mass prior to pile installation (Randolph 1994). During pile installation the increase of radial stresses and associated densification will tend to increase the soil shear modulus; however, a competing effect which tends to reduce the shear modulus is the induced shear strains. The effects of pile installation on the magnitude and distribution of Go are difficult to quantify. If the installation effects are known, Kraft, et al. (1981), and Randolph (1994) have presented procedures that can be used to include the radial variation of shear modulus in the theoretical load-transfer curves. However, both considered the installation effects less important than the nonlinear effects and generally minor compared to the uncertainties involved in the estimated soil properties. Therefore, the analyses presented in the following sections are based on the Go profile presented in figure 175 with one exception: for the pile tip the Go value selected was based on an average of the in situ Go values measured immediately below the pile tip, multiplied by a factor of 4. This factor of 4 is used to account for sand densification below the pile tip. Poulos (2001) recommends increasing the in situ stiffness immediately below the tip of driven piles in sands by a factor between 3 and 5.
The maximum shear stresses are estimated using equation 21, using the interface friction angles obtained from interface friction tests. The coefficient of horizontal earth pressure (K) is assumed to range between 1.0 and 1.25. The range selected for K is consistent with the values recommended in the literature for displacement piles driven in sands (Bowles 1996, Poulos 2001).
The theoretical Qb-Z curves require as input, in addition to the initial shear modulus and the Poisson's ratio for the soil, the ultimate tip resistance, Qb-max. For the predictions presented in the following sections, the Qb-max values were selected from the Imperial College method estimates presented earlier (table 40). Qb-max values from other prediction methods could have been used, but the IC method had the closest toe capacity predictions.
The predicted load-settlement curves for the prestressed concrete test pile, using the proposed theoretically derived load-transfer curves, are shown in figure 176.
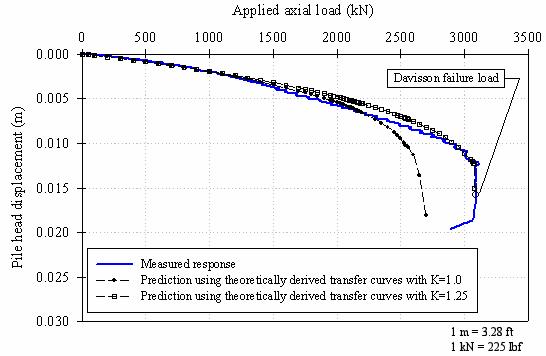
Figure 176. Graph. Settlement predictions for the concrete
pile using theoretically derived transfer curves.
Using the maximum shear stresses calculated with a coefficient of horizontal earth pressures (K) of 1.25, the predicted load curve is in reasonably good agreement with the measured response. The analysis with K = 1.25 predicts the initial slope of the load-settlement curve and ultimate pile capacity quite well, but shows a slightly stiffer response for loads between 1,500 and 2,900 kN (337,500 and 652,500 lbf).
Using the proposed theoretically derived load-transfer curves, and a value for K of 1.0, the load-settlement curve for the FRP test pile was predicted, as shown in figure 177.
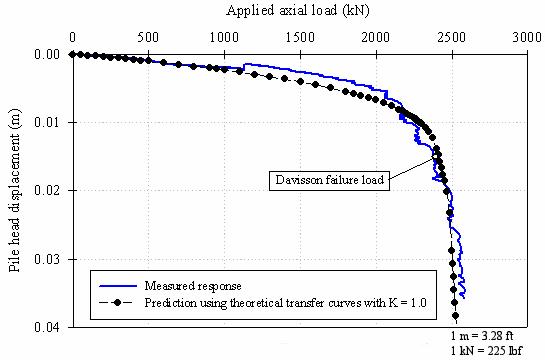
Figure 177. Graph. Settlement prediction for the FRP pile
using theoretically derived transfer curves.
Figure 177 shows a good agreement between the predicted load-settlement curve and the measured response.
The predicted load-settlement curves for the plastic test pile, using the proposed theoretically derived load-transfer curves, are shown in figure 178.
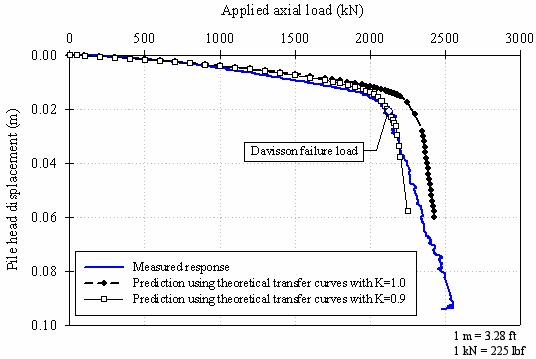
Figure
178. Graph. Settlement predictions for the plastic pile using
theoretically derived transfer curves.
Using the maximum shear stresses calculated with values of the coefficient of horizontal earth pressures (K) of 0.90 and 1.00, the predicted load curves are, up to an applied axial load of approximately 2,250 kN (506,250 lbf), in reasonably good agreement with the measured response. The analysis with K = 0.9 predicts well the load at which the steep change of slope occurs. However, neither of the analyses captures the slope of the second portion of the curve.
The predictions obtained using the theoretically derived load-transfer curves were in very good agreement with the measured field behavior. The best agreements were found for values of the coefficient of horizontal earth pressures (K) of 1.25, 1.0, and 0.9 for the prestressed concrete, FRP, and plastic piles, respectively. These differences in the K coefficient values are contrary to the expected outcome. The expected outcome was to have similar K values for the three test piles since they were installed in similar soil conditions, and all are full-displacement piles with similar cross sectional dimensions. It is possible that this result is again related to the d values measured in the laboratory not being representative of field conditions, perhaps due to the small displacements (only 0.5 inches (12.7 mm)) used in the lab.
The analyses presented in this chapter did not include the effects of residual stresses, although their importance in obtaining more accurate predictions is recognized. Based on the small level of residual stresses measured in the field (see chapter 6), the effects of residual stresses were not considered. The impact of not incorporating residual stress effects would likely affect stiffness in the pile response rather than ultimate capacity.
The axial capacities of the three test piles were predicted using static analysis methods commonly employed in practice. The methods employed were the Nordlund method, the API method, the LCPC method, and the IC method. The various methods used to predict axial pile capacity yielded ratios of calculated to measured pile capacities ranging from 0.70 to 1.14 for the prestressed concrete pile, and from 0.81 to 1.33 for the composite piles. It was found that the level of accuracy of the predictions was comparable for all three test piles.
The prediction results seem to indicate that conventional static analysis methods are applicable to composite piles. However, it is the author's opinion that additional case histories are needed to corroborate and extend this conclusion to other composite pile types and to different soil conditions.
The load-settlement behavior was predicted using T-Z analyses. Several of these analyses were carried out to determine the adequacy of this method to analyze axially loaded composite pile types such as those studied in this research project. The analyses were completed using empirical load-transfer curves available in the literature (e.g., API 1993, Vijayvergiya 1977) and theoretically derived load-transfer curves.
The predictions using the empirical load transfer curves showed reasonable agreement with the field measurements for the composite piles. The predictions for the prestressed concrete pile showed less agreement, and tended to underestimate the measured pile capacity. This result could be related to the value of the interface friction angle used. The calculations were based on the interface friction angle measured in the lab, which may be inadequate to represent the field conditions experience by the pile (e.g., in the field the pile interface experienced much larger relative displacements compared to the 0.5 inches (12.7 mm) used in the laboratory).
The predictions obtained using the theoretically derived load-transfer curves were in very good agreement with the measured field behavior. However, the values of the coefficient of horizontal earth pressures (K) that resulted in the best matches with field behavior were 1.25, 1.0, and 0.9 for the prestressed concrete, FRP, and plastic piles, respectively. The differences in the K coefficient values are contrary to the expected outcome. The expected outcome was to have similar K values for the three test piles since they were installed in similar soil conditions, and all are full-displacement piles with similar cross sectional dimensions. It is possible that this result is again related to the d values measured in the laboratory not being representative of field conditions, perhaps due to the small displacements (only 0.5 inches (12.7 mm)) used in the lab.
The prediction results seem to indicate that conventional T-Z analyses are applicable to composite piles. However, it is believed that additional case histories are needed to corroborate and extend this conclusion to other composite pile types and to different soil conditions.