U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| TECHBRIEF |
| This techbrief is an archived publication and may contain dated technical, contact, and link information |
| Publication Number: FHWA-HRT-14-063 Date: August 2014 |
Publication Number: FHWA-HRT-14-063 Date: August 2014 |
PDF files can be viewed with the Acrobat® Reader®
|
FHWA Publication No.: FHWA-HRT-14-063 FHWA Contact: Justin Ocel, HRDI-40, (202) 493-3080, justin.ocel@dot.gov This document is a technical summary of the published National Cooperative Highway Research Program Web-Only Document 197, Guidelines for the Load and Resistance Factor Design and Rating of Riveted, Bolted, and Welded Gusset-Plate Connections for Steel Bridges, available through the Transportation Research Board at http://www.trb.org/Main/Blurbs/168923.aspx. |
On August 1, 2007, the I-35W bridge collapsed in Minneapolis, MN. The bridge was a three-span (255 by 456 by 255 ft), continuous subdivided Warren deck truss over the Mississippi River. The National Transportation Safety Board (NTSB) investigated the collapse, with technical assistance from the Federal Highway Administration (FHWA). NTSB determined that the collapse was due to undersized gusset plates at a particular node location on the main truss. The plates should have been twice as thick or should have had twice the yield strength to provide adequate resistance to prevent the collapse.(1)
During the failure investigation, it was clear that the failure of I-35W was purely attributable to the gusset plate design. Recognizing that there could be lingering safety issues with other gusset plates in the bridge inventory, NTSB issued the following recommendation to FHWA on January 15, 2008:
"For all non-load-path-redundant steel truss bridges within the National Bridge Inventory, require that bridge owners conduct load capacity calculations to verify that the stress levels in all structural elements, including gusset plates, remain within applicable requirements whenever planned modifications or operational changes may significantly increase stresses." (1) |
On the same day, FHWA issued Technical Advisory (TA) 5140.29, which strongly encouraged bridge owners to check the capacity of gusset plates in their inventory.(2) At the time, bridge load ratings were member-centric and did not require connection elements to be rated, but the TA describes a paradigm shift in load rating. Based on feedback from many sources, it became apparent that there was no consensus on the specific procedures to follow for design or rating of gusset plates. At the time, the American Association of State Highway Transportation Officials (AASHTO) Bridge Design Specifications (BDS) were vague on the subject, leaving room for considerable engineering discretion and judgment in the process.(3) To provide a uniform standard for load rating gusset plates, FHWA issued a guidance document in February 2009, based on the best available information on gusset-plate behavior, outlining the minimum number of resistance equations that must be checked to adequately load rate a gusset plate.(4) For this TechBrief, this document will be referred to as the FHWA guide.
The FHWA guide provides rating guidance on both load and resistance factor rating (LRFR) and load factor rating philosophies. Discussions in this TechBrief are from the LRFR perspective only. The FHWA guide recommends five resistance checks at a minimum.
First, fasteners must be checked for adequate shear resistance for each connected member. In addition, the bearing resistance of the plate material must also be checked as part of the fastener checks. The FHWA guide refers to existing resistance checks in the load and resistance factor design (LRFD) BDS.(3) To assist with rating older riveted bridges, the FHWA guide also provides recommended shear strength values for rivets based on their age because this information is not provided in recent AASHTO specifications.
Second, relevant planes through the gusset must be checked for shear yielding and shear fracture. The one caveat associated with the shear yielding limit state is a suggested multiplication of the resistance by a factor, Ω, which the engineer has discretion to choose as 1.00 or 0.74. The Ω factor was first introduced in 1985 by the authors of the AASHTO Guide Specifications for Strength Design of Truss Bridges and accounts for assumptions in the shear stress distribution.(5) The specification writers recognized two potential outcomes: (1) the gusset plate would behave as a beam in bending along a shear plane, resulting in a parabolic distribution of stress (Ω═0.74), or (2) if adequately stiff or braced, the gusset plate would redistribute yielding along a shear plane until the entire section was mobilized (Ω═1.00). The original authors believed that gusset plate behavior could fall anywhere within these two bounds. Therefore, the FHWA guide left the selection of the factor to the discretion of the load-rating engineer. Finally, the Φ-factors for tension limit-states were applied to the shear limit-state checks, these being 0.95 for shear yielding and 0.80 for shear fracture. These values were set knowing that, for ductile materials, shear failures are technically tensile failures on inclined planes.
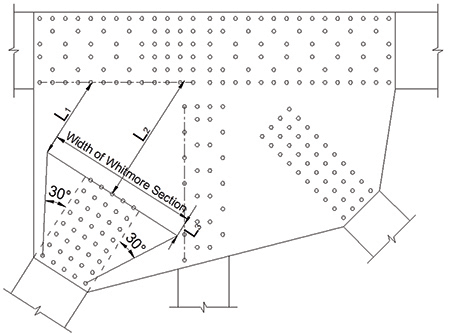
Third, the gusset plate must be checked for local stability around compression members. The buckling limit of the gusset plate is calculated by treating the zone of plate between the end of the compression member and adjoining members as an equivalent column and using the column formulas in the LRFD BDS to calculate capacity. This is done by defining an effective area over which the member axial load is assumed to be distributed. This area is referred to as the Whitmore section because it is based on the writings of Whitmore.(6) According to the Whitmore theory, the stress spreads out from the member into the gusset plate by dispersing at 30-degree angles from the first to the last row of fasteners. The width of the section is defined along the end row of fasteners and extending out to the dispersion lines. Finally, an equivalent column length is defined as the average of three lengths projected from the Whitmore section, in the direction of the member, to the fastener lines of the adjoining members. The three lengths are taken at the two ends of the width and at the center. If the Whitmore section intersects an adjoining member bolt line, the length at that end is assumed to be zero. This is schematically shown in figure 1. The load-rating engineer is given leeway to select an appropriate equivalent column length, or K-factor, depending on the likely buckling mode shape. Suggested ranges of K are given based on the rotational restraint at the ends and whether the gusset plate has lateral support to prevent sway.
Fourth, for tension members, the same Whitmore section is defined at the end of the tension members. On this section, both gross yielding and net section fracture must be checked. In addition, the fifth check is block shear resistance around tension members.
Early in the implementation of the FHWA guide, some gusset plates were not attaining desirable rating factors during load rating, leading States to retrofit or restrict loads on those bridges. Because many of these bridges had no long-standing history of performance problems, the common thought was the FHWA guide was overly conservative, particularly for fastener shear, gusset shear yielding, and Whitmore compression checks. AASHTO (through the National Academies), along with FHWA, sponsored an experimental program to further enhance the understanding of gusset plate failure mechanisms and create refined resistance equations that could predict the various failure modes of gusset plates. This project was the National Cooperative Highway Research Program (NCHRP) Project 12-84, Guidelines for the Load and Resistance Factor Design and Rating of Riveted, Bolted, and Welded Gusset-Plate Connections for Steel Bridges.(7)
The research included both experimental testing and analytical modeling. Primarily, the physical limitations and expense of experimental testing dictated that a small sampling of specimens would be tested to provide an adequate number of finite element model calibration points. Once robust modeling procedures were established, using the experimental results as a benchmark, a much broader study of different connection geometries could be investigated analytically to encompass the types of gusset plates that are in the Nation's inventory of truss bridges. The project goal was to collect the data to support, refute, or expand on the load rating checks in the FHWA guide. The data could then be adopted into the AASHTO BDS and Manual for Bridge Evaluation (MBE).(8,9)
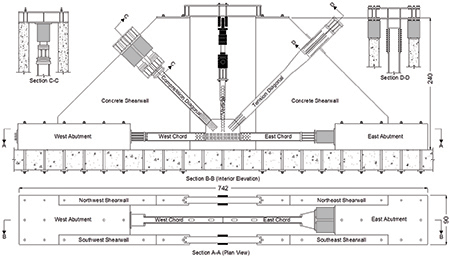
The experimental program specifically tested 12 full-scale gusset plate connections. The members were reusable, and each new specimen consisted of two new gusset plates and a set of chord splice plates. The configuration of the experimental connections used five separate members: two collinear chords, one compression diagonal framing at 45 degrees to the chord, one tension diagonal framing at 45 degrees to the chord, and a vertical member that could be in either tension or compression framing perpendicular to the chords. Figure 2 illustrates the special-purposed load frame constructed to test the gusset plate connections. Four of the five members had independent control of load via servovalve-controlled hydraulics. This setup offered the ability to investigate different equilibrium load combinations on the individual specimens.
The testing was conducted in two phases. The first phase established six unique geometries of plates. Different bolt strengths were investigated, along with the free edge length around the compression diagonal and span length of plate at the end of the compression diagonal. The plates tested had dimensions of roughly 60 inches wide by 36 inches tall. The phase 2 specimens used the same geometries but had modified plates with artificial section loss, edge stiffening, and multi-layered gussets.
Analytical models of the specimens helped define the level of detail needed to predict the experimental failure with accuracy. A three-dimensional shell model of the gusset plates and members was necessary to properly predict the failure of the connection. For the purposes of determining shear yielding and buckling, fastener holes did not need to be modeled. However, nonlinear material and geometric properties of the gusset plate were necessary, along with initial geometric imperfections.
The robust finite element modeling technique was applied to a parametric study that increased the breadth and depth of studied connection geometries over the experimental study. In particular, this included connections with diagonals framing at angles other than 45 degrees; chords that were not collinear; corner joints; Warren and Pratt configurations; loading scenarios representing joints over a pier, at midspan, and near inflection points of trusses; gusset plates with edge stiffening; gusset plates with section loss; and multilayered gusset plates. In total, there were 201 different models. Owing to the fidelity of the models, only buckling, shear yielding, and chord splice failure modes could be identified. The models did not have the fidelity to capture net section type failures.
Because many bridge owners had begun to load-rate gussets according to the FHWA guide while the research was ongoing, the conclusions and recommendations focus on improving and expanding the methodology as already defined. The following sections highlight the important results identified in the research.
Shear
In total, there were 44 observed shear-yielding failures from the experiments and analytical models. On average, the real shear-yielding load was 2 percent higher than the predicted 0.58FyAs value used in the FHWA guide. This would imply, in a nominal (unfactored) sense, that Ω should be 1.00. However, to account for the scatter in the data, Ω was selected as 0.88 for reasons to be explained later.
Buckling
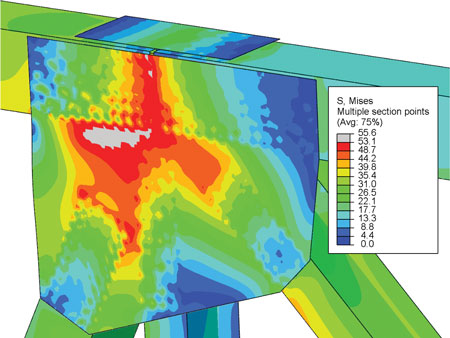
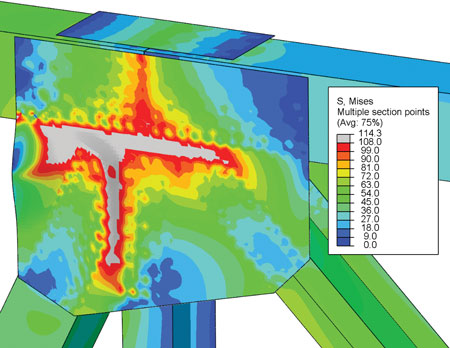
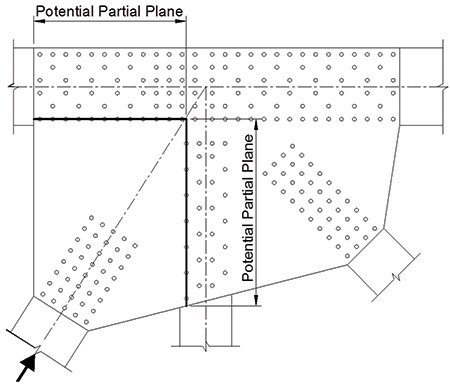
The analytical modeling matrix included the geometry at the ends of compression diagonals as a variable. In reviewing many truss plans, members often had chamfered ends so they could be spaced as close as possible to adjoining members. However, there was a substantial difference in buckling strength between chamfered compression members and those that were not. This contrast is highlighted in the stress contours in figure 3 and figure 4, which show similar connections with a non-chamfered and a chamfered diagonal, respectively. When the compression diagonal was not chamfered, buckling occurred with very little yielding, whereas when the chamfer was present, buckling still occurred, though after a significant amount of yielding. Closer analysis found that shear dominated the yielding along the chamfered edge. Hence, for joints with closely spaced members, the buckling strength was found to be coupled to the shear strength of the planes around the compression member. However, these shear planes are not across the full width or height of the plate and thus are referred to as partial shear planes. This led to a two-folded resistance check to determine buckling resistance. First, the Whitmore buckling resistance had to be evaluated, and the shear yielding on a partial plane around just the compression member also had to be checked. Figure 5 illustrates potential partial planes.
The FHWA guide check requires an effective column length based on the average of three lengths along the Whitmore width as described earlier. The work conducted throughout the research period found a better correlation when the effective column length was based only on the length at the middle of the Whitmore width, rather than the average of three lengths. In addition, a fixed K-factor of 0.5 was found applicable for all gusset plates in predicting the minimum buckling resistance.
In total, 124 experiments and analytical models were evaluated with the combined Whitmore buckling and partial plane shear yield checks to define the statistics to be used in the resistance factor calibration. In general, thin plates (⅜ inch thick or less) were controlled by the Whitmore buckling criteria, and thick plates were usually controlled by the partial plane shear yielding criteria.
Chord Splice
The FHWA guide suggests that Whitmore buckling and tension checks should be used to evaluate compression and tension chord splices.(4) In the analytical models that failed in the chord splice, the stress patterns did not match those of the assumed Whitmore section, in addition to the ambiguity of load sharing between the gusset plate and any splice plates. The research identified a resistance check that treated the gusset and splice plates as a single cross-section and considered the axial and bending component from the eccentric chord loads.
In total, 33 analytical models were observed to fail in the tension or compression chord splice. There were no experimental failures of chord splices.
Block Shear
This research specifically did not address the block shear limit state because there are abundant experimental data available in the open literature. The best summary of the available block shear data can be found in Huns, Grondin, and Driver. (10) This paper summarizes 133 experiments reported from 8 different sources. The paper provides the statistics needed for resistance factor calibration using the current AASHTO block shear equation. (8)
Other Tension Failure Modes
Only three analytical models had tension diagonal and/or vertical members that demonstrated pure tensile failure modes. All other models or specimens had tension members in conjunction with compression members that failed in buckling or shear. Therefore, there were no data available to provide a statistically significant sample to derive changes for tensile failure modes, so no changes were recommended to the FHWA guide for Whitmore tension checks.
Edge Stiffening
No correlation could be identified between the buckling resistance of a gusset plate and the free-edge slenderness of the plate itself. If properly detailed, edge stiffening could be used to increase the buckling resistance of a gusset plate, and this was proven both experimentally and analytically. In this case, properly detailed stiffeners would add out-of-plane stiffness to the compression member. Conventional edge stiffeners stiffen only the free edge and therefore offer no additional gains in buckling resistance. If stiffened properly, the Whitmore buckling criteria could be ignored, but the partial plane shear yielding resistance would still cap the overall resistance of the compression member.
No changes to the existing edge slenderness limit in the BDS were recommended because it represents good detailing practice to assist with transportation and erection. However, additional commentary was recommended to explain that it is not meant to suppress buckling. It was recommended not to rate gusset plates based on edge slenderness.
Corrosion
The effects of corrosion were investigated both experimentally and analytically, by applying localized areas of section loss. For shear limit states, it was found that resistance was based on the total cross sectional area in the plane of failure. Therefore, there was no effect from section loss being unbalanced across the gusset plate or unbalanced between the two plates.
Evaluation of buckling with section loss followed a similar reasoning. In this case, any section loss occurring between the Whitmore width and the adjoining member fastener lines is projected onto the Whitmore section, and an equivalent plate thickness is derived on the Whitmore section. This equivalent plate thickness is used in the resistance equations. Overall, this approach was found to be very conservative at times, but there were not enough failures to derive any better recommendation.
Multilayered gusset plates
For observed failures involving multilayered gusset plates, it was appropriate to add the individual resistances of each plate together to attain the overall resistance. However, consideration should be given to determining whether enough fasteners are being provided to develop the strength of each plate at the plane of failure.
The AASHTO Strength I and IV load combinations were used in the Monte Carlo analysis. Generically shown in figure 6 is the variation of the resistance factor, Φ, with the DL/LL ratio using the two AASHTO load combinations. The figure shows required resistance factor decreasing with the DL/LL for the Strength I load combination and increasing with DL/LL with Strength IV. Typically, the two would converge at a DL/LL between 6.0 and 8.0. The solid black line in the figure shows what the overall resistance factor should be between the two distributions. However, final resistance factors are defined at discrete DL/LL ratios for the Strength I load combination, rather than having a curve of many different ratios.
The results from this research made a distinction between design and rating, because the greater challenge is rating the existing inventory. It is more expensive to retrofit an existing gusset plate with an inadequate rating than to increase the plate thickness in design. It was out of scope for this project to define a target reliability for gusset plates. Therefore, a decision was made to base design resistance factors on the higher reliability index of 4.5, whereas AASHTO BDS uses a target reliability of 3.5. There were two reasons for this decision: 1) AASHTO already requires a higher level of reliability for fastener, weld, and block shear limit states, and 2) the American Institute of Steel Construction Steel Construction Manual uses two reliability indices (2.8 for member-centric limit states and 4.0 for connection-centric limit states).(12) Because gusset plates are a connection element, it seemed prudent to calibrate to a higher level of reliability.
The scatter in the resistance predictions was sensitive to the gusset plate thickness, so different calibrations were performed for the BDS and the MBE. The scatter associated with plates thinner than ⅜ inch was greater, leading to less favorable Φ-factors. Therefore, for design, it was assumed that a ⅜-inch thickness limit could be imposed for the gusset plates and that the data for "thin" gussets could be ignored. However, because the existing inventory of gusset plates has "thin" plates in it, the statistics used in determining MBE Φ-factors included all the data.
In design, the resistance factors were selected at a DL/LL ratio of 6.0 because this represents the most conservative value for Strength I because Strength IV will likely control at higher DL/LL ratios. This ratio would yield conservative resistance factors for more lightly loaded trusses. In addition, design resistance factors were calibrated at a target reliability index of 4.5. In rating, a different philosophy was adopted, primarily because of economics. (Using the design philosophy in rating would require posting of many trusses that have performed satisfactorily.) Resistance factors at a reliability index of 3.5 and at a DL/LL ratio of 1.0 were selected, but the use of system reliability factors for gusset plate rating was mandated. Long span trusses would unconservatively be rated because of the DL/LL effect, and an additional reduction factor was provided to account for the reduction in the resistance factor between DL/LL ratios of 1.0 and 6.0.
Table 1 shows the calibrated resistance factors that were recommended to AASHTO for the limit-states discussed in this TechBrief for both the BDS and MBE. The resistance factors are rounded to the nearest 0.05, in accordance with accepted practice. It should be noted that the calibrated resistance factors between full and partial plane shear yielding is the same. The Ω-factor was chosen as 0.88 because it resulted in resistance factors for both the BDS and MBE that were automatically rounded to the nearest 0.05. The chosen Ω-factor implies that gusset plates fully plastify (as described earlier in this TechBrief); this Ω-factor is an artifact of the calibration, and its continued use distinguishes between shear yielding of gusset plates and regular flexural members.
The resistance factors are different between the two specifications because the resistance factors were selected at different DL/LL ratios and reliability indices for the reasons explained above. In particular, the existing BDS resistance factor of 0.80 for block shear was found to have a reliability of 4.5. For rating, this resistance factor was increased to 1.00 to reflect the rating reliability index of 3.5.
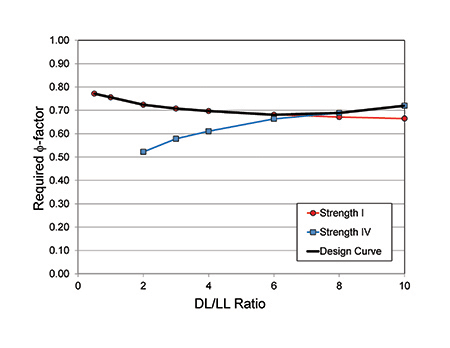
Table 1. Summary of resistance factors.
| Resistance Check | BDSa | MBEb |
|---|---|---|
Full and partial plane shear yielding |
0.80c |
1.00c |
Whitmore buckling (all data considered) |
— |
0.95 |
Whitmore buckling (neglecting plates thinner than 3/8 inch) |
0.75 |
— |
Block shear |
0.80 |
1.00 |
Chord splice (all data considered) |
— |
0.85 |
Chord splice (neglecting plates thinner than 3/8 inch) |
0.65 |
— |
|
—Not considered. |
There are two recommended areas for future work not addressed by this project. First, a live-load study of trusses should be performed to allow the use of less conservative live load statistics in the calibration. This study would have to consider a wide range of truss span lengths from approximately 40 to 800 ft.
Second, more work should be performed to refine the strength calculations of gusset plates around tension members. The three models that failed in the parametric study demonstrated coupled failures of an order beyond the simple Whitmore section check. The coupled mechanisms appeared to be the failure of the gusset on the boundary with the chord and vertical, which would be a combined tension and shear failure. The application of the block shear check did not predict failure well in these situations. In addition, the block shear check needs to be validated when failure planes can be merged between closely spaced tension members, creating a failure surface distorted from what is normally used in evaluating block shear.
National Transportation Safety Board, Collapse of I-35W Highway Bridge: Minneapolis, Minnesota, August 1, 2007, Highway Accident Report NTSB/HAR-08/03, Washington, DC, 2008.
U.S. Department of Transportation, Load-Carrying Capacity Considerations of Gusset Plates in Non-Load-Path-Redundant Steel Truss Bridges, Technical Advisory 5140.29, Federal Highway Administration, Washington, DC, 2008.
American Association of State Highway and Transportation Officials, AASHTO LRFD Bridge Design Specifications–4th Edition, Washington, DC, 2007.
Ibrahim, F.I.S., Load Rating Guidance and Examples for Bolted and Riveted Gusset Plates in Truss Bridges, FHWA-IF-09-014, Federal Highway Administration, Washington, DC, February 2009.
American Association of State Highway and Transportation Officials, Guide Specifications for Strength Design of Truss Bridges (Load Factor Design), Washington, DC, 1985.
Whitmore, R.E., Experimental Investigation of Stresses in Gusset Plates, Bulletin No. 16, Engineering Experiment Station, University of Tennessee, May 1952.
Transportation Research Board, Guidelines for the Load and Resistance Factor Design and Rating of Riveted, Bolted, and Welded Gusset-Plate Connections for Steel Bridges, NCHRP Project 12-84, National Cooperative Highway Research Program, Washington, DC, available at http://apps.trb.org/cmsfeed/TRBNetProjectDisplay.asp?ProjectID=2509.
American Association of State Highway and Transportation Officials, AASHTO LRFD Bridge Design Specifications–6th Edition, Washington, DC, 2012.
American Association of State Highway and Transportation Officials, The Manual for Bridge Evaluation–2nd Edition, Washington, DC, 2011.
Huns, B.S., Grondin, G.Y., and Driver, R.G., "Tension and Shear Block Failure of Bolted Gusset Plates," Canadian Journal of Civil Engineering, 33(4), pp. 395–408, April 2006.
Kulicki, J.M., Prucz, Z., Clancy, C.M., Mertz, D.R., and Nowak, A.S., Updating the Calibration Report for AASHTO LRFD Code, National Cooperative Highway Research Program Report 20-07/186, Transportation Research Board, Washington, DC, January 2007.
American Institute of Steel Construction, Steel Construction Manual—13th Edition, Chicago, IL, 2008.
|
Researchers—Justin Ocel of FHWA was the principal investigator for National Cooperative Research Program Project 12-84. The preceding principal investigators were Joey Hartmann and William Wright, both of FHWA during their tenure as principal investigator. The experimental work conducted at Turner-Fairbank was managed by Robert Zobel of Professional Service Industries, and digital images correlation data were collected and analyzed by Mark Iadicola of the National Institute of Standards and Technology. Georgia Institute of Technology was also a party to the research under the direction of Professors Don White and Roberto Leon, with work performed by Yoon Duk Kim, Yavuz Mentes, Towhid Bhuiyan, and Joon Wan Hu. Distribution—This TechBrief is being distributed according to a standard distribution. Direct distribution is being made to the Divisions and Resource Center. Availability—This TechBrief may be obtained from the FHWA Product Distribution Center by email to report.center@dot.gov, fax to (814) 239-2156, phone to (814) 239-1160, or online at https://www.fhwa.dot.gov/research. Key Words—Gusset plate, buckling, shear yielding, truss bridge, chord splice, Whitmore, bridge design, bridge rating, steel bridge. Notice—This document is disseminated under the sponsorship of the U.S. Department of Transportation in the interest of information exchange. The U.S. Government assumes no liability for the use of the information contained in this document. The U.S. Government does not endorse products or manufacturers. Trademarks or manufacturers' names appear in this report only because they are considered essential to the objective of the document. Quality Assurance Statement—The Federal Highway Administration (FHWA) provides high-quality information to serve the Government, industry, and public in a manner that promotes public understanding. Standards and policies are used to ensure and maximize the quality, objectivity, utility, and integrity of its information. FHWA periodically reviews quality issues and adjusts its programs and processes to ensure continuous quality improvement. |