This report is an archived publication and may contain dated technical, contact, and link information

Federal Highway Administration > Publications > Research Publications > 06139 > Appenda.Cfm Traffic Detector Handbook:Third Edition—Volume II

Publication Number: FHWA-HRT-06-139 Date: October 2006

Traffic Detector Handbook:Third Edition—Volume II

APPENDIX A. INDUCTIVE-LOOP SYSTEM EQUIVALENT CIRCUIT MODEL

ABSTRACT

The equivalent electrical circuit model for an inductive-loop system allows the loop’s inductance and quality factor to be calculated.

Appendix A describes the derivation and application of an equivalent circuit model and computer program that calculates the apparent self-inductance and quality factor versus frequency of square, rectangular, quadrupole, and circular loops of round wire buried in a roadway. The effects of transmission lines and matching transformers between the loop in the roadway and roadside electronics units are included in the model. The capacitance between the loop conductors and surrounding pavement material is shown to have a major effect on the magnitude of the loop’s apparent self-inductance.

Inductive-loop detectors are commonly used in actuated and computer–controlled traffic surveillance systems. The size, shape, and number of turns of wire in the loop should be designed to provide adequate vehicle detection sensitivity and prevent the lead-in wire and lead-in cable from reducing sensitivity. The inductance value at the input to the electronics unit must be within the range specified by the unit’s manufacturer. The computer program described in this appendix allows engineers to calculate the apparent loop inductance and quality factor versus operating frequency (20–60 kHz) for selected loop size, shape, wire diameter, number of turns, turn spacing, slot width, pavement loss tangent, and slot sealant dielectric constant.

INTRODUCTION

An inductive-loop detector system is composed of a buried loop of wire in the roadway pavement, which is connected with a transmission line (i.e., lead-in wire and lead-in cable) to a roadside electronics unit. When a vehicle is sensed by the loop, a small decrease in loop inductance is detected by the electronics unit. Furthermore, since the series inductance of the transmission line decreases the magnitude of the inductance change at the input to the electronics unit, the loop inductance should be larger than the transmission line series inductance. The loop inductance can be increased by winding additional turns into the loop and adding a transformer between the loop and transmission line.

The frequency range of typical electronics units is 20–60 kHz, although newer units that provide vehicle classification can operate at hundreds of kilohertz. Loop capacitance can cause the inductance sensed by the electronics unit to change significantly with frequency if too many turns are used in the roadway loop. To better predict inductive-loop system performance, an equivalent circuit model of the loop system was developed and programmed on a computer. The computer program allows inductiveloop system designers and maintenance technicians to calculate the detection system inductance and quality factor as a function of frequency, wire gauge size, wire spacing, etc.

The equivalent loop system model contains a roadway inductive-loop model, a transformer model, and a transmission line model. The calculation of the self-inductance of square, rectangular, and quadrupole loops is described elsewhere.^(1,2) King describes the calculation of the self-inductance of circular loops.⁽³⁾ This appendix expands the model to include the internal and external capacitance of such loops so that the high-frequency performance of the loop system can be calculated. A wideband transformer model is used. The transmission line model incorporates a complex characteristic impedance. All equations used in the loop computer program are included in this appendix.

LOOP CAPACITANCE THEORY

INTERNAL-LOOP CAPACITANCE

The stray capacitance between turns of wire in an inductive loop is calculated using a multilayer transformer model.

The capacitance between loop turns is calculated using a low-frequency, multilayer, transformer model.⁽⁴⁾ The model assumes uniform flux coupling through the loop turns with minimum leakage flux. Figure A-1 illustrates the capacitance between two adjacent isolated loop turns.

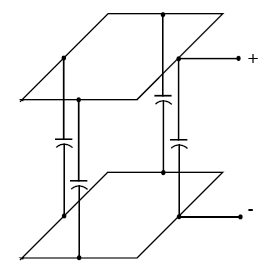
Figure A-1. Capacitance between adjacent isolated loop turns.

The loop wires are modeled as parallel transmission lines that have a capacitance per unit length C^' of ⁽⁵⁾

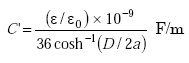(A-1)

where
	D	= spacing between conductor centers (m)
	a	= conductor radius (m)
	ε/ε0	= relative dielectric constant of the material that surrounds the turns of wire (equal to 1 for air)
	ε0	= permittivity of free space = 8.854 x 10–12 F/m.

The total capacitance between adjacent but isolated loop turns is given by

(A-2)

where P is the loop perimeter (m). A similar method was used by Palermo.⁽⁶⁾ The actual loop turns are connected as shown in figure A-2.

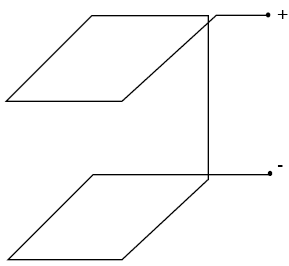
Figure A-2. Connection of adjacent loop turns.

The parallel transmission line is shorted at the end. The input capacitance of the shorted transmission line is given by

(A-3)

Figure A-3 shows the circuit model for a multiturn loop, where L_L represents the low-frequency inductance of the loop and C_Lⁱ the lumped internal capacitance across the loop terminals.

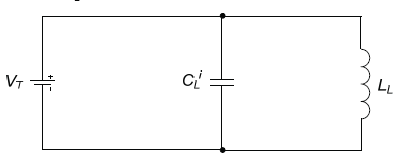
Figure A-3. Multiturn loop equivalent circuit model.

The total internal energy stored in the capacitor is

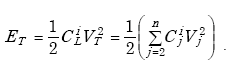(A-4)

When the voltage drop is linear, the voltage across each turn is directly proportional to the total voltage drop and inversely proportional to the number of turns. Accordingly,

(A-5)

and

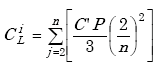(A-6)

where n is equal to the number of loop turns.

The lumped internal capacitance across the loop terminals is given by

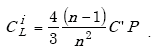(A-7)

This equation is identical to the equation for the capacitance between transformer winding layers with the exception of C^'.⁽⁷⁾

EXTERNAL-LOOP CAPACITANCE

External capacitance is created when a conductor is located in the vicinity of a dielectric material. This does not occur when a conductor is placed near another conducting surface such as a metal. Figure A-4 illustrates capacitive coupling between turns of loop wire (i.e., the conductor) and the edge boundaries of a sawcut or sealant (i.e., the dielectric). The dielectric constant of the material surrounding the wire is denoted by ε and its conductivity by σ. Since loop wires are typically closer to the top of the slot (i.e., sealant in the bottom of the slot supports the loop wire), the capacitive coupling between the wire and bottom of the slot was neglected.

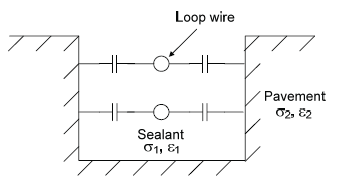
Figure A-4. Capacitance between loop conductors and slot.

Galejs determines the impedance of a buried insulated wire.⁽⁸⁾ The capacitance is calculated assuming the region surrounding the slot or cavity is finitely conducting. If region one is composed of low-loss dielectric, we can write⁽⁹⁾

(A-8)

Stratton also shows that a perfectly conducting outer conductor, as found in a coaxial line, provides a good approximation to a finitely conducting one when calculating shunt admittance.⁽¹⁰⁾ The slot walls are approximated by infinitely conducting ground planes, as illustrated in Figure A-5. These observations allow the combination of a coaxial conductor and TEM transmission line for use in modeling the capacitance of loop wires embedded in a slot.

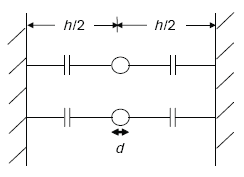
Figure A-5. Capacitance between loop conductors and infinitely conducting planes.

The characteristic impedance Z₀ of a coaxial conductor is given by⁽¹¹⁾

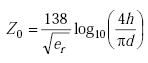(A-9)

where
	h	= sawcut slot width
	d	= diameter of loop wire.

The capacitance per unit length of a TEM transmission line is expressed as

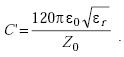(A-10)

Thus

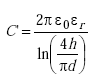(A-11)

or

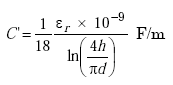(A-12)

where ln(x) = (2.303)[log₁₀(x)].

The total external capacitance for the loop conductor is

(A-13)

Inductive loops are typically balanced, as shown in Figure A-6.

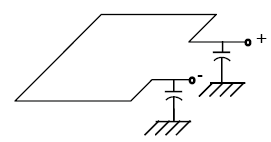
Figure A-6. Balanced inductive loop.

Because of the balanced configuration and zero potential point at the conductor perimeter center,

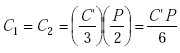(A-14)

Thus

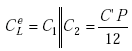(A-15)

where C₁||C₂ denotes the parallel connection of C₁ and C₂.

If only one side of the loop is grounded, then

(A-16)

LOOP RESISTANCE THEORY

LOOP RESISTANCE

The series loop resistance R_L is composed of the direct-current wire resistance R, the high-frequency skin-effect resistance R_ac, and the ground resistance R_g. The dominant resistance is the ground resistance, which is caused by currents induced in the conductive pavement and subgrade material. The ground resistance may limit loop sensitivity in locations with large moisture content. Ground resistance is calculated by assuming that the pavement and subgrade materials cause a magnetic loss similar to that of a ferrite or iron core in an inductor. The permeability µ_g of the pavement and subgrade material is assumed to be one. Appendix A-1, of this Appendix A, contains a derivation of the ground resistance.

The series loop resistance R_L is expressed as

(A-17)

where
	R	= direct-current loop resistance (Ω)
	Rac	= skin-effect resistance (Ω)
	Rg	= ground resistance (Ω)

(A-18)

	tanδg	= loss tangent of pavement material
	LL	= loop self-inductance (H)
	ω	= operating radian frequency = 2Πf (radians)
	f	= operating frequency (Hz).

INTERNAL INDUCTANCE AND RESISTANCE PER UNIT LENGTH FOR A CYLINDRICAL CONDUCTOR

Johnson shows that the ratio of actual internal inductance to low-frequency internal inductance and the ratio of internal resistance to low-frequency internal resistance are given by⁽¹²⁾

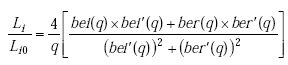(A-19)

and

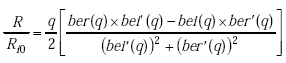(A-20)

Note: ber(q) is the real part of the complex Bessel function of the first kind. ber’(q) is the first derivative of the real part of the complex Bessel function of the first kind. bei(q) is the imaginary part of the complex Bessel function of the first kind. bei’(q) is first derivative of the imaginary part of the complex Bessel function of the first kind.

respectively, where

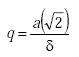(A-21)

	Li	= internal inductance (H/m)
	a	= radius of wire (m)
	δ	= skin depth (m),

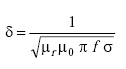(A-22)

	µ0	= permeability of free space = 4Π x 10–7 H/m
	µr	= relative permeability of copper wire = 1
	f	= operating frequency (Hz)
	σ	= conductivity of copper wire = 0.58 x 108 mhos/m
	Li0	= low-frequency internal inductance (H/m),

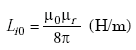(A-23)

		= 0.5 x 10-7 H/m for copper wire
	Ri0	= low-frequency internal resistance (Ω),

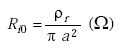(A-24)

	ρr	= resistivity (ohm-meter = Ωm)
		= 1.74 x 10–8 Ωm for copper wire.

LOOP-INDUCTANCE THEORY

SELF-INDUCTANCE OF SINGLE-TURN CIRCULAR LOOP

The self-inductance L₀ of a single-turn circular loop is given by⁽¹⁴⁾

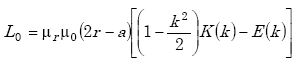(A-25)

where

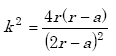(A-26)

	E(k)	= complete elliptic integral of first kind
	K(k)	= complete elliptic integral of second kind
	r	= radius of the loop coil relative to an axis normal to the plane of the loop that passes through the center of the loop (m)
	a	= radius of the loop wire (m).

Therefore, the radius from the axis to the inside edge of the loop wire is r – a. The formula for E(k) is found in Appendix A-3 of this Appendix A.⁽¹⁵⁾

SELF-INDUCTANCE OF MULTITURN CIRCULAR LOOP

Following King⁽¹⁷⁾, the inductance for a circular coil with N equally spaced identical turns is given by

(A-27)

or

(A-28)

where M_1,(i+1) is the mutual inductance between turn 1 and turn i+1. According to Ramo,⁽¹⁸⁾

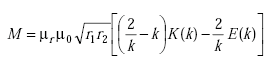(A-29)

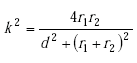(A-30)

where
	M	= mutual inductance (H)
	r1	= radius of turn one (m)
	r2	= radius of turn two (m)
	d	= spacing between turns (m).

EXTERNAL INDUCTANCE OF SINGLE-TURN RECTANGULAR LOOP

The external inductance of a single-turn rectangular loop is given by the sum of the inductance of two pairs of conductors. Thus

(A-31)

The external inductance of a single turn rectangular loop is⁽¹⁾

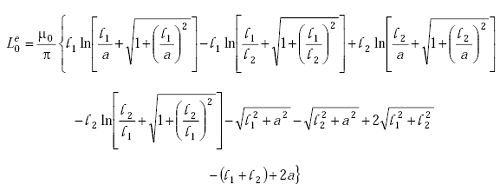(A-32)

where
	l1	= width of loop (m)
	l2	= length of loop (m)
	a	= radius of the conductor (m).

This equation can be written in more compact form by combining the logarithmic terms.

SELF-INDUCTANCE OF SINGLE-TURN RECTANGULAR LOOP

The self-inductance of a single-turn rectangular loop is given by the sum of internal and external inductances as

(A-33)

(A-34)

where Lⁱ is given by Equation A-19 and L^e₀ is given by Equation A-32.

SELF-INDUCTANCE OF MULTITURN RECTANGULAR LOOP

The self-inductance of a coil with N equally spaced identical turns is given by

(A-35)

MUTUAL INDUCTANCE OF PARALLEL FILAMENTARY CIRCUITS

The mutual inductance between a pair of filamentary circuits located in free space and illustrated in Figure A-7 is given by⁽¹⁹⁾

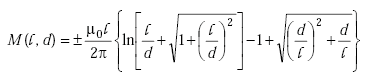(A-36)

where
	µ0	= permeability of free space = 4Π x 10–7 H/m
	l	= filamentary length (m)
	d	= filamentary spacing (m)
	M(l,d)	= mutual inductance (H).

The mutual inductance is positive when the current flow in the filaments is in the same direction and negative when the current flow is in opposite directions.

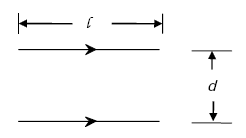
Figure A-7. Pair of parallel current elements.

MUTUAL INDUCTANCE OF TWO COAXIAL AND PARALLEL RECTANGULAR LOOPS

Equation A-36 can be used to calculate the total mutual inductance of the coaxial and parallel rectangular loops displayed in Figure A-8.

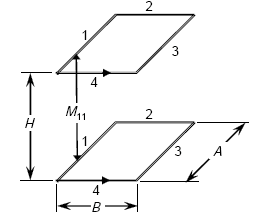
Figure A-8. Geometry for calculating mutual inductance of coaxial and parallel rectangular loops.

Accordingly, the total mutual inductance is given by the sum of the mutual inductances between the parallel sides as

(A-37)

where M₁₁ is the mutual inductance between side 1 of the bottom loop turn and side 1 of the top loop turn. All mutual inductances are symmetrical, e.g., M₁₃ = M₃₁ and M₂₄ = M₄₂.

SELF-INDUCTANCE OF MULTITURN QUADRUPOLE LOOP

Figure A-9 illustrates a two-turn quadrupole loop⁽²⁰⁾ and Figure A-10 a multiturn quadrupole loop.

The external inductance of an N-turn quadrupole loop is

(A-38)

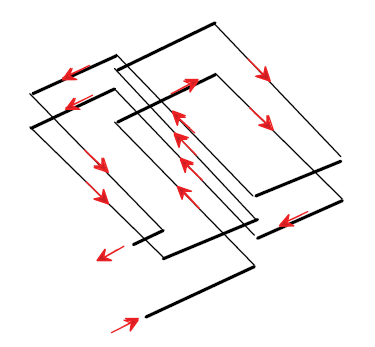
Figure A-9. Two-turn quadrupole loop.

Figure A-10. Multiturn quadrupole loop.

GENERAL FORMULA FOR MUTUAL INDUCTANCE OF PARALLEL FILAMENTS

In order to calculate the mutual inductance between the offset loops in the quadrupole loop model, a general formula for the mutual inductance of parallel, offset filaments is required. In Figure A-11, these filaments are labeled Segment i and Segment k.

Following Jefimenko⁽²¹⁾, the mutual inductance between the two parallel current filaments illustrated in Figure A-11 is given by

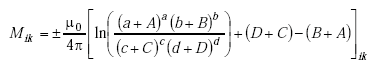(A-39)

where the positive sign is used for filaments with current flow in the same direction.

This expression assumes that the filament lengths are much less than the wavelength divided by 2p and the conductor radius is much less than the filament length. Grover⁽²²⁾ shows that this type of general formula can also be derived by applying the laws of summation of mutual inductance to Equation A-36.

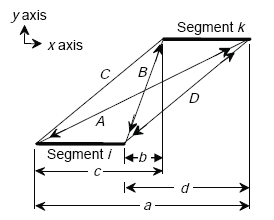
Figure A-11. Mutual inductance of two parallel segments i and k.

INDUCTIVE-LOOP CIRCUIT MODEL

Figure A-12 illustrates an inductive-loop system electrical circuit model that contains resistive, capacitive, and inductive components.

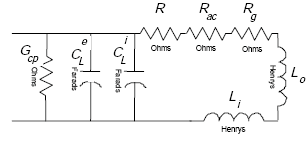
Figure A-12. Inductive-loop system circuit model.

Let

(A-40)

(A-41)

(A-42)

Following Johnson,⁽²³⁾ the slot dielectric loss conductance is

(A-43)

where tanδ_c is the loss tangent of the slot sealer material.

Appendix A-4, of this Appendix A, shows that the inductive-loop system circuit model of Figure A-12 reduces to the circuit model of Figure A-13,

where

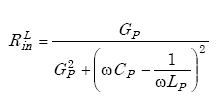(A-44)

and

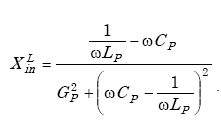(A-45)

The loop quality factor is given by

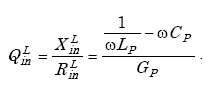(A-46)

The self-resonant frequency of the loop is given by

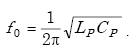(A-47)

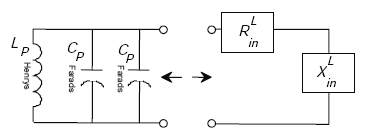
Figure A-13. Equivalent loop circuit model.

LOOP TRANSMISSION LINE THEORY

LOOP TRANSMISSION LINE MODEL

A transmission line connects the roadway loop with the roadside electronics unit. The complex impedance Z_L of the loop is transformed to a complex impedance Z_in by the transmission line cable according to⁽²⁴⁾

Note:The ratio of current to voltage is defined as conductance G = i / v. The unit of conductance is the mho (for inverse ohms) and is denoted by an inverted capital omega.

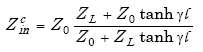(A-48)

where

(A-49)

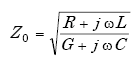(A-50)

(A-51)

and where
	R	= transmission line per unit resistance (Ω/m)
	G	= transmission line per unit conductance (mhos/m)
	L	= transmission line per unit inductance (H/m)
	C	= transmission line per unit capacitance (F/m)
	RL	= loop equivalent resistance (Ω)
	LL	= loop equivalent inductance (H)
	ω	= radian frequency (radians)
	l	= length of transmission line
	γ	= complex propagation constant.

A useful equation for computing Z_in is given by⁽²⁵⁾

(A-52)

FREQUENCY SHIFT ELECTRONICS UNIT SENSITIVITY

The frequency shift Δf_D at the terminals of the electronics unit is required to compute the sensitivity of the inductive-loop system as a function of loop and cable inductance.

Let

(A-53)

and

(A-54)

where f_V, f_NV are the frequencies measured by the electronics unit with and without a vehicle present.

The sensitivity S_D of the frequency shift electronics unit is defined as

(A-55)

The total inductance L_D at the electronics unit is the sum of the loop and cable inductances given by

(A-56)

Therefore, the change in inductance created by a vehicle passing over the loop is

(A-57)

since it is only the loop inductance that varies in the presence of a vehicle.

To convert the expression for sensitivity in terms of Δf_D/f_D to one in terms of ΔL_L/L_L, note that

(A-58)

Thus,

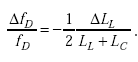(A-59)

By inspection,

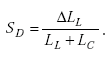(A-60)

Therefore,

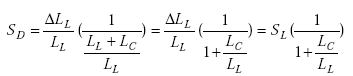(A-61)

and Equation A-55 becomes

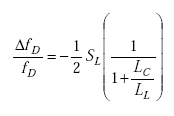(A-62)

where

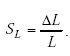(A-63)

Equation A-62 shows that the cable inductance L_C strongly affects the sensitivity of the frequency shift electronics unit. If the cable inductance is one-tenth or less of the loop inductance, the cable has a negligible effect on inductive-loop system sensitivity, provided the quality factor Q_D is five or greater. The frequency shift electronics unit sensitivity results also apply to period shift electronics units.

LOOP TRANSFORMER THEORY

INDUCTIVE-LOOP TRANSFORMER MODEL

A transformer with low leakage inductance (e.g., total series leakage inductance less than transmission line inductance) can be placed between the loop and transmission line to transform the loop inductance to a value larger than the transmission line inductance.⁽²⁶⁾ The transformer will remove the reduction in sensitivity caused by the transmission line.

The transformer model is shown in Figure A-14.⁽²⁷⁾

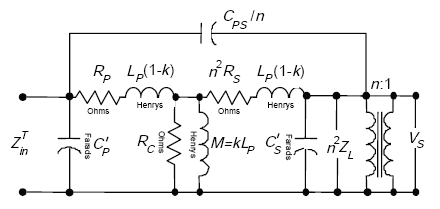
Figure A-14. Loop transformer model.

The definitions of the parameters that appear in Figure A-14 are referred to the primary of the transformer. Thus,

	RP	= primary winding resistance
	RC	= resistance corresponding to core loss
	n2RS	= referred secondary winding resistance
	n2ZL	= referred load impedance
	CP	= primary capacitance
	CS	= secondary capacitance
	CS'	= modified secondary shunting capacitance,

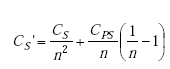(A-64)

	CPS/n	= referred primary to secondary capacitance
	CP'	= modified primary capacitance,

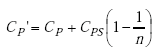(A-65)

n

= ratio of primary to secondary turns,

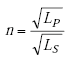(A-66)

	LP	= open circuit primary inductance at low frequency
	LP (1–K)	= one-half total leakage inductance
	K	= coupling coefficient,

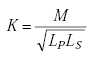(A-67)

M= mutual inductance.

The equivalent transformer model of Figure A-15 was used to derive an expression for the transformed load impedance Z_in^T.

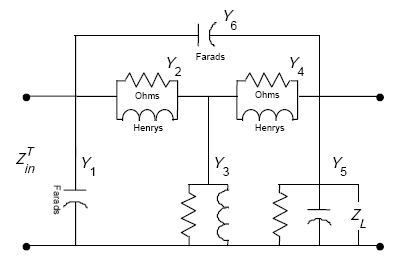
Figure A-15. Equivalent transformer model.

Appendix A-5, of this Appendix A, shows that the transformed load impedance is given by

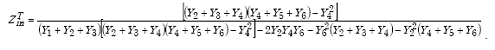(A-68)

LOOP-DETECTOR ANALYSIS SYSTEM PROGRAM

The loop-detector analysis system (LDAS) computer program calculates loop inductance and quality factor for rectangular, quadrupole, and circular loops. The loop inductance and quality factor are transformed by the transmission line (nonshielded, twisted-loop wire) to the roadside junction box and transmission line (shielded, twisted pair) between the junction box and electronics unit in the controller box. The program also models a transformer between the loop and transmission line or between the two types of transmission lines.

The LDAS program is menu driven and written in Microsoft QuickBasic. All mathematical functions are computed using double precision calculations.

COMPARISON OF CALCULATED AND MEASURED LOOP SELF-INDUCTANCE AND QUALITY FACTOR

Table A-1 contains measured self-inductance and quality factor data for a 6- x 6-ft (1.8- x 1.8-m) three-turn inductive loop. The measured and LDAS computed data compare favorably as shown in Table A-2. Measured loop inductance and quality factor data versus frequency were unavailable for quadrupole and circular loops.

Table A-1. Measured inductive-loop parameters of 3-turn 6- x 6-ft (1.8- x 1.8-m) loop with no vehicle present.

f0 (kH z )	f2 3dB (kHz)	f1 3dB(kHz)	Q=f0/f2-f1	C (µF)	L=1/(2πf0)2C (µH)	R=2Πf0L/Q (Ω)
20	20.334	19.702	31.7	0.856490	73.9	0.29
25	25.372	24.688	35.5	0.548109	73.9	0.33
30	30.388	29.644	40.3	0.380000	74.1	0.35
35	35.427	34.607	42.7	0.278693	74.2	0.38
40	40.470	39.573	44.6	0.212056	74.3	0.42
45	45.514	49.472	45.7	0.167887	74.5	0.46
50	50.571	49.472	45.5	0.135704	74.7	0.52
55	55.633	54.407	44.9	0.111845	74.9	0.58
60	60.704	59.342	44.1	0.093450	75.3	0.64

Loop size:	6 ft x 6 ft (1.83 m x 1.83 m)
Loop number of turns:	3
Loop wire size:	#14 AWG
Loop lead-in length:	60 in (1.5 m)
Loop self-resonant frequency:	697.06 kHz
50 pF residual capacitance in decade box neglected in C value

Table A-2. Comparison of measured and computed inductive-loop parameters of 3-turn 6- x 6-ft (1.8- x 1.8-m) loop with no vehicle present.

f0 (kHz)	Measured L (µH)	Calculated L (µH)	Measured Q	Calculated Q
20	73.9	74.4	31.7	30.4
25	73.9	74.4	35.5	33.9
30	74.1	74.3	40.3	36.6
35	74.2	74.3	42.7	38.8
40	74.3	74.3	44.6	40.6
45	74.5	74.3	45.7	42.2
50	74.7	74.3	45.5	43.7
55	74.9	74.3	44.9	44.9
60	75.3	74.3	44.1	46.1

Calculated loop parameters are based on:

Loop size: 6 ft x 6 ft (1.83 m x 1.83 m) Pavement loop slot width: 375 mils (0.95 cm) Loop slot sealant dielectric constant: 6 Pavement material loss tangent: 0.01 Loop wire insulation dielectric constant: 2.5 Effective loop wire insulation loss tangent: 0.001 Loop conductor spacing: 200 mils (0.51 cm) Wire gauge: #14 AWG

Tables A-3 through A-5 list calculated loop inductance and quality factor as a function of conductor size. The quality factor decreases with increasing wire gauge as expected. The addition of a transmission line of 240-ft (73.2-m) length approximately halves the quality factor. Inductive-loop detector applications requiring transmission lines over 200 ft (61 m) in length should use number #12 AWG wire for the loop and nonshielded transmission line. Three to four turns of loop wire have an adequate quality factor. One to two turn loops should be used with a transformer.

Table A-3. Rectangular-loop parameters.

Wire gauge (AWG)	1-Turn inductance µH)	1-Turn quality factor	2-Turn inductance(µH)	2-Turn quality factor	3-Turn inductance(µH)	3-Turn quality factor	4-Turn inductance(µH)	4-Turn quality factor	5-Turn inductance(µH)	5-Turn quality factor
12	10.13	19.68	35.22	29.88	73.28	37.13	123.14	42.65	184.00	47.03
14	10.50	15.61	35.96	24.06	74.39	30.40	124.62	35.41	185.85	39.51
14*	63.45	11.59	89.16	14.11	128.18	17.51	179.61	21.20	242.96	24.86
14**	351.70	1.77	853.20	4.90	1433.69	9.99	1985.51	17.24	2464.16	26.76
16	10.85	11.57	36.68	18.10	75.46	23.25	126.04	27.50	187.62	31.09
18	11.20	8.11	37.37	12.84	76.50	16.73	127.42	20.05	189.39	22.95

*  Transmission line
** Transformer loop
Notes:	20 kHz; loop size:6 ft x 6 ft (1.83 m x 1.83 m); other parameters are the same as those given for Table A-2. All inductance and quality factors in Table A-3 are apparent values (i.e., the effect of loop capacitance and resistance is included). Transformer parameters: Primary resistance (ohms) = 1 Primary capacitance (picofarads) = 10 Primary inductance (millihenrys) = 5 Secondary resistance (ohms) = 1 Secondary capacitance (picofarads) = 10 Primary to secondary turns ratio = 5 Core loss resistance (ohms) = 1,000,000 Coupling coefficient = 0.99 Primary to secondary capacitance (picofarads) = 10 Transmission line parameters Length = 240 ft (73.2 m) Resistance (milliohms/ft) = 2.5 (6.25 milliohms/m) Inductance (microhenrys/ft) = 0.22 (0,72 microhenrys/m) Conductance (microohms/ft) = 0.000076 (0.000249 microohms/m) Capacitance (picofarads/ft) = 26 (85.3 picofarads/m)

Table A-4. Quadrupole-loop parameters.

Wire gauge (AWG)	1-Turn inductance (µH)	1-Turn quality factor	2-Turn inductance (µH)	2-Turn quality factor	3-Turn inductance (µH)	3-Turn quality factor	4-Turn inductance (µH)	4-Turn quality factor	5-Turn inductance (µH)	5-Turn quality factor
12	17.14	21.72	60.15	32.74	125.42	40.32	210.78	45.93	314.77	50.27
14	17.69	17.26	61.26	26.53	127.08	33.28	212.98	38.48	317.49	42.64
16	18.22	12.81	62.32	20.07	128.67	25.67	215.09	30.18	320.10	33.91
18	18.74	8.99	63.36	14.32	130.22	18.61	217.15	22.21	322.65	25.29

Notes:

20 kHz; loop size:6 ft x 6 ft (1.83 m x 1.83 m); lateral conductor spacing: 200 mils (0.51 cm), other parameters are the same as those given for Table A-2. All inductance and quality factor values in Table A-4 are apparent values (i.e., the effect of loop capacitance and resistance is included).

Table A-5. Circular-loop parameters.

Wire gauge (AWG)	1-Turn inductance µH)	1-Turn quality factor	2-Turn inductance(µH)	2-Turn quality factor	3-Turn inductance(µH)	3-Turn quality factor	4-Turn inductance(µH)	4-Turn quality factor	5-Turn inductance(µH)	5-Turn quality factor
12	9.70	20.39	33.95	30.95	70.91	38.42	119.50	44.07	179.00	48.53
14	10.04	16.19	34.63	24.98	71.93	31.55	120.86	36.73	180.69	40.95
16	10.37	12.00	35.29	18.83	72.91	24.21	122.16	28.63	182.31	32.36
18	10.68	8.42	35.92	13.38	73.86	17.47	123.43	20.96	183.89	24.00

Notes:

20 kHz; loop diameter: 7 feet (2.1 m); other parameters are the same as those given for Table A-2. All inductance and quality factor values in Table A-5 are apparent values (i.e., the effect of loop capacitance and resistance is included).

CONCLUSIONS

Loop inductance should be measured at 1 kHz to remove effects of capacitance when determining the number of turns in a buried loop. All loop measurements at frequencies of 20 kHz or greater should be made with a balanced instrument since the loop electronics unit is balanced. An unbalanced measurement produces incorrect results because of the different capacitance-to-ground values. Since the external capacitance is determined by the dielectric constant of the slot sealing material, the loop wire should be completely sealed to prevent water from entering the loop slot. The large dielectric constant of water produces a significant change in the external capacitance and causes the apparent loop inductance to change. Thus, unstable loop operation can result from incomplete sealing of the loop sawcut.

APPENDIX A-1

LOOP GROUND-RESISTANCE DERIVATION

The complex impedance Z_L of the loop results from a complex permeability µ_g, where µ_g represents a complex number. The complex impedance is given by

(A-69)

(A-70)

The material loss tangent, denoted as tanδ_g, is given by

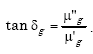(A-71)

Letting µ^'_g = 1, the loss tangent becomes

(A-72)

Then

(A-73)

(A-74)

When the complex impedance is written in the form

(A-75)

the real and imaginary parts of Z_L become

(A-76a)

and

(A-76b)

where R_g is the material ground loss and X_L is the inductive reactance.

APPENDIX A-2

REAL PART OF COMPLEX BESSEL FUNCTION OF FIRST KIND

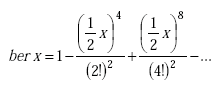(A-77)

or

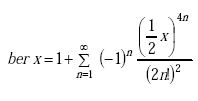(A-78)

DERIVATIVE OF REAL PART

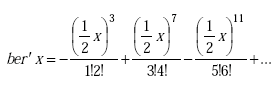(A-79)

or

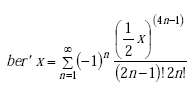(A-80)

IMAGINARY PART OF COMPLEX BESSEL FUNCTION OF FIRST KIND

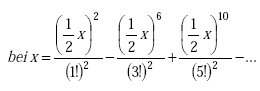(A-81)

or

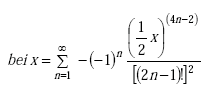(A-82)

DERIVATIVE OF IMAGINARY PART

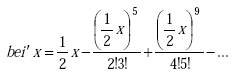(A-83)

or

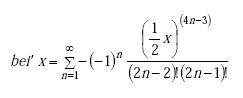(A-84)

APPENDIX A-3

COMPLETE ELLIPTIC INTEGRAL OF FIRST KIND

(A-85)

(A-86)

(A-87)

(A-88)

COMPLETE ELLIPTIC INTEGRAL OF SECOND KIND

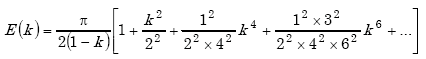(A-89)

or

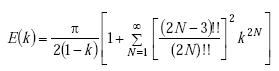(A-90)

(A-91)

(A-92)

(A-93)

where 2N!! = 2^NN!.

APPENDIX A-4

SERIES TO PARALLEL CIRCUIT TRANSFORMATION

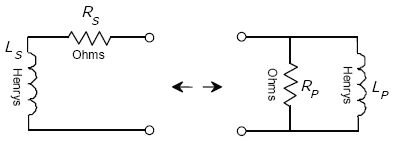
Figure A-16. Series-circuit to parallel-circuit equivalency (general).

From Figure A-16,

(A-94)

setting

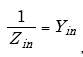(A-95)

we find

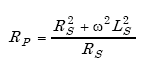(A-96)

and

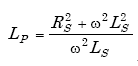(A-97)

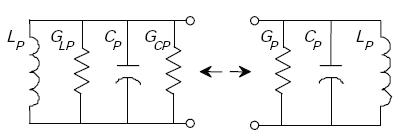
Figure A-17. Loop-series to parallel-circuit equivalency.

From Figure A-17,

(A-98)

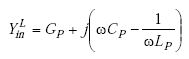(A-99)

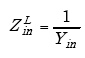(A-100)

APPENDIX A-5

TRANSFORMER MODEL INPUT IMPEDANCE

The transformed load impedance shown in equation A-68 is derived from nodal analysis of the transformer model. The transfer function is defined as the ratio of the output of a system to the input. It is thus used to find the output of a system or module for a given input.

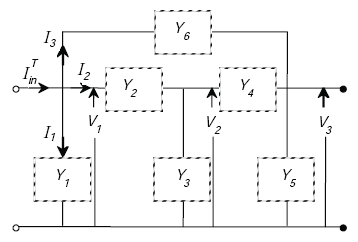
Figure A-18. Transformer nodal analysis diagram.

From Figure A-18, we find

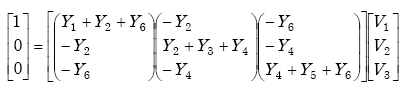(A-101)

(A-102)

(A-103)

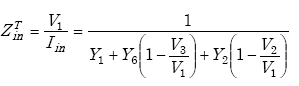(A-104)

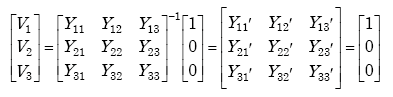(A-105)

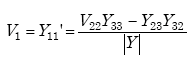(A-106)

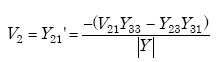(A-107)

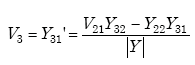(A-108)

where

(A-109)

(A-110)

(A-111)

(A-112)

(A-113)

(A-114)

REFERENCES

1. Mills, M.K. "Self Inductance Formulas for Multi-Turn Rectangular Loops Used with Vehicle Detectors," 33rd [Institute of Electrical and Electronics Engineers] IEEE VTG Conference Record, IEEE. 1983. pp. 64–73. May 1983.
2. Mills, M.K. "Self Inductance Formulas for Quadrupole Loops Used with Vehicle Detectors," 35th IEEE VTG Conference Record, IEEE. 1985. pp. 81–87. May 1985.
3. King, R.W.P. Fundamentals of Electro-Magnetic Theory. Dover Publishing, Inc. 1962. pp. 450–456.
4. Langford-Smith, F. Radiotron Designer’s Handbook. Wireless Press, Australia. 1953. pp. 219–221.
5. Johnson, W.C. Transmission Lines and Networks. McGraw-Hill Book Company, Inc. 1950. p. 85.
6. Palermo, A.J. "Distributed Capacity of Single-Layer Coils," Proceedings of the [Institute of Radio Engineers] IRE, vol. 22, no. 7. July 1934. p. 897.
7. Langford-Smith, F. op. cit., p. 221.
8. Galejs, Janis. Antennas in Inhomogeneous Media, Pergamon Press. 1969. pp. 60–64.
9. Ramo, S., J.R. Whinnery, and T. Van Duzer. Fields and Waves in Communication Electronics. John Wiley and Sons, Inc. 1965. p. 336.
10. Stratton, J.A. Electromagnetic Theory, McGraw-Hill Book Company, Inc. 1941. pp. 551–554.
11. ITT. Reference Data for Radio Engineers, 5th Edition. Howard W. Sams and Company, Inc., Indianapolis, IN. 1974. pp. 22–23.
12. Johnson, W.C. op. cit., p. 78.
13. Dwight, H.B. Tables of Integrals and Other Mathematical Data. The Macmillan Publishers. 1957. p. 184.
14. Ramo, S., et al., op. cit., p. 311.
15. Murdock, B.K. Handbook of Electronic Design and Analysis Procedure Using Programmable Calculators. Van Nostrand Reinhold Company. 1979. p. 475.
16. Dwight, H.B. op. cit., p. 171.
17. King, R.W.P. op. cit.
18. Ramo, S. et al., op. cit., p. 307.
19. Seely, S. Introduction to Electromagnetic Fields. McGraw Hill Book Company. 1958. pp. 185–186.
20. Burmeister, D. "Traffic Signal Detector Loop Location Design Installation." Illinois Department of Transportation, Division of Highways, District 6. November 1, 1988. p. 18.
21. Jefimenko, O.D. Electricity and Magnetism. 2nd Ed. Electret Scientific Co., P. O. Box 4132, Star City, WV. 1989. p. 372.
22. Grover, F.W. Inductance Calculators: Working Formulas and Tables. Dover Publications, Inc. 1962. pp. 45–46.
23. Johnson, W.C. op. cit., p. 88.
24. Ibid., p. 105.
25. Dwight, H.B. op. cit., p. 144.
26. Mills, M.K. "Inductance Loop Detector Analysis," 31st IEEE VTG Conference Record, IEEE. April 1981. p. 404.
27. Grossner, N.R. Transformers for Electronic Circuits. McGraw-Hill Book Company. 1967. pp. 176–177.

Previous | Table of Contents | Next

FHWA-HRT-06-139