Safety Effects of Horizontal Curve and Grade Combinations on Rural Two-Lane Highways

The safety effects of horizontal curves and grades on rural two-lane highways have been quantified in the American Association of State Highway and Transportation Officials (AASHTO) Highway Safety Manual (HSM), but it was not previously known whether and how the safety performance of horizontal curves and grades interact.⁽¹⁾ Furthermore, there are no established safety effects for crest and sag vertical curves, and it is unknown whether and how the safety performance of crest or sag vertical curves is affected by the presence of horizontal curves.

The objective of this study was to quantify the combined safety effects of horizontal curves and grade combinations and express the results as crash modification factors (CMFs) that can be considered for use in the AASHTO HSM.⁽¹⁾

BACKGROUND

Design criteria for horizontal and vertical alignment are presented in chapter 3 of the AASHTO Policy on Geometric Design of Highways and Streets, commonly known as the Green Book.⁽²⁾ Many State highway agencies have their own design manuals, but in terms of horizontal and vertical alignment, they closely resemble the AASHTO Green Book.

Straight road sections with no horizontal curvatures are generally referred to as "tangents" because such straight road sections are generally tangent to any horizontal curves that they adjoin.

The key design parameters for horizontal curves include the following:

• Radius of curvature.
• Length of curve.
• Superelevation.
• Transition design.

The safety effects of both radius and length of horizontal curves are addressed in CMFs developed in this current study. The safety effects of superelevation and transition design are outside the scope of the study because no data concerning these features were available at the time this study was conducted.

The fundamental design parameter for vertical alignment is the percent grade. A road section with constant percent grade, regardless of its horizontal alignment, is generally referred to as a straight grade. Where the grade of the roadway changes, the straight grade sections are normally joined by a parabolic vertical curve. Figure 1 illustrates the four types of vertical curves (two types of crest vertical curves and two types of sag vertical curves) that are used in highway design. Key design parameters for vertical curves include the following:

• Algebraic difference (A) between the initial (G₁) and final (G₂) grades.
• Length of curve (L_VC).
• K, the ratio of L_VC and A, which represents the measure of sharpness of the vertical curve.

The safety effects of each of these design parameters for vertical alignment are addressed in CMFs developed in the current study.

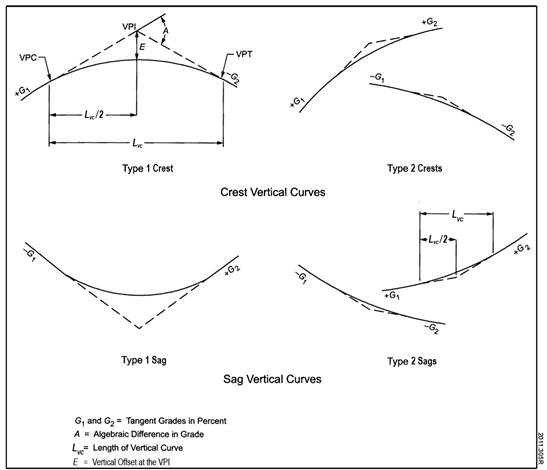
Source: AASHTO. Used by permission.

Figure 1. Illustration. Types of vertical curves.⁽²⁾

METHODOLOGY

Research was undertaken to quantify the safety effects of horizontal and vertical alignment combinations and to present them as CMFs. The complete results of this research are documented in the full report, Safety Effects of Horizontal Curve and Grade Combinations on Rural Two-Lane Highways.⁽³⁾

Database Used

The research was performed with the Highway Safety Information System (HSIS) data for State highways in Washington. This is the only data source that includes system-wide data on curve and grade geometry that can be linked to system-wide roadway characteristics, traffic volume data, and crash data. Several roadway types were considered, but only rural two-lane highways in Washington had sufficient data for which modeling efforts appeared promising.

Crash data for a 6-year period (2003 to 2008) were obtained and used in the analysis. Each crash was assigned to a particular roadway segment with particular horizontal and vertical alignment based on its assigned milepost location. Since the results of this research are intended for use in the roadway segment procedures of the AASHTO HSM, only nonintersection crashes were considered.⁽¹⁾

Of the 6,944 mi of roadway in the entire Washington HSIS database, 4,785 mi (69 percent) are on rural two-lane highways. Of these, 3,457 mi were used for analysis. Rural two-lane highways with passing or climbing lanes and segments with missing or obviously incorrect alignment data (e.g., overlapping curves) were excluded from the study. Roadway length (miles), exposure (million vehicle miles traveled (MVMT) in the 6-year period), crash frequencies, and crash rates per MVMT are shown in table 1 for specific horizontal and vertical alignment for rural two-lane highways.  

Table 1. Roadway length, exposure, crash frequency, and crash rates
for rural two-lane highways in the Washington HSIS database.

^aFor years 2003 to 2008.

N/A = Not applicable.

Analysis Approach

The safety effects of horizontal curve and grade combinations were estimated based on a cross-sectional analysis using a generalized linear model approach assuming a negative binomial distribution of crash counts and an exponential model using the combined crash data from all 6 years and selected roadway geometrics. FI and PDO crashes were modeled separately for each of the five types of horizontal curves and grade combinations. All analyses were performed using a procedure for fitting generalized linear models of SAS^® Version 9.3.⁽⁴⁾

The following parameters were considered for inclusion in each model:

• Average annual daily traffic (averaged across all 6 years).
• Segment length.
• Horizontal curve radius (R).
• Absolute value of percent grade (G).
• Horizontal curve length (L_C).
• Vertical curve length (L_VC).
• Algebraic difference between the initial (G₁) and final (G₂) grades (A; A = abs(G₁ − G₂)).
  AMENDED February 8, 2016
• Measure of the sharpness of vertical curvature (K; K = L_VC/A).
• Relevant interactions of selected parameters.

For each type of horizontal curve and grade combination, the dataset used for modeling included the roadway segments for the relevant curve and grade combination but also all level tangents (i.e., no horizontal curvature and grade < 1 percent) to serve as the base condition. Details of the statistical analysis and resulting crash prediction models are presented in the full report.⁽³⁾

Crash Modification Factors

CMFs used in the AASHTO HSM were derived from predictive models.⁽¹⁾ CMF is a factor that represents the effect on crash frequency for a given crash severity level of varying geometric design and traffic control feature of interest (or a particular combination of geometric design or traffic control feature). Each CMF has a nominal value of 1.0 for a specified base condition. CMF with a value greater than 1.0 represents a condition for which more crashes would be expected than for the base condition. CMF with a value less than 1.0 represents a condition for which fewer crashes would be expected than for the base condition. The base condition for all CMFs developed in this research is a level tangent roadway. This is consistent with the base conditions in the current AASHTO HSM.⁽¹⁾

AMENDED February 8, 2016

For each alignment type combination (as well as each FI and PDO crash), CMFs were calculated as the ratio of the predicted crash frequency for a given horizontal curve and grade combination to the predicted crash frequency for the level tangent base condition. The following subsections provide the equations for CMF in each of the five alignment categories for rural two-lane highways.

AMENDED February 8, 2016

CMFs for Horizontal Curves and Tangents on Straight Grades

The CMFs for horizontal curves and tangents on straight grades were provided in figures 2 and 3:

AMENDED February 8, 2016

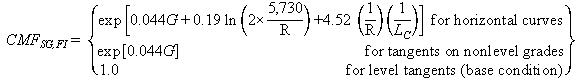
Figure 2. Equation. FI CMF for horizontal curves and tangents on straight grades.

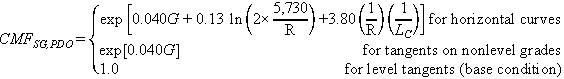
Figure 3. Equation. PDO CMF for horizontal curves and tangents on straight grades.

Where SG = straight grade.

To calculate CMF for FI or PDO crashes for a given horizontal curve on a level or nonlevel grade or a tangent on a nonlevel grade, the absolute value of G (percent), R (ft), and L_C (mi) must be substituted in figure 2 or figure 3.

CMFs for Horizontal Curves and Tangents at Type 1 Crest Vertical Curves

CMFs for horizontal curves and tangents at type 1 crest vertical curves (C1) are provided in figures 4 and 5:

AMENDED February 8, 2016

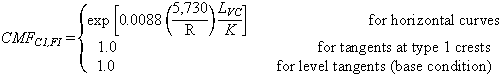
Figure 4. Equation. FI CMF for horizontal curves and tangents at type 1 crest vertical curves.

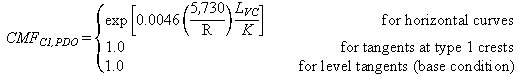
Figure 5. Equation. PDO CMF for horizontal curves and tangents at type 1 crest vertical curves.

To calculate CMF for FI or PDO crashes for a given horizontal curve at a type 1 crest vertical curve, the actual values of R (ft), L_VC (ft), and parameter K (ft/percent) must be substituted in figure 4 or figure 5.

CMFs for Horizontal Curves and Tangents at Type 1 Sag Vertical Curves

The CMFs for horizontal curves and tangents at type 1 sag vertical curves (S1) were are shown in figures 6 and 7

AMENDED February 8, 2016

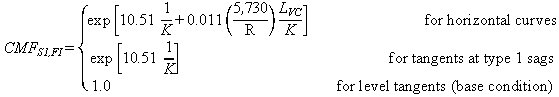
Figure 6. Equation. FI CMF for horizontal curves and tangents at type 1 sag vertical curves.

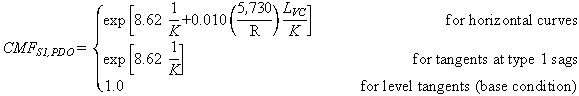
Figure 7. Equation. PDO CMF for horizontal curves and tangents at type 1 sag vertical curves.

To calculate CMF for FI or PDO crashes for a given horizontal curve at a type 1 sag vertical curve, the actual values of R (ft), L_VC (ft), and parameter K (ft/percent) must be substituted in figure 6 or figure 7.

CMFs for Horizontal Curves and Tangents at Type 2 Crest Vertical Curves

The CMFs for horizontal curves and tangents at type 2 crest vertical curves (C2) are shown in figures 8 and 9:

AMENDED February 8, 2016

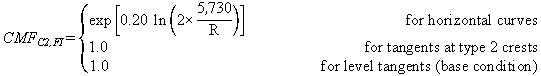
Figure 8. Equation. FI CMF for horizontal curves and tangents at type 2 crest vertical curves.

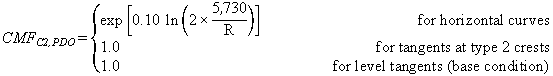
Figure 9. Equation. PDO CMF for horizontal curves and tangents at type 2 crest vertical curves.

To calculate CMF for FI or PDO crashes for a given horizontal curve at a type 2 crest vertical curve, the actual value of R (ft) must be substituted in figure 8 or figure 9.

CMFs for Horizontal Curves and Tangents at Type 2 Sag Vertical Curves

The CMFs for horizontal curves and tangents at type 2 sag vertical curves (S2) are shown in figures 10 and 11:

AMENDED February 8, 2016

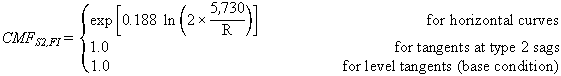
Figure 10. Equation. FI CMF for horizontal curves and tangents at type 2 sag vertical curves.

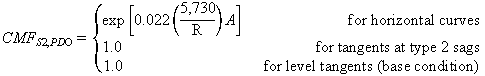
Figure 11. Equation. PDO CMF for horizontal curves and tangents at type 2 sag vertical curves.

To calculate CMF for FI crashes for a given horizontal curve at a type 2 sag vertical curve, the actual value of R (ft) must be substituted in figure 10 or figure 11, and A must be substituted in figure 11.

APPLICATION OF CMFs

To calculate the CMF values using the equations in figure 2 through figure 11, the following guidelines should be applied:⁽³⁾

AMENDED February 8, 2016

• Any horizontal curve R less than 100 ft should be treated as equal to 100 ft. This implements guidance currently presented in the AASHTO HSM.⁽¹⁾
  AMENDED February 8, 2016
• If R for a horizontal curve is greater than or equal to 11,460 ft, CMF applicable to tangents (on either level or nonlevel grades, as appropriate) should be used rather than CMF for a horizontal curve.
• For either a tangent or a horizontal curve, if the percent G for a straight grade is between -1.0 and +1.0 percent, the CMF applicable to a level grade (G = 0) should be used.
• For either a tangent or a horizontal curve, if G₁ and G₂ are between -1.0 and +1.0 percent, the CMF applicable to a straight grade that is level (G = 0) should be used rather than the CMF for a vertical curve.

The results presented in figure 2 through figure 11 provide separate CMFs for FI and PDO crashes. CMF for total crashes (i.e., all crash severity levels combined) can be computed as follows:

Figure 12. Equation. CMF for combined crash severity level.

Where:

CMF_TOT = CMF for total crashes (i.e., all severity levels combined).

CMF_FI = CMF for FI crashes.

CMF_PDO = CMF for PDO crashes.

P_FI = FI crashes expressed as a proportion of total crashes.

P_PDO = PDO crashes expressed as a proportion of total crashes.

The values used for P_FI and P_PDO must always sum to 1.0. The values of P_FI and P_PDO indicated for rural two-lane highways in AASHTO HSM table 10-3 (P_FI = 0.321 and P_PDO = 0.679) may be used, or users may develop values for P_FI and P_PDO from their agencies’ data.⁽¹⁾

Figure 13 illustrates a typical comparison of CMFs for horizontal curves on straight grades developed in this study, as shown in figure 2 and figure 3 for FI and PDO crashes, respectively, to the combined HSM CMF. The length of horizontal curve and radius were kept constant, while the percent grade was varied.

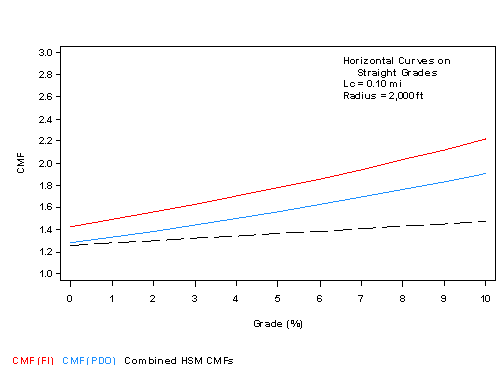
Figure 13. Graph. Comparison of CMFs developed in this study to the combined AASHTO HSM CMFs for horizontal curves and grades for fixed radius and varying percent grades.⁽¹⁾

Figure 14 is an analogous plot, where the length of horizontal curve and percent grade were kept constant, while the radius of the horizontal curve varied. The plots show that the CMF for FI crashes developed in the current study is consistently larger than the CMF for PDO crashes developed in the current study. This represents an advance in knowledge compared to the AASHTO HSM, which treated the CMFs as equal for all severity levels.⁽¹⁾ The plots also show that the new CMFs are generally larger than the combined HSM CMFs, except that the new CMF for PDO crashes is smaller than the existing CMFs for horizontal curves with short radii.

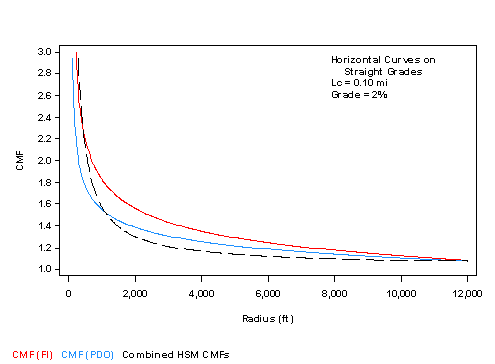
Figure 14. Graph. Comparison of CMFs developed in this study to the combined AASHTO HSM CMFs for horizontal curves and grades for fixed percent grade and varying radii.⁽¹⁾

CMF presented in figure 12 can be considered to replace the combined effect of CMF_3r for horizontal curves presented in AASHTO HSM equation 10-13 and CMF_5r for grades presented in AASHTO HSM table 10-11.⁽¹⁾ In other words, CMF_TOT is a potential substitute for the product of CMF_3r × CMF_5r in AASHTO HSM equation 10-2, which currently represents the combined total of FI and PDO crashes.⁽¹⁾ It is expected that future AASHTO HSM editions will model FI and PDO crashes separately so that CMFs for individual crash severity levels may be used directly in AASHTO HSM equation 10-2. A decision as to whether new CMFs presented in figure 2 through figure 12 should be incorporated in the AASHTO HSM will be made by AASHTO at some future time.

The AASHTO HSM also includes CMF_4r, which represents the safety effect of superelevation variance defined for any horizontal curve as the design superelevation rate for that curve recommended in the AASHTO Green Book minus the actual superelevation of the curve.^(1,2) The models developed in the current study do not account for superelevation variance, so CMF_4r should still be used even if CMF_3r and CMF_5r are replaced by the new CMFs developed in this current study.

CMF CALCULATION TOOL

A Microsoft Excel^® calculation tool has been developed to assist users in determining the values of CMFs using figure 2 through figure 12 for any horizontal curve and grade combination. The tool includes five worksheets. The names and function of each worksheet are as follows:

1. Instructions: Description of each tab and its function.
2. Tgt StraightGrade: Calculation of CMFs for tangents on straight grades.
3. HCurve StraightGrade: Calculation of CMFs for horizontal curves on straight grades.
4. Tgt VCurve: Calculation of CMFs for tangents at vertical curves.
5. HCurve VCurve: Calculation of CMFs for horizontal curves at vertical curves.
   AMENDED February 8, 2016

Worksheets 2–5 provide a table for data input by the user and a table that displays the calculated CMF values. CMF calculations are performed using figure 2 through figure 12.

Procedures for using the CMF calculation tool are as follows:

1. Open the Microsoft Excel^® calculation tool workbook at http://www.fhwa.dot.gov/publications/research/safety/hrtm2130/index.cfm.
   AMENDED February 8, 2016
2. Click on the "Instructions" tab. Instructions on how to use the calculation tool and how to input data are provided and are detailed in steps 3–5
3. Select the appropriate CMF calculation worksheet from the four available worksheets (2–5) by clicking on the tabs at the bottom of the screen display. The worksheet selected should be appropriate for the specific combination of horizontal and vertical alignment for which a CMF is to be calculated. The alignment combinations include the following:
   • Tangents on straight grades.
   • Horizontal curves on straight grades.
   • Tangents at vertical curves.
   • Horizontal curves at vertical curves.
4. Enter the applicable input data describing the horizontal and vertical alignment in the data input table. The text immediately above the data input table on each worksheet gives guidance on typical ranges of input values. Default values based on AASHTO HSM Chapter 10 are provided for P_FI and P_PDO, which must sum to 1.0.⁽¹⁾ Users may substitute local values for the P_FI and P_PDO defaults.
5. Click "Run." The computed CMF values, along with a summary of the input data, will appear on a new row added at the bottom of the results table. Users may choose to display multiple rows in the results table. Click "Reset" to refresh the results table by deleting all displayed rows.

Figure 15 shows a typical sheet from the Microsoft Excel^® calculation tool with both input data and computed results displayed.⁽⁵⁾

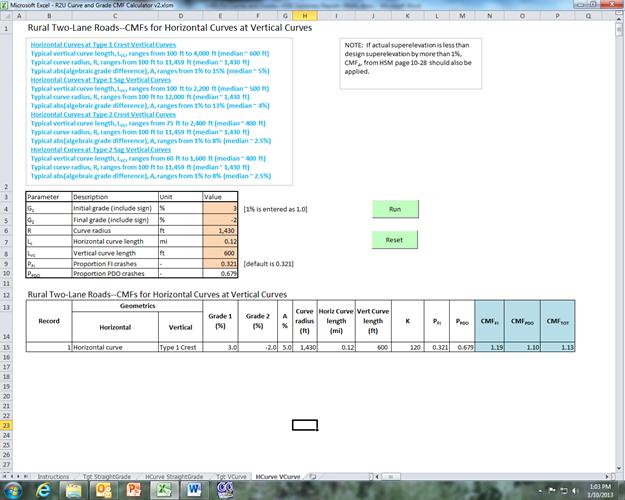
Figure 15. Screenshot. Sample screen for horizontal curve at type 1 crest CMF calculations.

REFERENCES

1. American Association of State Highway and Transportation Officials. (2010). Highway Safety Manual, 1st Edition, AASHTO, Washington, DC.
2. American Association of State Highway and Transportation Officials. (2011). A Policy on Geometric Design of Highways and Streets, AASHTO, Washington, DC.
3. Bauer, K.M. and Harwood, D.W. (2013). Safety Effects of Horizontal Curve and Grade Combinations on Rural Two-Lane Highways, Report No. FHWA-HRT-13-077, Federal Highway Administration, Washington, DC.
4. SAS^® Institute Inc. (2011). SAS^® 9.3 User's Guide, SAS Institute Inc., Cary, NC.
5. Federal Highway Administration. Highway Safety Information System, U.S. Department of Transportation, Washington, DC. Obtained from: www.hsisinfo.org.

FOR MORE INFORMATION

This research was conducted by Karin M. Bauer and Douglas W. Harwood of MRIGlobal. Chris Fees of MRIGlobal programmed the CMF calculation tool. The final report, Safety Effects of Horizontal Curve and Grade Combinations on Rural Two-Lane Highways, is published as FHWA Report No. FHWA-HRT-13-077.⁽³⁾

For more information about HSIS, contact Carol Tan, Ph.D., FHWA HSIS Program Manager, HRDS, 202-493-3315, carol.tan@dot.gov or Ana Maria Eigen, D.Sc., FHWA HSIS Program Manager, HRDS, 202-493-3315, ana.eigen@dot.gov.

AMENDED February 8, 2016