Safety Evaluation of Horizontal Curve Realignment on Rural Two-Lane Roads

This document is a technical summary of the Federal Highway Administration report Safety Evaluation of Horizontal Curve Realignment on Rural Two-Lane Roads (HRT-17-066).

Objective

The Federal Highway Administration (FHWA) established the Development of Crash Modification Factors (DCMF) Program in 2012 to address highway safety research needs for evaluating new and innovative safety strategies (improvements) by developing reliable quantitative estimates of their effectiveness in reducing crashes. The ultimate goal of the DCMF Program is to save lives by identifying new safety strategies that effectively reduce crashes and promote those strategies for nationwide implementation by providing measures of their safety effectiveness and benefit. This study evaluated realignment of horizontal curves on rural two-lane roads based on a before–after evaluation. This realignment strategy is intended to reduce lane departure crashes, especially run-off-road crashes. This evaluation developed crash modification factors (CMFs) for this strategy using state-of-the-art before–after empirical Bayes (EB) methods and then compared the results with previously developed CMFs from cross-sectional studies. The data included 39 realigned locations from California, North Carolina, and Ohio, and 56 untreated reference curves.

Typically, researchers have based studies on the effect of horizontal curve radius on a cross-sectional analysis, where they compare the safety performance of curves of differing radii. This methodology typically allows for a large potential sample of curves because there is no need to know a conversion/installation date as in a before–after study. However, a before–after methodology is generally preferable to cross-sectional for evaluating the safety effect of an infrastructure modification.⁽¹⁾

Introduction

Several studies have produced CMFs and crash modification functions (CMFunctions) for curve radii on rural two-lane roads.

The Highway Safety Manual (HSM)’s chapter for rural two-lane roads includes a CMF for horizontal curvature.⁽²⁾ The HSM based this CMF on regression analysis done by Zegeer et al.⁽³⁾ The base condition of the HSM predictive model for rural two-lane roads is a tangent, and the CMF for a curve is calculated as shown in figure 1.

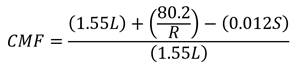
Where:

A study by Bauer and Harwood focused on the interaction of horizontal curvature and vertical curvature and grade for rural two-lane highways.⁽⁴⁾ The authors conducted a cross-sectional analysis of roadway segments from Washington State. They used 3,457 mi of road and 6 years of crash data to produce a series of CMFunctions to quantify the safety performance of various combinations of vertical and horizontal alignment. Their study classified horizontal alignment of roadway segments as follows:

• Tangent.
• Horizontal curve.

Their study classified vertical alignment of roadway segments as follows:

• Level.
• Straight grade (constant percent grade of 1 percent or more).
• Type 1 or 2 crest vertical curve.
• Type 1 or 2 sag vertical curve.

Figure 2 shows one of the CMFunctions produced by Bauer and Harwood. The function calculates a CMF for fatal and injury crashes for a horizontal curve that occurs on a straight grade (i.e., no vertical curvature). The study produced other CMFunctions for other conditions (e.g., horizontal curve on a type 1 vertical crest).

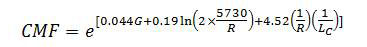
Where:

Saleem and Persaud built on the work for two-lane highways to explore the development of a CMFunction where they explored designs to flatten an existing horizontal curve.⁽⁵⁾ They focused on horizontal curves only on level grade (less than 3 percent). They used 440 curves from Washington State with radii between 100 and 11,000 ft to conduct a cross-sectional analysis and develop CMFunctions. Their functions showed that CMFs decreased (fewer crashes occurred) for scenarios in which a large radius was entertained. Furthermore, they found that the level of annual average daily traffic (AADT) on the subject segment did not influence the effect.

Previous studies have generally shown that a high curve radius is associated with few crashes. However, all published studies that have examined the safety effect of horizontal curvature were based on cross-sectional studies, which may not always have provided reliable CMFs. This illustrates the need for before–after studies, even if researchers must base those studies on a small sample to verify the results the cross-sectional studies have obtained.

Data and Methodology

The evaluation used data from California, North Carolina, and Ohio. The evaluation included the following crash types:

• Total crashes.
• Injury and fatal crashes.
• Run-off-road and fixed object crashes.
• Crashes during dark conditions.
• Wet crashes.

The evaluation included 39 realigned curves and 56 reference curves that were not realigned. Table 1 shows the summary statistics for the realigned (treatment) and reference sites.

The evaluation applied the EB methodology for observational before–after studies.⁽⁶⁾ The project team estimated safety performance functions (SPFs) used in the EB methodology through generalized linear modeling assuming a negative binomial error distribution, which is consistent with the state of research in developing these models. In specifying a negative binomial error structure, the project team estimated an over-dispersion parameter that was used in the EB methodology.

The full report includes a detailed explanation of the methodology and development of SPFs, including a description of how estimates of safety effects for each crash type was calculated.

Results

Table 2 provides the estimates of expected crashes in the after period without treatment, the observed crashes in the after period, and the estimated CMF and its standard error for all crash types considered. Although all crash categories had low sample sizes of crashes, the project team did not analyze head-on and sideswipe crashes because of the low number of crashes of these types in the study sites. The project team based the CMFs reported in table 2 on all 39 realigned curve locations. The project team also estimated the CMFs after removing the three locations the States realigned to straight segments, and the resulting CMFs were almost identical to the ones reported in table 2. The results indicate large reductions that were statistically significant at the 95-percent confidence level for all crash types analyzed.

Results pertained to a range of site characteristics, the most important of which was the range of before–after curve radii. Average degrees of curve in the before–after periods were 18.1 and 6.9, respectively (the degree of curve is mentioned here instead of radius because three curves were realigned to straight segments, which had undefined radius values but had a degree of 0.0). The average central angle of the curves was approximately 42 degrees, the average AADT at these sites was about 3,500, and the average length of the segments that States realigned was 0.1455 mi.

*Statistically significant at the 95-percent confidence level.

One intent of this evaluation was to compare results of before–after evaluations with published results from cross-sectional studies. The project team accomplished this using two different approaches. The first approach involved entering the average radii in the before–after periods along with the average segment length of the study sites to estimate CMFs based on the equations given in Zegeer et al. (for total crashes) and Bauer and Harwood (for injury and fatal crashes).^(3,4) Based on the equation given in Zegeer et al.—and assuming no spiral transition curves—the ratio of the CMF for a 6.9-degree curve to an 18.1-degree curve was 0.672 for total crashes.⁽³⁾ For the same conditions, the CMFunction in Bauer and Harwood estimated a CMF of 0.784 for injury and fatal crashes.⁽⁴⁾

The first approach was simplistic in that it did not specifically account for the fact that the relationship between CMF and curve radius and segment length was non-linear in both Zegeer et al. and Bauer and Harwood.^(3,4) To address this limitation, the project team identified a second approach. The second approach involved the following steps:

1. For each treated site, calculate CMF based on Zegeer et al. and Bauer and Harwood.^(3,4)
2. Multilily EB expected crashes in the after period for each site (expected crashes had the treatment not been implemented) with CMFs from Zegeer et al. and Bauer and Harwood.^(3,4) This product gives the expected crashes with the treatment for each site based on CMFs from these two studies.
3. Calculate the sum of expected crashes with the treatment for all sites based on the two studies.
4. The ratio of EB expected crashes with the treatment to EB expected crashes without the treatment provides an approximate CMF associated with the equations from the two studies.

Based on the second approach, the CMF from Zegeer et al. was 0.699 (for total crashes), and the CMF from the Bauer and Harwood was 0.736 (for injury and fatal crashes).^(3,4)

CMFs from the previous studies were higher than CMFs of 0.315 and 0.259 that were estimated using the before–after EB evaluation for total and injury and fatal crashes, respectively. This difference was consistent with previous studies of other treatments that seemed to indicate cross-sectional studies can sometimes underestimate the safety benefit of a treatment (i.e., overestimate the CMF). However, the project team based this before–after evaluation on a limited sample, and readers are encouraged to apply the results with prudence.

CMFunctions were estimated using results of the evaluation, and the full report details the approach. The CMFunctions indicated the CMF increased as AADT increased but decreased as the difference between the radii of the two curves increased and as the central angle increased.

CMFunctions are not presented here because the project team based them on a small site sample. However, the general indications of the CMFunction may be useful in a contemplated curve realignment—in particular, that safety benefits may increase for curves with a large central angle and where the difference in radius between the before–after period conditions is larger. This is consistent with previous cross-sectional studies (e.g., Zegeer et al. and Bauer and Harwood), which indicated safety benefits due to realignment would increase with a large increase in radius from the before–after periods.^(3,4)

Economic Analysis

The project team estimated the expected benefit due to the realignment as 1.495 injury and fatal crashes per mi-year and 1.825 property damage only (PDO) crashes per mi-year. For the benefit calculations, the project team used the most recent FHWA mean comprehensive crash costs disaggregated by crash severity and location type as a base. They developed these costs based on 2001 crash costs, and unit costs (in 2001 U.S. dollars) for injury and fatal crashes and PDO crashes in rural areas were $206,015 and $7,800, respectively.⁽⁷⁾ The project team then updated this to 2015 dollars by applying the ratio of the U.S. Department of Transportation (USDOT) 2015 value of a statistical life of $9.4 million to the 2001 value of $3.8 million.⁽⁸⁾ Applying this factor of 2.47 to the unit costs resulted in aggregate 2015 unit costs of $510,446 for injury and fatal crashes and $19,326 for PDO crashes. The expected annual benefit due to a reduced crash rate after realignment was $798,507. Based on the suggestions from USDOT, the project team conducted sensitivity analyses to obtain a low and high value for the benefits and, consequently, a low and high value for the benefit–cost (B/C) ratios.

The project team estimated the annualized cost of the treatment using the equation shown in Figure 3.

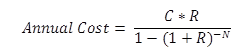
Where:

The annualized cost per year for realignment was $251,558. The project team calculated a B/C ratio of 3.17:1 as the ratio of the annual crash savings to the annualized treatment cost. The sensitivity analysis yielded a B/C range from 1.75:1 to 4.38:1.

Summary and Conclusions

Table 3 presents recommended CMFs for curve realignment on rural two-lane roads. Results pertained to a range of site characteristics, the most important of which was the range of before–after degrees of curve. Average degrees of curve in the before–after periods were 18.1 (minimum of 3.2 and maximum of 52.1) and 6.9 (minimum of 0.0 and maximum of 16.3), respectively. Average central angle of the curves was approximately 42 degrees (minimum of 1 and maximum of 117). Average AADT at the treated sites was about 3,500 (minimum of 465 and maximum of 11,917). Average length of the realigned segments was 0.15 mi (minimum of 0.03 and maximum of 0.60).

*Statistically significant at the 95-percent confidence level.

Estimated CMFunctions showed that safety benefits may be greater for curves with a larger central angle and where the difference in radius between the before–after period conditions is larger. In addition to developing CMFs using before–after evaluation, this study also compared total crash CMF with results from previous cross-sectional studies. CMFs from this before–after evaluation were lower than those estimated by two previous cross-sectional studies. As part of this effort, the North Carolina Department of Transportation conducted an analysis of crashes attributed to the curves in the study based on milepost crash reports. Their analysis revealed that relying solely on identifying crashes using the mileposts could potentially lead to significant undercounting. However, for this study, the effect of this undercounting on the CMF result was not significant. Further research is needed to understand this issue. he economic analysis yielded a B/C ratio of 3.17:1 with a range from 1.75:1 to 4.38:1. There is a need for further research with a larger sample of sites to assess the reliability of CMFs obtained from this before–after evaluation.

References

1. Gross, F., Persaud, B., and Lyon, C. (2010). A Guide to Developing Quality Crash Modification Factors, Report FWHA-SA-10-032, Federal Highway Administration, Washington, DC.
2. AASHTO. (2010). Highway Safety Manual, First Edition, American Association of State Highway and Transportation Officials, Washington DC.
3. Zegeer, C., Stewart, J.R., Council, F.M., Reinfurt, D.W., and Hamilton, E. (1992). “Safety Effects of Geometric Improvements on Horizontal Curves,” Transportation Research Record, 1356, Transportation Research Board, Washington, DC.
4. Bauer, K. M. and Harwood, D. W. (2014). Safety Effects of Horizontal Curve and Grade Combinations on Rural Two-Lane Highways, Report FHWA-HRT-13-077, Federal Highway Administration, Washington, DC.
5. Saleem, T. and Persaud, B. (2016). “Another Look at the Safety Effects of Horizontal Curvature on Rural Two-Lane Highways,” Transportation Research Board Annual Meeting Paper Compendium, Paper No. 16-6347, Transportation Research Board, Washington, DC.
6. Hauer, E. (1997). Observational Before-After Studies in Road Safety, Pergamon Press, Oxford, UK.
7. Council, F., Zaloshnja, E., Miller, T., and Persaud, B. (2005). Crash Cost Estimates by Maximum Police-Reported Injury Severity Within Selected Crash Geometries, FHWA-HRT-05-051, Federal Highway Administration, Washington, DC.
8. U.S. Department of Transportation. (2015). Guidance on Treatment of the Value of a Statistical Life (VSL) in U.S. Department of Transportation Analyses—2015 Adjustment, Memorandum, Washington, DC. Available online: https://cms.dot.gov/sites/dot.gov/files/docs/VSL2015_0.pdf, last accessed May 10, 2016.