This report describes the most comprehensive set of real-time field
measurements of bridge scour ever assembled. It represents more than
6 years of dedicated effort by the U.S. Geological Survey researchers
to collect scour data during flood events wherever they occurred in the
United States. The report will be of interest to bridge engineers and
hydraulic engineers involved in bridge scour evaluations and to researchers
involved in developing improved bridge scour evaluation procedures. Sufficient
copies will be printed to provide at least two copies to each Federal
Highway Administration (FHWA) Division Office.
T. Paul Teng, P.E.
Director, Office of Infrastructure
Research and Development
This document is disseminated under the sponsorship of the U.S. Department
of Transportation in the interest of information exchange. The U.S. Government
assumes no liability for the contents or use thereof. This report does
not constitute a standard, specification, or regulation.
The U.S. Government does not endorse products or manufacturers. Trade
and manufacturers' names appear in this report only because they are
considered essential to the object of the document.
FHWA provides high-quality information to serve Government, industry,
and the public in a manner that promotes public understanding. Standards
and policies are used to ensure and maximize the quality, objectivity,
utility, and integrity of its information. FHWA periodically reviews
quality issues and adjusts its programs and processes to ensure continuous
quality improvement.
1. Report No.
FHWA-RD-03-052
|
2. Government Accession
No.
|
3. Recipient's Catalog
No.
|
4. Title and
Subtitle
FIELD OBSERVATIONS AND EVALUATIONS OF STREAMBED SCOUR AT BRIDGES
|
5. Report Date
May 2005
|
| 6. Performing Organization
Code |
7. Author(s) David S. Mueller
and Chad R. Wagner
|
8. Performing
Organization Report No.
|
9. Performance
Organization Name and Address
U.S. Geological Survey Water Resources Division
9818 Bluegrass Parkway
Louisville, KY 40299
|
10. Work Unit
No. (TRAIS)
|
11. Contract
or Grant No.
DTFH61-93-Y-00050
|
13.
Type of Report and Period Covered
Final Report: 1993-1999
|
12. Sponsoring
Agency and Address
Office of Engineering Research and Development
Federal Highway Administration
6300 Georgetown Pike
McLean, VA 22101-2296
|
14. Sponsoring
Agency Code
|
15. Supplementary
Notes
Contracting Officer's Technical Representative: J. Sterling Jones
HRDI-07
|
16. Abstract
The variability and complexity of site conditions make it difficult
to develop methodology for predicting scour at bridges.
Laboratory investigations often oversimplify or ignore many
complexities common in the field. The U.S. Geological Survey,
in cooperation with the Federal Highway Administration and many
State highway agencies, has collected and compiled field data
on scour at bridges at 79 sites located in 17 States. These data
have been analyzed to isolate pier scour, contraction scour,
and abutment scour. The national data base contains 493 local
pier scour measurements, 18 contraction scour measurements, and
12 abutment scour measurements.
The pier scour measurements were used to evaluate 26 published
pier scour equations. The Froehlich Design, HEC-18, HEC-18-K4,
HEC-18-K4Mu, HEC-18-K4Mo (>2 millimeter), and Mississippi
equations proved to be better than the other equations for predicting
pier scour for design purposes. However, comparison of the scour
predicted from these equations with the observed scour clearly
shows that variability in the field data is not correctly accounted
for in the equations. Relations between dimensionless variables
developed from laboratory experiments did not compare well with
the field data. Analysis of the pier scour data indicated the
importance of bed-material characteristics as a variable in the
predictive equations.
A new K4 term for the HEC-18 pier-scour
equation was developed based on the relative bed-material size
(b/D50) where b = pier
width and D50 is the median bed material.
A review of published literature found 29 references to abutment
and contraction scour data; however, only a few provided complete
data sets.
Published comparisons of observed versus computed scour were
inconclusive. A detailed comparison of computed contraction and
abutment scour with field observations for two sites in Minnesota
was also inconclusive. The current methodology for computing
scour depth provides reasonable estimates of the maximum total
scour, but the individual estimates of contraction and abutment
scour did not compare well with the observed data. The accuracy
of the contraction and abutment scour equations may depend on
the degree of contraction, the flow distribution in and configuration
of the approach, and how well the hydraulic model represents
the true flow distribution.
|
17. Key Words:
Bridge scour, field data, contraction scour, abutment scour,
pier scour, local scour, debris
|
18. Distribution Statement
|
19. Security
Classif. (of this report)
Unclassified
|
20. Security Classif. (of
this page)
Unclassified
|
21. No. of Pages
134
|
22. Price
|
b is the pier width. |
is the effective pier width defined as 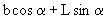 |
b1 is the bottom width in the uncontracted
section. |
b2 is the bottom width in the contracted
section. |
ca is the pier location code in
the Arkansas pier scour equation, ca=
0 for main channel piers and ca= 1 for
piers on the banks of the main channel or on the floodplain. |
D10 is the grain size of
bed material for which 10 percent is finer. |
D16 is the grain size of
bed material for which 16 percent is finer. |
D35 is the grain size of
bed material for which 35 percent is finer. |
D50 is the grain size of
bed material for which 50 percent is finer; the median grain size. |
D84 is the grain size of
bed material for which 84 percent is finer. |
D90 is the grain size of
bed material for which 90 percent is finer. |
D95 is the grain size of
bed material for which 95 percent is finer. |
D99 Is the grain size of bed material
for which 99 percent is finer. |
Dior Dis the grain size
of bed material for which i or x percent is finer. |
Dm is the mean grain size of the
bed material. |
DA is the drainage area. |
DCFM is an average of the coarse
grain sizes used by Molinas; see table 3.(1) |
Ebis the exponent on the ratio of
bottom widths for live bed contraction scour equation. |
Enis the exponent on the ratio of
roughness coefficients or live bed contraction scour equation. |
EQ is the exponent on the ratio
of discharges for live bed contraction scour equation. |
f ( ) is an undefined function of parameters
enclosed in parentheses. |
F &Fois the flow Froude
number defined as Vo/(gyo)0.5. |
Fp is the pier Froude number defined
as Vo/(gb)0.5. |
G is the acceleration of gravity. |
kis the standard normal deviate
of i. |
K is a multiplying factor that varies from
1.3 to 2.3 |
Kd is a coefficient to correct
for sediment size by Melville and Sutherland.(2) |
Ki is a coefficient to correct
the HEC-18 equation for sediment size by Molinas; see table 3.(1) |
KI is a coefficient to correct for
flow intensity defined by Melville and Sutherland.(2) |
Ks is a coefficient to correct for
pier shape defined by Melville and Sutherland.(2) |
Ksc is a coefficient for pier shape
in the Simplified Chinese equation, defined by Gao et al. to be 1 for
cylinders, 0.8 for round-nosed piers, and 0.66 for sharp nosed-piers.(3) |
KS2 is a coefficient
for pier shape used by Larras and is 1.0 for cylindrical piers and 1.4
for rectangular piers.(4) |
Ku is 1.0 for SI units and 1.81
for customary English units in the critical velocity equation. |
Ky is a coefficient to correct for
flow depth defined by Melville and Sutherland.(2) |
K1 is a coefficient based
on the shape of the pier nose, defined as 1.1 for square-nose piers,
1.0 for circular- or round-nosed piers, 0.9 of sharp-nosed piers, and
1.0 for a group of cylinders. |
K2 is a coefficient to
correct for the skew of the pier to the approach flow, defined as (cos
α + (L/b)sin α)0.65.
|
K3 is a coefficient to
correct for the channel bed condition, defined as 1.1 except when medium
to large dunes are present, and then it can range from 1.2 to 1.3. |
K4 is a coefficient to
correct for bed material size and gradation; see table 3. |
K4MuK4 coefficient
derived by Mueller.(5) |
K4MoK4 coefficient
derived by Molinas.(1) |
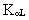 is a coefficient to correct for flow
alignment defined by Melville and Sutherland (1988).(2) is a coefficient to correct for flow
alignment defined by Melville and Sutherland (1988).(2)
|
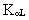 is a coefficient to correct for flow
alignment defined by Melville and Sutherland (1988).(2) is a coefficient to correct for flow
alignment defined by Melville and Sutherland (1988).(2)
|
L is the length of the pier. |
Q1is the discharge in the uncontracted
section. |
Q2 is the discharge in the contracted
section. |
S is the slope of channel in the vicinity of
the bridge. |
Vo is the approach velocity for
pier scour. |
Vc is the critical (incipient-transport)
velocity for the D50 size particle. |
Vcx is the critical (incipient-transport)
velocity for the Dx size particle. |
VR is a velocity intensity term
used by Richardson and Davis; see table 3.(6) |
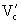 is the approach velocity corresponding to critical velocity and incipient
scour of the D50 in the accelerated flow region
at the pier.
is the approach velocity corresponding to critical velocity and incipient
scour of the D50 in the accelerated flow region
at the pier.
|
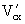 is the approach velocity corresponding to critical velocity and incipient
scour of the Dx in the accelerated flow region at
the pier.
is the approach velocity corresponding to critical velocity and incipient
scour of the Dx in the accelerated flow region at
the pier.
|
Vi is the approach velocity corresponding
to critical velocity and incipient scour in the accelerated flow region
at the pier defined by Molinas; see table 3.(1) |
Vcm is the critical (incipient-transport)
velocity for the coarse size fraction defined by Molinas; see table
3.(1) |
VLP is the live bed peak
velocity defined by Sheppard.(7) |
V2 is the velocity in
the contracted section. |
yo is the approach depth of flow
for pier scour. |
ys is the depth of scour. |
Y1 is the depth in the uncontracted
section. |
Y2 is the depth in the contracted
section. |
α is the skew of the pier to approach
flow. |
ф is a pier shape factor in Froelich's
equations |
σ is the coefficient of gradation. |
θ is the Shield's parameter. |
τ represents one or more shear stress
variables. |
ν is the kinematic viscosity in Shen's
equation (ft2/sec). |
