Simplified Techniques for Evaluation and Interpretation of Pavement Deflections for Network-Level Analysis

CHAPTER 2 - Literature Review

Introduction

An essential part of this project was to conduct an extensive literature search. While FWD load deflection data have long been used to carry out project-level analyses, using these data to conduct network-level surveys is performed less frequently. Nevertheless, the existing literature shows that several agencies are already using FWD data in their network-level pavement analysis procedures.

Some agencies have also developed procedures that may assist in the development of a simplified approach to using deflection data in a network-level analysis that links pavement structural parameters, determined through the use of FWD data to pavement performance.

A review of all available literature was duly conducted, including obtaining information from agencies outside the Unites States, to ascertain which agencies use deflection data, which approach they employ, and whether these particular approaches may be useful in the present study. All deflection parameters (measured or computed) included in this report refer to the Strategic Highway Research Program (SHRP) seven sensor positions.⁽²⁾

Literature Review Approach

Relevant literature references were reviewed on the following subjects to achieve the literature review objectives:

• Network versus project-level structural analysis: Searched for differences and similarities in deflection data collection, such as parameters used, spacing, frequency, and loading.
• Data collection: Searched and compiled information regarding data collection(sampling or systematic), section length, and spacing between tests.
• Data sources: Investigated the source of deflection data and what the data are used for in terms of network-level surveys, project-level surveys, or both.
• Data interpretation: Compiled information about how the data were analyzed (deterministic, probabilistic, combination, etc.).
• Required structural information: Identified which parameters were required and utilized for network-level structural analysis, such as the following:
  • Center deflection (D₀): The deflection at the center of the applied load.
  • Curvature index (D₀ - D_i): The difference between the center deflection and the deflection at a prescribed offset from the load center.
  • Load-normalized and temperature-corrected center deflection (₀)
  • Radius of curvature (RoC).
  • Various "AREA" values of the deflection basin.
  • Closed-form and two-layer solutions.
• Relationship to performance: Searched for literature that reports practices and research on incorporating structural evaluation of pavements based on deflections and performance measures.
• PMS implementation: Compiled information on studies about implementation of deflection-based parameters on PMS.
• Report findings on each subject: Compiled relevant information from references grouped by key topics in tabular form.

It is crucial to establish a reasonable body of knowledge on these topics to address the following:

• Establish the objectives of a structural network-level analysis.
• Determine the necessary structural information.
• Decide which conditions pavement deflections are useful for providing the required information for a network-wide structural evaluation,
• Determine performance indicators are currently used to link structural condition or integrity to the level of pavement distresses observed in the field.

Summary of Findings from Previous Studies

Table 1 provides a summary of potentially relevant agency practices for FWD data collection and use for network-level analyses identified during the literature review study (see the complete table of references in appendix A).

Table 1. Summary of useful practices for FWD use in network-level analyses.

Agencies Currently Utilizing Deflection Data for Network-Level Applications

Findings from the literature indicate that only five agencies use, or are planning to use, load deflection data directly within their PMS.

United Kingdom

The United Kingdom uses traveling deflectograph data, not FWD or dynamic load deflection data; therefore, these data are not applicable to the present study.(13,16) The traveling deflectograph does not correlate well with the FWD (or even the rolling wheel deflectometer (RWD)) due to the large differences in loading time and the Benkelman beam style apparatus involved, among other salient factors. While researchers in the United Kingdom have tried to supplement their traveling deflectograph data with FWD data, they discovered that the two do not correlate well, as expected; therefore, the FWD was dropped in favor of the traveling deflectograph. Interestingly, the old Caltrans traveling deflectograph, which was similar to the UK device, was dropped at least 30 years ago, first in favor of the Dynaflect^® and later the FWD.

Alaska

AkDOT uses a multiyear cycle for deflection readings based on ongoing pre-and post-rehabilitation projects. Their PMS approach using FWD data was only recently initiated.⁽⁹⁾ It cannot be considered a simple process since back-calculation of sorts is currently used to determine remaining life. How well AkDOT's FWD evaluation procedure actually translates to pavement distresses, and therefore to pavement life expectancy, remains to be seen. Alaska's application of load deflection data within their PMS is relatively new. Accordingly, a few more years' worth of data will be needed to evaluate structural versus performance correlations. At the time this report was written, AkDOT gathered over 300 mi (483 km) of FWD data on the Parks Highway. These data were subsequently used as an example of how to incorporate the simplified methodology developed herein and will be shown later in this report.

Conversely, the methodology used to calculate the subgrade "seed" modulus using the AkDOT procedure is straightforward and immediately useable as a stand-alone parameter. Therefore, it can be used to correlate the subgrade modulus from the LTPP FWD database to see how well that particular approach (i.e., a nonlinear subgrade modulus model) relates to the various performance indicators in the mature LTPP database. The AkDOT procedure currently applies to flexible pavements only; however, rigid pavements may be investigated using the same subgrade modulus closed-form back-calculation process.

Texas

TxDOT currently uses deflection data in their PMS for flexible pavements only (district optional). ^{(See references 10, 11, 17, and 18.)} The publication Incorporating a Structural Strength Index into the Texas Pavement Evaluation System has been in use since its publication in 1988 in some of Texas's districts.⁽¹⁰⁾ It is currently used for relatively thin asphalt-surfaced pavements in 4 of 13 districts in Texas - Fort Worth, Houston, San Antonio, and Pharr. It is expected that the entire State will soon use the newer process shown in table 1.⁽¹⁰⁾

In an older TxDOT method, network-level deflection basins were collected at selected locations in the State to determine averages and ranges for a variety of pavement thicknesses and subgrade types. Basin parameters were developed and used in lieu of a back-calculation approach due to the lack of pavement structural data (i.e., number of layers, layer thicknesses, and material types). The greatest drawback to this approach is that it does not provide an indication of remaining structural life or bearing capacity. This approach essentially uses two basin parameters: SCI and W7, which is the deflection measured 6 ft (1.83 m) from the FWD load center. SCI is the difference between the deflections measured at the center of the load plate and the deflection measured 12 inches (304.8 mm) from the load plate. From these two parameters, an SSI is determined from one of three tables: one for surface treated pavements, one for thin asphalt pavements, and one for intermediate and thick asphalt pavements. SSI is further adjusted for traffic and rainfall levels to arrive at a final SSI. SSI ranges from 100 for a 100 percent structurally adequate pavement to zero for a 100 percent structurally inadequate pavement (meaning zero percent adequacy). This approach allows the user to determine where the inadequacies lie, whether within the subgrade or somewhere within the pavement structural section itself, above the subgrade.

Virginia

VDOT recently began using deflection data in their PMS, covering the entire network on a 4- to 5-year cycle for both flexible and rigid pavements.⁽¹²⁾ The procedure is simple and straightforward. However, since it is relatively new, the current study will have to evaluate the relationship of Virginia's structural determination procedures to pavement performance data in the LTPP database.

In developing the VDOT method, a two-phase evaluation of a proposed network-level structural evaluation technique was carried out in 2007 and 2008. Both phases were restricted to interstate pavements. In phase I, only I-64 and I-77 were included in the study. The results looked promising, so phase II was initiated on the remainder of Virginia's interstate system. A final report was published in 2008, which concluded that network-level deflection testing could be used to address network needs in terms of rehabilitation strategies and funding management decisions.⁽¹²⁾ The author further suggested that the network-level structural analysis should be expanded to include Virginia's primary network.

Pavement types in the study included flexible, rigid, and composite pavement structures. For flexible pavements, the analysis was conducted according to the 1993 AASHTO Guide for Design of Pavement Structures. ⁽⁸⁾ For rigid and composite pavements, the analysis was conducted according to the 1998 Supplement to the AASHTO Guide for Design of Pavement Structures: Part II - Rigid Pavement Design and Rigid Pavement Joint Design.⁽¹⁹⁾

For flexible pavements, the resilient modulus (M_r) is first calculated according to the 1993 AASHTO Guide for Design of Pavement Structures.⁽⁸⁾ The effective pavement modulus (E_p) is calculated from the center deflection and subgrade modulus, also according to AASHTO procedures. Finally, an effective structural number (SN_eff) is determined from E_p and the total pavement thickness above the subgrade.⁽⁸⁾

For rigid and composite pavements, the deflection basin AREA and the static modulus of subgrade reaction, k, are used to quantify overall structural condition.

A cumulative distribution curve of SN_effand M_r was developed for all flexible pavements in the study. Similar curves were developed for center deflections and deflection basin AREA for rigid pavements. These distribution curves are used to identify structurally weak areas of the network for further project-level investigation.

One factor that contributed to the overall success of this approach is the availability of pavement layer data (thicknesses, material types, etc.) in VDOT's Highway Traffic Record Information System database.⁽²⁰⁾ Also noted were rather high subgrade Mr in the cumulative distribution curves. The 50th percentile value of the subgrade stiffness was around 12,500 psi (86,125 kPa). This may have been due in part to the presence of rigid or semi-rigid layers in the subgrade, which the AASHTO method does not address, and in part due to the typical non-linear behavior of cohesive subgrades (with a lower effective modulus under the load than at increasing distances from the load). The 1993 AASHTO Guide for Design of Pavement Structures equations utilize the outer deflection sensors to characterize the subgrade modulus, not the true effective modulus of the subgrade under the load.⁽⁸⁾

South Africa

The Republic of South Africa uses FWD testing at 656-ft (200-m) intervals to ascertain the bearing capacity of three roadway "zones" or layers (surface, base, and subgrade). The methodology relies on direct deflection basin parameters, not back-calculation.⁽¹⁴⁾ A benchmarking technique was developed to relate direct deflection values and basin parameters to the structural condition of the pavement at both the project and network levels. This benchmarking technique can be used in the absence of detailed information regarding pavement composition.

The South African method correlates FWD deflections to structural layers or zones within the pavement structure. These zones are numbered 1 through 3, where zone 1 corresponds to the materials closest to the load plate within the pavement structure, extending out to 11.7 inches (300 mm) in terms of the deflection basin (and probably somewhat less in terms of depth within the structure). In zone 2, the inflection point in the deflection basin occurs and generally lies from < 1 to 2 ft (< 0.305 to 0.61 m) in depth below the pavement surface. Zone 3 extends from approximately 2 to 6.5 ft (0.61 to 1.98 m) from the center of the load plate and thus represents the deepest layers in the pavement structure - primarily the subgrade.

In the South African method, the following deflection parameters and associated pavement structural zones are represented:

• D₀, or the maximum deflection as measured at the center of loading (also known as center deflection) is correlated to all three zones, since it represents the response of the entire pavement structure.
• RoC is correlated to zone 1 (the upper pavement layers) and is derived using the equation in figure 1.
• The base layer index (BLI) is correlated to zone 1 and is calculated using the equation in figure 2.
• The middle layer index (MLI) is correlated to zone 2 and is calculated using the equation in figure 3.
• The lower layer index (LLI) is correlated to zone 3 and is calculated using the equation in figure 4.

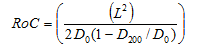
Figure 1. Equation. Calculation of RoC

Figure 2. Equation. Calculation of BLI

Figure 3. Equation. Calculation of MLI

Figure 4. Equation. Calculation of LLI

Where:
L = Diameter of the load plate of the FWD (mm).
D₀ = Deflection at center of load plate (mm).
D₂₀₀ = Deflection at 8 inches (200 mm) from the center of the load plate (mm).
D₃₀₀ = Deflection at 12 inches (300 mm) from the center of the load plate (mm).
D₆₀₀ = Deflection at 24 inches (600 mm) from the center of the load plate (mm).
D₉₀₀ = Deflection at 36 inches (200 mm) from the center of the load plate (mm).

These deflection bowl parameters are related to a structural condition rating according to the structural condition and the type of base layer, as described in table 2, extracted from Horak's "Benchmarking the Structural Condition of Flexible Pavements with Deflection Bowl Parameters."⁽¹⁴⁾

The basin parameters LLI, MLI, and BLI are plotted against stationing for a particular roadway to facilitate the structural assessment procedure. This plot of structural condition is often used in conjunction with visual assessments to determine the type of rehabilitation required to restore the pavement to a good condition.

Table 2. Structural condition associated with deflection bowl parameters.(14)

The surface modulus is calculated at the various sensors and plotted against distance from the load plate to assess nonlinearity. The standard Boussinesq equations are used for this purpose. Points where the surface modulus increases with increasing distance from the load center are regarded as "stress softening." If the surface modulus is similar for all measured deflections, the subgrade is regarded as linear-elastic. Decreasing surface modulus with increasing distance from the load center indicates a "stress stiffening" subgrade.

Agencies Utilizing Deflection Data in a Manner Potentially Useful to Enhance Network-Level PMS Applications

In addition to the previously listed agencies that already utilize load deflection data within their PMS, the following agencies use deflection data with potential network-level PMS applications:

• Caltrans: Currently uses deflection data for project-level pavement analysis and design only; however, the design method is simple and straightforward and was therefore tried during phase 2 of this study as a potential network-level PMS tool. ⁽³⁾
• KDOT: This approach is simple and straightforward. If the equations can be used to regress against LTPP performance measures, this could have been tried; however, since KDOT used this approach for flexible pavements only and only in one district for a trial project, the methodology was not further investigated.⁽⁷⁾

The following publications do not describe deflection data applications of specific agencies, but they are relevant to the scope of this project:

• NCHRP Project 10-48: This study was similar to the current study, and it utilized the LTPP database.⁽¹⁾ Equations cover flexible, composite, and rigid pavements as deflections relate to performance.⁽⁵⁾
  
  
• Temperature Predictions and Adjustment Factors for Asphalt Pavement (FHWA-RD-98-085): This study applies to asphalt temperature corrections and mid-depth temperature determinations for asphalt pavements only (not needed for concrete but likely applicable if needed).⁽⁶⁾ The equations found in this publication are potentially useful for performance measures that relate FWD center deflection to pavement performance. However, after regressing against both temperature-corrected and temperature-uncorrected values of center deflection (D₁) (or their inverse), it was determined that no improvement in any of the logistic models resulted.⁽⁶⁾
  
  
• Use of FWD in the Network Level Pavement Condition Survey: This study utilizes center deflection and measures of curvature, along with roughness, rutting, and skid resistance. ⁽¹⁵⁾ Center deflection (or its inverse) was utilized during this research, with some (but not universal) success. The results are presented later in this report.
  
  

Identified Techniques for Simplified Evaluation and Analysis

Based on the literature review and summary of useful practices presented in table 1, a list of deflection techniques was created. Several techniques were considered to be applicable to the scope of this project and were selected for further analysis. The following techniques and equations were selected when applicable:

1. D₁, measured at the center of the load plate in millimeters. (See references 14, 3, 7, 15, and 21.)
2. Direct deflection basin, D₁ through D₇, where D_i is the deflection measured at sensor i = 1 through 7 according to SHRP's seven sensor positions. ^(2,21)
3. Curvature index (CI)(see figure 5). ^(14,15,21)

   
   Figure 5. Equation. Calculation of CIi

   Where D_i is the deflection measured at sensor i = 1 through 7
4. Shape indicator (F) (see figure 6). ⁽²¹⁾

   
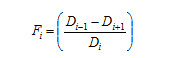
   Figure 6. Equation. Calculation of Fi

   Where i is the sensor 1 through 7.
5. Slope variance (S) (see figure 7). ⁽²¹⁾

   
   Figure 7. Equation. Calculation of Si.

6. Reciprocal indicator (I) (see figure 8).⁽²¹⁾

   
   Figure 8. Equation. Calculation of Ii

   Where i is the sensor 1 through 7.

7. Rectangular area indicator (RA) (see figure 9).⁽²¹⁾

   
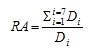
   Figure 9. Equation. Calculation of RA

   Where i is the sensor 1 through 7.

8. Trapezoidal area indicator (TA) (see figure 10).⁽²¹⁾

   
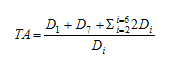
   Figure 10. Equation. Calculation of TA

   Where i is the sensor 1 through 7

9. SN_eff(see figure 11). ^(17,18,7)

   
   Figure 11. Equation. Calculation of SNeff.

   Where D is the total pavement layer thickness above the subgrade (mm) and Ep is the effective pavement modulus, computed using the equation in figure 12.

   
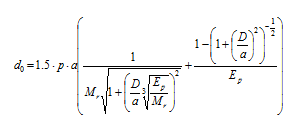
   Figure 12. Equation. Calculation of d₀.

   Where d₀ is deflection at the center of the load plate (mm), P is load plate pressure (MPa), a is load plate radius (mm), D is pavement layers thickness above subgrade (mm), and Mr is the resilient modulus, given by the following expression:

   
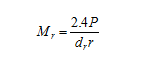
   Figure 13. Equation. Calculation of Mr.

   Where Mr is resilient modulus (MPa), P is applied load (kN), dr is deflection at a distance r from the center of the load (mm). r is chosen as the distance to the seventh sensor

10. Deterministic-empirical back-calculation model (closed form solution) for effective subgrade modulus (Hogg model).(4)

    
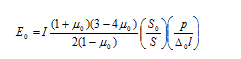
    Figure 14. Equation. Calculation of E0.

    Where E0 is subgrade modulus (effective) (MPa), μ0 is Poisson's ratio for subgrade, S₀ is the theoretical point load stiffness (MPa), S is the pavement stiffness (MPa), P is applied load (kPa), Δ₀ is the deflection at center of load plate (mm), L is the characteristic length (mm), and I is the influence factor. ⁽⁴⁾

11. Radius of curvature, shown in figure 1 (page 14) for completeness. ⁽¹⁴⁾
12. Elmod, nonlinear subgrade parameters. ⁽²²⁾

    
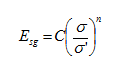
    Figure 15. Equation. Calculation of Esg.

    
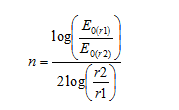
    Figure 16. Equation. Calculation of n.

    
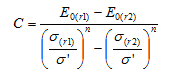
    Figure 17. Equation. Calculation of C.

    
    Figure 18. Equation. Calculation of E_0(r).

    
    Figure 19. Equation. Calculation of σ_(r)

Where:

E_sg = Subgrade modulus (kPa).
C = A layer constant, n is a layer constant representing the nonlinearity of the subgrade.
σ = Principle stress (MPa).
σ' = Reference stress (14.5 psi (0.1 MPa)).
E_0(r) = Surface modulus at distance r from load center (MPa).
r = Horizontal distance from load center (mm).
z = Vertical depth with respect to the pavement surface (mm).
σ_(r) = Principle stress at depth z (assuming z = r).
μ = Poisson's Ratio, d_(r) is deflection at distance r from load center (mm).
P = Applied load on pavement surface (MPa).
R = Distance to evaluation point (R² = r² + z²).
θ = Angle with respect to vertical axis through load center.

In addition to the parameters mentioned, the load transfer efficiency (LTE) value was calculated for rigid pavements. There are two ways of calculating LTE - in one method, the FWD test is performed at the slab before the joint (joint approach), and in the second method, the FWD test is performed at the slab after the joint (joint leave). An analysis of both was conducted, and the values were close to each other. Therefore, for simplification, only one LTE value was chosen. The option was for the first method with LTE at the joint approach because it does not require any modification on the configuration of the FWD. The LTE at joint approach is referred to as "LTEA" in this report and was calculated as the ratio of the deflection at the third sensor (12 inches (304.8 mm) from the center of the load) and the deflection at the center of the load.

CONCLUSIONS FROM THE LITERATURE REVIEW

Several successful techniques for use in network-level PMS applications were identified through the literature search. A few highway agencies have been using deflections as part of their network condition assessment. Among those, Texas, Virginia, and South African approaches were selected for further investigation in succeeding tasks with little or no modification. In addition, there were several techniques that could be utilized in the present study even though these techniques were not used in a network-level PMS. Combining all sources available, a list of potential applicable techniques that are relevant to the scope of this project was created as a result of the literature review and is shown in table 1. These deflection techniques formed the basis for the analyses carried out in this project.