Estimation of Key PCC, Base, Subbase, and Pavement Engineering Properties From Routine Tests and Physical Characteristics

PDF Version (4.44 MB)

PDF files can be viewed with the Acrobat® Reader®

CHAPTER 5. MODEL DEVELOPMENT (6)

Table 21. Regression statistics for selected prediction model for 28-day PCC cylinder strength.

The model statistics for table 21 are as follows:

• RMSE = 871 psi.
• R² = 0.5444 percent.
• N = 42.

Table 22. Range of data used for 28-day PCC cylinder strength.

Figure 133. Graph. Predicted versus measured for 28-day cylinder compressive strength model.

Figure 134. Graph. Residual error plot for 28-day cylinder compressive strength model.

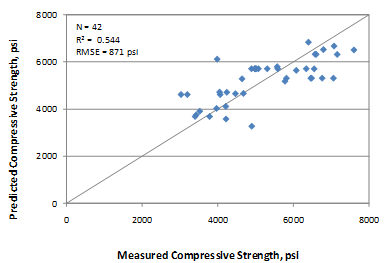
The recommended 28-day compressive strength model is as shown in figure 135.

Figure 135. Equation. Prediction model 1 for f_c,28d.

Where:

f’_c,28d= 28-day compressive strength, psi.

w/c = Water to cementitious materials ratio.

CMC = Cementitious materials content, lb/yd³.

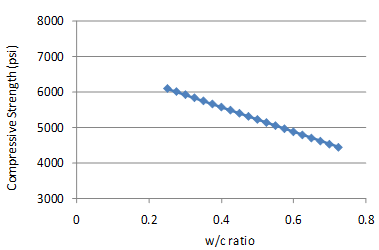
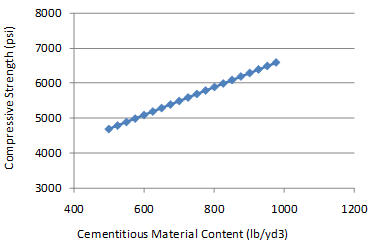
Figure 136 and figure 137 show the sensitivity of this model to w/c ratio and CMC. The change in compressive strength appears reasonable for both of the parameters for the range of values evaluated. They are also consistent with the data in the database. Within practical ranges, a change in CMC from 500 to 650 lb/ft³ increases the 28-day strength from approximately 4,700 to 5,300 psi for a w/c ratio of 0.4. Likewise, a decrease in the w/c ratio from 0.5 to 0.35 increases the strength from 4,700 to 5,200 psi.

Figure 136. Graph. 28-day compressive strength model sensitivity to w/c ratio.

Figure 137. Graph. 28-day compressive strength model sensitivity to CMC.

Compressive Strength Model 2: Short-Term Cylinder Strength Model

Cylinder strength data were available for the SPS sections at pavement ages of 14 days, 28 days, and 1 year for a majority of the sections. Although two sections with strength data at 10 years were available, data in the model were limited for ages up to 1 year. Therefore, this model predicts the strength up to an age of 1 year.

Since this model utilizes only SPS data, a large set of independent variables was available for evaluation. Additionally, it is likely that this model will be used after approval of the mix design for a project or possibly even after initial construction, during which time more mix design parameters will be known for accurate prediction. The model developed includes pavement age as an independent parameter. Because the dataset includes multiple measurements or repeated readings of the same section, this parameter has been treated with a hierarchical modeling approach.

This model was established as shown in figure 138.

Figure 138. Equation. Prediction model 2 for f_c,t.

Where:

f_c,t = Compressive strength at age t years, psi.

CMC = Cementitious materials content, lb/yd³.

w/c = Water to cement ratio.

uw = Unit weight, lb/ft³.

t = Short-term age, years.

The regression statistics for this model are presented in table 23, and details of the range of data used to develop the model are presented in table 24.

Table 23. Regression statistics for short-term cylinder strength model.

The model statistics for table 23 are as follows:

• RMSE = 789 psi.
• R² = 0.666 percent.
• N = 79.

Table 24. Range of data used for short-term cylinder strength model.

The model was developed using 79 data points, and the prediction has an R² value of 66.6 percent and an RMSE value of 789 psi. The reason for an improved R² compared to the 28-day strength model is not clear from these analyses. Figure 139 and figure 140 show the predicted versus measured plot and the residual plot, respectively.

Figure 139. Graph. Predicted versus measured for short-term cylinder compressive strength model.

Figure 140. Graph. Residual errors for short-term cylinder compressive strength model.