Simulator Study of Signs for A Complex Interchange and Complex Interchange Spreadsheet Tool

PDF files can be viewed with the Acrobat® Reader®

CHAPTER 4. DECISION TOOL TO DEFINE AND QUANTIFY INTERCHANGE COMPLEXITY

Because complexity is typically a qualitative characteristic, the ability to objectively evaluate the complexity of an interchange is somewhat difficult. This difficulty is compounded when trying to compare the complex features of multiple interchanges. This chapter discusses the spreadsheet decision tool developed as a method of quantifying and comparing the complexity of freeway interchanges in the United States. The initial discussion focuses on the steps that guided researchers in developing the spreadsheet, which is then followed by a description of the spreadsheet itself and how practitioners can use it to evaluate the complexity of interchanges under their consideration. The chapter also contains a review of the results researchers obtained from the spreadsheet in an evaluation of the complexity of 28 existing interchanges in 11 States; these study sites ranged from relatively simple to very complex, and results indicate that the spreadsheet generated scores that were generally consistent with researchers' qualitative estimation of the sites' relative complexity. The concluding section of the chapter contains a discussion on what the spreadsheet results mean and how they can be interpreted.

More details on the development of the spreadsheet decision tool are provided in appendix B, and detailed descriptions of each study site can be found in appendix C.

INITIAL SPREADSHEET DEVELOPMENT

Team Discussions

Initially, the research team discussed a variety of methods to develop a format that could apply a consistent set of criteria to measure complexity. A large number of potential variables were considered: geometric design variables, traffic control device variables, driver workload variables, and other categories. Researchers also discussed the basis on which the following variables would be included:

• Interchange-wide variables (e.g., number of levels).
• Route-specific variables (e.g., number of decision points/ramps to travel from an origin to a destination).
• Ramp-specific variables (e.g., left-side or multilane exit).

Finally, researchers discussed how the variables should be scored. That is, what quantity of a particular variable is considered to add complexity, and how does that compare to the complexity of other variables? Individual variables could be assigned threshold values for complexity, and they could be weighted to reflect their complexity relative to other variables. The variables could also be compared to values in the 2011 AASHTO Green Book.⁽²⁾

Given all of these considerations, researchers compiled a list of noteworthy variables and assigned proposed values and weights to them for presentation to practitioners to obtain their feedback on the usefulness and meaningfulness of the initial version of the spreadsheet tool.

The worksheet included 26 variables divided into the following three categories:

• Roadway geometry variables are as follows:
  • Number of concurrent routes.
  • Number of levels.
  • Exit ramps per mile.
  • Entrance ramps per mile.
  • Left exits per mile.
  • Left entrances per mile.
  • Exit ramps with multiple destinations per mile.
  • Multilane exit ramps per mile.
  • Optional/shared exit lanes per mile.
  • Exit only lanes per mile.
  • Lane balance condition.
  • Auxiliary lane as percent of minimum distance (in ft).


• Driver workload challenges variables are as follows:
  • Is the left shoulder less than the minimum width?
  • Is the right shoulder less than the minimum width?
  • Is there a loop on the exit ramp?
  • Is there a taper speed-change lane on the exit ramp?
  • Is there a taper speed-change lane on the entrance ramp?
  • Is the number of general purpose lanes greater than four?


• Driver expectancy violations variables are as follows:
  • Is the ramp straight while the main lanes are curved?
  • Are the approaching main lanes curved (resulting in difficulties in aligning arrows on signs)?
  • Is there an entrance within minimum distance downstream of this entrance?
  • Is there a short (less than 0.5 mi) weaving section between the entrance and the downstream left exit?
  • Is there an entrance ramp followed closely by an exit, and is the auxiliary lane missing? (Based on Green Book figure 10-68.)⁽⁴⁴⁾
  • Are there more exit lanes than through lanes?
  • Are there more entrance lanes than through lanes?
  • What is the number of missing legs?

Expert Panel Discussion

In January 2011, TTI conducted an expert panel discussion. Researchers wanted the panel to help identify factors that contribute to the driving complexity of an interchange area and to give their opinion on lists of variables already identified during the research as contributing to complexity. This discussion was limited to design and geometric variables and did not address existing signing or other traffic control devices currently installed at the interchanges. In addition to the four members of the TTI research team, the panel was also composed of six practitioners: three from State transportation, two from FHWA, and one from a State turnpike authority.

Overall, the panel thought the three categories of variables were a good fit for addressing interchange complexity, but they noted that the workload and expectancy categories were related (e.g., when driver expectancy is violated, it increases the workload for the driver and increases the amount of signing needed).

It was further suggested that workload is primarily driven by the density of decisions that a driver must make within an interchange area. In this case, the example stated was that if the decision points for several major destinations were within the interchange area, the workload would be significantly increased. Panelists stated that workload can be reduced through interchange design by spreading the decision points along the corridor and that addressing variables within the design category could eliminate complexity from both workload and expectancy violations. This point emphasizes the need for early coordination of geometric design and signing needs.

Prior to presenting the list of variables to the panel, researchers discussed how to assess the complexity of each of the 26 items listed and how to meaningfully and objectively compare the effects of each variable to the others on the list. Researchers discussed this issue with the panelists, along with some initial ideas on how to accomplish that comparison. The panelists echoed that sentiment and provided their comments and recommendations on how to assess each variable individually and comparatively in a revision of the list.

The panelists offered their suggestions on which variables were important and what their relative weights and scores should be, and they discussed which variables should be added or removed from the initial list of 26 characteristics. Based on the feedback, researchers revised the spreadsheet into its current version, which is described in the "Spreadsheet Tool" section in this chapter.

DEPARTMENT OF TRANSPSORTATION SITES

To determine how well the spreadsheet tool would evaluate interchanges, the research team issued a request to State transportation departments for locations of the most complex interchanges in their respective States. The research team received responses from 11 States documenting 35 interchanges. The 11 States and the number of interchanges are as follows:

• Arizona: Three interchanges.
• Delaware: Three interchanges.
• Georgia: Four interchanges.
• Indiana: Three interchanges.
• Iowa: Three interchanges.
• Maryland: Two interchanges.
• New York: Six interchanges.
• Ohio: Three interchanges.
• Oregon: Two interchanges.
• South Carolina: Three interchanges.
• Virginia: Three interchanges.

After reviewing the information provided by the State transportation departments, the research team used 28 of the interchanges for processing in the spreadsheet. Six of the remaining interchanges (one in Georgia, one in Maryland, and four in New York) contained more than four approaches, which is the capacity of the spreadsheet, while the last site (in Indiana) was not used because of poor image quality on both the aerial and street view pictures available in the Google Earth^® mapping service database due to in-progress construction at the time the images were recorded. The locations of the study sites are summarized in table 15; those not used in the spreadsheet tool development are noted.

Table 15. Summary of study sites.

Name	Location
AZ-1	I-10/I-17/US-60
AZ-2	I-10/SR 51/Loop 202
AZ-3	I-17/SR 69
DE-1	I-95/SR 1/SR 7/Churchmans Road
DE-2	I-95/I-295/SR 141
DE-3	I-295/US-13
GA-1*	I-85/I-285 (southwest of Atlanta)
GA-2	I-85/I-285 (northeast of Atlanta)
GA-3	I-85/SR 316
GA-4	I-75/I-16/US-23/SR 401
IN-1	I-65/I-80/I-94
IN-2*	I-70/I-465 (West Leg)
IN-3	I-69/I-465/Binford Boulevard
IA-1	I-35/I-80/I-235 (West Junction)
IA-2	I-380/US-30
IA-3	I-29/I-129 and US-20/US-75
MD-1	I-95/I-695
MD-2*	I-95/495 (Capital Beltway) at I-295/MD 210
NY-1	I-95/I-287/Route 1/Midland Avenue
NY-2*	I-287/I-684/Hutchinson River Parkway
NY-3	Route 9 and Route 44/55
NY-4*	I-890 Exits 4A, 4B, and 4C
NY-5*	I-95/I-278/I-295/I-678/Hutchinson River Parkway (Ref. Route 908A)/Bruckner Boulevard/Zerega Avenue
NY-6*	I-678/Grand Central Parkway (Ref. Route 907M)/Jackie Robinson Parkway (Ref. Route 908B)/Union Turnpike
OH-1	I-90/I-77
OH-2	I-71/I-670
OH-3	I-75/I-71/US-50
OR-1	I-5/I-405/US-30
OR-2	I-5/I-84/US-30
SC-1	I-26/I-126/Bush River Road
SC-2	I-385/I-185 (Toll)/US-276
SC-3	I-77/US-21
VA-1	I-95/I-495/I-395
VA-2	I-395/SR 27
VA-3	I-64/I-264/I-664/SR 13/58/191/460

*Indicates not included in the spreadsheet evaluation.

SPREADSHEET TOOL

The revised spreadsheet decision tool focuses on the following topics:

• Three interchange-wide characteristics.
• A selection of cross section characteristics at the terminus of the speed-change lane of each ramp.
• Ramp-specific characteristics that are dependent on whether the ramp is an entrance ramp or an exit ramp.

A goal during spreadsheet development was to have a format that would be easy for practitioners to understand and use. The format is based on characteristics of each ramp in the interchange. The intent is to document the decision points, along with the associated pieces of information to be processed, that a through driver would encounter while driving on that route from one end of the interchange to the other. The spreadsheet is designed to accommodate up to four routes, which are labeled to correspond to the four cardinal compass directions: NB, southbound (SB), EB, and WB. This format allows users to enter the variables for each ramp that exists along any of the four routes, and the spreadsheet processes a series of calculations to convert those site characteristics into an interchange complexity score that can be compared to other interchanges.

After users enter all of the variables, the spreadsheet calculates a complexity score for each route and for the entire interchange. The maximum possible score for a route and for an interchange overall is 1,000 points. The theoretical minimum is zero points, but the practical minimum is 10 points, which is the score given to any interchange with two levels. The "User Inputs" section in this chapter describes the process of completing the spreadsheet with the revised set of characteristics.

Spreadsheet Development

Researchers entered the information on all 28 study sites into the spreadsheet tool, taking measurements and observations from Google Earth^®. While entering the information into the spreadsheet, researchers also monitored the performance of the spreadsheet, checking that each of the dozens of equations processing a particular site contained the proper operators and referenced the correct data. As the data were entered, researchers made changes to equations as needed to produce the correct results. Researchers also considered the scores that were generated as the information for each interchange was entered to begin developing an appreciation of how well the spreadsheet identified the relative complexities of the study sites. A discussion of the complexity scores and their components is provided in more detail in the later sections of this chapter and in appendix B.

In addition, researchers reviewed the format and layout of the spreadsheet for its ability to receive data in a manner that would be intuitive and straightforward for the user. To use the spreadsheet, a user must enter a series of values into the appropriate cells for each ramp on each approach. The research team decided to use shading with colors to indicate the purpose of a cell; the color-coded cells in the spreadsheet guide the user to differentiate between cells that require user input and cells containing labels, equations, and visual boundaries between sections of the spreadsheet. A set of step-by-step instructions is provided in a separate tab of the spreadsheet.

User Inputs

To begin, the user enters basic descriptive information about the interchange (e.g., city and State and primary and secondary routes of the interchange). Next, the user enters the length of the study corridor in each direction measured from the beginning of the most upstream ramp of the interchange to the end of the most downstream ramp. Finally, the user enters the number of vertical levels in the interchange and the number of missing movements for each direction. A missing movement is the condition in which a direct path from one approach to another does not exist; two examples of missing movements are shown by the yellow lines in figure 38. Drivers traveling northeast cannot enter the freeway traveling southeast unless they travel completely through the interchange and make a U-turn. Similarly, drivers traveling northwest cannot access the route to the southwest without taking a circuitous path and backtracking.

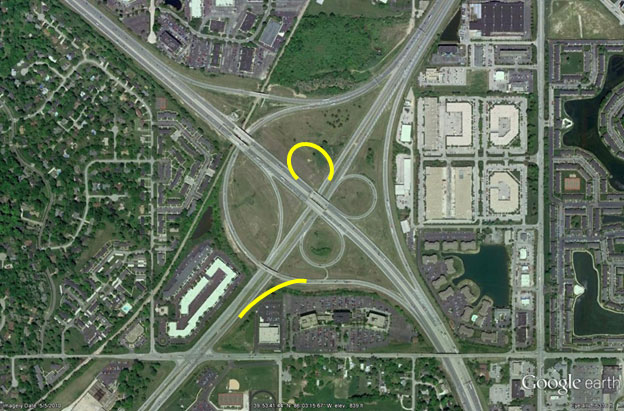
©2010 Google Earth^®
Figure 38. Photo. Example of missing movements.⁽⁴⁵⁾

After entering details of interchange-level site characteristics, the user enters ramp-specific characteristics for each ramp in the interchange in the order that a driver would encounter them while driving through the interchange. The user describes each ramp as an entrance or exit ramp, enters the origin or destination of the ramp and the type of ramp, and notes whether the ramp is part of a cloverleaf arrangement.

After entering general characteristics of each ramp, the user enters a series of counts, measurements, and other variables for each ramp. The information for these ramp-specific characteristics can come from plan sheets, in-person field visits, or (as was done in this study) aerial images from Google Earth^® or a similar online mapping service. There are 34 ramp-specific characteristics divided into three groups: lanes, exit ramp characteristics, and entrance ramp characteristics. The full list of characteristics for each ramp is shown in table 16. Many of the characteristics in the table are directly measured or observed (e.g., those with units in ft or those that are count variables). Remaining characteristics are based on the user choosing a value (i.e., yes or no). Inputs are formatted in this manner to help remove much of the subjectivity in evaluating an interchange of this type; the inputs require specific answers or numbers and largely eliminate the need for the user to make a determination of the complexity of an individual characteristic.

Table 16. Ramp-specific characteristics for spreadsheet tool.

Group/Characteristic	Unit
Lanes Measured at the Terminus of the Speed Change Lane (SCL)
Number of general purpose lanes at the start of the ramp	Count
Number of general purpose lanes at the ramp gore	Count
Number of managed lanes	Count
If managed lane is present, what is the separation device? (concrete barrier, candlestick, or paint)	Discrete choice
Left shoulder width (ft)	ft
Is there a concrete barrier at the edge of the left shoulder? (yes/no)	Discrete choice
Right shoulder width (ft)	ft
Is there a concrete barrier at the edge of the right shoulder? (yes/no)	Discrete choice
Number of concurrent routes on the main lanes	Count
Is visual clutter present (e.g., sight distance restricted by overhead bridges, buildings greater than three stories within 30 ft of travel way, etc.) (yes/no)?	Discrete choice
Exit Ramp Characteristics
Number of exiting lanes	Count
Left exit? (yes/no)	Discrete choice
Number of optional/shared exit lanes	Count
Number of exit only lanes	Count
At this location, is driver expectancy violated because a driver on a main lane has to change lanes to stay on the freeway? (yes/no)	Discrete choice
SCL type (parallel/taper)	Discrete choice
Alignment of ramp proper (loop/curve/straight)	Discrete choice
At this location, is driver expectancy violated because the main lanes are curving away from a straight ramp? (yes/no)	Discrete choice
At this location, is driver expectancy violated because a horizontal curve on the main lanes is so severe that aligning arrows on signs would be difficult? (yes/no)	Discrete choice
Multiple destinations from exit? (yes/no) (includes C-D roads)	Discrete choice
Distance from upstream ramp of interest (ft measured between painted gore points)	ft
Upstream ramp type (entrance/exit)	Discrete choice
Upstream ramp side (left/right)	Discrete choice
If upstream ramp is the entrance, is the auxiliary lane present? (yes/no/not applicable)	Discrete choice
Distance to downstream ramp (ft measured between painted gore points)	ft
Downstream ramp type (entrance/exit)	Discrete choice
Downstream ramp side (left/right)	Discrete choice
Entrance Ramp Characteristics
Number of entering lanes	Count
Left entrance? (yes/no)	Discrete choice
Entrance lane type (typical/auxiliary/through)	Discrete choice
SCL type (parallel/taper)	Discrete choice
Distance to downstream ramp (ft measured between painted gore points)	ft
Downstream ramp type (entrance/exit)	Discrete choice
Downstream ramp side (left/right)	Discrete choice

Factors, Threshold Values, and Points

After all user inputs are complete, the spreadsheet processes that information based on a set of factors, threshold values, and weights. Factors are those variables that the research team included based on the previous versions of the spreadsheet and the feedback from practitioners. Each factor has high and low threshold values for scoring. The weights are numerical values that assign relative importance to each factor, which are also based on the judgment of the research team supported by review of the previous spreadsheet. The factors, their threshold values, and points assigned based on the threshold value are shown in table 17 for those factors with yes/no answers and table 18 for those factors with numeric values.

Each factor was assigned a high and low threshold value on which to base the complexity impact of that variable. Values above the high threshold were assigned 10 points, values equal to or below the low threshold were zero points, and moderate values (between the high and low thresholds) were given 5 points. For example, if an approach had two concurrent routes through the entire length of the study corridor, the value for that factor was equal to the upper threshold value of 2, so the approach received 5 points for that factor. If the number of concurrent routes was three, then the approach received 10 points. In a similar manner, the value of each factor for each approach was tabulated, and a corresponding point value was assigned in the spreadsheet.

The minimum distance for calculating percentage of auxiliary lane length is 2,000 ft based on figure 10-68 from the 2011 AASHTO Green Book.⁽²⁾ Additionally, the minimum distance between entrance ramps is 1,000 ft.⁽²⁾ The distance between successive exit ramps (800 ft) and the weaving section length (0.5 mi) were based on engineering judgment, and the minimum widths of left (4 ft) and right (10 ft) shoulders were based on the Green Book.⁽²⁾

Table 17. Factors (questions) and threshold values used in the spreadsheet.

Label	Factor (In Order of How Information is Added to Spreadsheet)	10 Points (Answer is Yes)	Zero Points (Answer is No)
N	Is left shoulder less than minimum width of 4 ft?	Yes	No
O	Is there a concrete barrier less than minimum width distance of 4 ft to the left of the travel way?	Yes	No
P	Is right shoulder less than minimum width of 10 ft?	Yes	No
Q	Is there a concrete barrier less than minimum width distance of 10 ft to the right of the travel way?	Yes	No
R	Is a loop present on exit ramp?	Yes	No
S	Is a taper SCL present on exit ramp?	Yes	No
T	Is a taper SCL present on entrance ramp?	Yes	No
U	Is the number of general purpose lanes greater than three?	Yes	No
V	Are managed lanes present?	Yes	No
W	Is lane continuity violated?	Yes	No
X	Is there a claustrophobic feeling (e.g., buildings close to freeway)?	Yes	No
Y	Is the ramp straight while the main lanes are curved?	Yes	No
Z	Are the approaching main lanes curved?	Yes	No
AA	Is there an entrance ramp within minimum distance of 1,000 ft downstream of this entrance?	Yes	No
BB	Is there an exit ramp within minimum distance of 800 ft downstream of this exit?	Yes	No
CC	Is there < 0.5-mi weaving section between the entrance and the downstream left exit?	Yes	No
DD	Is there an entrance ramp followed closely by an exit, and is the auxiliary lane missing based on dimensions shown in the 2011 AASHTO Green Book?(2)	Yes	No
EE	Is the number of exit lanes equal to or greater than the number of through lanes?	Yes	No
FF	Is the number of entrance lanes equal to or greater than the number of through lanes?	Yes	No

The threshold values for each factor were assigned based on the research team's engineering judgment, reviewer feedback, and available research. For example, it was surmised that an approach with two concurrent routes was not particularly unusual and would not be especially taxing on the driver's mental workload; however, approaches with more than two routes would be more complex and should be scored accordingly. Similarly, the number of levels in an interchange is always at least two. The presence of an interchange is itself an indication of some complexity but not overly so. Therefore, an interchange having two levels has a moderate score of 5 points, while interchanges with three or more levels are assigned a high complexity score of 10 points.

Table 18. Factors (numeric) and threshold values used in the spreadsheet.

Label	Factor (In Order of How Information is Added to Spreadsheet)	10 points (When Value of the Factor > Value Below*)	Zero points (When Value of the Factor ≤ Value Below*)
A	Number of concurrent routes	2.0	1.0
B	Number of levels	2.0	1.0
C	Number of missing movements	2.0	0.99
D	Exit ramps per mile	1.0	0.5
E	Entrance ramps per mile	1.0	0.5
F	Left exits per mile	0.3	0
G	Left entrances per mile	0.3	0
H	Number of exit ramps with multiple destinations per mile	0.3	0
I	Multilane exit ramps per mile	0.3	0
J	Optional/shared exit lanes per mile	0.3	0
K	Exit only lanes per mile	0.3	0
L	Proportion of ramps where lane balance is not satisfied	0 percent	0 percent
M	How much shorter than minimum distance is the shortest auxiliary lane (as a percentage of minimum distance)?	0 percent	0 percent

*A total of 5 points are assigned when the value is equal to or less than the value listed in the 10-point column and greater than the value listed in the zero-point column.

Weights

After point values were calculated, weights were applied in the spreadsheet using the weight values shown in table 19. The 32 factors in table 19 have been rearranged from table 17 and table 18 so that they are presented in descending order of weight. Point values given to each factor for each approach were multiplied by the weight. Continuing the previous example, the moderate score of 5 points for concurrent routes was multiplied by the corresponding weight of 3, resulting in a weighted score of 15 points for concurrent routes on that approach.

Researchers tried a variety of weights to evaluate each factor and develop scores in the spreadsheet that would realistically reflect the characteristics of the sites and the ranking of the sites as estimated by the research team. Like the point values, the weights were also assigned based on the research team's estimation of the relative complexity of each factor supported by the feedback from practitioner reviewers. The values of the weights were also designed to sum to 100 so that a weight could easily be identified as a percentage of the total. With those parameters in place, the research team had a great deal of flexibility to determine how to account for those factors in the eventual complexity score.

Researchers used the weights to provide a measure of the complexity of a given factor relative to other factors. Factors with higher weights were deemed to have a greater impact on complexity than those with lower weights. Table 19 shows that the 32 factors used in the spreadsheet were each given weights between 1 and 5. The factors with the largest weights were lane continuity violations and weaving sections less than 0.5 mi in length. These were considered to be the elements that would contribute the most to driver workload and perceived complexity. The factors with the smallest weights were density of optional/shared exit lanes, presence of auxiliary lanes less than 2,000 ft in length, and number of entrance lanes greater than or equal to the number of through lanes. These were considered to be the least complex of the factors under consideration but still worthy of inclusion in the calculation of a complexity score. A review of table 19 shows that there were an additional 14 factors with a weight of 4, 5 factors with a weight of 3, and 8 factors with a weight of 2. The fact that half of the factors had weights of 4 or 5 is a reflection of the researchers' agreement with reviewers that these factors play a sizeable role in increasing the complexity of an interchange. The assignment of a weight of 1 or 2 does not mean that a factor is not complex but rather that it is not as complex as other factors in the judgment of the research team.

Factors with higher weights are generally concerned with ramp densities, left-side ramps, ramps with multiple destinations, lane balance violations, speed-change lanes with taper designs, more demanding alignments (e.g., loop ramps, curved approaches to ramps, etc.), and a perception of a claustrophobic effect due to large buildings or other items close to the freeway. In the estimation of the research team, these items are more complex and add more to the driver's mental workload than other items. In some cases, a factor was given less weight because researchers believed that another factor also at least partially accounted for its complexity, such as giving a left shoulder less than minimum width a weight of only 2 because the presence of a concrete barrier less than minimum width distance to the left of the travel way was considered to be worth a weight of 4. The location of the concrete barrier is related to the width of the shoulder, but the presence of a barrier increases complexity further because the driver is more concerned about a roadway departure if there is a concrete barrier nearby than if the median is more forgiving.

A factor that is not directly addressed in table 19 is the presence of a C-D road. The way that the spreadsheet treats a C-D road is that it simplifies the operation of the through route on the freeway because the number of access points is reduced. However, when considering the path that an exiting or entering driver must take, it could be argued that a C-D road increases complexity because those drivers have to navigate through at least one additional decision point to reach their destinations. A full exploration of the complexity effects of C-D roads was ultimately beyond the scope of this project, but it is definitely worthy of consideration as a future research topic.

Table 19. Factors and weights used in spreadsheet sorted by weight.

Order	Factors	Weight
W	Is lane continuity violated? (yes/no)	5
CC	Is there < 0.5-mi weaving section between entrance and downstream left exit? (yes/no)	5
Z	Are the approaching main lanes curved? (yes/no)	4
E	Entrance ramps per mile.	4
R	Is a loop present on exit ramp? (yes/no)	4
T	Is a taper SCL present on entrance ramp? (yes/no)	4
S	Is a taper SCL present on exit ramp? (yes/no)	4
U	Is the number of general purpose lanes greater than three? (yes/no)	4
X	Is there a claustrophobic feeling (e.g., buildings close to freeway)? (yes/no)	4
O	Is there a concrete barrier less than minimum width distance of 4 ft to the left of the travel way? (yes/no)	4
AA	Is there an entrance ramp within a minimum distance of 1,000 ft downstream of this entrance? (yes/no)	4
BB	Is there an exit ramp within a minimum distance of 800 ft downstream of this exit? (yes/no)	4
G	Left entrances per mile	4
F	Left exits per mile	4
H	Number of exit ramps w/multiple destinations per mile	4
L	Proportion of ramps where lane balance is not satisfied	4
DD	Is there an entrance ramp followed closely by an exit, and is the auxiliary lane missing based on dimensions shown in the 2011 AASHTO Green Book?(2)	3
Y	Is the ramp straight while the main lanes are curved? (yes/no)	3
Q	Is there a concrete barrier less than minimum width distance of 10 ft to the right of the travel way? (yes/no)	3
A	Number of concurrent routes	3
C	Number of missing movements	3
K	Exit only lanes per mile	2
V	Are managed lanes present? (yes/no)	2
D	Exit ramps per mile	2
N	Is the left shoulder less than the minimum width of 4 ft? (yes/no)	2
P	Is the right shoulder less than the minimum width of 10 ft? (yes/no)	2
EE	Is the number of exit lanes equal to or greater than the number of through lanes? (yes/no)	2
I	Multilane exit ramps per mile	2
B	Number of levels	2
M	How much shorter than minimum distance is the shortest auxiliary lane (as a percentage of minimum distance) ?	1
FF	Is the number of entrance lanes equal to or greater than the number of through lanes? (yes/no)	1
J	Optional/shared exit lanes per mile	1

Many of the factors considered in the spreadsheet are discrete choices, and the high threshold value is a reflection that the characteristic, if present on an approach, has a high impact on complexity for that approach. For other factors, the threshold is based on a measurement or a count, and there are values for which the factor may not have a substantial effect on complexity even if it is present at the site. These factors have some flexibility in adjusting the thresholds, if desired, to revise the base points assigned to values of those factors.

Adjusting Weights and Calculating Scores

The base points for each factor are multiplied by their respective weights to produce weighted scores, which are summed to produce a score for the entire approach. Approach scores are averaged to produce the interchange score. Given the limited number of factors with adjustable thresholds, researchers focused on the values of the weights to produce a set of interchange scores that best reflected the relative complexity of the study sites. Researchers tried a variety of weights for the 32 factors. The values shown in table 19 produced results most similar to the research team's qualitative evaluation of the sites, indicating that for these characteristics, weights, and threshold values, the results produced a generally accurate sense of the relative complexity of the interchanges studied. The researchers recognize that other practitioners and spreadsheet users could develop a logical basis for adjusting the weights and thresholds to a different set of values than those shown here; however, they believe that the values used in the spreadsheet are also a valid and reasonable option, and the consistency in the relative scores and groupings supports that conclusion.

All of the weighted factor scores are summed in the spreadsheet to produce a complexity score for the approach. The approach complexity scores are then averaged to produce an overall complexity score for the interchange, ranging between 10 and 1,000 points.

RESULTS

Scores

After all of the site information was entered into the spreadsheet and the weights were optimized, researchers tabulated the scores from all 28 study sites.

Table 20 shows the final scores for each study site. Sites are listed in order of descending complexity based on the judgment of the research team. Cells shaded in gray have spreadsheet scores that are different from their place on the list. A review of the list indicates that the spreadsheet generated scores that were generally consistent with researchers' estimation of the sites' relative complexity. There are two exceptions to the correlation between the scores and the researchers' estimated complexity, both of which are within one ranking of being correlated with the spreadsheet scores.

Table 20. Complexity scores for study sites.

Rank	Site	Interchange Complexity Score	Group
1	OH-2	590.00	1
2	VA-2	571.25	1
3	OH-3	568.75	1
4	AZ-2	466.25	1
5	AZ-1	422.50	1
6	OH-1	398.33	2
7	DE-3	390.00	2
8	OR-1	385.00	2
9	DE-2	373.75	2
10	GA-2	342.50	2
11	VA-1	338.75	2
12	OR-2	321.67	2
13	VA-3	307.50	2
14	NY-3	312.50	2
15	GA-3	291.25	3
16	IA-1	277.50	3
17	MD-1	275.00	3
18	IN-1	266.25	3
19	NY-1	260.00	3
20	SC-2	252.50	3
21	IN-3	256.25	3
22	DE-1	240.00	3
23	IA-2	238.75	3
24	GA-4	231.67	3
25	SC-1	215.00	4
26	AZ-3	215.00	4
27	IA-3	197.50	4
28	SC-3	180.00	4

Note: Gray shading indicates cells have spreadsheet scores that are different from their place on the list.

The sites in table 20 were divided into four distinct groups based on the spreadsheet scores. Sites with similar scores were viewed as having similar levels of complexity. The sites in group 1, the five sites with the highest scores, all had a complexity that was estimated to be much greater than that of the other 23 sites. In fact, the three highest scoring sites had substantially higher scores than the remaining sites, separated from sites 4 and 5 by more than 100 points. Group 2 represented sites that scored between 300 and 400, group 3 represented sites that scored between 230 and 300, and group 4 represented sites with scores below 230. A review of the two exception sites shows that despite their placement on the list, they were still contiguous to the group that contained the sites with similar scores; for example, NY-3 was one place lower in its ranking than its score would suggest, but researchers still considered it to be more complex than any of the group 3 sites. The similarity between exception scores and adjacent scores suggests that the differences in complexity between sites in the same group may not have been particularly significant. This characteristic is discussed in greater detail later in this chapter, but it should be emphasized that the ranking was based on the opinion of the researchers, as were the weights and scores associated with the spreadsheet calculations.

Interpretation of Scores

As mentioned previously, there was a noticeable gap between the highest scores and the remaining scores. In particular, three sites received scores over 550: OH-2, VA-2, and OH-3. These three sites were in constrained urban environments, had unusual geometry, and had high ramp densities with multiple destinations (e.g., see figure 39). As a result, these interchanges received a non-zero score for almost every variable in the spreadsheet on at least one approach. All had at least one approach with a score of 660 or greater, and the EB and WB approaches at VA-2 had scores of 720 and 770, respectively, which were the two highest scores in the database.

There was a substantial drop in score between these interchanges and the fourth site on the list, AZ‑2, which also had some unusual geometry but was not as constrained as the first three sites. The fifth highest scoring site, AZ-1, had similarities to AZ-2 but was even less constrained on its speed change lanes and ramp spacing.

The site with the lowest score, SC-3, was submitted because of its closely spaced ramps on an interstate highway intersected with two numbered routes that existed as at-grade city streets (see figure 40). While the geometry of the interchange was unusual, the lower score was a result of the configuration of the ramps. The site had a C-D system that required only one exit and one entrance from the freeway. The NB approach received a score of only 115, which was the second lowest score of any approach in the database. One reason why the site had a low score was because the intersecting numbered routes were not freeways, and their complexity could not be measured in the same way as that of freeway routes. The city streets had traffic signals and other traffic control devices not found on freeways as well as substantially lower speeds, which arguably reduced the complexity of navigating those routes. Regardless if they were less complex, their characteristics prevented them from being directly compared to freeways within the spreadsheet, and thus those routes were not tabulated.

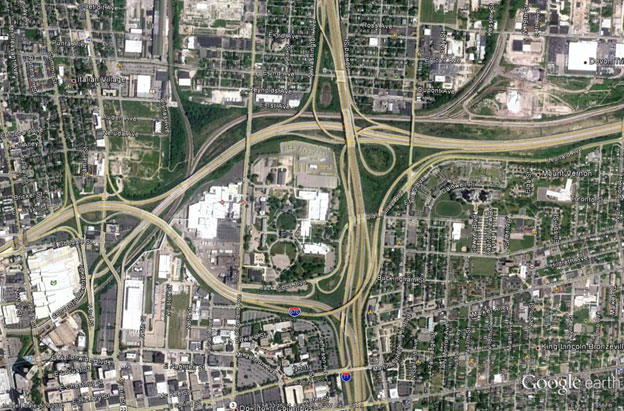
©2010 Google Earth^®
Figure 39. Photo. Configuration of site OH-2.⁽⁴⁶⁾

 

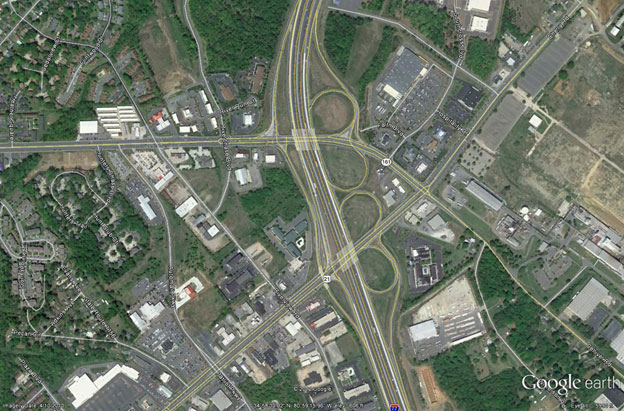
©2010 Google Earth^®
Figure 40. Photo. Configuration of site SC-3.⁽⁴⁷⁾

The other sites in group 4 typically had some unusual geometry in that at least one maneuver to travel from one route to another required using one or more ramps that were on an unusual alignment or were not constructed similar to the ramps for the other maneuvers at the interchange. However, the overall complexity of the interchanges was not nearly as great as the others in the study sites because drivers generally had to face few decision points, there were no left-side ramps, the number of general purpose lanes was low, there were no concurrent routes, and/or the ramp density was low.

Sites in groups 2 and 3 had complexity levels similar to other sites within the same group, reflecting a variety of combinations of ramp densities, left-side ramps, missing movements, travel lane configurations, lateral clearance and roadside environment, ramp geometry and alignment, and auxiliary lane configurations. Sites in group 2 had more characteristics that triggered points on their scores than sites in group 3. Overall, a comparison of sites in group 4 to sites in groups 3, 2, and 1 in table 20 shows sites that had increasingly more factors that contributed to an increased score. The combinations of those factors were not always the same, but the number of factors present at a site generally increased as the group changed from 4 to 1 so that sites in group 4 had few score-generating factors present, while group 1 sites had most (if not all) of those factors present on at least one approach.

DISCUSSION

This chapter described the development of the spreadsheet tool and provided the results of applying the spreadsheet to 28 existing interchanges across the United States. This concluding section discusses the ramifications of those results as well as key characteristics of the spreadsheet and its usefulness.

Features of the Spreadsheet

Key features of the spreadsheet tool include the following:

• The spreadsheet provides a means of objectively comparing the complexity of different interchanges based on a variety of geometric and other variables. It provides a numerical score that is directly comparable to scores from any other interchange. The basis of the spreadsheet is the characteristics of each ramp a driver encounters while driving through any corridor in the interchange.
• The spreadsheet accounts for differences between entrance ramps and exit ramps, frequency of ramps, differences between freeway-to-freeway connector ramps and service ramps, differences between taper and parallel speed-change lanes, presence of managed lanes, presence of narrow shoulders, number of concurrent routes and vertical levels, shared exit lanes, lane continuity and lane balance, and horizontal alignment, among other features.
• The spreadsheet is designed so that a user does not need to physically visit the interchange and take measurements in the roadway to complete it. All of the necessary information can be obtained through as-built plans or a mapping service such as Google Earth^®.
• The spreadsheet establishes threshold values for each factor to provide a means of assigning points that increase as the contributing characteristic increases in complexity. The spreadsheet also provides weights to each factor to generate higher scores for characteristics that are relatively more complex than others.
• The spreadsheet checks the distance between successive ramps based on the procedure defined in the 2011 AASHTO Green Book.⁽²⁾ This check allows the user to readily determine whether the distance between any two successive ramps is shorter than recommended, identifying a variable that contributes to complexity.
• The spreadsheet has a feature to account for the built environment adjacent to the freeway. A densely built urban environment adds more workload to a driver than a sparsely built rural environment. Similarly, the spreadsheet accounts for the number of lanes on both the ramps and on the general purpose lanes or main lanes. An increased number of lanes also means an increased number of decisions a driver must make to determine what lane is the correct lane for the driver's destination. More travel lanes also typically represent higher traffic volumes, resulting in more demands on a driver's attention while navigating the interchange.
• The spreadsheet accounts for each approach individually as well as collectively. This feature allows a user to identify a particularly complex approach within a high-scoring interchange.

Limitations of the Spreadsheet

Despite all of the features that can be found in the spreadsheet, there are a number of limitations. Some of these were included in discussions by the research team while developing the spreadsheet, while others were discovered during the review and quality control process. A summary of key limitations is as follows:

• By design, the spreadsheet includes only characteristics that can be obtained through Google Earth^® or a similar mapping service. This is intended to enable more practitioners to use the spreadsheet without requiring access to certain types of site-specific data, such as traffic volumes, construction history, or other information that may not be readily available.
• The spreadsheet does not directly account for a driver's destination or origin unless the driver is traveling straight through the interchange on the same route from approach to departure. While each exit and entrance ramp is included in the analysis, the spreadsheet does not directly document the series of decisions that an exiting or entering driver would have to make for all of the origin-destination combinations in a given interchange. Specifically, it does not estimate the complexity of a path from one route to another; it only describes complexity along the same route. For example, missing movements were not originally included in the spreadsheet, but consideration for them was added to help describe how some interchanges are more complex because of what is absent rather than what is present.
• The spreadsheet does not account for interactions between factors. Researchers discussed how one factor might affect another so that the combination of the two factors added more complexity than just the sum of the two factors individually. A proper exploration of interaction would be a very time consuming and complicated process and could not be adequately addressed in this study.
• While the spreadsheet does consider C-D roads within the variable for multiple destinations from a single ramp, it is unclear whether the full effect of C-D roads is truly addressed. C-D roads help to remove merging, diverging, and weaving maneuvers from the main lanes, thus helping to reduce complexity for through drivers. However, C-D roads may actually be more complex than traditional ramps because of the need to exit a substantial distance upstream of where a driver would expect to exit. That effect is not captured in the spreadsheet.
• Spreadsheet results do not fully appreciate the effect of adjacent interchanges. While the nearest upstream and downstream ramp is documented within the spreadsheet, the full effect of that ramp as part of another potentially complex interchange is not included in the analysis. Within the study sites compiled for this spreadsheet, there are three sets of interchanges that are either adjoining or in very close proximity. The two Oregon sites (OR-1 and OR-2) are a short distance apart, and both are constrained by the boundaries of the Willamette River. It is possible that the close proximity of the two interchanges makes traversing them more complex than if they were apart. Two Virginia sites (VA-1 and VA-2) are adjacent on I-395, and all three Delaware sites are close enough that a driver could easily drive through all three in one maneuver, changing routes only once. There could be a cumulative effect of these interchanges being so close together, but a thorough exploration of that effect is beyond the ability of this study.
• The spreadsheet is not designed to accommodate more than four approach legs. The spreadsheet was established to account for four corridors: NB, SB, EB, and WB. Those designations could change somewhat if the interchange in question is not particularly oriented to those directions, but the process for using the spreadsheet is the same if the interchange is quadrivial (i.e., having four roads meeting at a point). However, an arguably more complex interchange is one with more than four approaches (i.e., superquadrivial). The majority of sites submitted for New York are in this category. These interchanges are more complex than those evaluated because of the additional legs that must be considered. Unfortunately, expanding the spreadsheet to account for those additional legs would make for an unwieldy spreadsheet, and it is unclear whether a direct comparison between quadrivial and superquadrivial interchanges would be valid.
• As previously mentioned, the spreadsheet does not account for traffic volumes. An implied connection can be made between number of lanes and traffic volumes, but volumes are not directly requested in the set of input data. Similarly, the volume-to-capacity ratio or the level of service is not requested in the spreadsheet. Those variables could also have an effect on the complexity of an interchange, but they are not design characteristics and were deemphasized for this study.

Additional Considerations

In addition to the features and limitations of the spreadsheet, the following list includes some other items that may be considered when understanding how the spreadsheet functions:

• The topic of missing movements has been mentioned previously in this chapter where a missing movement prevents a driver on a given approach from directly accessing a different approach. It may be possible to go from one to the other but only through a series of maneuvers such as U-turns or multiple exits and entrances. Originally, missing movements were not included because the spreadsheet only evaluated existing ramps; the spreadsheet could not consider a ramp that did not exist. An adjustment was made to include missing movements.
• The results of the spreadsheet (i.e., the scores for each interchange and each individual approach) are dependent on the high/low threshold values and weights, which were subjectively determined by the research team with input from reviewers. Even the fact that the weights were originally designed to generate a 100-point total for ease of observation may affect the results, allowing for a different point total to provide a different means of establishing the weights. The research team believes that the 100-point total is beneficial and aids the user in understanding the results. Researchers also believe the sets of weights and threshold values presented are reasonable, given the consistency in the relative scores and groupings that resulted from the variety of combinations tested. The team also recognizes that a different set of weights and values that produce somewhat different scores could be developed on a reasonable basis.
• A full sensitivity analysis would help determine whether some weights or threshold values are inappropriately affecting the scores. A partial analysis was conducted on selected variables, but a full analysis was not possible in this study. For example, it is unclear whether the number of general purpose lanes is optimally accounted for in the spreadsheet. It is used as a surrogate for traffic volume and provides an indication of complexity if a driver must make additional lane changes, but it is unknown how sensitive the score is to the presence of two through lanes instead of three or four (if the threshold value was changed) and whether the presence of three general purpose lanes is truly as complex as the presence of a concrete barrier within 4 ft of the left side of the travel way. Again, the research team believes that the sets of weights and threshold values presented are reasonable, but the team also recognizes that a reasonable approach could produce a different set of weights and values that produce somewhat different scores.
• Another topic of consideration is how study distance is measured. This spreadsheet includes all the distance a driver must travel to navigate through the interchange, which means that the distance is measured from the point immediately downstream of the nearest ramp in the adjacent upstream interchange to the point of the nearest ramp for the succeeding interchange. This distance may be too large to sufficiently capture the effects of some calculated values, such as ramp density. The added distance may understate a ramp density's effects, particularly for cloverleaf interchanges that have segments of dense ramp locations (i.e., a cluster of ramps) followed by a long distance between ramps, resulting in a lower ramp density over the entire study distance.
• Operating speed and posted speed limit are not accounted for in this spreadsheet, and some of the sites had lower posted speed limits than others with similar or lower scores. For example, NY-3 had a posted limit of 45 mi/h on its major route; however, because of its ramp density and presence of left entrances and exits, it had a higher score than other sites with higher speed limits. It is unclear to what extent lower operating speeds would mitigate some of the complexity in an interchange such as NY-3 compared to other sites with fewer complex elements but higher speeds.
• The use of the average approach score to determine the overall interchange score may deemphasize a particularly complex approach. It is possible that the use of the highest approach score would be beneficial in determining the complexity of an interchange, but that method could also deemphasize a relatively simple approach. As stated before, practitioners could develop reasonable explanations for using either method.