Simulator Study of Signs for A Complex Interchange and Complex Interchange Spreadsheet Tool

PDF files can be viewed with the Acrobat® Reader®

APPENDIX B. COMPLEX INTERCHANGES SPREADSHEET TOOL

OVERVIEW

This appendix describes the spreadsheet tool developed as a method to evaluate and compare the complexity of freeway interchanges in the United States. It initially discusses the steps that led the research team to develop the spreadsheet in its current form and then provides a description of the spreadsheet itself and a review of the results obtained from the spreadsheet on existing sites. The concluding section examines what those results mean and how they can be interpreted.

INITIAL SPREADSHEET DEVELOPMENT

Team Discussions

Initially, the research team discussed a variety of methods to develop a format to apply a consistent set of criteria to measure complexity. Many potential variables were considered: geometric design variables, traffic control device variables, driver workload variables, etc. Researchers also discussed the basis on which the variables would be included as follows:

• Interchange-wide variables (e.g., number of levels).
• Route-specific variables (e.g., number of decision points/ramps to travel from an origin to a destination).
• Ramp-specific variables (e.g., left-side or multilane exit).

Finally, researchers discussed how the variables should be scored. That is, what quantity of a particular variable is considered to add complexity and how does that compare to the complexity of other variables? Individual variables could be assigned threshold values for complexity, and they could be weighted to reflect their complexity relative to other variables. The variables could also be compared to values in the 2011 AASHTO Green Book⁽²⁾.

Given all of these considerations, researchers compiled a list of noteworthy variables and assigned proposed values and weights to them to present to practitioners to obtain their feedback on the usefulness and meaningfulness of the initial version of the spreadsheet tool. The worksheet included 26 variables divided into the following three categories:

• Roadway geometry variables are as follows:
  • Number of concurrent routes.
  • Number of levels.
  • Exit ramps per mile.
  • Entrance ramps per mile.
  • Left exits per mile.
  • Left entrances per mile.
  • Exit ramps with multiple destinations per mile.
  • Multilane exit ramps per mile.
  • Optional/shared exit lanes per mile.
  • Exit only lanes per mile.
  • Lane balance condition.
  • Auxiliary lane as percent of minimum distance (in ft).
  
  
• Driver workload challenges are as follows:
  • Is the left shoulder less than the minimum width?
  • Is the right shoulder less than the minimum width?
  • Is there a loop on the exit ramp?
  • Is there a taper speed-change lane on the exit ramp?
  • Is there a taper speed-change lane on the entrance ramp?
  • Is the number of general purpose lanes greater than four?
  
  
• Driver expectancy violations are as follows:
  • Is the ramp straight while the main lanes are curved?
  • Are the approaching main lanes curved (resulting in difficulties in aligning arrows on signs)?
  • Is there an entrance within minimum distance downstream of this entrance?
  • Is there a short (less than 0.5 mi) weaving section between the entrance and the downstream left exit?
  • Is an entrance ramp followed closely by an exit, and is the auxiliary lane missing? (Based on Green Book figure 10-68.)⁽²⁾
  • Are there more exit lanes than through lanes?
  • Are there more entrance lanes than through lanes?
  • What is the number of missing legs?

Expert Panel Discussion

In January 2011, TTI conducted an expert panel discussion. Researchers wanted the panel to help identify factors that contribute to the driving complexity of an interchange area and to give their opinion on lists of variables already identified during the research as contributing to complexity. This discussion was limited to design and geometric variables and did not address existing signing or other traffic control devices currently installed at the interchanges. In addition to the four members of the TTI research team, the panel was also composed of six practitioners: three from State transportation, two from FHWA, and one from a State turnpike authority.

Researchers showed three examples of interchanges that some may deem complex, and they asked panelists to give their impressions of which interchange was the most complex. The panelists then reviewed the 26 variables, which the researchers presented with explanations behind their reasoning.

Overall, the panel thought the three categories of variables were a good fit for addressing interchange complexity, but they noted that the workload and expectancy categories were related (e.g., when driver expectancy is violated, it increases the workload for the driver and increases the amount of signing needed).

It was further suggested that workload is primarily driven by the density of decisions that a driver must make within an interchange area. In this case, the example stated was that if the decision points for several major destinations were within the interchange area, the workload would be significantly increased. Panelists stated that workload can be reduced through interchange design by spreading the decision points along the corridor and that addressing variables within the design category could eliminate complexity from both workload and expectancy violations. This point emphasizes the need for early coordination of geometric design and signing needs.

Prior to presenting the list of variables to the panel, researchers discussed how to assess the complexity of each of the 26 items listed and how to meaningfully and objectively compare the effects of each variable to the others on the list. Researchers discussed this issue with the panelists, along with some initial ideas on how to accomplish that comparison. The panelists echoed that sentiment and provided their comments and recommendations on how to assess each variable individually and comparatively in a revision of the list.

The panelists offered their suggestions on which variables were important and what their relative weights and scores should be, and they discussed which variables should be added or removed from the initial list of 26 characteristics. Based on the feedback, researchers revised the spreadsheet into its current version.

DEPARTMENT OF TRANSPORTATION SITES

To determine how well the spreadsheet tool would evaluate interchanges, the research team issued a request to State transportation departments to send the team the locations of the most complex interchanges in their respective States. The research team received responses from 11 States, documenting 35 interchanges. The 11 States and number of reported interchanges include the following:

• Arizona: Three interchanges.
• Delaware: Three interchanges.
• Georgia: Four interchanges.
• Indiana: Three interchanges.
• Iowa: Three interchanges.
• Maryland: Two interchanges.
• New York: Six interchanges.
• Ohio: Three interchanges.
• Oregon: Two interchanges.
• South Carolina: Three interchanges.
• Virginia: Three interchanges.

A 12th State, Wyoming, did respond to the request for information but stated that it did not have any interchanges that its transportation department classified as complex.

After reviewing the information provided by the State transportation departments, the research team used 28 of the interchanges for processing in the spreadsheet. Six of the remaining interchanges (one in Georgia, one in Maryland, and four in New York) contained more than four approaches (which is the capacity of the spreadsheet), while the last site (in Indiana) was not used because of poor image quality on both the aerial and street view pictures available in the Google Earth^® mapping service database due to construction at the time the images were recorded. The locations of the study sites are summarized in table 15. Those not used in the spreadsheet tool development are noted.

SPREADSHEET TOOL

In its current version, the spreadsheet focuses on the following characteristics:

• Three interchange-wide characteristics.
• A selection of cross section characteristics at the terminus of the speed-change lane of each ramp.
• Ramp-specific characteristics that are dependent on whether the ramp is an entrance ramp or an exit ramp.

A goal during spreadsheet development was to have a format that would be easy for practitioners to understand and use. The format is based on characteristics of each ramp in the interchange. The intent is to document the decision points, along with the associated pieces of information to be processed, that a through driver would encounter while driving on that route from one end of the interchange to the other. The spreadsheet is designed to accommodate up to four routes, which are labeled to correspond to the four cardinal compass directions: NB, southbound (SB), EB, and WB. This format allows users to enter the variables for each ramp that exists along any of the four routes, and the spreadsheet processes a series of calculations to convert those site characteristics into an interchange complexity score that can be compared to other interchanges.

After users enter all of the variables, the spreadsheet calculates a complexity score for each route and for the entire interchange. The maximum possible score for a route and for an interchange overall is 1,000 points. The theoretical minimum is zero points, but the practical minimum is 10 points, which is the score given to any interchange with two levels. The “User Inputs” section in this chapter describes the process of completing the spreadsheet with the revised set of characteristics.

Spreadsheet Development

Researchers entered the information on all 28 study sites into the spreadsheet tool, taking measurements and observations from Google Earth^® . While entering the information into the spreadsheet, researchers were also monitoring the performance of the spreadsheet, checking that each of the dozens of equations processing a particular site contained the proper operators and referenced the correct data. As the data were entered, researchers made changes to equations as needed to produce the correct results. Researchers also considered the scores that were generated as the information for each interchange was entered, to begin developing an appreciation of how well the spreadsheet identified the relative complexities of the study sites. Discussion of the complexity scores and their components is provided in more detail in the later sections of this appendix.

In addition, researchers reviewed the format and layout of the spreadsheet for its ability to receive data in a manner that would be intuitive and straightforward for the user. The research team decided to use color shading to indicate the purpose of a cell. In general, the areas shaded green are those that are intended for the user to enter values, the areas in white are calculations and equations, and black or gray cells provide visual boundaries on the screen. White, black, and gray cells need no input, and the user should skip those cells when entering data. This color scheme format is intended to help the user focus on the areas that require input (e.g., site characteristics) and avoid cells that do not need input and may even cause errors in the spreadsheet if changed (e.g., built-in equations).

User Inputs

To use the spreadsheet, a user must enter a series of values into the appropriate cells for each ramp on each approach. Cells in the spreadsheet that receive user input are shaded green to differentiate them from white cells containing labels and equations and black or gray cells that provide visual boundaries between sections of the spreadsheet. A set of step-by-step instructions is provided in one tab of the spreadsheet; those instructions are summarized in the following section of this appendix.

To begin, users enter basic descriptive information about the interchange. Figure 73 shows this area of the spreadsheet. Users first enter the city where the interchange is located, and then they enter the primary and secondary routes of the interchange (see column Q). Next, users enter the length of the study corridor in each direction measured from the beginning of the most upstream ramp of the interchange to the end of the most downstream ramp; this information is entered in columns J through M. Finally, users enter the number of vertical levels in the interchange and the number of missing movements for each direction, also in columns J through M. A missing movement is defined as the condition in which a direct path from one approach to another does not exist. Examples of missing movements are shown by the yellow lines in figure 38. Drivers traveling northeast cannot enter the freeway traveling southeast unless they travel completely through the interchange and make a U-turn. Similarly, drivers traveling northwest cannot access the route to the southwest without taking a circuitous path and backtracking.

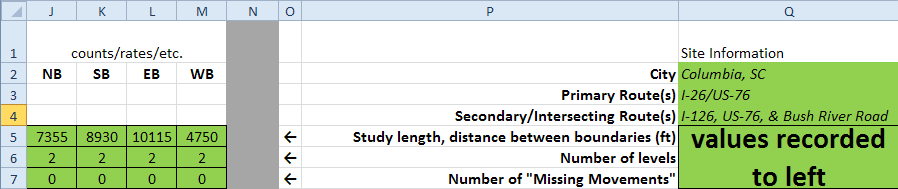
Figure 73. Screenshot. Portion of spreadsheet containing interchange information.

After entering details on the interchange-level site characteristics, the users enter ramp-specific characteristics for each ramp in the interchange. Within the spreadsheet, ramps are numbered in the order that a driver would encounter them while driving through the interchange, as shown in columns R through U in figure 74. Each ramp is described as an entrance or exit ramp. Additionally, the origin or destination of the ramp and the type of ramp are recorded, and it is noted whether the ramp is part of a cloverleaf arrangement.

After entering general characteristics of each ramp, users enter a series of counts, measurements, and other variables for each ramp. The information for these ramp-specific characteristics can come from plan sheets, in-person field visits, or (as was done in this study) aerial images from Google Earth^® or a similar online mapping service. There are 34 ramp-specific characteristics divided into three groups: lanes, exit ramp characteristics, and entrance ramp characteristics. The full list of characteristics for each ramp is shown in table 16.

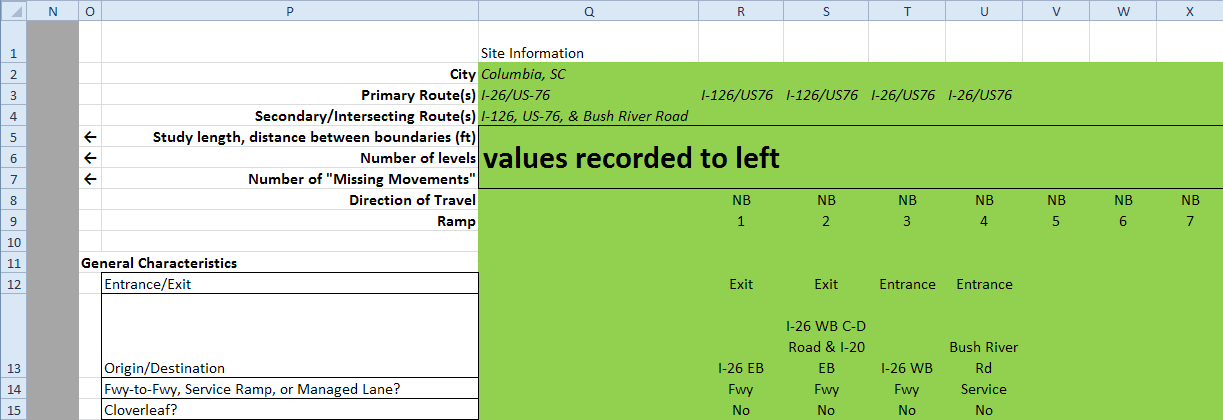
Figure 74. Screenshot. Portion of spreadsheet containing ramp description.

Many of the characteristics in table 16 are directly measured or observed (e.g., those with units of feet or those that are count variables). Remaining characteristics are entered based on users choosing one of a predetermined set of possible values (i.e., yes or no). Some of these choice variables may also involve a measurement, but the actual input is based on a binary (or sometimes trinary) decision. These inputs are formatted in this manner to help remove much of the subjectivity that could be involved in evaluating an interchange of this type; the inputs require specific answers or numbers and largely eliminate the need for the user to make a determination of the complexity of an individual characteristic. There are three exceptions to this: the visual clutter variable in the lane group and the two characteristics on curves approaching an exit ramp. These exceptions require some judgment on the part of the user, but making that determination could be done through a review of a photolog of the roadside area or a mapping service such as the street-view feature in Google Earth^® .

Spreadsheet users enter the values of the lane characteristics for the first ramp in the NB direction, and then, depending on whether the ramp is an entrance ramp or an exit ramp, they enter the values for the appropriate group of ramp characteristics. This process is then repeated for each remaining ramp in the NB direction followed by ramps in the SB, EB, and WB directions. In the event that a particular approach does not exist (e.g., the interchange has only three approach legs), the corresponding set of ramp inputs is omitted in the data entry process.

When the user inputs have all been entered, the spreadsheet performs four interim calculations to prepare the data for use in tabulating complexity scores, as shown in rows 54 through 58 in figure 75. The through lane-to-exit lane (or entrance lane) ratio is calculated to determine whether an excessive number of ramp lanes makes an interchange more complex, particularly if there are more ramp lanes than through lanes. The auxiliary lane length downstream of each entrance ramp is calculated to compare with criteria from the Green Book on appropriate lengths of auxiliary lanes.⁽²⁾ The lane balance calculation checks whether the number of lanes available downstream of the ramp is at least as great as the number of lanes upstream of the ramp. These items are discussed further in the “Factors, Threshold Values, and Points” section.

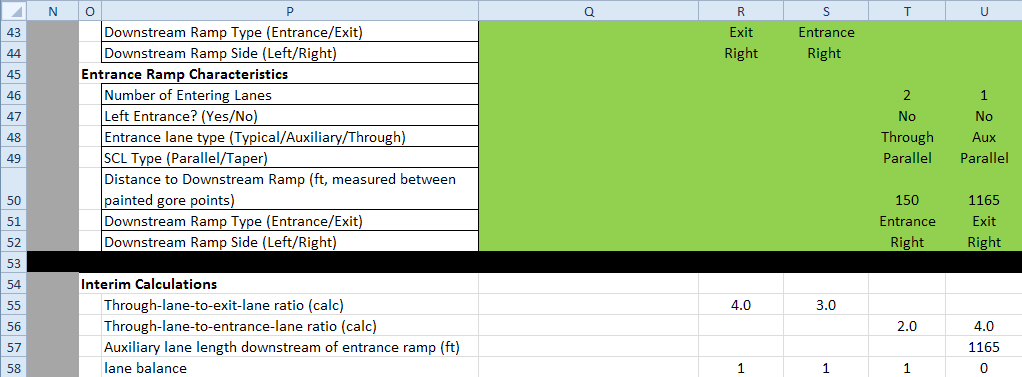
Figure 75. Screenshot. Portion of spreadsheet containing interim calculations.

Factors, Threshold Values, and Points

After all of the user inputs are stored in the spreadsheet and the interim calculations are completed, the spreadsheet processes that information based on a set of factors, threshold values, and weights. Factors include variables that the research team defined as important based on the previous versions of the spreadsheet and the feedback from practitioners. Each factor has high and low threshold values for scoring. The weights are numerical values that assign relative importance to each factor based on the judgment of the research team supported by a review of the previous spreadsheet. The factors, their threshold values, and points that would be assigned based on the threshold value are shown in table 17 for those factors with yes or no answers and table 18 for those factors with numeric values.

Each factor was assigned a high and low threshold value on which to base the impact of that variable on complexity for the given interchange. Values above the high threshold were assigned 10 points, values equal to or below the low threshold were zero points, and moderate values (between the high and low thresholds) were given 5 points. Using the example shown in figure 76, the NB approach has two concurrent routes (row 60) through the entire length of the study corridor (column J). The number of concurrent routes is equal to the upper threshold value of 2, so the NB approach receives 5 points (column F). The SB approach also has two concurrent routes and receives the same 5 points (columns K and G). The EB and WB approaches contain only one route, which is equal to the low threshold value; therefore, the EB and WB approaches receive zero points for this factor (columns L, M, H, and I). In a similar manner, the value of each factor was tabulated, and a corresponding point value was assigned in the spreadsheet.

The minimum distance for calculating percentage of auxiliary lane length is 2,000 ft, and the minimum distance between entrance ramps is 1,000 ft.⁽²⁾ The distance between successive exit ramps (800 ft) and the weaving section length (0.5 mi) were based on engineering judgment, and the minimum widths of left (4 ft) and right (10 ft) shoulders were based on the Green Book.⁽²⁾

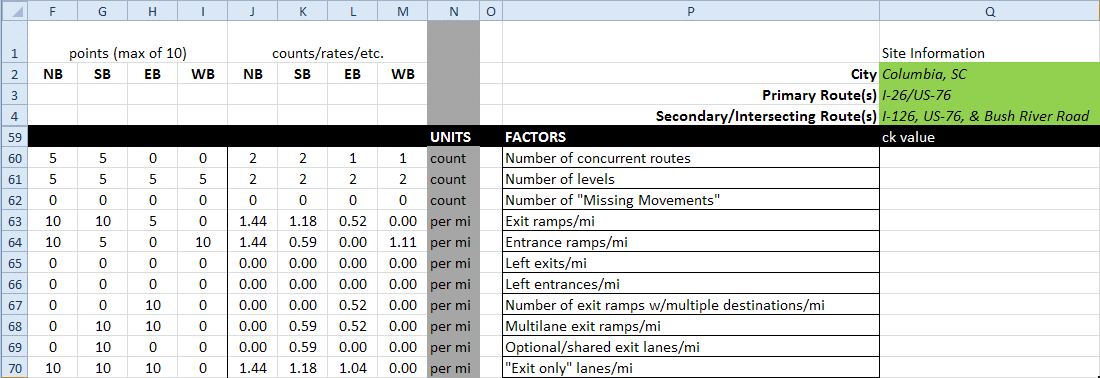
Figure 76. Screenshot. Example of factor scores.

The threshold values for each factor were assigned based on the research team’s engineering judgment, reviewer feedback, and available research. For example, it was surmised that an approach with two concurrent routes was not particularly unusual and would not be especially taxing on the driver’s mental workload; however, approaches with more than two routes would be more complex and should be scored higher accordingly. Similarly, the number of levels in an interchange is always at least two. The presence of an interchange is an indication of some complexity, but not overly so. Therefore, an interchange having two levels has a moderate score of 5 points, while interchanges with three or more levels are assigned a high complexity score of 10 points.

Weights

Once the point values were assigned, weights were applied in the spreadsheet using the values in table 19. The point values given to each factor for each approach were multiplied by the weight. Figure 77 shows a continuation of the example in figure 76. For the NB and SB approaches, the moderate score of 5 points for concurrent routes was multiplied by the corresponding weight of 3, resulting in a weighted score of 15 points (row 60, columns B and C). The zero-point scores for the EB and WB approaches were also multiplied by 3, producing weighted scores of zero points in columns D and E of row 60.

Similar to the point values, the weights were also assigned based on the research team’s estimation of the relative complexity of each factor, supported by the feedback from practitioner reviewers. The values of the weights were also designed to sum to 100 so that a weight could easily be identified as a percentage of the total.

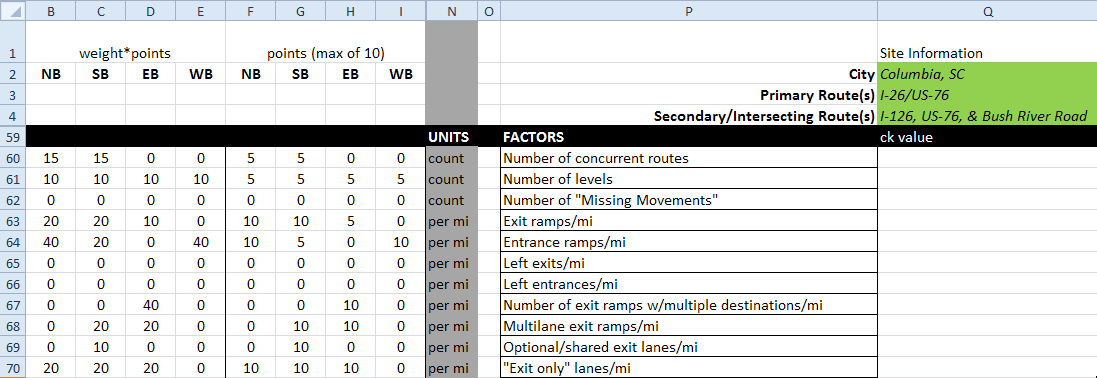
Figure 77. Screenshot. Example of weighted factor scores.

Researchers tried a variety of combinations of weights to evaluate each factor and develop scores in the spreadsheet that would realistically reflect the characteristics of the sites studied and the ranking of the sites as estimated by the research team. As mentioned previously, the goal was to develop a method of comparing the complexity of various interchanges based on an objective scale. Researchers determined that the numerical score used should have a base of 100 points. In addition, the list of factors shown in table 17 and table 18 were determined based on feedback from reviewers and practitioners as well as the researchers' own personal experience and professional judgment. With those parameters in place, the research team had a great deal of flexibility to determine how to account for those factors in the eventual complexity score. The 32 factors in table 19 have been rearranged from table 17 and table 18 so that they are presented in descending order of weight.

Researchers used the weights to provide a measure of the complexity of a given factor relative to other factors. Factors with higher weights were deemed to have a greater impact on complexity than those with lower weights. Table 19 shows that the 32 factors used in the spreadsheet were each given weights between 1 and 5. The factors with the largest weights were lane continuity violations and weaving sections less than 0.5 mi in length; these were considered to be the elements that would contribute the most to driver workload and perceived complexity. The factors with the smallest weights were density of optional/shared exit lanes, presence of auxiliary lanes less than 2,000 ft in length, and number of entrance lanes greater than or equal to the number of through lanes. These were considered to be the least complex of the factors under consideration but still worthy of inclusion in the calculation of a complexity score. A review of table 19 shows that there were an additional 14 factors with a weight of 4, 5 factors with a weight of 3, and 8 factors with a weight of 2. The fact that half of the factors had weights of 4 or 5 is a reflection of the researchers' agreement with reviewers that these factors play a sizeable role in increasing the complexity of an interchange. The assignment of a weight of 1 or 2 does not mean that a factor is not complex but rather that it is not as complex as other factors in the judgment of the research team.

The factors with higher weights are generally those concerned with ramp densities, left-side ramps, ramps with multiple destinations, lane balance violations, speed-change lanes with taper designs, more demanding alignments (e.g., loop ramps, curved approaches to ramps, etc.), and a perception of a claustrophobic effect due to large buildings or other items close to the freeway. In the estimation of the research team, these items are more complex and add more to the driver's mental workload than other items, such as the number of vertical levels in the interchange, the presence of adjacent managed lanes, or the number of concurrent routes on an approach. In some cases, a factor was given less weight because researchers believed that another factor also at least partially accounted for its complexity, such as giving a left shoulder less than minimum width a weight of only 2 because the presence of a concrete barrier less than minimum width distance to the left of the travel way was considered to be worth a weight of 4. The location of the concrete barrier is a reflection of the width of the shoulder, but the presence of a barrier increases complexity further because the driver is more concerned about a roadway departure if there is a concrete barrier nearby than if the roadside is more forgiving.

A factor that is not directly addressed in table 19 is the presence of a C-D road. The way that the spreadsheet treats a C-D road is that it simplifies the operation of the through route on the freeway because the number of access points is reduced. However, when considering the path that an exiting or entering driver must take, it could be argued that a C-D road increases complexity because those drivers have to navigate through at least one additional decision point to reach their destinations. A full exploration of the complexity effects of C-D roads is ultimately beyond the scope of this project, but it is definitely worthy of consideration as a potential research topic for a future project.

Each factor was given base points based on its threshold value. Table 17 and table 18 show the threshold values assigned to each factor to determine whether the characteristics of that factor had a high, moderate, or low effect on a specific site. Researchers set the threshold values based on their judgment of what constituted an amount that increased complexity. For example, researchers determined that an approach with only one route had a minimal impact on complexity, two concurrent routes would have a moderate effect, and more than two concurrent routes would have a high impact. Low-impact factors were given base points of zero, so even a factor that had a high weight would not affect the interchange's final score if that factor had a minimal presence.

Many of the factors considered in the spreadsheet are discrete choices, and the high threshold value is a reflection that the characteristic is present on an approach and has a high impact on complexity for that approach. For other factors, the threshold is based on a measurement or a count, and there are values for which the factor may not have a substantial effect on complexity even if it is present at the site. These factors have some flexibility in adjusting the thresholds, if desired, to revise the base points assigned to values of those factors.

Adjusting Weights

The base points for each factor are multiplied by their respective weights to produce weighted scores, which are summed to produce a score for the entire approach; approach scores are averaged to produce the interchange score. Given the limited number of factors with adjustable thresholds, researchers focused on the values of the weights to produce a set of interchange scores that best reflected the relative complexity of the study sites. Researchers tried a variety of combinations of weights for the 32 factors such as increasing some weights as high as 6 and balancing those increases with decreases in other factors to maintain the overall sum of 100. Each new set of weights produced different scores for each interchange. The values shown in table 19 produced similar results as the groupings of the study sites done by the research team, indicating that for the characteristics included in this spreadsheet and for the weights and threshold values shown in the table, the results produced a general sense of the relative complexity of the interchanges studied. The researchers recognize that other practitioners and spreadsheet users could develop a logical basis for adjusting the weights and thresholds to a different set of values than those shown in this appendix; however, researchers believe that the values used in the spreadsheet are also a valid and reasonable option, and the consistency in the relative scores and groupings supports that conclusion.

Calculating Scores

All of the weighted factor scores are summed in the spreadsheet to produce a complexity score for the approach. The approach complexity scores are then averaged to produce an overall complexity score for the interchange. An example of this scoring is shown in figure 78.

Figure 78. Screenshot. Example of approach and overall complexity scores.

The maximum possible score for an approach (and for an interchange overall) is 1,000 points. The theoretical minimum is zero points, although the practical minimum is 10 points because a two-level interchange will receive a weighted score of 10 points for this characteristic. In the example in figure 78, the interchange has an overall score of 215, which is a relatively low score, suggesting a low level of complexity. The overall score is the average of scores from the individual approaches, which ranged from a low of 50 to a high of 315 at this site. The primary route of this interchange was located on the north-south corridor, so it is reasonable that the more complex scores would appear on those approaches. The EB corridor also had some complex elements, but the WB approach had non-zero scores for only two factors: number of levels and entrance ramps per mile. As mentioned previously, the score for having two levels is inherent in every interchange, so the only additional complexity element in the interchange for the WB corridor was the presence of entrance ramps at a rate of greater than 1.0 per mile.

RESULTS

Scores

After all of the site information was entered into the spreadsheet and the weights were optimized, researchers tabulated the scores from all 28 study sites. Table 20 shows the scores for each study site generated by the final version of the spreadsheet. Sites are listed in order of descending complexity based on the judgment of the research team. Sites shaded gray have spreadsheet scores that are different from their place on the list. A review of the list indicates that the spreadsheet generated scores that were generally consistent with researchers' estimation of the sites' relative complexity. There are two exceptions to the correlation between the scores and the researchers' estimated complexity, both of which are within one ranking of being correlated with the spreadsheet scores.

The sites in table 20 were divided into four distinct groups based on the spreadsheet scores. Sites with similar scores were viewed as having similar levels of complexity. Group 1 was composed of the five sites with the highest scores, and all had complexity that was estimated to be much greater than that of the other 23 sites. In fact, the three highest-scoring sites had much higher scores than the remaining sites, separated from sites 4 and 5 by more than 100 points. Group 2 represented sites that scored between 300 and 400, group 3 was made up of sites between 230 and 300, and group 4 contained sites with sub-230 scores. A review of the two exception sites shows that despite their placement on the list, they were still contiguous to the group that contained the sites with similar scores. For example, NY-3 was one place lower in its ranking than its score would suggest, but researchers still considered it to be more complex than any of the group 3 sites. The similarity between exception scores and adjacent scores suggests that the differences in complexity between sites in the same group may not have been particularly significant. This characteristic will be discussed in greater detail later in this appendix, but it should be emphasized that the ranking was based on the opinion of the researchers, as were the weights and scores associated with the spreadsheet calculations. It is possible that a practitioner could logically rank some of the sites in table 20 differently or develop a set of weights and scores that correlates all 28 scores with their rankings. Further details on the two exception sites and on the rankings, weights, and scores in general are provided in the following sections.

Score Exceptions

The first exception site in table 20 is NY-3 (ranked 14th on the list), although its score was not considerably different than the site ranked above it. This site was an interchange with unusual geometry that utilized a series of exit only lanes and indirect paths to accommodate all of the possible movements from each approach. For all of the left-turn movements, it was necessary to travel through the interchange and make a U-turn to arrive at the desired destination. In addition, all of the ramps were on the left side of the travel way, so even right-turn maneuvers required entering or exiting the major route on the left. The geometry was also somewhat constrained, which produced high scores for exit ramp density, narrow shoulders, and a claustrophobic effect. The site with the next highest rank (VA-3) had a much larger footprint and had seven numbered routes on its four legs (including three interstate routes that terminated at the interchange) compared to the three routes at NY-3. The Virginia site also had some unique alignments for several of its access ramps, and it had higher posted speed limits (60 mi/h) than the New York site (45 or 35 mi/h), prompting researchers to give the Virginia site a higher rank.

The second exception site was SC-2, which had a score that was lower than its place on the list (ranked 20th). This site had two missing movements and some very unusual geometry that placed two interstate highways parallel to each other for a short distance (see figure 79). Because of this arrangement, the ramp densities were low, and there were no points added for concurrent routes. The interchange was arranged such that the ramps typically had ample speed-change lanes, so the scores for those characteristics were also low. However, particularly for unfamiliar drivers, traversing this interchange and determining the most appropriate path to take to arrive at a desired destination could be quite challenging. As a result, researchers elevated its place on the list in table 20.

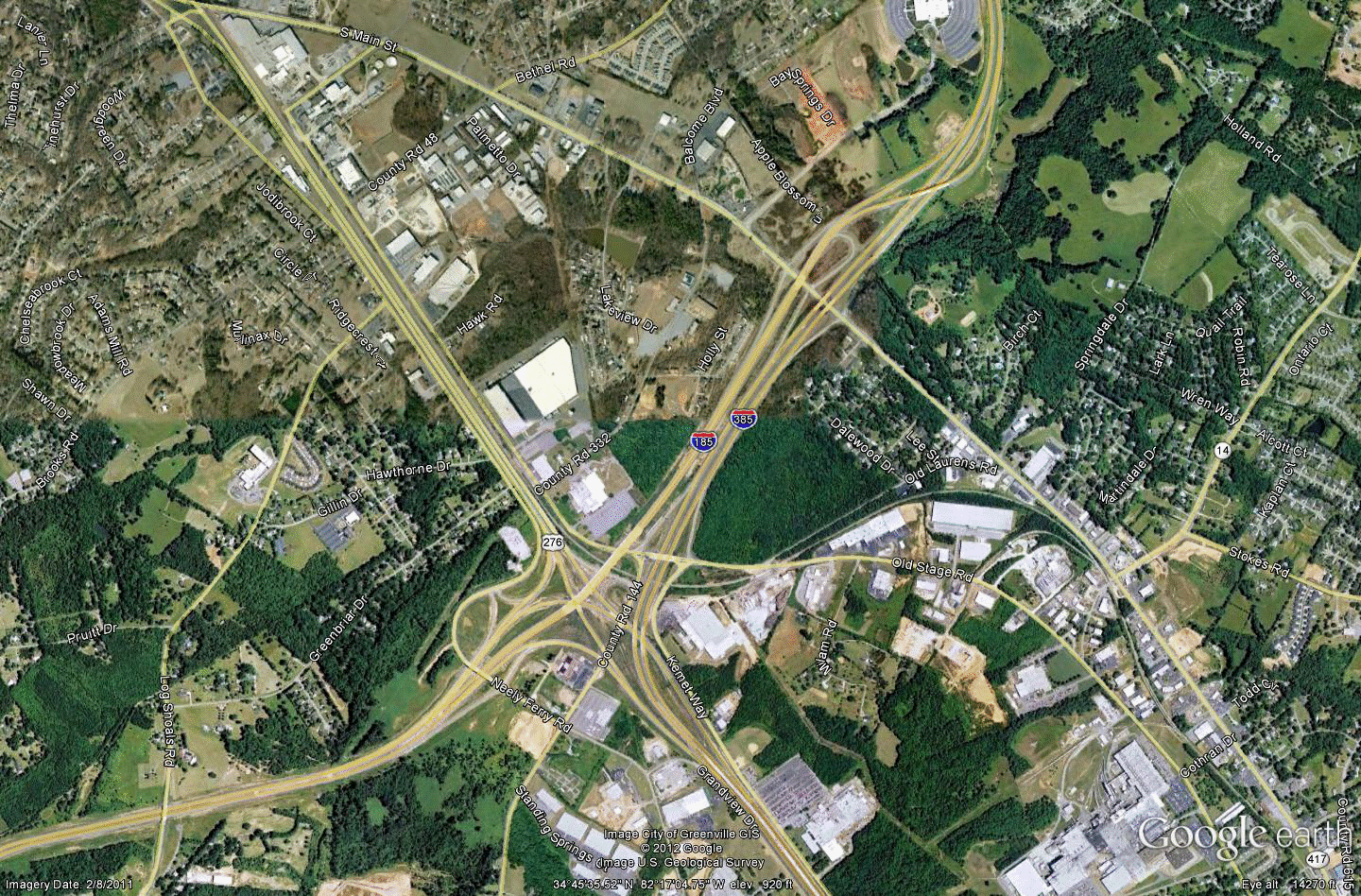
©2011 Google Earth^®
Figure 79. Photo. Configuration of site SC-2. ⁽⁴⁹⁾

Interpretation of Scores

As mentioned previously, there was a noticeable gap between the highest scores and the remaining scores. In particular, three sites received scores over 550: OH-2, VA-2, and OH-3. These three sites were in constrained urban environments, had unusual geometries, and had high ramp densities with multiple destinations (e.g., the aerial view of OH-2 in figure 39). As a result, these interchanges received a non-zero score for almost every variable in the spreadsheet on at least one approach. All had at least one approach with a score of 660 or greater, and the EB and WB approaches at VA-2 had scores of 720 and 770, respectively, which were the two highest scores in the database.

There was a substantial drop in score between these interchanges and the fourth site on the list, AZ-2. AZ-2 also had some unusual geometry, but it was not as constrained as the first three sites. The fifth highest-scoring site, AZ-1, had similarities to AZ-2 but was even less constrained on its speed-change lanes and ramp spacing.

The site with the lowest score, SC-3, was submitted because of its closely spaced ramps on an interstate highway intersected with two numbered routes that existed as at-grade city streets
(see figure 40). While the geometry of the interchange was unusual, the lower score was a result of the configuration of the ramps. The site had a C-D system that required only one exit and one entrance from the freeway. The NB approach received a score of only 115, which was the second-lowest score of any approach in the database. One important reason why the site had a low score was because the intersecting numbered routes were not freeways, and their complexity could not be measured in the same way as that of freeway routes. The city streets had traffic signals and other traffic control devices not found on freeways, as well as substantially lower speeds, which arguably reduced the complexity of navigating those routes. Regardless if they were less complex, their characteristics prevented them from being directly compared to freeways within the spreadsheet, and thus those routes were not tabulated.

It should also be noted that because the C-D road system removes entering and exiting traffic from the main lanes of the freeway with just one entrance and one exit, the effect of the ramp configuration on the complexity score was low. The research team discussed this effect, as well as effects on other C-D sites, to consider whether the presence of a C-D road actually increases or decreases complexity. This concept is discussed further in the explanation of weights and points section.

The other sites in group 4 typically had some unusual geometry in that at least one maneuver to travel from one route to another required using one or more ramps that were on an unusual alignment or were not constructed similar to the ramps for the other maneuvers at the interchange. However, the overall complexity of the interchanges was not nearly as great as the others in the study sites because drivers generally had to face few decision points, there were no left-side ramps, the number of general purpose lanes was low, there were no concurrent routes, and/or the ramp density was low.

Sites in groups 2 and 3 had complexity levels similar to other sites within the same group, reflecting a variety of combinations of ramp densities, left-side ramps, missing movements, travel lane configurations, lateral clearance and roadside environment, ramp geometry and alignment, and auxiliary lane configurations. Sites in group 2 had more characteristics that triggered points on their scores than sites in group 3. Overall, a comparison of sites in group 4 to sites in groups 1–3 in table 20 shows sites that had increasingly more factors that contributed to an increased score. The combinations of those factors were not always the same, but the number of factors present at a site generally increased as the group changed from 4 to 1, so that sites in group 4 had few score-generating factors present, while group 1 sites had most (if not all) of those factors present on at least one approach.

DISCUSSION

The previous sections in this appendix described the activities taken by the research team to develop the spreadsheet tool and provided the results of applying the spreadsheet to 28 existing interchanges across the United States. This concluding section discusses the ramifications of those results as well as key characteristics of the spreadsheet and its usefulness.

Features of the Spreadsheet

The following list provides a summary of the features of the spreadsheet tool:

• The spreadsheet provides a means of objectively comparing the complexity of different interchanges based on a variety of geometric and other variables. The spreadsheet provides a numerical score that is directly comparable to scores from any other interchange. The basis of the spreadsheet is the characteristics of each ramp a driver encounters while driving through any corridor in the interchange.


• The spreadsheet accounts for differences between entrance ramps and exit ramps, frequency of ramps, differences between freeway-to-freeway connector ramps and service ramps, differences between taper and parallel speed-change lanes, presence of managed lanes, presence of narrow shoulders, number of concurrent routes and vertical levels, shared exit lanes, lane continuity and lane balance, and horizontal alignment, among other features.


• The spreadsheet is designed so that a user can complete the spreadsheet from the office. There is no need to physically visit the interchange and take measurements in the roadway. All of the necessary information can be obtained through as-built plans or a mapping service such as Google GoogleEarth^® .


• The spreadsheet establishes threshold values for each factor to provide a means of assigning points that increase as the contributing characteristic increases in complexity. The spreadsheet also provides weights to each factor to generate higher scores for characteristics that are relatively more complex than others.


• The spreadsheet checks the distance between successive ramps based on the procedure defined in the 2011 AASHTO Green Book.⁽²⁾ This check allows the user to readily determine whether the distance between any two successive ramps is shorter than recommended, identifying a variable that contributes to complexity.


• The spreadsheet has a feature to account for the built environment adjacent to the freeway. A densely built urban environment adds more workload to a driver than a sparsely built rural environment. Similarly, the spreadsheet accounts for the number of lanes on both the ramps and on the general purpose lanes or main lanes. An increased number of lanes also means an increased number of decisions a driver must make to determine what lane is the correct lane for the driver’s destination. More travel lanes also typically represent higher traffic volumes, resulting in more demands on a driver’s attention while navigating the interchange.


• The spreadsheet accounts for each approach individually as well as collectively. This feature allows a user to identify a particularly complex approach within a high-scoring interchange.

Limitations of the Spreadsheet

Despite all of the features that can be found in the spreadsheet, there are a number of limitations as well. Some of these were included in discussions by the research team while developing the spreadsheet, while others were discovered during the review and quality control process. Key limitations include the following:

• By design, the spreadsheet includes only characteristics that can be obtained through Google Earth^® or a similar mapping service. This is intended to enable more practitioners to use the spreadsheet without requiring access to certain types of site-specific data such as traffic volumes, construction history, or other information that may not be readily available.


• The spreadsheet does not directly account for a driver’s destination or origin unless the driver is traveling straight through the interchange on the same route from approach to departure. While each exit and entrance ramp is included in the analysis, the spreadsheet does not directly document the series of decisions an exiting or entering driver would have to make for all of the origin-destination combinations in a given interchange. In other words, it does not estimate the complexity of a path from one route to another; it only describes complexity along the same route. For example, missing movements were not originally included in the spreadsheet, but consideration for the missing movements was added to help describe how some interchanges are more complex because of what is absent rather than what is present.


• The spreadsheet does not account for interactions between factors. There was a great deal of discussion during the early steps in the process to develop the spreadsheet concerning how one factor might affect another so that the combination of the two factors added more complexity than just the sum of the two factors individually. A proper exploration of interaction would be a very time consuming and complicated process and could not be adequately addressed in this study.


• While the spreadsheet does consider C-D roads within the variable for multiple destinations from a single ramp, it is unclear whether the full effect of C-D roads is truly addressed. C-D roads help remove merging, diverging, and weaving maneuvers from the main lanes, thus helping reduce complexity for through drivers. However, C-D roads may actually be more complex than traditional ramps because of the need to exit a substantial distance upstream of where a driver would expect to exit. That effect is not captured in the spreadsheet.


• The spreadsheet does not fully capture the effect of adjacent interchanges. While the nearest upstream and downstream ramp is documented within the spreadsheet, the full effect of that ramp as part of another potentially complex interchange is not included in the analysis. Within the study sites compiled for this spreadsheet, there were three sets of interchanges that are either adjoining or in very close proximity. The two Oregon sites (OR-1 and OR-2) are a short distance apart, and both are constrained by the boundaries of the Willamette River. It is possible that the close proximity of the two interchanges makes traversing them more complex than if they were apart.
  Two Virginia sites (VA-1 and VA-2) are adjacent on I-395, and all three Delaware sites are close enough that a driver could easily drive through all three in one maneuver, changing routes only once. There could be a cumulative effect of these interchanges being so close together, but a thorough exploration of that effect is beyond the ability of this study.


• The spreadsheet is not designed to accommodate more than four approach legs. The spreadsheet was established to account for four corridors – NB, SB, EB, and WB. Those designations could change somewhat if the interchange in question is not particularly oriented to those directions, but the process for using the spreadsheet is the same if the interchange is quadrivial (i.e., having four roads meeting at a point). However, an arguably more complex interchange is one with more than four approaches (i.e., superquadrivial). The majority of those submitted for New York are in this category. It is reasonable that these interchanges are more complex than those evaluated because of the additional legs that must be considered. Unfortunately, expanding the spreadsheet to account for those additional legs would make for an unwieldy spreadsheet, and it is unclear whether a direct comparison between quadrivial and superquadrivial interchanges would be valid.


• As previously mentioned, the spreadsheet does not account for traffic volumes. An implied connection can be made between the number of lanes and traffic volumes, but volumes are not directly requested in the set of input data. Similarly, the volume-to-capacity ratio or the level of service is not requested in the spreadsheet. Those variables could also have an effect on the complexity of an interchange, but they are not design characteristics and were deemphasized for this study.

Additional Considerations

In addition to the features and limitations of the spreadsheet, additional items that may be considered in understanding how the spreadsheet functions are provided in the following list (these items could also be topics for further exploration):

• The topic of missing movements has been mentioned previously in this appendix. The concept is that a missing movement prevents a driver on a given approach from directly accessing a different approach. It may be possible to go from one to the other but only through a series of maneuvers such as U-turns or multiple exits and entrances. Originally, missing movements were not included because the spreadsheet only evaluated existing ramps – the spreadsheet could not consider a ramp that did not exist. An adjustment was made to include missing movements, but it is unclear whether the scoring or weight properly quantifies the relative complexity of this site characteristic.


• The results of the spreadsheet (i.e., the scores for each interchange and each individual approach) are dependent on the high/low threshold values and weights, which were subjectively determined by the research team with input from reviewers. Even the fact that the weights were originally designed to generate a 100-point total for ease of observation may affect the results; allowing for a different point total could provide a different means of establishing the weights. The research team believes that the 100-point total is beneficial and aids the user in understanding the results. Researchers also believe the sets of weights and threshold values presented are reasonable, given the consistency in the relative scores and groupings that resulted from the variety of combinations tested. The team also recognizes that a different set of weights and values that produce somewhat different scores could be developed on a reasonable basis.


• A full sensitivity analysis would help determine whether some weights or threshold values are inappropriately affecting the scores. A partial analysis was conducted on selected variables, but a full analysis was not possible in this study. For example, it is unclear whether the number of general purpose lanes is optimally accounted for in the spreadsheet. It is used as a surrogate for traffic volume and provides an indication of complexity if a driver must make additional lane changes, but it is unknown how sensitive the score is to the presence of two through lanes instead of three or four (if the threshold value was changed) and whether the presence of three general purpose lanes is truly as complex as the presence of a concrete barrier within 4 ft of the left side of the travel way. The research team believes that the sets of weights and threshold values presented are reasonable, but the team also recognizes that a reasonable approach could produce a different set of weights and values with somewhat different scores.


• Another topic of consideration is how study distance is measured. The spreadsheet includes all of the distance a driver must travel to navigate through the interchange, which means that the distance is measured from the point immediately downstream of the nearest ramp in the adjacent upstream interchange to the point of the nearest ramp for the succeeding interchange. This distance may be too large to sufficiently capture the effects of some calculated values, such as ramp density. The added distance may understate ramp density effects, particularly for cloverleaf interchanges that have segments of dense ramp locations (i.e., a cluster of ramps) followed by a long distance between ramps, resulting in a lower ramp density over the entire study distance.


• The use of the average approach score to determine the overall interchange score may deemphasize a particularly complex approach. It is possible that the use of the highest approach score would be beneficial in determining the complexity of an interchange, but that method could also deemphasize a relatively simple approach. As stated previously, practitioners could develop reasonable explanations for using either method.


• Operating speed and posted speed limit are not accounted for in this spreadsheet, and some of the sites had lower posted speed limits than others with similar or lower scores. For example, NY-3 had a posted limit of 45 mi/h on its major route; however, because of its ramp density and presence of left entrances and exits, it had a higher score than other sites with higher speed limits. It is unclear to what extent lower operating speeds would mitigate some of the complexity in an interchange such as NY-3 compared to other sites with fewer complex elements but higher speeds.

SUMMARY

Researchers were tasked with developing a tool that could aid practitioners in assessing the complexity of a freeway interchange and objectively compare it to other interchanges. The focus of such a tool was on geometric design factors and related effects on driver expectancy and driver workload. Researchers considered a variety of factors and formats, ultimately developing a spreadsheet tool in which users could enter site characteristics and receive a numerical complexity score for a given interchange. After several revisions, researchers settled on a spreadsheet tool that considers the effects of 32 weighted factors on as many as 4 approaches within a given interchange. The weights range in value from 1 to 5, and the sum of the 32 weights is 100 (see table 19). The estimated impact of each factor is given points, which, when multiplied by the weight, produces a weighted score on a 1,000-point scale for each approach and for the interchange as a whole.

To determine how well the spreadsheet tool would evaluate interchanges, the research team used the spreadsheet to review 28 existing sites in 11 States. The sites were submitted by State transportation departments on the basis of their perceived complexity. The 28 sites were divided into 4 distinct groups based on the spreadsheet scores ranging from a high of 590 to a low of 180. Sites with similar scores were in the same group and were viewed as having similar levels of complexity. Researchers tested multiple combinations of weights to develop scores for the 28 sites. While individual site scores changed as the weights changed, the final set of weights produced results similar to the rankings and groupings of the study sites determined by the research team. This indicates that for the characteristics included in this spreadsheet, the results produced a general sense of the relative complexity of the interchanges studied.

In summary, the complex interchange spreadsheet tool is a useful tool for objectively comparing the complexity of multiple interchanges and determining what characteristics contribute to that complexity. There may be other variables that could be useful additions to the factors already included, and it is possible that a different distribution of weights and threshold values may produce a reasonable set of scores that varies from those presented in this report; however, these scores allow the user to evaluate one or more interchanges to identify potential problems that drivers may face as they travel through those interchanges. Consideration of these issues can help practitioners identify potential countermeasures either through the use of traffic control devices or, ideally, through the use of revised designs to mitigate the site characteristics that are potentially problematic.