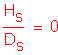LRFD Steel Girder SuperStructure Design Example
Pile Foundation Design Example Design Step P
Table of Contents
Design Step P.1 - Define Subsurface Conditions and Any Geometric Constraints
Design Step P.2 - Determine Applicable Loads and Load Combinations
Design Step P.3 - Factor Loads for Each Combination
Design Step P.4 - Verify Need for a Pile Foundation
Design Step P.5 - Select Suitable Pile Type and Size
Design Step P.6 - Determine Nominal Axial Structural Resistance for Selected Pile Type / Size
Design Step P.7 - Determine Nominal Axial Geotechnical esistance for Selected Pile Type / Size
Design Step P.8 - Determine Factored Axial Structural Resistance for Single Pile
Design Step P.9 - Determine Factored Axial Geotechnical Resistance for Single Pile
Design Step P.10 - Check Drivability of Pile
Design Step P.11 - Do Preliminary Pile Layout Based on Factored Loads and Overturning Moments
Design Step P.12 - Evaluate Pile Head Fixity
Design Step P.13 - Perform Pile Soil Interaction Analysis
Design Step P.14 - Check Geotechnical Axial Capacity
Design Step P.15 - Check Structural Axial Capacity in lower portion of pile)
Design Step P.16 - Check Structural Axial Capacity in Combined Bending and Axial Load (upper portion of pile)
Design Step P.17 - Check Structural Shear Capacity
Design Step P.18 - Check Maximum Horizontal and Vertical Deflection of Pile Group at Beam Seats Using Service Load Case
Design Step P.19 - Additional Miscellaneous Design Issues
References
Design Step P.1 - Define Subsurface Conditions and Any Geometric Constraints
This task involves determining the location and extent of soil and rock materials beneath the proposed abutment and determining engineering design properties for each of those materials. It also includes identification of any specific subsurface conditions that may impact the performance of the structure. The design of the foundation system needs to address any identified issues.
A subsurface investigation was conducted at the site. Two test borings were drilled at each substructure unit. Soils were sampled at 3 foot intervals using a split spoon sampler in accordance with ASTM D-1586. Rock was continuously sampled with an N series core barrel in accordance with ASTM D-2113.
For Abutment 1, one boring was drilled at each side of the abutment. These borings are illustrated graphically in Section A1 below.
Refer to Design Step 1 for introductory information about this design example. Additional information is presented about the design assumptions, methodology, and criteria for the entire bridge, including the Pile Foundation Design.
The following units are defined for use in this design example:
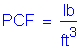
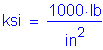
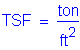
![]()
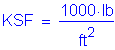
![]()
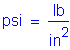
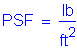
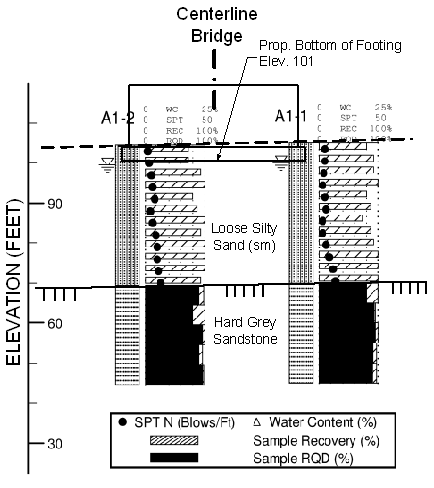
Figure P-1 Section A1 - Subsurface Conditions at Abutment 1
Evaluation of Section A1 indicates that subsurface conditions are relatively uniform beneath the proposed abutment consisting of essentially 2 materials.
Loose silty sand was encountered in the top 35 feet of each boring. This material is non-plastic and contains about 15% fine material. Below a depth of about 5' the soil is saturated.
Rock was encountered at about elevation 70 in both borings. The rock consists of a hard gray sandstone. Fractures are tight with no infilling and occur at a spacing of 1-3'; primarily along bedding planes which are horizontal. Slight weathering was observed in the upper 1' foot of the rock but the remainder of the rock is unweathered.
Special Geotechnical Considerations:
The loose fine sandy soils could be subject to liquefaction under seismic loading. Liquefaction is a function of the anticipated maximum earthquake magnitude and the soil properties. If liquefaction is a problem, the soils can not be relied upon to provide lateral support to deep foundation systems. For this example it is assumed that the potential for liquefaction has been evaluated and has been found to be negligible. (Note: Seed and Idriss (NCEER-97-0022) provides more up to date material for evaluation of liquefaction)
C10.5.4, SAppendix A10
The weight of the approach embankment will cause compression of the loose soil horizon. The granular material should compress essentially elastically with little or no long term consolidation. However, since the full height abutment will likely be placed prior to completion of the approach embankment in the vicinity of the abutment, soil compression beneath the abutment must be accounted for in foundation design. For shallow foundations, this compression will result in settlement and rotation of the footing. For deep foundations this compression could result in negative skin friction (downdrag) loads on the foundation elements; particularly in the back row of piles.
S10.7.1.4, C10.7.1.4
Development of Parameters for Design:
Layer 1 - Soil
Depth:
Assuming a bottom of footing elevation of 101 FT and a top of rock elevation of 70 FT as described above:
![]()
Unit Weight ( Υ ):
Consider relevant published data when selecting design parameters. For unit weights of in-situ soil materials, a good reference is NAVFAC DM7.1-22. Based on this reference, general and local experience, and the above description of the soil horizon as loose silty sand, the unit weights were selected as follows:
C10.4.1
Dry unit weight: ![]()
Wet unit weight: ![]()
Unit weight of water: ![]()
Effective unit weight: ![]()
![]()
Angle of internal friction ( φ ):
The angle of internal friction can be estimated based on correlation to Standard Penetration Test (SPT) N values. The raw SPT N-values determined in the test borings must be corrected for overburden pressure as follows:
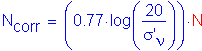
SEquation 10.7.2.3.3-4
where:
Corrected SPT blow count (Blows/FT)
Note: The formula above is generally considered valid for values of σ' > 0.25 TSF (Bowles 1977): ![]()
SPT blow count (Blows/FT): ![]()
Vertical effective stress at bottom of sample (TSF): ![]()
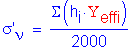
where:
Thickness of soil layer i above point being considered (FT):
Effective unit weight of soil layer i (PCF):
Number of soil layer under consideration:
This formula is implemented for each of the borings below. Wet unit weight is used for the soil above the water table and effective unit weight is used for the soil below the water table.
| Depth to Top of Sample (FT) | Depth to Bottom of Sample (FT) | Ueff i (PCF) | sn' (TSF) | N Blows/Ft (BPF) | Ncorr Blows/Ft (BPF) |
|---|---|---|---|---|---|
| Boring A1-1 | |||||
| 0 | 1.5 | 110 | 0.0825 | 5 | 9 |
| 3 | 4.5 | 110 | 0.2475 | 5 | 7 |
| 6 | 7.5 | 47.6 | 0.3189 | 4 | 6 |
| 9 | 10.5 | 47.6 | 0.3903 | 3 | 4 |
| 12 | 13.5 | 47.6 | 0.4617 | 5 | 6 |
| 15 | 16.5 | 47.6 | 0.5331 | 6 | 7 |
| 18 | 19.5 | 47.6 | 0.6045 | 3 | 4 |
| 21 | 22.5 | 47.6 | 0.6759 | 3 | 3 |
| 24 | 25.5 | 47.6 | 0.7473 | 6 | 7 |
| 27 | 28.5 | 47.6 | 0.8187 | 9 | 10 |
| 30 | 31.5 | 47.6 | 0.8901 | 12 | 12 |
| 33 | 34.5 | 47.6 | 0.9615 | 14 | 14 |
| Boring A1-2 | |||||
| 0 | 1.5 | 110 | 0.0825 | 2 | 4 |
| 3 | 4.5 | 110 | 0.2475 | 3 | 4 |
| 6 | 7.5 | 47.6 | 0.3189 | 5 | 7 |
| 9 | 10.5 | 47.6 | 0.3903 | 6 | 8 |
| 12 | 13.5 | 47.6 | 0.4617 | 8 | 10 |
| 15 | 16.5 | 47.6 | 0.5331 | 4 | 5 |
| 18 | 19.5 | 47.6 | 0.6045 | 6 | 7 |
| 21 | 22.5 | 47.6 | 0.6759 | 9 | 10 |
| 24 | 25.5 | 47.6 | 0.7473 | 10 | 11 |
| 27 | 28.5 | 47.6 | 0.8187 | 10 | 11 |
| 30 | 31.5 | 47.6 | 0.8901 | 11 | 11 |
| 33 | 34.5 | 47.6 | 0.9615 | 13 | 13 |
Table P-1 Calculation of Corrected SPT Blow Count
Find average values for zone between bottom of footing and top of rock. This means ignoring the first two values of each boring.
![]()
![]()
![]()
![]()
The correlation published in FHWA-HI-96-033 Page 4-17 (after Bowles, 1977) is used to determine the angle of internal friction. This correlation is reproduced below.
| Description | Very Loose | Loose | Medium | Dense | Very Dense |
|---|---|---|---|---|---|
| Ncorr = | 0-4 | 4-10 | 10-30 | 30-50 | >50 |
| jf = | 25-30o | 27-32o | 30-35o | 35-40o | 38-43o |
| a = | 0.5 | 0.5 | 0.25 | 0.15 | 0 |
| b = | 27.5 | 27.5 | 30 | 33 | 40.5 |
Table P-2 Correlation
This correlation can be expressed numerically as: ![]()
where:
a and b are as listed in Table P-2.
![]()
![]()
![]()
Thus
![]()
![]() o say
o say
![]() o
o
Modulus of elasticity (E):
Estimating E0 from description
STable 10.6.2.2.3b-1
Loose Fine Sand E0= 80 - 120 TSF
Estimating E0 from Ncorr
Note, in Table 10.6.2.2.3b-1 N1 is equivalent to Ncorr
Clean fine to medium sands and slightly silty sands
![]()
STable 10.6.2.2.3b-1
![]()
![]()
![]()
Based on above, use:
![]()
![]()
Poisons Ratio ( ν ):
Estimating ν from description
STable 10.6.2.2.3b-1
Loose Fine Sand: ![]()
Shear Modulus (G):
From Elastic Theory:
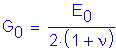
![]()
![]()
Coefficient of variation of subgrade reaction (k):
As per FHWA-HI-96-033, Table 9-13:
This is used for lateral analysis of deep foundation elements
Submerged Loose Sand
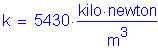
![]()
Layer 2 - Rock:
Depth:
Rock is encountered at elevation 70 and extends a minimum of 25 FT beyond this point.
Unit Weight ( Υ ):
Determined from unconfined compression tests on samples of intact rock core as listed below:
| Boring No. | Depth (FT) | U (PCF) |
|---|---|---|
| A1-1 | 72.5 | 152 |
| A1-1 | 75.1 | 154 |
| A1-2 | 71.9 | 145 |
| A1-2 | 76.3 | 153 |
| P1-1 | 81.2 | 161 |
| P1-2 | 71.8 | 142 |
| A2-1 | 76.3 | 145 |
| A2-2 | 73.7 | 151 |
| Average U | 150.375 | |
Table P-3 Unit Weight
![]()
Unconfined Compressive Strength (q):
Determined from unconfined compression tests on samples of intact rock core as listed below:
| Boring No. | Depth (FT) | qu (PSI) |
|---|---|---|
| A1-1 | 72.5 | 12930 |
| A1-1 | 75.1 | 10450 |
| A1-2 | 71.9 | 6450 |
| A1-2 | 76.3 | 12980 |
| P1-1 | 81.2 | 14060 |
| P1-2 | 71.8 | 6700 |
| A2-1 | 76.3 | 13420 |
| A2-2 | 73.7 | 14890 |
| Average qu | 11485 | |
Table P-4 Unconfined Compressive Strength
![]()
Modulus of elasticity (E):
STable 10.6.2.2.3d-2
This is to be used for prediction of deep foundation response
For sandstone, Average: ![]()
![]()
Poisons Ratio ( ν ):
STable 10.6.2.2.3d-1
This is to be used for prediction of pile tip response
For sandstone, Average: ![]()
Shear Modulus (G):
From elastic theory
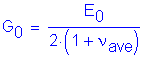
![]()
![]()
Rock Mass Quality:
Rock mass quality is used to correct the intact rock strength and intact modulus values for the effects of existing discontinuities in the rock mass. This is done through empirical correlations using parameters determined during core drilling.
Data from the test borings is summarized below:
| Depth (FT) | Run Length (FT) | Recovery (%) | RQD (%) |
|---|---|---|---|
| Boring A1-1 | |||
| 35 | 5 | 100 | 80 |
| 40 | 5 | 96 | 94 |
| 45 | 5 | 100 | 96 |
| 50 | 5 | 98 | 92 |
| 55 | 5 | 98 | 90 |
| Boring A1-2 | |||
| 35 | 5 | 98 | 90 |
| 40 | 5 | 100 | 80 |
| 45 | 5 | 100 | 96 |
| 50 | 5 | 96 | 90 |
| 55 | 5 | 98 | 96 |
| Averages | 98.4 | 90.4 | |
Table P-5 Rock Mass Quality
Design Step P.2 - Determine Applicable Loads and Load Combinations
Loads and load combinations are determined elsewhere in the design process. The critical load cases for evaluation of foundation design are summarized below:
The load combination that produces the maximum vertical load on the foundation system. This will typically be a Strength I and a Service I load case with the maximum load factors applied.
The load combination that produces the maximum overturning on the foundation which will tend to lift a spread footing off the bearing stratum or place deep foundation elements in tension.
The load combination that produces the maximum lateral load. If several combinations produce the same horizontal load, select the one with the minimum vertical load as this will be critical for evaluation of spread footing sliding or response of battered deep foundations. In some cases, particularly deep foundations employing all vertical elements, the highest lateral load and associated highest vertical load should also be evaluated as this case may produce higher foundation element stress and deflections due to combined axial load and bending in the foundation elements.
Design Step P.3 - Factor Loads for Each Combination
It is extremely important to understand where the loads are being applied with respect to foundation design. In this case the loads were developed based on an assumed 10' 3" wide by 46' 10 1/2" long footing that is offset behind the bearings a distance of 1' 9". The loads are provided at the horizontal centroid of the assumed footing and at the bottom of that footing. A diagram showing the location and direction of the applied loads is provided below.
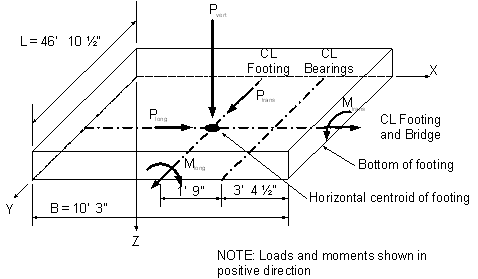
Figure P-2 Application of Loads
| LIMIT STATE | AXIAL FORCE Pvert (K) | LONG MOMENT Mlong (K-FT) | TRANS MOMENT Mtrans (K-FT) | LATERAL LOAD (IN LONG. DIR.) Plong (K) | LATERAL LOAD (IN TRANS. DIR.) Ptrans (K) | |
|---|---|---|---|---|---|---|
| Maximum Vertical Load | STR-I MAX/FIN | 2253 | 7693 | 0 | 855 | 0 |
| SER-I MAX/FIN | 1791 | 4774 | 162 | 571 | 10 | |
| Maximum Overturning | STR-I MIN/FIN | 1860 | 7291 | 0 | 855 | 0 |
| SER-I MIN/FIN | 1791 | 4709 | 162 | 568 | 10 | |
| Maximum Lateral Load | STR-III MAX/FIN | 1815 | 6374 | 508 | 787 | 37 |
| SER-I MAX/FIN | 1791 | 4774 | 162 | 571 | 10 |
Table P-6 Summary of Factored Loads
It should be noted that the calculations performed in Design Step P are based on preliminary pile foundation design forces. In an actual design, the geotechnical engineer would need to revisit the pile foundation design calculations and update the results based on the final design bottom of booting forces given at the end of Design Step 7.7.
Design Step P.4 - Verify Need for a Pile Foundation
Evaluate a spread footing design:
Check vertical capacity:
Presumptive Bearing Capacity for loose sand with silt (SM)
Presumptive bearing capacity ![]()
STable 10.6.2.3.1-1
![]()
Presumptive bearing capacity is a service limit state, thus compare against maximum service load.
S10.5.2
From Design Step P.3, the Maximum service load is ![]()
The Required area: ![]()
The length of the footing is controlled by the length of the abutment step required to support the steel beams and the approach roadway. This is determined from previous geometry calculations.
Maximum possible length of footing ![]()
Preliminary minimum required width ![]()
Excessive loss of contact:
This is a strength limit state thus use strength loads for the case of maximum overturning which is STR I Min.
S10.5.3
Determine the maximum eccentricity eB in the direction parallel to the width of the footing (B)
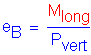
From the loads obtained in Design Step P.3, ![]()
![]()
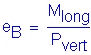
![]()
To prevent excessive loss of contact eB must be less than B/4.
S10.6.3.1.5
Width of the footing: ![]()
![]()
In order to resolve the bearing pressure and eccentricity issue, the footing will have to be widened and the centroid shifted toward the toe. This can be accomplished by adding width to the toe of the footing. Note that the issue could also be resolved by adding width to the heel of the footing, which would increase the weight of soil that resists overturning. This would require recalculation of the loads and was not pursued here.
In order to satisfy bearing pressure and eccentricity concerns, the footing width is increased incrementally until the following two criteria are met:
![]() Based on Strength Loads
Based on Strength Loads
![]() >
> ![]() Based on Service Loads
Based on Service Loads
Where B' is the effective footing width under eccentric load
![]()
SEquation 10.6.3.1.5-1
For the Strength Load case:
| Footing width B (FT) | Distance from heel to Centroid of footing (FT) | Distance from heel to centroid of load (FT) | eB (FT) | B/4 (FT) |
|---|---|---|---|---|
| 10.25 | 5.13 | 9.05 | 3.92 | 2.56 |
| 11.00 | 5.50 | 9.05 | 3.55 | 2.75 |
| 12.00 | 6.00 | 9.05 | 3.05 | 3.00 |
| 13.00 | 6.50 | 9.05 | 2.55 | 3.25 |
| 14.00 | 7.00 | 9.05 | 2.05 | 3.50 |
| 15.00 | 7.50 | 9.05 | 1.55 | 3.75 |
| 16.00 | 8.00 | 9.05 | 1.05 | 4.00 |
| 17.00 | 8.50 | 9.05 | 0.55 | 4.25 |
Table P-7 Excessive Loss of Contact - Strength
For the Strength Load Case, the condition was satisfed first when the width of the footing B = 13.00 FT
For the Service Load Case
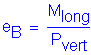
From the loads obtained from Design Step P.3, ![]()
![]()
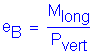
![]()
| Footing width B (FT) | Distance from heel to Centroid of footing (FT) | Distance from heel to centroid of load (FT) | eB (FT) | B' (FT) |
|---|---|---|---|---|
| 10.25 | 5.13 | 7.80 | 2.67 | 4.91 |
| 11.00 | 5.50 | 7.80 | 2.30 | 6.41 |
| 12.00 | 6.00 | 7.80 | 1.80 | 8.41 |
| 13.00 | 6.50 | 7.80 | 1.30 | 10.41 |
| 14.00 | 7.00 | 7.80 | 0.80 | 12.41 |
| 15.00 | 7.50 | 7.80 | 0.30 | 14.41 |
| 16.00 | 8.00 | 7.80 | -0.21 | 16.41 |
Table P-8 Presumptive Bearing Pressure - Service
For the Service Load Case, the condition was satisfed first when the width of the footing B = 15.00 FT
The first width to satisfy both conditions is 15.00 FT. Which would require the toe of the footing to be extended:
![]()
![]()
This increase may not be possible because it may interfere with roadway drainage, roadside utilities, or the shoulder pavement structure. However, assume this is not the case and investigate potential settlement of such a footing.
Settlement is a service limit state check.
For the granular subsoils, settlement should be esentially elastic thus Settlement (S0) is computed from:
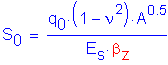
SEquation 10.6.2.2.3b-1
Assume the footing is fully loaded, thus q0 is the presumptive bearing capacity and effective loaded area is as calculated above
Average bearing pressure on loaded area: ![]()
![]()
Effective are of footing: ![]()
Length of footing
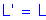
Width of the footing
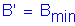
Therfore, the Effective Area is
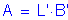
Modulus of elasticity of soil, from Design Step P.1: ![]()
Poisson's ratio of soil, from Design Step P.1: ![]()
Shape factor for rigid footing: ![]()
![]()
![]()
From Table 10.6.2.2.3b-2 for rigid footing:
| L'/B' | bz |
|---|---|
| 3 | 1.15 |
| 5 | 1.24 |
STable 10.6.2.2.3b-2
Table P-9 Rigid Footing
By interpolation, at ![]()
![]()
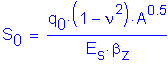
![]()
![]()
Note: This computation assumes an infinite depth of the compressible layer. Other computation methods that allow for the rigid base (NAVFAC DM-7.1-211) indicate the difference between assuming an infinite compressible layer and a rigid base at a depth equal to 3 times the footing width (H/B = 3) below the footing can be estimated by computing the ratio between appropriate influence factors (I) as follows:
As per NAVFAC DM7.1-212, and DM7.1-213:
I for rigid circular area over infinite halfspace: ![]()
I for rigid circular area over stiff base at H/B of 3:
![]()
The influence value determined above is for a Poisson's ratio of 0.33. A Poisson's ration of 0.25 is used for the soil. This difference is small for the purposes of estimating elastic settlement.
Ratio of I values:
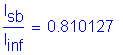
Since I is directly proportional to settlement, this ratio can be multiplied by S0 to arrive at a more realistic prediction of settlement of this footing.
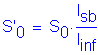
![]()
This settlement will occur as load is applied to the footing and may involve some rotation of the footing due to eccentricities of the applied load. Since most of the loads will be applied after construction of the abutment (backfill, superstructure, deck) this will result in unacceptable displacement.
The structural engineer has determined that the structure can accommodate up to 1.5" of horizontal displacement and up to 0.5" vertical displacement. Given the magnitude of the predicted displacements, it is unlikely this requirement can be met. Thus, a deep foundation system or some form of ground improvement is required.
Note that the above calculation did not account for the weight of the approach embankment fill and the effect that this will have on the elastic settlement. Consideration of this would increase the settlement making the decision to abandon a spread footing foundation even more decisive.
Design Step P.5 - Select Suitable Pile Type and Size
It will be assumed that for the purposes of this example, ground improvement methods such as vibro-flotation, vibro replacement, dynamic deep compaction, and others have been ruled out as impractical or too costly. It is further assumed that drilled shaft foundations have been shown to be more costly than driven pile foundations under the existing subsurface conditions (granular, water bearing strata). Thus a driven pile foundation will be designed.
Of the available driven pile types, a steel H-pile end bearing on rock is selected for this application for the following reasons.
It is a low displacement pile which will minimize friction in the overlying soils.
It can be driven to high capacities on and into the top weathered portion of the rock.
It is relatively stiff in bending thus lateral deflections will be less than for comparably sized concrete or timber piles.
Soils have not been shown to be corrosive thus steel loss is not an issue.
To determine the optimum pile size for this application, consideration is given to the following:
1) Pile diameter:
H-Piles range in size from 8 to 14 inch width. Since pile spacing is controlled by the greater of 30 inches or 2.5 times the pile diameter (D); pile sizes 12 inches and under will result in the same minimum spacing of 30 inches. Thus for preliminary analysis assume a 12 inch H-Pile.
2) Absolute Minimum Spacing:
Per referenced article, spacing is to be no less than:
![]()
S10.7.1.5
Where the pile diameter: ![]()
![]()
3) Minimum pile spacing to reduce group effects:
As per FHWA-HI-96-033, Section 9.8.1.1:
Axial group effects for end bearing piles on hard rock are likely to be negligible thus axial group capacity is not a consideration. However, note that the FHWA driven pile manual recommends a minimum c-c spacing of 3D or 1 meter in granular soils to optimize group capacity and minimize installation problems. The designer's experience has shown 3D to be a more practical limit that will help avoid problems during construction.
Lateral group effects are controlled by pile spacing in the direction of loading and perpendicular to the direction of loading.
From Reese and Wang, 1991, Figure 5.3 (personal communication):
For spacing perpendicular to the direction of loading 3D results in no significant group impacts.
As per FHWA-HI-96-033, Section 9.8.4 & NACVFAC DM7.2-241:
For spacing in the direction of loading, various model studies indicate that group efficiency is very low at 3D spacing, moderate at about 5D spacing and near 100% for spacings over about 8D. Thus it is desirable to maintain at least 5D spacing in the direction of the load and preferable to maintain 8D spacing.
Maximum pile spacing
Spacing the piles more than 10 feet c-c results in higher bending moments in the pile cap between each pile and negative bending moments over the top of each pile that may result in additional steel reinforcing or thicker pile caps. Thus it is desirable to keep the pile spacing less than 10 feet c-c.
4) Edge clearance
Referenced section indicates minimum cover: ![]()
S10.7.1.5
Thus for a 12 inch pile, minimum distance from edge of footing to center of pile:
![]()
![]()
5) Maximum pile cap dimensions
The length of the pile cap in the direction perpendicular to the centerline (L) is limited to the width of the abutment. Thus:
From Design Step P.4:
![]()
![]()
The width of the pile cap in the direction parallel to the centerline of the bridge (B) can generally be made wider as required. Initial loadings were developed assuming a width of 10.25 FT thus use this dimension as a starting point.
![]()
Determine the maximum and minimum number of piles that can be placed beneath the cap (See sketch below for definition of variables)
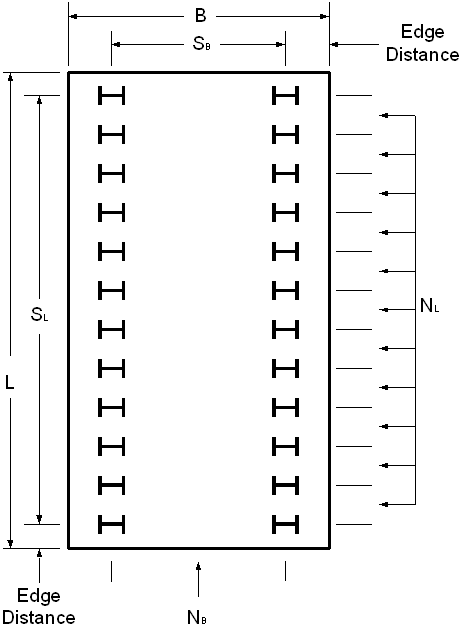
Figure P-3 Plan View of Pile Cap
In B direction:
![]() is defined as: Width of the pile cap - 2 times the edge distance
is defined as: Width of the pile cap - 2 times the edge distance
![]()
![]()
Max number of spaces at 5D spacing (NB)
![]()
![]()
![]()
Minimum number of spaces at 10' each (NB)
![]()
![]()
![]()
Since the number of spaces has to be an integer
![]()
Which results in two rows of piles in the B direction.
In L direction:
![]() is defined as: Width of the pile cap - 2 times the edge distance
is defined as: Width of the pile cap - 2 times the edge distance
![]()
![]()
Max number of spaces at 3D spacing (NL)
![]()
![]()
![]()
Minimum number of spaces at 10' each (NL)
![]()
![]()
![]()
Since the number of spaces has to be an integer
![]() to 14
to 14
Which results in 6 to 15 rows of piles in the L direction.
Determine maximum axial load acting on piles
Using factored loads and diagram below, determine reactions on the front and back pile rows:
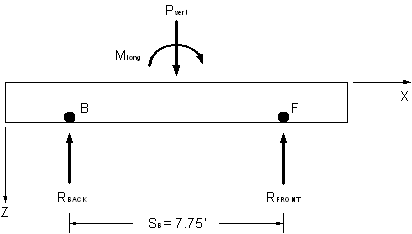
Figure P-4 Section View of Pile Cap
Summing the forces in the z-direction and the moments about point B:
![]()
![]()
![]()
![]()
For STR I max, from Table P.6:
![]()
![]()
![]()
![]()
For STR I min, from Table P.6:
![]()
![]()
![]()
![]()
Max axial load on front row of piles:
![]()
![]()
Since the front row can have 6 - 15 piles,
Max anticipated factored pile load can range between:
![]()
![]()
and
![]()
![]()
Assuming the following:
Axial pile resistance is controlled by structural resistance
SEquation 6.9.2.1-1 and SEquation 6.9.4.1-1
Structural resistance ![]()
NOTE: λ in equation 6.9.4.1-1 is assumed to be zero (because unbraced length is zero) resulting in the simplified equation shown above.
![]()
S6.5.4.2
![]()
NOTE: Grade 36 steel is assumed at this stage even though most H-pile sections are available in higher grades at little or no cost differential. The need for using a higher strength steel will be investigated in future design steps
Compute required pile area to resist the anticipated maximum factored pile load. The required steel area can range between:
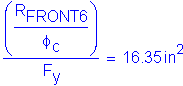 and
and 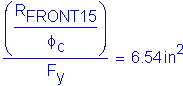
For preliminary layout and design, select: HP 12x53
Properties of HP 12x53:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Note: Plastic section modulus is used to evaluate nominal moment capacity
![]()
![]()
Design Step P.6 - Determine Nominal Axial Structural Resistance for Selected Pile Type / Size
Ultimate axial compressive resistance is determined in accordance with either equation 6.9.4.1-1 or 6.9.4.1-2. The selection of equation is based on the computation of l in equation 6.9.4.1-3 which accounts for buckling of unbraced sections. Since the pile will be fully embedded in soil, the unbraced length is zero and therefore l is zero. Based on this this, use equation 6.9.4.1-1 to calculate the nominal compressive resistance.
S6.9.4.1
![]()
SEquation
6.9.4.1-1
where:
![]()
![]()
![]()
Therefore:
![]()
![]()
Design Step P.7 - Determine Nominal Axial Geotechnical Resistance for Selected Pile Type / Size
Geotechnical axial resistance for a pile end bearing on rock is determined by the CGS method outlined in 10.7.3.5
Nominal unit bearing resistance of pile point, qp
![]()
SEquation 10.7.3.5-1
for which: 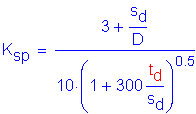
SEquation 10.7.3.5-2
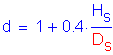
![]()
where:
Average compressive strength of rock core:
From Design Step P.1:
Spacing of discontinuities:
Based on high observed RQD in Design Step P.1 and description of rock:
Width of discontinuities:
Joints are tight as per discussion in Design Step P.1:
Pile width:
HP 12x53 used:
Depth of embedment of pile socketed into rock:
Pile is end bearing on rock:
Diameter of socket:
Assumed but does not matter since Hs = 0:
so:
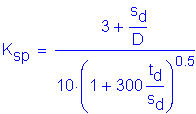
![]()
and:
![]()
Thus:
![]()
![]()
Nominal geotechnical resistance (Qp): ![]()
SEquation 10.7.3.2-3
where:
Nominal unit bearing resistance as defined above:
Area of the pile tip:
Area determined assuming a plug develops between flanges of the H-Pile. This will be the case if the pile is driven into the upper weathered portion of the rock.
Therefore:
![]()
![]()
Design Step P.8 - Determine Factored Axial Structural Resistance for Single Pile
Factored Structural Resistance (Pr):
![]()
SEquation 6.9.2.1
where:
Resistance factor for H-pile in compression, no damage anticipated:
![]()
S6.5.4.2
Nominal resistance as computed in Design Step P.6: ![]()
Therefore:
![]()
Design Step P.9 - Determine Factored Axial Geotechnical Resistance for Single Pile
Factored Geotechnical Resistance (QR): ![]()
SEquation 10.7.3.2-2
Note: remainder of equation not included since piles are point bearing and skin friction is zero.
where:
Resistance factor, end bearing on rock (CGS method):
STable 10.5.5-2
Factor to account for method controlling pile installation:
For this porject, stress wave measurements will be specified on 2% of the piles (a minimum of one per substructure unit) and the capacity will be verified by CAPWAP analysis. Thus:
STable 10.5.5-2
and therefore:
![]()
![]()
Nominal resistance as computed in Design Step P.7: ![]()
Therefore:
![]()
![]()
Note: This is greater than the structural capacity, thus structural capacity controls.
Design Step P.10 - Check Drivability of Pile
Pile drivability is checked using the computer program WEAP. The analysis proceeds by selecting a suitable sized hammer. Determining the maximum pile stress and driving resistance (BPF) at several levels of ultimate capacity and plotting a bearing graph relating these variables. The bearing graph is then entered at the driving resistance to be specified for the job (in this case absolute refusal of 20 BPI or 240 BPF will be used) and the ultimate capacity and driving stress correlating to that driving resistance is read.
If the ultimate capacity is not sufficient, a bigger hammer is specified and the analysis is repeated.
If the driving stress exceeds the permitted driving stress for the pile, a smaller hammer is specified and the analysis is repeated.
 |
Drivability of Piles If a suitable hammer can not be found that allows driving the piile to the required ultimate capacity without exceeding the permissible driving stress, modification to the recommended pile type are necessary. These may include:
|
Develop input parameters for WEAP
Driving lengths of piles
The finished pile will likely be 32-33 feet long which includes a 1 foot projection into the pile cap and up to 1' of penetration of the pile tip into the weathered rock. Therefore assume that 35' long piles will be ordered to allow for some variation in subsurface conditions and minimize pile wasted during cut off.
Distribution and magnitude of side friction
This pile will be primarily end bearing but some skin friction in the overlying sand will develop during driving. This skin friction can be quickly computed using the FHWA computer program DRIVEN 1.0. The soil profile determined in Step P.1 is input and an HP12x53 pile selected. The pile top is set at 4 foot depth to account for that portion of soil that will be excavated for pile cap construction. No driving strength loss is assumed since the H-Pile is a low displacement pile and excess pore pressure should dissipate rapidly in the loose sand. Summary output from the program is provided below.
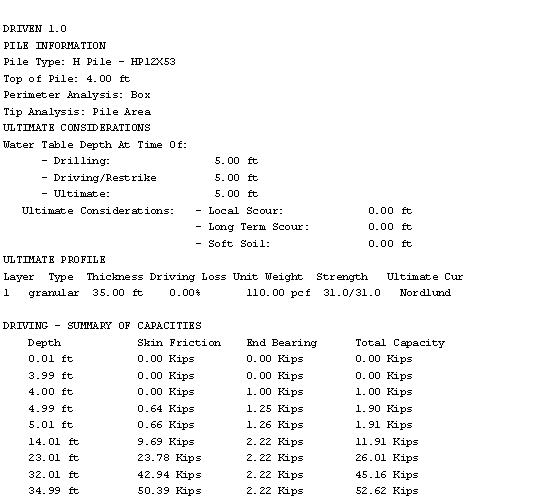
Figure P-5 DRIVEN 1.0 Output
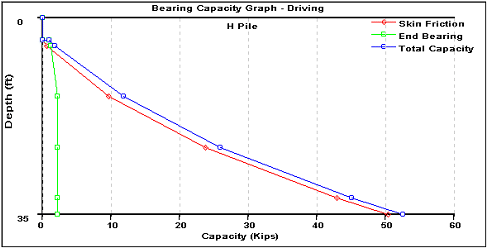
Figure P-6 Bearing Capacity
From this analysis, the side friction during driving will vary in a triangular distribution, and will be about:
![]()
The distribution will start 4 feet below the top of the pile which is:
![]() below the top of the pile.
below the top of the pile.
The desired factored resistance was determined in Design Step P.8 and is controlled by structural resistance of the pile. This value is:
![]()
The ultimate resistance that must be achieved during wave equation analysis will be this value divided by the appropriate resistance factor for wave equation analysis + the estimated side friction.
NOTE: Side friction is added here because downdrag is expected to reduce or reverse the skin friction in the final condition. Therefore, sufficient point capacity must be developed during driving to adequately resist all applied loads plus the downdrag.
![]()
STable 10.5.5-2
From Design Step P.9:
![]()
Thus:
![]()
and
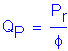
![]()
At this Ultimate point resistance the percent side friction is:
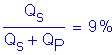
and the resistance required by wave equation analysis is:
![]()
![]()
Soil parameters (use Case damping factors):
 |
Damping Factors Case damping factors are used here because of experience with similar jobs. In general, Smith damping factors are preferred. In this case, the Smith damping factors would likely give very similar results to what is computed using the selected Case damping factors. |
The parameters for loose sand and hard sandstone were estimated based on local experience with similar soils.
Loose Sand
Skin Damping:
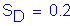
Skin Quake:
Toe Damping:
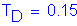
Toe Quake:
Use skin damping and skin quake for pile shaft.
Hard Sandstone
Skin Damping:
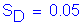
Skin Quake:
Toe Damping:
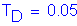
Toe Quake:
Use toe damping and toe quake for pile toe.
Hammer Selection:
As a rule of thumb, start out with a rated energy of 2000 ft-lbs times the steel area of the pile.
Area: ![]()
![]() from Design Step P.5
from Design Step P.5
Rated Energy: ![]()
![]()
Select open ended diesel common to area
DELMAG 12-32 (ID=37) rated at: ![]()
Helmet weight: ![]()
Hammer Cushion Properties:
Area:
Elastic Modulus:
Thickness:
COR:
Hammer Efficiency: ![]()
Permissible Driving Stress:
Driving Stress, ![]()
S10.7.1.16
Note that the equation above was modified to yield stress rather than load.
where:
Resistance factor for driving: ![]()
S6.5.4
Steel yield stress, from Design Step P.5: ![]()
![]()
![]()
Summary of Wave Equations Analysis:
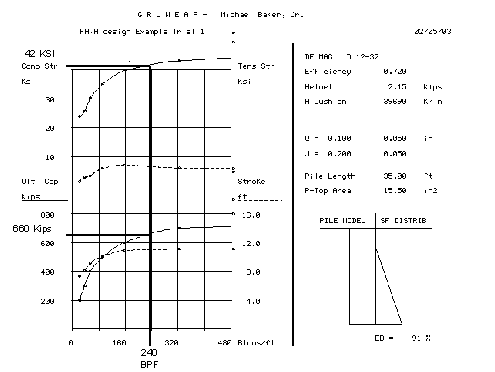
Figure P-7 Wave Equation Analysis
at refusal the pile has an ultimate capacity of ![]()
at refusal the driving stress in the pile is ![]()
Check:
The ultimate capacity exceeds that required
![]()
![]() >
> ![]() OK
OK
The permissible driving stress exceeds the actual value
![]()
![]() >
> ![]()
This condition is not satisfied - no good.
Try reducing hammer energy
DELMAG D 12 (ID=3) rated at
Hammer Cushion Properties same as before
Summary of Wave Equations Analysis:
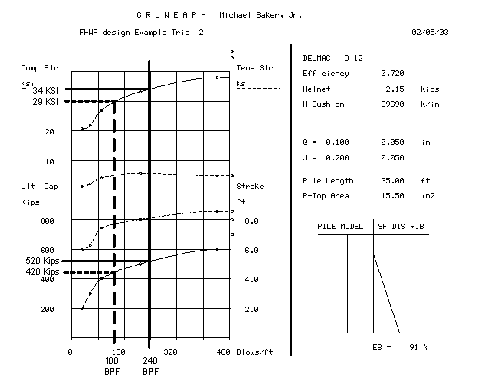
Figure P-8 Wave Equation Analysis
at refusal the pile has an ultimate capacity of ![]()
at refusal the driving stress in the pile is ![]()
Check:
The ultimate capacity exceeds that required
![]()
![]() >
> ![]()
This condition is not satisfied - no good
The permissible driving stress exceeds the actual value
![]()
![]() >
> ![]()
This condition is not satisfied - no good.
A decision must be made at this point:
Is pile drivable to minimum of Ultimate Geotechnical Axial Resistance or Ultimate Structural Resistance without pile damage?
Based on above analysis, no hammer can possibly drive this pile to the required capacity without exceeding the permissible driving stress.
There are 2 approaches to resolving this problem
1) Reduce the factored resistance of the pile to a value that can be achieved without over stressing the pile.
Based on the above bearing graph and allowing for some tolerance in the driving stress (requiring the contractor to select a driving system that produces exactly 32.4 KSI in the pile is unreasonable) a reasonable driven capacity is estimated. Using a minimum driving stress of 29 KSI (0.8 Fy) the penetration resistance is about 100 BPF and the ultimate capacity would be:
![]()
This value includes skin friction during driving which was set in the program to be 9% of the ultimate resistance. Therefore, point resistance at this driving stress would be:
![]()
![]()
and:
![]()
![]()
![]()
2) Increase the yield strength of the pile without increasing the previously computed factored resistance
Using grade 50 steel
Driving Stress: ![]()
S10.7.1.16
(Equation modified to yield stress instead of load)
where:
Resistance factor for driving: ![]()
S6.5.4
Steel yield stress: ![]()
![]()
![]() <
< ![]()
Since option 2 involves little or no additional cost and option 1 will result in significant increase in cost due to required additional piles, select option 2
In this case The Delmag 12-32 produced acceptable driving results.
It can be seen from the results of the wave equation analysis that the driving stress times the pile area is about equal to the mobilized pile capacity. Thus, if the factored structural resistance determined in step P.8 is used as the final design pile resistance, then the ultimate required dynamic capacity determined above is valid and the driving stress associated with this capacity can be estimated by:
Driving Stress 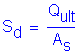
where:
Ultimate required capacity as previously determined by wave equation analysis:
![]()
Pile area, from Design Step 9.5: ![]()
Driving Stress 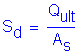
![]()
Thus, so long as the contractor selects a hammer that will produce a driving stress between about 37 and 45 KSI at refusal, an acceptable driven capacity should be achieved during construction.
Using a minimum driving stress of ![]()
![]()
![]()
![]()
![]() As defined previously
As defined previously
![]()
Again, side friction is subtracted from the ultimate capacity since it will be present during driving but will not be present in the final condition. Resistance is based on the point resistance achieved during driving the pile to refusal.
and the minimum driven resistance is
![]()
![]()
![]()
![]()
![]()
Recompute structural resistance based on higher yield steel, as in Design Step P.6
![]()
SEquation 6.9.4.1-1
where
Nominal compressive resistance: ![]()
![]()
![]()
![]()
![]()
The factored axial structural resistance, as in Design Step P.8 is:
![]()
SEquation 6.9.2.1-1
![]()
![]()
Driven capacity controls
Thus final axial resistance of driven pile:
![]()
![]()
Design Step P.11 - Do Preliminary Pile Layout Based on Factored Loads and Overturning Moments
The purpose of this step is to produce a suitable pile layout beneath the pile cap that results in predicted factored axial loads in any of the piles that are less than the final factored resistance for the selected piles. A brief evaluation of lateral resistance is also included but lateral resistance is more fully investigated in step P.13
The minimum number of piles to support the maximum factored vertical load is:
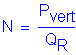
where:
The maximum factored vertical load on the abutment, from Design Step P.3, Load
Case STR I max: ![]()
The final controlling factored resistance for the selected pile type, from
Design Step P.10: ![]()
![]()
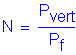
![]() Piles
Piles
Additional piles will be required to resist the over turning moment.
From Design Step P.5, the maximum load that needed to be supported by each row of piles was calculated.
![]()
![]()
The required number of piles in the front row is determined as above.
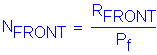
![]() Piles
Piles
Additional load in the corner pile will come from the lateral moment but this is small, so start with 7 piles in the front row.
![]() Piles
Piles
This results in a pile spacing of:
c-c spacing of piles: 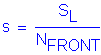
where:
The length of footing available for piles, from Design Step P.5:
![]()
c-c spacing of piles: 
![]()
Set c-c spacing of piles = 7' 4"
This is approaching the maximum pile spacing identified in Step 5 thus set the back row of piles to the same spacing. This will result in the back row of piles being under utilized for axial loads. However, the additional piles are expected to be necessary to help handle lateral loads and to resist downdrag loads that will be applied to the back row only. Further, a load case in which the longitudinal loads such as temperature and braking loads are reversed will increase the loads on the back row.
Thus, the final preliminary layout is diagramed below
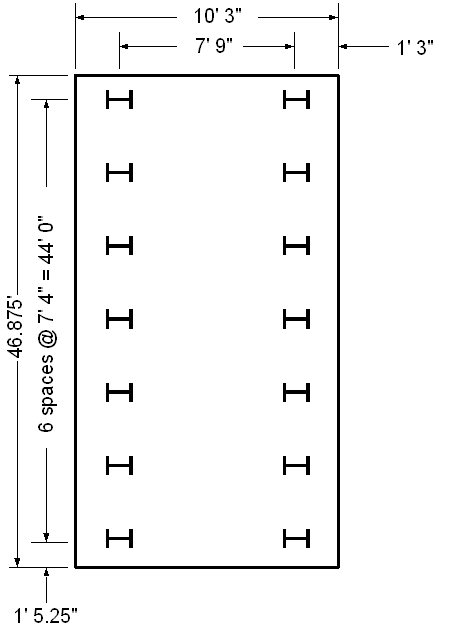
Figure P-9 Plan View of Pile Cap
The spreadsheet below is used to calculate individual pile loads using the
following formula: 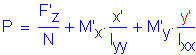
where:
Vertical load and moments applied at the centroid of the pile group:
Distance from centroid of pile group to pile in the x and y directions:
Moment of inertia of the pile group about the y and x axis respectively:
Calculation of Individual Pile Loads on an Eccentrically Loaded Footing:
Input Applied Loads:
At x = 0, y = 0
![]()
![]()
![]()
The coordinate system for the following calculations is provided in Figure
P.10: 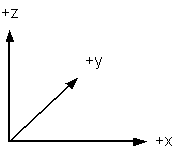
Figure P-10 Coordinate System
Table P-10 is used to calculate the vertical load and moments, and the moment of inertia of the pile group.
| Input Pile Location | Calculated Values | ||||||
|---|---|---|---|---|---|---|---|
| Pile Number | x | y | x' | y' | x' 2 | y' 2 | Pile load |
| 1 | -3.875 | -22 | -3.875 | -22 | 15.01563 | 484 | -19.1221 |
| 2 | 3.875 | -22 | 3.875 | -22 | 15.01563 | 484 | -302.735 |
| 3 | -3.875 | -14.6667 | -3.875 | -14.6667 | 15.01563 | 215.111 | -19.1221 |
| 4 | 3.875 | -14.6667 | 3.875 | -14.6667 | 15.01563 | 215.111 | -302.735 |
| 5 | -3.875 | -7.33333 | -3.875 | -7.33333 | 15.01563 | 53.7778 | -19.1221 |
| 6 | 3.875 | -7.33333 | 3.875 | -7.33333 | 15.01563 | 53.7778 | -302.735 |
| 7 | -3.875 | 0 | -3.875 | 0 | 15.01563 | 0 | -19.1221 |
| 8 | 3.875 | 0 | 3.875 | 0 | 15.01563 | 0 | -302.735 |
| 9 | -3.875 | 7.33333 | -3.875 | 7.333333 | 15.01563 | 53.7778 | -19.1221 |
| 10 | 3.875 | 7.33333 | 3.875 | 7.333333 | 15.01563 | 53.7778 | -302.735 |
| 11 | -3.875 | 14.6667 | -3.875 | 14.66667 | 15.01563 | 215.111 | -19.1221 |
| 12 | 3.875 | 14.6667 | 3.875 | 14.66667 | 15.01563 | 215.111 | -302.735 |
| 13 | -3.875 | 22 | -3.875 | 22 | 15.01563 | 484 | -19.1221 |
| 14 | 3.875 | 22 | 3.875 | 22 | 15.01563 | 484 | -302.735 |
Table P-10 Pile Calculations
Sum of the distances in the x direction is zero.
Sum of the distances in the y direction is zero.
Centroids:
![]()
![]()
Moment of Inertia about the y axis: ![]()
Moment of Inertia about the x axis: ![]()
Resolved loads at Centroid:
![]()
![]()
![]()
![]()
![]()
![]()
Summary of individual pile loads for all load cases:
This table was generated by inserting each load case in the spreadsheet above and recording the resulting pile loads for that load combination.
| Load Case | STR-I MAX/FIN | SER-I MAX/FIN | STR-I MIN/FIN | SER-I MIN/FIN | STR-III MAX/FIN | SER-I MAX/FIN |
|---|---|---|---|---|---|---|
| Fz = | -2253 | -1791 | -1860 | -1791 | -1815 | -1791 |
| Mx = | 0 | 162 | 0 | 162 | 508 | 162 |
| My = | 7693 | 4774 | 7291 | 4709 | 6374 | 4774 |
| Pile No. | ||||||
| 1 | -19.1 | -41.1 | 1.5 | -42.3 | -15.9 | -41.1 |
| 2 | -302.7 | -217.1 | -267.3 | -215.9 | -250.8 | -217.1 |
| 3 | -19.1 | -40.7 | 1.5 | -41.9 | -14.6 | -40.7 |
| 4 | -302.7 | -216.7 | -267.3 | -215.5 | -249.6 | -216.7 |
| 5 | -19.1 | -40.3 | 1.5 | -41.5 | -13.4 | -40.3 |
| 6 | -302.7 | -216.3 | -267.3 | -215.1 | -248.4 | -216.3 |
| 7 | -19.1 | -39.9 | 1.5 | -41.1 | -12.1 | -39.9 |
| 8 | -302.7 | -215.9 | -267.3 | -214.7 | -247.1 | -215.9 |
| 9 | -19.1 | -39.5 | 1.5 | -40.7 | -10.9 | -39.5 |
| 10 | -302.7 | -215.5 | -267.3 | -214.3 | -245.9 | -215.5 |
| 11 | -19.1 | -39.1 | 1.5 | -40.3 | -9.7 | -39.1 |
| 12 | -302.7 | -215.1 | -267.3 | -213.9 | -244.7 | -215.1 |
| 13 | -19.1 | -38.7 | 1.5 | -39.9 | -8.4 | -38.7 |
| 14 | -302.7 | -214.7 | -267.3 | -213.5 | -243.4 | -214.7 |
| Maximum | -302.7 | -217.1 | -267.3 | -215.9 | -250.8 | -217.1 |
| Minimum | -19.1 | -38.7 | 1.5 | -39.9 | -8.4 | -38.7 |
Table P-11 Individual Loads for All Load Cases
Pile loads range between -302.7 K in compression and 1.5 K in tension for all load cases.
The maximum compressive load is reasonably close to the factored resistance for the selected pile and the tension load is minimized thus this is a reasonable layout with respect to axial load.
Evaluate lateral loads:
If all piles are vertical they can all be assumed to take an equal portion of the applied horizontal load since group effects have been minimized by keeping the pile spacing large enough.
The controlling criterion with respect to horizontal loads on vertical piles is usually deflection which is a service load case. Looking at the maximum horizontal loads in section P.3, it can be seen that the transverse loads are relatively small and can be ignored for the purposes of this step. The maximum longitudinal service load is:
![]()
Number of piles: ![]()
Thus, load per pile: 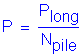
![]()
 |
Lateral Capacity The design chart used below to estimate the lateral capacity of steel H-Piles is one of many methods available to the designer. Brohms method can be used to estimate ultimate capacity (strength limit state) and various published elastic solutions may be used to estimate deflection (service limit state). Pressumptive allowable lateral capacities based on the designer's experience (service limit state) may be used or a preliminary P-y analysis using COM624 may be performed at this point to assist in initial pile group layout |
Based on the design chart below, the maximum service load per pile for an assumed
1.5" deflection (38mm) is: ![]()
From PennDOT DM4 Appendix F-20:
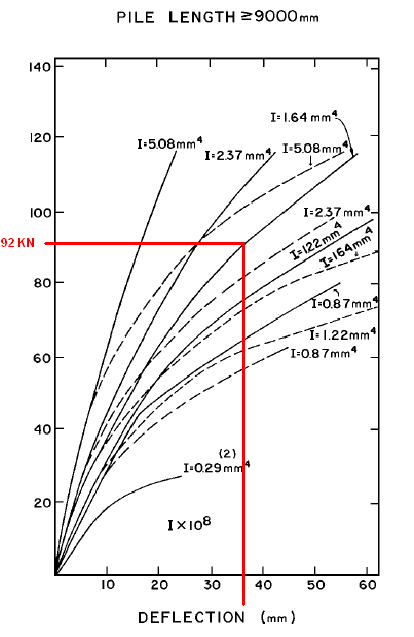
Figure P-11 Maximum Service Load Per Pile
Notes on chart:
Solid lines represent load vs deflection for full depth loose saturated sand
I values are moment of inertia for pile about axis perpendicular to applied load (shown in mm4 x 108)
For HP 12 x 53
Load in KN is applied at ground surface and pile head is assumed to be 50% fixed
Thus, there probably will not be sufficient lateral load capacity with 14 vertical piles. To resolve this, it will be necessary to add more piles or batter some of the piles. Since at least twice as many piles would be required to handle the anticipated horizontal loads, battering the piles makes more sense.
Investigate battering front row of piles at 1:3 (back row of piles not battered due to lack of vertical load and potential for downdrag)
Total vertical load on front row for each of the load cases is computed by summing the individual pile loads computed above.
From Design Step P.3:
| Load Case | STR-I MAX/FIN | SER-I MAX/FIN | STR-I MIN/FIN | SER-I MIN/FIN | STR-III MAX/FIN | SER-I MAX/FIN |
|---|---|---|---|---|---|---|
| Total vertical load on front row of piles (kips) | 2119.1 | 1511.5 | 1870.8 | 1503.1 | 1730.0 | 1511.5 |
| Batter =0.333333333 | ||||||
| Available resisting force due to horizontal component of axial pile load = Batter x vertical load on front row (kips) | 706.4 | 503.8 | 623.6 | 501.0 | 576.7 | 503.8 |
| Plong =(kips) | 855.0 | 571.0 | 855.0 | 568.0 | 787.0 | 571.0 |
| Remaining force to be handled by bending of pile = Plong - available horizontal force (kips) | 148.6 | 67.2 | 231.4 | 67.0 | 210.3 | 67.2 |
| Force per pile (kips) | 10.6 | 4.8 | 16.5 | 4.8 | 15.0 | 4.8 |
Table P-12 Vertical Load on Front Row of Piles for Each Load Case
The remaining force per pile to be handled in bending is in the reasonable range thus this may be a workable configuration but it must be confirmed by interaction analysis. Thus proceed to next step with a 14 pile group with the front row battered at 3V:1H.
Design Step P.12 - Evaluate Pile Head Fixity
The performance of the pile group and the resulting pile stresses are greatly influenced by the degree to which piles are fixed against rotation at the pile head. This fixity is provided by the pile cap and is a function of the embedment of the pile into the cap, the geometry of the pile group, the stiffness of the pile cap, and the deflection. Each of these is evaluated below.
S10.7.3.8
Embedment
Research has shown that a pile needs to be embedded 2-3 times its diameter into the pile cap in order to develop full fixity. These piles will be embedded the minimum of 1 foot since the thickness of the pile cap is expected to be only 2.5 feet. Embedding the piles 2 feet into a 2.5 thick cap places the tops of the piles near the top layer of reinforcing and increases the probability of the pile punching through the top of the cap under load. Thus full pile head fixity will likely not develop regardless of other factors.
S10.7.1.5
Group geometry
In the transverse direction, there will be 7 rows of piles that when deflected force the pile cap to remain level. This condition will result in full fixity of the pile head pending evaluation of other factors. In the longitudinal direction there will be only 2 rows of piles which should be sufficient to enforce fixity pending evaluation of other factors. However, if the front row of piles is battered and the back row of piles is left vertical, the pile cap will tend to rotate backwards as it deflects. This could conceivably result in a moment applied to the pile heads greater than that required to fix the head (i.e. greater than 100% fixity) This backwards rotation of the pile cap is accounted for in the group analysis so it does not need to be considered here.
Pile cap stiffness
Flexing of the pile cap due to applied loads and moments tends to reduce the fixity at the head of the pile. In this case the pile cap is expected to be relatively thin so this effect becomes important. The stiffness of the pile cap is accounted for in the group interaction analysis so this does not effect the evaluation of fixity.
Deflection
The fixity of a pile is reduced at large deflections due to cracking of the concrete at the bottom of the pile cap. For the vertical pile group deflections are expected to be large but for the battered group deflections are likely to be small.
Conclusion
Since the group analysis will account for the group geometry and the stiffness of the pile cap, the remaining factors of embedment and deflection need to be accounted for. Both of these indicate that pile head fixity is likely to be somewhere between 25 and 75% with the higher values for the battered group. To be conservative, the group will be analyzed with 0 and 100% fixity to determine the critical conditions for pile stress (usually 100% fixity) and deflection (0 % fixity)
Design Step P.13 - Perform Pile Soil Interaction Analysis
Group interaction analysis will be performed using the computer program FB-Pier developed by FHWA, FloridaDOT and University of Florida. This program is available from the Bridge Software Institute associated with the University of Florida. Version 3 of the program is used in this example.
S10.7.3.11
In order to properly use the program, a few additional soil and pile cap properties need to be established. These are:
1) The location and thickness of the abutment stem. This controls the relative stiffness of the pile cap.
2) The location and distribution of applied loads.
3) The axial response of the soil and rock (T-z and Q-z)
4) The lateral response of soil (P-y)
5) The torsional response of the soil and rock (T- q)
6) Other miscellaneous considerations
Each is evaluated below:
Location and thickness of stem.
Previous analysis has developed a preliminary stem thickness of 3.5 feet located 2.75' from the toe of the footing. The stem is 15' tall thus the footing will be thickened to 15' in this zone as shown on the sketch below:
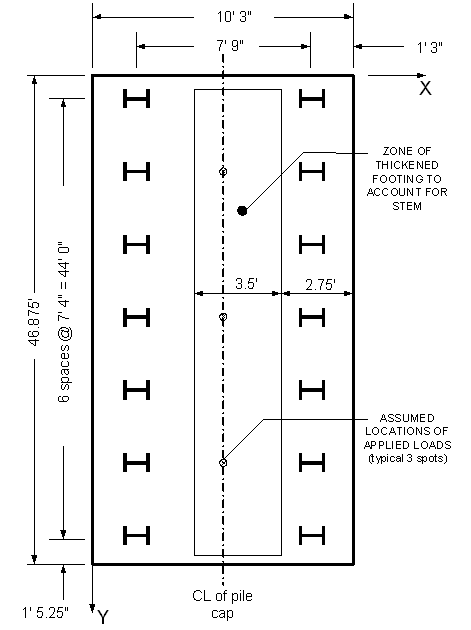
Figure P-12 Location and Thickness of Stem
Location of applied loads
The loads as supplied so far were resolved to a point at the center of the footing and the bottom of the pile cap. The loads actually consist of numerous loads due to earth pressure, superstructure, self weight etc. that are distributed over the proposed structure. To simplify the analysis, only the pile cap will be modeled in FB-Pier. The supplied loads will be divided by 3 and applied to the pile cap at 3 locations along the length of the stem at the centerline of the pile group. Since the cap will be modeled as a membrane element at an elevation that corresponds to the base of the pile cap and the loads were supplied at the base of the pile cap, no additional changes to the supplied loads and moments are required. The assumed locations of the applied loads are shown above.
The magnitude of loads and moments are computed from those provided in section P.3 as shown below. The terminology and sign convention has been converted to that used in FB-Pier. The coordinate system used is a right handed system as shown in the sketch above with Z pointing down.
Note the loads at each point provided below are in Kip-FT units
| LIMIT STATE | FB-Pier Load Case | Fz (K) | My (K-FT) | Mx (K-FT) | Fx (K) | Fy (K) |
|---|---|---|---|---|---|---|
| STR-I MAX/FIN | 1 | 751.0 | -2564.3 | 0.0 | 285.0 | 0.0 |
| SER-I MAX/FIN | 2 | 597.0 | -1591.3 | 54.0 | 190.3 | 3.3 |
| STR-I MIN/FIN | 3 | 620.0 | -2430.3 | 0.0 | 285.0 | 0.0 |
| SER-I MIN/FIN | 4 | 597.0 | -1569.7 | 54.0 | 189.3 | 3.3 |
| STR-III MAX/FIN | 5 | 605.0 | -2124.7 | 169.3 | 262.3 | 12.3 |
| SER-I MAX/FIN | 6 | 597.0 | -1591.3 | 54.0 | 190.3 | 3.3 |
Table P-13 Loads for Each Limit State
The axial response of the soil and rock (T-z and Q-z)
Since the piles will be point bearing, friction response of the soil will be small compared to the point resistance and can be ignored. However, for cases that develop tension in the piles, frictional response of the soil will be the only thing that resists that tension. Therefore, two cases will need to be run, one with the frictional response set to zero by specifying a custom T-z curve and the second with the friction response set to the default for a driven pile in granular material.
Point response of the pile bearing on rock (Q-z) will be a function of the elastic properties of the rock and will be input as a custom Q-z curve as defined below.
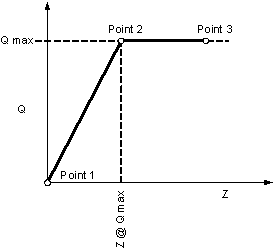
Figure P-13 Q-z Curve
From Design Step P.7:
![]()
z @ Qmax is estimated using the methods for a drilled shaft socketed in rock.
z @ Qmax: 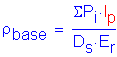
CEquation 10.8.3.5-2
where:
Load at top of socket:
Since
CFigure 10.8.3.5-1
Influence coefficient (DIM):
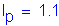
Diameter of socket, for HP12 pile:
Modulus of elasticity of rock mass (TSF):
where:
Modulus modification ratio based on RQD, from Design Step P.1:
CFigure 10.8.3.5-3
Modulus of elasticity of intact rock, from Design Step P.1:
Thus,
![]()
CEquation 10.8.3.5-3
![]()
and:
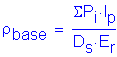
![]()
![]()
Thus Q-z curve is defined by the following points
(refer to the sketch above for location of the points)
| Point | Q (kips) | z (IN) |
|---|---|---|
| 1 | 0 | 0.00 |
| 2 | 1985 | 0.12 |
| 3 | 1985 | 2.00 |
Table P-14 Q-z Curve Points
The lateral response of soil and rock (P-y)
For Soil, use built in P-y curve for sand (Reese) with
![]() o
o
![]()
![]()
Assume pile will drive into top weathered portion of rock estimated to be 1' thick.
The embedment of the pile into the rock will provide some amount of lateral restraint at the pile tip. The response of the rock will be relatively stiff compared to the soil. To simulate this response, use the built in P-y curve for a stiff clay above the water table since the shape of this curve is closest to actual rock response. Input parameters for this curve are estimated below:
Shear strength
Average qu, Design Step P.1:
Arbitrarily reduce to 10% of this value to account for weathering
10% of Average qu:
Shear strength, 1/2 qu:
Say shear strength:
Unit weight
Average Υ, Design Step P.1:
Strain at 50% ultimate shear strength (ε50)
This is based on experience with similar rocks or it can be determined from the results of the unconfined tests if stress and strain data was recorded during the test.
The torsional response of the soil and rock (T- q)
From Design Step P.1:
o
From Design Step P.10:
Note: Τmax calculated as the total skin friction calculated by DRIVEN analysis divided by surface area of pile embedded in soil during that analysis. This represents an average value along the length of the pile and is not truly representative of the torsional response of the pile. However, a more sophisticated analysis is not warranted since torsional response of the piles will be minimal in a multi pile group that is not subject to significant eccentric horizontal loading.
Miscellaneous other considerations
Modulus of elasticity of concrete in pile cap
Assume pile cap is constructed of concrete with ![]()
![]()
Then, modulus of elasticity of concrete
![]()
![]()
![]()
![]()
Poisson's ratio for concrete
Assume:
![]()
Pile lengths
Since top of rock is level and front row of piles is battered, front row of piles will be slightly longer than back row so set up front row as a second pile set.
Back row of piles:
Batter
(3V:1H)
Front row of piles:
Group Interaction
c-c spacing in direction of load:
c-c spacing in direction perpendicular to load:
The C-C spacing in direction of load is almost 8D and since it gets larger with depth due to the batter on the front row, there should be no horizontal group effects.
The C-C spacing in both directions is greater than 3D thus there should be no horizontal or vertical group effects.
Therefore set all group interaction factors to 1.0
Deflection measurement location
See previous design sections for geometry of abutment
The critical point for evaluation of deflections is at the bearing locations which are 17.5 feet above the bottom of the pile cap as modeled. To account for pile cap rotations in the computation of displacement, add a 17.5' tall column to the center of the footing. This is a stick only with nominal properties and sees no load due to the way the problem is modeled.
Results of Analyses
Four runs were made with different combinations of pile head fixity and considering frictional resistance from the soil. These are expected to bracket the extremes of behavior of the pile group. The results of the four runs are summarized in the table below.
The results in Table P-15 are summarized from the FB-Pier Output files
| Run # | Units | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Pile head condition | Fixed | Pinned | Fixed | Pinned | |
| Soil Friction | No | No | Yes | Yes | |
| Strength Limit State | |||||
| Maximum Axial load | Kip | 340 | 332 | 340 | 332 |
| Pile number and LC | Pile 8 LC1 | Pile 8 LC1 | Pile 8 LC1 | Pile 8 LC1 | |
| Maximum Tension | Kip | 0.06 | 1.45 | 15.3 | 2.25 |
| Pile number and LC | Pile 7 LC3 | Pile 7 LC3 | Pile 1 LC3 | Pile 13 LC3 | |
| Max combined load | |||||
| Axial | kip | 288 | 289 | 336 | 290 |
| M2 | kip-ft | 0 | 0 | 0 | 0 |
| M3 | kip-ft | 107 | 100 | 26 | 97 |
| Pile number and LC | Pile 8 LC3 | Pile 8 LC3 | Pile 6 LC1 | Pile 8 LC3 | |
| Depth | FT | 8 | 8 | 0 | 8 |
| Max V2 | Kips | 18.1 | 18.2 | 15.9 | 18.1 |
| Pile number and LC | Pile 7 LC3 | Pile 7 LC3 | Pile 7 LC3 | Pile 7 LC3 | |
| Max V3 | Kips | 3.4 | 3 | 3.3 | 3 |
| Pile number and LC | Pile 2 LC5 | Pile 13 LC5 | Pile 2 LC5 | Pile 13 LC5 | |
| Service Limit State | |||||
| Max X Displacement | IN | 0.481 | 0.489 | 0.46 | 0.474 |
| Max Vertical Displacement | IN | 0.133 | 0.122 | 0.123 | 0.108 |
| Load Case | LC6 | LC6 | LC6 | LC6 | |
| Max Y displacement | IN | 0.02 | 0.053 | 0.02 | 0.053 |
| Load Case | LC6 | LC6 | LC6 | LC6 | |
Table P-15 Results
View of model
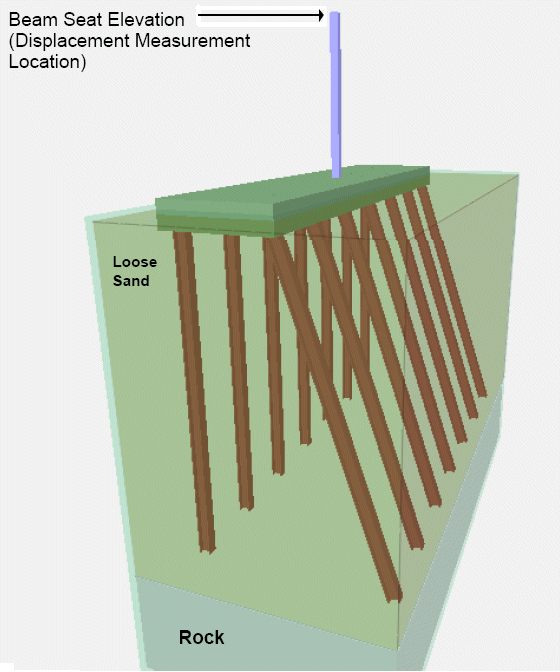
Figure P-14 Model
Design Step P.14 - Check Geotechnical Axial Capacity
From the FB-Pier analyses, and Design Step P.13:
Max factored axial pile load:
Max factored tension pile load:
These occurred when the pile was assumed to be fully fixed in the pile cap and when soil friction was considered
The maximum factored geotechnical axial resistance, from Design Step P.10 is:
![]() (Controlled by drivability considerations)
(Controlled by drivability considerations)
The ultimate geotechnical tension resistance can be taken as the reverse of what was computed in step P.10 using driven
S10.7.3.7.2
![]()
Factored resistance: ![]()
where:
The ultimate shaft resistance in compression:
Resistance factor for tension loading:
STable 10.5.5-2
The computer program Driven employs the Nordlund method to compute shaft friction. No resistance factor is provided for the Nordlund method applied to granular soils but the method is similar to the b method and has similar reliability.
thus:
The geotechnical resistance in compression and tension exceeds the maximum factored compressive and tensile pile loads. Thus geotechnical resistance is adequate.
S10.5.3
Design Step P.15 - Check Structural Axial Capacity (in lower portion of pile)
From the FB-Pier analyses, and Design Step P.13:
Max factored axial pile load:
Max factored tension pile load:
These occurred when the pile was assumed to be fully fixed in the pile cap and when soil friction was considered
The maximum factored structural axial resistance in the lower portion of the pile, from Design Step P.10 is:
![]()
This is also applicable to tension.
The factored structural resistance far exceeds the maximum factored loads. Thus, the piles are adequately sized to transmit axial loads.
Design Step P.16 - Check Structural Axial Capacity in Combined Bending and Axial Load (upper portion of pile)
The equation to use to evaluate combined axial load and bending is determined by the ratio:
![]()
S6.9.2.2
where:
Axial compressive load:
Factored compressive resistance:
where:
From Design Step P.10:
For combined axial and bending (undamaged section of pile):
S6.5.4.2
so:
![]()
![]()
From Design Step P.13, maximum combined loadings range from:
![]() to
to ![]()
so:
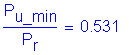 to
to 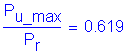
Since these are both greater than 0.2
The combined loading must satisfy:
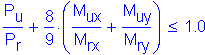
SEquation 6.9.2.2-2
where:
are as defined above
Factored flexural moment about the x axis, from Design Step P.13:
Factored flexural moment about the y axis, from Design Step P.13:
Factored flexural resistance about the x axis:
Factored flexural resistance about the y axis:
Flexural resistance is: ![]()
S6.10.4-1
where:
The resistance factor for combined bending and axial load in piles:
S6.5.4.2
Mn is computed in accordance with the provisions of Section 6.12.
 |
Deep Foundations Surrounded by Soil In most cases where deep foundations are completely surrounded by soil, lateral support from even the weakest soil is sufficient such that the unbraced length can be considered zero. When the unbraced length is zero, the buckling considerations of section 6.10.4 generally result in no reduction of the ultimate bending stress and Mn=the plastic moment or Mn=fy*Z where Z is the plastic section modulus. Note that the plastic section modulus is used in LRFD design, not the elastic section modulus. The evaluation of buckling criteria on the following pages is presented for completeness. |
For bending about the x axis, the provisions of Section 6.10.4 apply as follows:
S6.12.2.2.1
Criteria from Section 6.10.4.1.2:
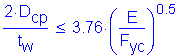
SEquation 6.10.4.1.2-1
for HP 12 x 53 Grade 50 piles: ![]()
![]()
From Design Step P.5: ![]()
Modulus of Elasticity: ![]()
As in Design Step P.10: ![]()
Check:
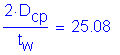
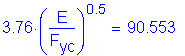
Therefore:
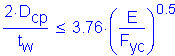 is satisfied.
is satisfied.
Criteria from Section 6.10.4.1.3:
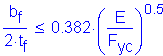
SEquation 6.10.4.1.3-1
where:
![]()
![]()
Check:
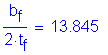
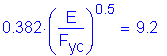
Therefore:
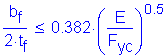 NOT SATISFIED
NOT SATISFIED
Proceed with criteria of Section 6.10.4.1.4:
Criteria from Section 6.10.4.1.4:
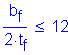
Check:
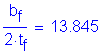 >
> ![]() Condition is NOT SATISFIED
Condition is NOT SATISFIED
However, this criteria is intended for welded sections to prevent distortion of the flange during welding. Since this is a rolled section, this practical limit does not apply.
S6.10.4.1.4
Therefore proceed to bracing requirements of Section 6.10.4.1.9:
Criteria from Section 6.10.4.1.9:
The pile is laterally braced along its entire length by the adjacent soil thus the unbraced length (Lb) is zero and this condition is always satisfied.
S6.10.4.1.9
Proceed to noncompact section flange flexural resistance of Section 6.10.4.2.4
For compression flange: ![]()
SEquation 6.10.4.2.4a-2
where:
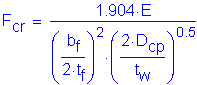
![]()
but:
![]() cannot exceed
cannot exceed ![]()
so:
![]()
and:
Hybrid factor as specified in Section 6.10.4.3.1 for a homogeneous section:
![]()
S6.10.4.3.1a
Load shedding factor specified in Section 6.10.4.3.2:
![]()
Check:
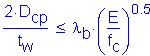
SEquation 6.10.4.3.2a-1
where:
Since ![]()
![]()
Compressive stress in the flange due to factored loads. Since this condition will be critical when fc is the largest, assume fc = the maximum possible stress which is the yield stress of the steel.
![]()
![]()
Check:
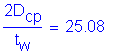
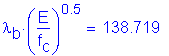
Therefore:
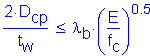 is satisfied
is satisfied
thus:
![]()
so:
![]()
![]()
For tension flange: ![]()
SEquation 6.10.4.2b-1
where:
![]()
![]() for tension flange
for tension flange
S6.10.4.3.2b
![]()
Therefore:
![]()
![]()
Since the nominal plastic stress in all components of the pile is equal to
the yield stress, The nominal moment capacity may be computed as the plastic moment.
![]()
![]()
where:
The plastic section modulus about the x axis, from Design Step P.5:
![]()
so:
![]()
![]()
![]()
![]()
![]()
For bending about the y axis, provisions of Section 6.12.2.2.1 apply.
![]()
SEquation 6.12.2.2.1-1
![]()
![]()
From Design Step P.5.
![]()
![]()
![]()
Check using alternate method from Section C6.12.2.2.1 ![]()
CEquation 6.12.2.2.1
where:
The elastic section modulus about the y axis: ![]()
![]()
![]() close to that computed above
close to that computed above
Use ![]()
![]()
The factored moment resistances are now determined as: ![]()
SEquation 6.10.4-1
so:
![]()
![]()
and:
![]()
![]()
From the maximum combined loads from Design Step P.13:
The interaction equation is now applied to the maximum combined loading conditions determined in the 4 FB-Pier analyses as follows
![]()
SEquation 6.9.2.2-2
| FB-Pier Run # | Pu (kips) | Mux (kip-ft) | Muy (kip-ft) | Results of interaction equation | ||
|---|---|---|---|---|---|---|
| 1 | 288 | 107 | 0 | 0.84 | ||
| 2 | 289 | 100 | 0 | 0.82 | ||
| 3 | 336 | 26 | 0 | 0.69 | ||
| 4 | 290 | 97 | 0 | 0.81 | ||
Table P-16 Results of Interaction Equation
All conditions satisfy the interaction equation thus piles are acceptable under combined loading.
Design Step P.17 - Check Structural Shear Capacity
 |
Pile Capacity The capacity of the pile section to resist the maximum applied shear force is usually not critical for steel pile sections placed in groups such that high overturning moments are not required to be resisted by the pile. However, in foundation systems consisting of concrete foundation elements arranged as a single element or a single row of elements supporting a tall laterally loaded pier or supporting a column subject to a large eccentric vertical load, this can become the controlling criteria. It is checked here for completeness. |
The nominal shear capacity of the pile section is computed as for an unstiffened
web of a steel beam. ![]()
SEquation 6.10.7.2-1
where: ![]()
SEquation 6.10.7.2-2
![]()
From Design Step P.5
![]()
![]()
so:
![]()
![]()
and
C is determined based on criteria in Section 6.10.7.3.3a with k = 5
compute: ![]()
compute: 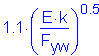
SEquation 6.10.7.3.3a-5
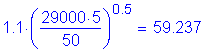
Check: ![]()
thus: ![]()
so:
![]()
![]()
Factored resistance: ![]()
Resistance factor for shear: ![]()
S6.5.4.2
so:
![]()
![]()
From Design Step P.13, the maximum factored shear in any pile in the FB-Pier analysis was 18.2 K.
Thus, piles are acceptable for shear.
Design Step P.18 - Check Maximum Horizontal and Vertical Deflection of Pile Group at Beam Seats Using Service Load Case
Displacements were determined in the interaction analysis with FB-Pier
It can be seen from the results that the horizontal displacements at the beam seat elevation are slightly higher for the cases of pinned head piles. This is expected and the difference is usually much greater. In this case, the battered piles in the front row resist the majority of the lateral load so pile head fixity is not critical to performance of the foundation system.
From Design Step P.13:
The maximum horizontal deflection observed is ![]()
The maximum vertical deflection observed is ![]()
The structural engineer has determined allowable deflections as
The maximum horizontal deflection allowed is ![]()
S10.7.2.2
The maximum vertical deflection allowed is ![]()
S10.7.2.3.1
Thus deflections are within tolerances and Service limit states are satisfied.
S10.7.2.4 and S10.7.2.3.1
Design Step P.19 - Additional Miscellaneous Design Issues
Downdrag
S10.7.1.4
As indicated in step P.1 elastic settlement of the loose sand will occur after construction of the pile foundation and abutment as the backfill behind the abutment is placed and the approach embankment is constructed.
Compute Settlement for consideration of Downdrag
Figure P-15 shows the location and dimensions of rectangles used to simulate approach embankment loading. The 150' length was arbitrarily selected as representative of the length beyond which additional influence from the approach embankment at the abutment location is not significant. The final approach embankment geometry relative to existing grade may decrease or increase this value. However, use of 150' is considered a reasonable upper bound.
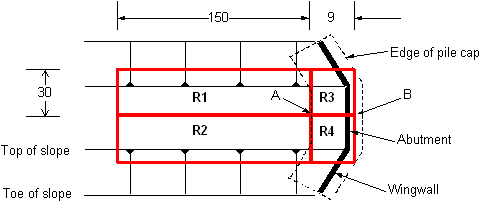
Figure P-15 Plan View of Approach Embankment
Compute settlement at back edge of pile cap (Point A)
Depth of layer = ![]()
![]()
![]()
h of fill = ![]()
Υ of fill = ![]()
![]()
At point A include influence from R1 and R2
![]()
![]()
![]()
Note: Influence factors from NAVFAC DM7 are used here because they allow proper consideration of a layer of finite thickness underlain by a rigid base. The influence values in AASHTO assume an infinite elastic halfspace. Also note that the influence values in NAVFAC are for use with a different form of the elastic settlement equation than the one contained in AASHTO. The influence values published in NAVFAC must be used with the settlement equation in NAVFAC as presented below.
From NAVFAC DM7.1-213:
![]() for ν = 0.33
for ν = 0.33
NAVFAC DM7.1-211:
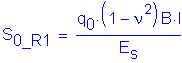
![]()
For two rectangles:
![]()
![]()
Compute settlement at front row of piles (Point B)
To simulate this case; the corner of R1 and R2 are shifted forward to be coincident with point B, and the settlement due to the approach fill weight will be equal to that computed for Point A. However, the weight of the approach embankment above the heel of the footing will be supported by the pile foundation and will not contribute to elastic settlement. Thus the settlement at point B can be computed by subtracting the influence of rectangles R3 and R4 from the settlement computed for rectangles R1 and R2 alone.
Contribution of R3 and R4 only
![]()
![]()
![]()
From NAVFAC DM7.1-213
![]() for ν = 0.33
for ν = 0.33
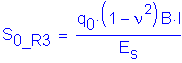
![]()
![]() (for two rectangles)
(for two rectangles) ![]()
![]()
![]()
This is not sufficient settlement to mobilize downdrag on the front row of piles as per FHWA HI-96-033, Section 9.9.1
Sufficient settlement to mobilize downdrag forces is expected at the back row of piles but not at the front row of piles. This is because the loading producing the settlement is transmitted to the soil starting at the back edge of the footing. Evaluation of downdrag loads is required for the back row of piles but not the front row. Since the back row of piles is lightly loaded and vertical, they can probably handle the downdrag load without any special details. To verify this, the following conservative approach is used.
The maximum possible downdrag force per pile is equal to the ultimate tension capacity computed in step P.14. This conservatively assumes that downdrag is mobilized along the entire length of the pile and is not reduced by the live load portion of the axial load.
S10.7.1.4
and
C10.7.1.4
![]()
Since downdrag is a load, it is factored in accordance with Section 3.4.1-2.
STable 3.4.1-2
![]() (maximum)
(maximum)
Maximum factored drag load per pile
![]()
![]()
From FB-Pier analysis, the maximum factored Axial load on back row of piles is 23.85 K.
Note: higher loads were observed for service load cases.
If the factored downdrag is added to the maximum observed factored pile load on the back row, the total factored load is:
This is well below the factored resistance computed in Design Step P.10
Thus downdrag loads can be safely supported by the back row of piles as designed.
Battered Piles
S10.7.1.6
This bridge is not in seismic zones 3 or 4 thus battered piles are OK
No downdrag is expected at the front row of piles thus batter of front row is OK
Protection Against Deterioration
S10.7.1.8
Design Step P.1 determined soils and ground water were non corrosive thus no special protection scheme or sacrificial steel is required.
Uplift and Pile to Pile Cap Connection
S10.7.1.9
The FB-Pier analysis showed some of the piles in the back row to be in tension under some of the strength limit states. None of the service limit states showed piles in tension.
 |
Pile Capacity To adequately transfer the tension load from the pile to the pile cap, a special connection detail involving reinforcing passing through a hole in the pile web or shear studs would be normally required. |
However, The cases run in FB-Pier that used no skin friction effectively simulate the case of a pile pulling out of the bottom of the footing under tension load. Review of these runs indicate that the pile could be pulled completely out of the bottom of the footing thus design of a tension connection should be included in the design of the pile cap.
From Design Step P.13, the maximum factored tension force is
![]()
The pile cap connection should be designed to resist this force.
Evaluation of the Pile Group Design
Does Pile Foundation Meet all Applicable Criteria?
Design Steps P.14 through P.19 indicate that all the applicable criteria are met
Is Pile System Optimized?
Determine if the pile system could be improved to reduce cost
Maximum factored axial load is:
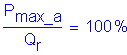 of resistance
of resistance
Maximum factored combined load is:
From Table P.16, the maximum results of the interaction equation yields: 84% of resistance
Some of the front row are not fully loaded due to flexing of the relatively thin pile cap but the front row can be considered optimized.
The back row of piles is severely under utilized for the loads investigated.
However, load cases in which the longitudinal forces are reversed will result in higher loads on the back row of piles. These loads will not exceed the loads on the front row since some longitudinal loads can not be reversed (earth pressure). Still, it may be possible to eliminate every other pile in the back row and still meet all criteria.
A brief evaluation of this possibility using FB-Pier indicates that removing 3 piles from the back row could cause the combined bending and axial stress in the front row of piles to exceed that allowed by the interaction equation. This is because elimination of the piles in the back row causes more of the horizontal loads to be absorbed by the front piles which produces higher bending moments in these piles.
Based on the above, the design is optimized to the greatest extent practical
Summary of Final Design Recommendations
Final Pile Cap Layout
All Piles are HP 12 x 53 Grade 50
All dimensions shown at bottom of pile cap
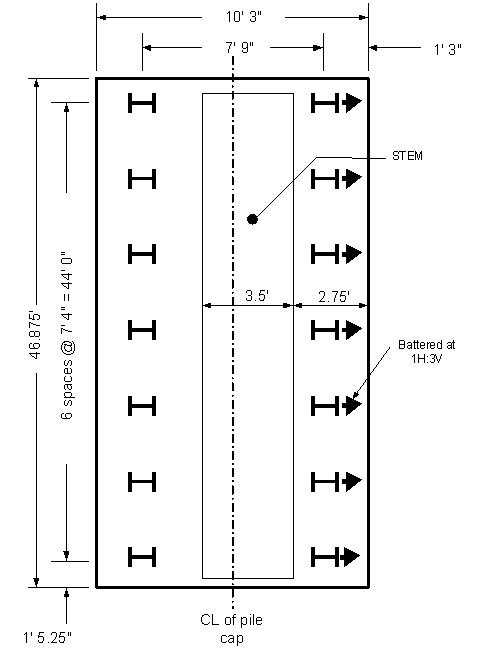
Figure P-16 Final Pile Cap Layout
Design considerations for design of pile cap
Piles to be embedded 1' into pile cap
Piles to have bar through web or shear stud to transfer 15 Kip tension load to cap
For structural design of the cap, the factored axial load per pile is summarized in tables below.
From FB-Pier File FHWA_bat_fix_noskin.out
CASE: Fixed Pile Heads No Skin Friction
| FB-Pier Load Case | LC1 | LC2 | LC3 | LC4 | LC5 | LC6 |
|---|---|---|---|---|---|---|
| Limit State | STR-I MAX/FIN | SER-I MAX/FIN | STR-I MIN/FIN | SER-I MIN/FIN | STR-III MAX/FIN | SER-I MAX/FIN |
| Pile Number | ||||||
| 1 | -6.9 | -35.0 | 0.1 | -36.1 | 0.0 | -35.0 |
| 2 | -315.3 | -221.5 | -273.3 | -220.3 | -275.2 | -221.5 |
| 3 | -12.7 | -40.1 | 0.1 | -41.3 | 0.0 | -40.1 |
| 4 | -330.5 | -232.2 | -287.1 | -230.9 | -284.7 | -232.2 |
| 5 | -15.4 | -41.9 | 0.1 | -43.1 | 0.0 | -41.9 |
| 6 | -336.1 | -235.9 | -292.4 | -234.7 | -286.3 | -235.9 |
| 7 | -17.0 | -42.8 | 0.1 | -44.0 | 0.0 | -42.8 |
| 8 | -339.9 | -238.6 | -292.4 | -237.3 | -286.2 | -238.6 |
| 9 | -15.3 | -40.7 | 0.1 | -41.9 | 0.0 | -40.7 |
| 10 | -335.4 | -234.9 | -288.4 | -233.7 | -279.3 | -234.9 |
| 11 | -12.6 | -37.8 | 0.1 | -38.9 | 0.0 | -37.8 |
| 12 | -330.7 | -230.8 | -287.8 | -229.5 | -272.6 | -230.8 |
| 13 | -6.7 | -31.3 | 0.1 | -32.4 | 0.0 | -31.3 |
| 14 | -315.6 | -219.3 | -274.1 | -218.1 | -256.4 | -219.3 |
Table P-17 Factored Axial Load per Pile Fixed Pile Heads - No Skin Friction
From FB-Pier File FHWA_bat_pin_noskin.out
CASE: Pinned Pile Heads No Skin Friction
| FB-Pier Load Case | LC1 | LC2 | LC3 | LC4 | LC5 | LC6 |
|---|---|---|---|---|---|---|
| Limit State | STR-I MAX/FIN | SER-I MAX/FIN | STR-I MIN/FIN | SER-I MIN/FIN | STR-III MAX/FIN | SER-I MAX/FIN |
| Pile Number | ||||||
| 1 | -13.7 | -36.6 | 1.4 | -37.8 | -14.6 | -36.6 |
| 2 | -308.4 | -219.2 | -274.5 | -218.0 | -254.3 | -219.2 |
| 3 | -19.5 | -41.7 | 1.4 | -42.9 | -16.8 | -41.7 |
| 4 | -323.8 | -230.3 | -288.4 | -229.0 | -267.1 | -230.3 |
| 5 | -22.2 | -43.4 | 1.4 | -44.6 | -16.7 | -43.4 |
| 6 | -329.5 | -234.3 | -293.7 | -233.1 | -271.7 | -234.3 |
| 7 | -23.8 | -44.2 | 1.4 | -45.5 | -15.8 | -44.2 |
| 8 | -332.2 | -237.0 | -294.0 | -235.7 | -272.1 | -237.0 |
| 9 | -22.1 | -42.1 | 1.4 | -43.3 | -12.4 | -42.1 |
| 10 | -327.8 | -233.6 | -290.0 | -232.4 | -268.2 | -233.6 |
| 11 | -19.3 | -39.0 | 1.4 | -40.2 | -7.9 | -39.0 |
| 12 | -324.3 | -230.0 | -289.0 | -228.7 | -266.7 | -230.0 |
| 13 | -13.3 | -32.4 | 1.4 | -33.6 | -0.8 | -32.4 |
| 14 | -309.1 | -218.8 | -275.3 | -217.5 | -253.8 | -218.8 |
Table P-18 Factored Axial Load per Pile Pinned Pile Heads - No Skin Friction
From FB-Pier File FHWA_bat_fix_skin.out
CASE: Fixed Pile Heads Skin Friction
| FB-Pier Load Case | LC1 | LC2 | LC3 | LC4 | LC5 | LC6 |
|---|---|---|---|---|---|---|
| Limit State | STR-I MAX/FIN | SER-I MAX/FIN | STR-I MIN/FIN | SER-I MIN/FIN | STR-III MAX/FIN | SER-I MAX/FIN |
| Pile Number | ||||||
| 1 | -5.6 | -34.0 | 15.3 | -35.1 | -1.6 | -34.0 |
| 2 | -314.5 | -220.6 | -287.0 | -219.4 | -271.7 | -220.6 |
| 3 | -11.8 | -39.3 | 14.8 | -40.5 | -1.4 | -39.3 |
| 4 | -330.3 | -231.8 | -301.2 | -230.5 | -282.8 | -231.8 |
| 5 | -14.6 | -41.2 | 14.5 | -42.4 | 0.2 | -41.2 |
| 6 | -336.0 | -235.7 | -306.4 | -234.4 | -285.7 | -235.7 |
| 7 | -16.2 | -42.2 | 14.4 | -43.4 | 0.8 | -42.2 |
| 8 | -339.9 | -238.4 | -309.3 | -237.1 | -286.7 | -238.4 |
| 9 | -14.5 | -40.0 | 14.5 | -41.2 | 1.8 | -40.0 |
| 10 | -335.3 | -234.6 | -305.1 | -233.4 | -280.7 | -234.6 |
| 11 | -11.6 | -37.0 | 14.8 | -38.2 | 2.9 | -37.0 |
| 12 | -330.5 | -230.5 | -301.4 | -229.2 | -274.9 | -230.5 |
| 13 | -5.5 | -30.3 | 15.3 | -31.4 | 4.4 | -30.3 |
| 14 | -314.8 | -218.5 | -287.3 | -217.3 | -259.3 | -218.5 |
Table P-19 Factored Axial Load per Pile Fixed Pile Heads - Skin Friction
From FB-Pier File FHWA_bat_fix_skin.out
CASE: Pinned Pile Heads Skin Friction
| FB-Pier Load Case | LC1 | LC2 | LC3 | LC4 | LC5 | LC6 |
|---|---|---|---|---|---|---|
| Limit State | STR-I MAX/FIN | SER-I MAX/FIN | STR-I MIN/FIN | SER-I MIN/FIN | STR-III MAX/FIN | SER-I MAX/FIN |
| Pile Number | ||||||
| 1 | -13.3 | -36.2 | 2.1 | -37.3 | -14.3 | -36.2 |
| 2 | -307.5 | -218.0 | -274.6 | -216.8 | -254.4 | -218.0 |
| 3 | -19.5 | -41.6 | 1.4 | -42.7 | -16.7 | -41.6 |
| 4 | -323.5 | -229.6 | -289.2 | -228.3 | -267.7 | -229.6 |
| 5 | -22.3 | -43.3 | 1.1 | -44.5 | -16.7 | -43.3 |
| 6 | -329.4 | -233.8 | -294.7 | -232.5 | -272.6 | -233.8 |
| 7 | -23.9 | -44.2 | 0.9 | -45.5 | -15.9 | -44.2 |
| 8 | -332.0 | -236.4 | -295.0 | -235.1 | -273.0 | -236.4 |
| 9 | -22.1 | -42.0 | 1.1 | -43.2 | -12.5 | -42.0 |
| 10 | -327.4 | -232.9 | -290.9 | -231.6 | -268.9 | -232.9 |
| 11 | -19.2 | -38.8 | 1.5 | -40.0 | -7.9 | -38.8 |
| 12 | -324.0 | -229.3 | -289.9 | -228.0 | -267.4 | -229.3 |
| 13 | -13.0 | -32.0 | 2.2 | -33.2 | -0.7 | -32.0 |
| 14 | -308.2 | -217.6 | -275.6 | -216.3 | -253.9 | -217.6 |
Table P-20 Factored Axial Load per Pile Pined Pile Heads - Skin Friction
Absolute maximum from above: ![]()
Absolute minimum from above: ![]()
FB-Pier may be used to print out all stresses in each element of the pile cap as a check on manual methods if desired.
Notes to be placed on Final Drawing
Maximum Factored Axial Pile Load = 340K
Required Factored Axial Resistance = 340K
Piles to be driven to absolute refusal defined as a penetration resistance of 20 Blows Per Inch (BPI) using a hammer and driving system components that produces a driving stress between 37 and 45 KSI at refusal. Driving stress to be estimated using wave equation analysis of the selected hammer.
Verify capacity and driving system performance by performing stress wave measurements on a minimum of 2 piles in each substructure. One test shall be on a vertical pile and the other shall be on a battered pile.
Perform a CAPWAP analysis of each dynamically tested pile. The CAPWAP analysis shall confirm the following:
Driving stress is in the range specified above.
The ultimate pile point capacity (after subtracting modeled skin friction) is greater than:
![]()
This is based on a resistance factor (Φ) of 0.65 for piles tested dynamically.
References:
FHWA HI-96-033 Design and Construction of Driven Pile Foundations, Hannigan, P.J., Gobel, G.G, Thedean, G., Likins, G.E., and Rausche, F. for FHWA, December 1996, Volume 1 and 2
NAVFAC DM7 Design Manual 7; Volume 1 - Soil Mechanics; Volume 2 - Foundations and Earth Structures, Department of the Navy, Naval Facilities Engineering Command, May 1982.
PADOT DM4 Design Manual Part 4, Pennsylvania Department of Transportation Publication 15M, April 2000
Reese and Wang (1991) Unpublished paper presenting group efficiencies of pile groups subject to horizontal loads in diferent directions and at different spacings.
NCEER-97-0022 Proceedings of the NCEER Workshop on Evaluation of Liquefaction Resistance of Soils, Edited by T.L. Youd, I.M. Idriss. Summary Report, 1997. MCEER Publication NCEER-97-0022
| << previous | Contents |