LRFD Steel Girder SuperStructure Design Example
Pier Design Example Design Step 8
Table of Contents
Design Step 8.1 - Obtain Design Criteria
Design Step 8.2 - Select Optimum Pier Type
Design Step 8.3 - Select Preliminary Pier Dimensions
Design Step 8.4 - Compute Dead Load Effects
Design Step 8.5 - Compute Live Load Effects
Design Step 8.6 - Compute Other Load Effects
Design Step 8.7 - Analyze and Combine Force Effects
Design Step 8.8 - Design Pier Cap
Design Step 8.9 - Design Pier Column
Design Step 8.10 - Design Pier Piles
Design Step 8.11 - Design Pier Footing
Design Step 8.12 - Final Pier Schematic
Design Step 8.1 - Obtain Design Criteria
This pier design example is based on AASHTO LRFD Bridge Design Specifications (through 2002 interims). The design methods presented throughout the example are meant to be the most widely used in general bridge engineering practice.
The first design step is to identify the appropriate design criteria. This includes, but is not limited to, defining material properties, identifying relevant superstructure information, determining the required pier height, and determining the bottom of footing elevation.
Refer to Design Step 1 for introductory information about this design example. Additional information is presented about the design assumptions, methodology, and criteria for the entire bridge, including the pier.
The following units are defined for use in this design example:
![]()
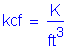
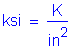
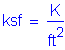
![]()
Material Properties:
Concrete density: STable 3.5.1-1 Concrete 28-day compressive strength: S5.4.2.1 CTable5.4.2.1-1 Reinforcement strength: 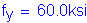
S5.4.3 Concrete 28-day compressive strength - For all components of this pier design example, 4.0 ksi is used for the 28-day compressive strength. However, per the Specifications, 2.4 ksi could be used for the pier footing.
C5.4.2.1
Reinforcing steel cover requirements (assume non-epoxy rebars):
Pier cap: 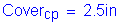
STable 5.12.3-1 Pier column: 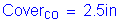
STable 5.12.3-1 Footing top cover: 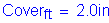
STable 5.12.3-1 Footing bottom cover: 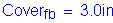
STable 5.12.3-1
Pier cap and column cover - Since no joint exists in the deck at the pier, a 2-inch cover could be used with the assumption that the pier is not subject to deicing salts. However, it is assumed here that the pier can be subjected to a deicing salt spray from nearby vehicles. Therefore, the cover is set at 2.5 inches.
STable 5.12.3-1
Footing top cover - The footing top cover is set at 2.0 inches.
STable 5.12.3-1
Footing bottom cover - Since the footing bottom is cast directly against the earth, the footing bottom cover is set at 3.0 inches.
STable 5.12.3-1
Relevant superstructure data:
Girder spacing: 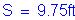
Number of girders: 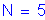
Deck overhang: 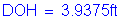
Span length: Parapet height: Deck overhang thickness: Haunch thickness: (includes top flange)
Web depth: (based on 1st trial section)
Bot. flange thickness: (maximum thickness)
Bearing height: Superstructure Depth: 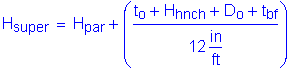
Superstructure data - The above superstructure data is important because it sets the width of the pier cap and defines the depth and length of the superstructure needed for computation of wind loads.
S3.8
Pier height - Guidance on determining the appropriate pier height can be found in the AASHTO publication A Policy on Geometric Design of Highways and Streets. It will be assumed here that adequate vertical clearance is provided given a ground line that is two feet above the top of the footing and the pier dimensions given in Design Step 8.3.
S2.3.3.2
Bottom of Footing Elevation - The bottom of footing elevation may depend on the potential for scour (not applicable in this example) and/or the geotechnical properties of the soil and/or rock. However, as a minimum, it should be at or below the frost depth for a given geographic region. In this example, it is assumed that the two feet of soil above the footing plus the footing thickness provides sufficient depth below the ground line for frost protection of the structure.
S10.6.1.2
Design Step 8.2 - Select Optimum Pier Type
Selecting the most optimal pier type depends on site conditions, cost considerations, superstructure geometry, and aesthetics. The most common pier types are single column (i.e., "hammerhead"), solid wall type, and bent type (multi-column or pile bent). For this design example, a single column (hammerhead) pier was chosen. A typical hammerhead pier is shown in Figure 8-1.
S11.2
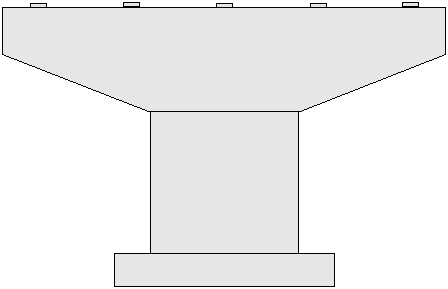
Figure 8-1 Typical Hammerhead Pier
Design Step 8.3 - Select Preliminary Pier Dimensions
Since the Specifications do not have standards regarding maximum or minimum dimensions for a pier cap, column, or footing, the designer should base the preliminary pier dimensions on state specific standards, previous designs, and past experience. The pier cap, however, must be wide enough to accommodate the bearing.
Figures 8-2 and 8-3 show the preliminary dimensions selected for this pier design example.
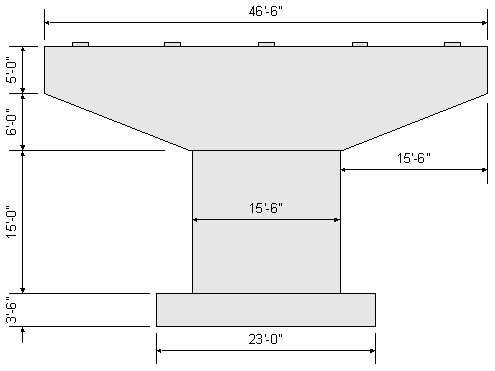
Figure 8-2 Preliminary Pier Dimensions - Front Elevation
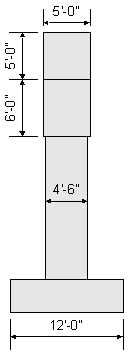
Figure 8-3 Preliminary Pier Dimensions - End Elevation
Design Step 8.4 - Compute Dead Load Effects
Once the preliminary pier dimensions are selected, the corresponding dead loads can be computed. The pier dead loads must then be combined with the superstructure dead loads. The superstructure dead loads shown below are obtained from the superstructure analysis/design software. Based on the properties defined in Design Step 3 (Steel Girder Design), any number of commercially available software programs can be used to obtain these loads. For this design example, the AASHTO Opis software was used, and the values shown below correspond to the first design iteration.
S3.5.1
Exterior girder dead load reactions (DC and DW):
![]()
![]()
Interior girder dead load reactions (DC and DW):
![]()
![]()
Pier cap dead load:
Overhang:
Interior:
Total:
Pier column dead load:
![]()
![]()
Pier footing dead load:
![]()
![]()
In addition to the above dead loads, the weight of the soil on top of the footing must be computed. The two-foot height of soil above the footing was previously defined. Assuming a unit weight of soil at 0.120 kcf :
STable 3.5.1-1
![]()
![]()
Design Step 8.5 - Compute Live Load Effects
For the pier in this design example, the maximum live load effects in the pier cap, column and footing are based on either one, two or three lanes loaded (whichever results in the worst force effect). Figure 8-4 illustrates the lane positions when three lanes are loaded.
The positioning shown in Figure 8-4 is arrived at by first determining the number of design lanes, which is the integer part of the ratio of the clear roadway width divided by 12 feet per lane. Then the lane loading, which occupies ten feet of the lane, and the HL-93 truck loading, which has a six-foot wheel spacing and a two-foot clearance to the edge of the lane, are positioned within each lane to maximize the force effects in each of the respective pier components.
S3.6.1.1.1
S3.6.1.2.1
S3.6.1.2.4
S3.6.1.3.1
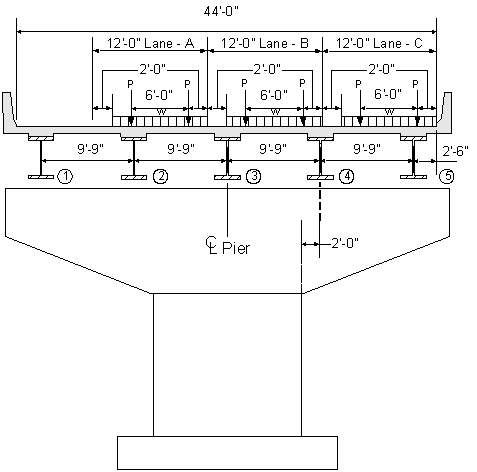
Figure 8-4 Pier Live Loading
The unfactored girder reactions for lane load and truck load are obtained from the superstructure analysis/design software. These reactions do not include dynamic load allowance and are given on a per lane basis (i.e., distribution factor = 1.0). Also, the reactions do not include the ten percent reduction permitted by the Specifications for interior pier reactions that result from longitudinally loading the superstructure with a truck pair in conjunction with lane loading. The value of these reactions from the first design iteration are as follows:
S3.6.1.3.1
![]()
![]()
Dynamic load allowance, IM ![]()
STable 3.6.2.1-1
The values of the unfactored concentrated loads which represent the girder truck load reaction per wheel line in Figure 8-4 are:
![]()
![]()
The value of the unfactored uniformly distributed load which represents the girder lane load reaction in Figure 8-4 is computed next. This load is transversely distributed over ten feet and is not subject to dynamic load allowance.
S3.6.2.1
![]()
![]()
The next step is to compute the reactions due to the above loads at each of the five bearing locations. This is generally carried out by assuming the deck is pinned (i.e., discontinuous) at the interior girder locations but continuous over the exterior girders. Solving for the reactions is then elementary. The computations for the reactions with only Lane C loaded are illustrated below as an example. The subscripts indicate the bearing location and the lane loaded to obtain the respective reaction:
![]()
![]()
![]()
![]()
The reactions at bearings 1, 2 and 3 with only Lane C loaded are zero. Calculations similar to those above yield the following live load reactions with the remaining lanes loaded (for simplicity, it is assumed that Lane B's loading is resisted entirely, and equally, by bearings 3 and 4):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Design Step 8.6 - Compute Other Load Effects
Other load effects that will be considered for this pier design include braking force, wind loads, temperature loads, and earthquake loads.
Braking Force
S3.6.4
Since expansion bearings exist at the abutments, the entire longitudinal braking force is resisted by the pier.
The braking force per lane is the greater of:
25 percent of the axle weights of the design truck or tandem
5 percent of the axle weights of the design truck plus lane load
5 percent of the axle weights of the design tandem plus lane load
The total braking force is computed based on the number of design lanes in the same direction. It is assumed in this example that this bridge is likely to become one-directional in the future. Therefore, any and all design lanes may be used to compute the governing braking force. Also, braking forces are not increased for dynamic load allowance. The calculation of the braking force for a single traffic lane follows:
S3.6.1.1.1
S3.6.2.1
25 percent of the design truck:
![]()
![]()
25 percent of the design tandem:
![]()
![]()
5 percent of the axle weights of the design truck plus lane load:
![]()
![]()
5 percent of the axle weights of the design tandem plus lane load:
![]()
![]()
Use ![]()
![]()
The Specifications state that the braking force is applied at a distance of six feet above the roadway surface. However, since the bearings are assumed incapable of transmitting longitudinal moment, the braking force will be applied at the bearing elevation (i.e., five inches above the top of the pier cap). This force may be applied in either horizontal direction (back or ahead station) to cause the maximum force effects. Additionally, the total braking force is typically assumed equally distributed among the bearings:
S3.6.4
![]()
![]()
Wind Load from Superstructure
S3.8.1.2
Prior to calculating the wind load on the superstructure, the structure must be checked for aeroelastic instability. If the span length to width or depth ratio is greater than 30, the structure is considered wind-sensitive and design wind loads should be based on wind tunnel studies.
S3.8.3
![]()
![]()
![]()
![]()
![]() OK
OK ![]() OK
OK
Since the span length to width and depth ratios are both less than 30, the structure does not need to be investigated for aeroelastic instability.
To compute the wind load on the superstructure, the area of the superstructure exposed to the wind must be defined. For this example, the exposed area is the total superstructure depth multiplied by length tributary to the pier. Due to expansion bearings at the abutment, the transverse length tributary to the pier is not the same as the longitudinal length.
S3.8.1.1
The superstructure depth includes the total depth from the top of the barrier to the bottom of the girder. Included in this depth is any haunch and/or depth due to the deck cross-slope. Once the total depth is known, the wind area can be calculated and the wind pressure applied.
The total depth was previously computed in Section 8.1 and is as follows:
![]()
For this two-span bridge example, the tributary length for wind load on the pier in the transverse direction is one-half the total length of the bridge:
![]()
![]()
In the longitudinal direction, the tributary length is the entire bridge length due to the expansion bearings at the abutments:
![]()
The transverse wind area is:
![]()
![]()
The longitudinal wind area is:
![]()
![]()
Since the superstructure is approximately 30 feet above low ground level, the design wind velocity, VB, does not have to be adjusted. Therefore:
S3.8.1.1
![]()
![]()
![]()
From this, the design wind pressure is equal to the base wind pressure:
S3.8.1.2.1
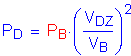
or
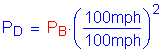
![]()
Also, the minimum transverse normal wind loading on girders must be greater than or equal to 0.30 KLF:
S3.8.1.2.1
![]()
![]() , which is greater than 0.30 klf
, which is greater than 0.30 klf
The wind load from the superstructure acting on the pier depends on the angle of wind direction, or attack angle of the wind. The attack angle is taken as measured from a line perpendicular to the girder longitudinal axis (see Figure 8-5). The base wind pressures for the superstructure for various attack angles are given in STable 3.8.1.2.2-1.
S3.8.1.2.2
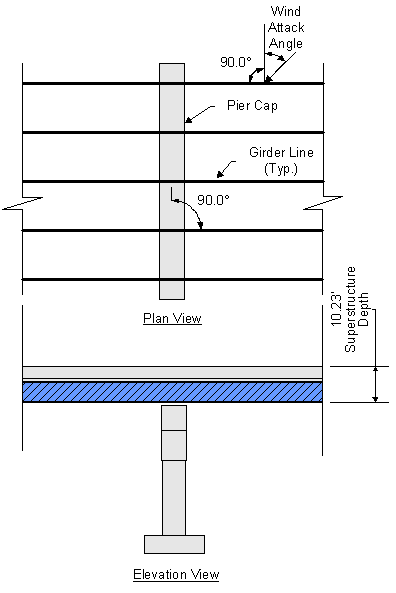
Figure 8-5 Application of Wind Load
Two wind load calculations are illustrated below for two different wind attack angles. The wind loads for all Specifications required attack angles are tabulated in Table 8-1.
For a wind attack angle of 0 degrees, the superstructure wind loads acting on the pier are:
![]()
STable 3.8.1.2.2-1
![]()
![]()
![]()
For a wind attack angle of 60 degrees, the superstructure wind loads acting on the pier are:
![]()
STable 3.8.1.2.2-1
![]()
![]()
![]()
|
Pier Design Wind Loads from Superstructure
|
|||
|
Wind Attack Angle
Degrees |
Bridge Transverse Axis
KIPS |
Bridge Longitudinal Axis
Kips |
|
|
0
|
61.38
|
0.00
|
|
|
15
|
54.01
|
14.73
|
|
|
30
|
50.33
|
29.46
|
|
|
45
|
40.51
|
39.28
|
|
|
60
|
20.87
|
46.65
|
|
Table 8-1 Pier Design Wind Loads from Superstructure for Various Wind Attack Angles
The total longitudinal wind load shown above for a given attack angle is assumed to be divided equally among the bearings. In addition, the load at each bearing is assumed to be applied at the top of the bearing (i.e., five inches above the pier cap). These assumptions are consistent with those used in determining the bearing forces due to the longitudinal braking force.
The transverse wind loads shown in Table 8-1 for a given attack angle are also assumed to be equally divided among the bearings and applied at the top of each bearing. However, as shown in Figure 8-6, the transverse load also applies a moment to the pier cap. This moment, which acts about the centerline of the pier cap, induces vertical loads at the bearings as illustrated in Figure 8-6. The computations for these vertical forces with an attack angle of zero are presented below.
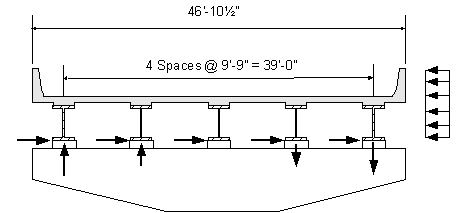
Figure 8-6 Transverse Wind Load Reactions at Pier Bearings from Wind on Superstructure
![]()
![]()
![]()
![]()
![]()
![]()
The reactions at bearings 1 and 5 are equal but opposite in direction. Similarly for bearings 2 and 4:
![]()
![]()
Finally, by inspection:
![]()
The vertical reactions at the bearings due to transverse wind on the superstructure at attack angles other than zero are computed as above using the appropriate transverse load from Table 8-1. Alternatively, the reactions for other attack angles can be obtained simply by multiplying the reactions obtained above by the ratio of the transverse load at the angle of interest to the transverse load at an attack angle of zero (i.e., 61.38K).
Vertical Wind Load
S3.8.2
The vertical (upward) wind load is calculated by multiplying a 0.020 ksf vertical wind pressure by the out-to-out bridge deck width. It is applied at the windward quarter-point of the deck only for limit states that do not include wind on live load. Also, the wind attack angle must be zero degrees for the vertical wind load to apply.
From previous definitions:
![]()
![]()
The total vertical wind load is then:
![]()
![]()
This load causes a moment about the pier centerline. The value of this moment is:
![]()
![]()
The reactions at the bearings are computed as follows:
![]()
![]()
![]()
![]()
![]()
The above computations lead to the following values:
![]()
![]() (vertically upward)
(vertically upward)
![]() (vertically upward)
(vertically upward)
![]() (vertically upward)
(vertically upward)
![]() (vertically upward)
(vertically upward)
Wind Load on Vehicles
S3.8.1.3
The representation of wind pressure acting on vehicular traffic is given by the Specifications as a uniformly distributed load. Based on the skew angle, this load can act transversely, or both transversely and longitudinally. Furthermore, this load is to be applied at a distance of six feet above the roadway surface. The magnitude of this load with a wind attack angle of zero is 0.10 klf. For wind attack angles other than zero, STable 3.8.1.3-1 gives values for the longitudinal and transverse components. For the transverse and longitudinal loadings, the total force in each respective direction is calculated by multiplying the appropriate component by the length of structure tributary to the pier. Similar to the superstructure wind loading, the longitudinal length tributary to the pier differs from the transverse length.
![]()
![]()
An example calculation is illustrated below using a wind attack angle of 30 degrees:
![]()
STable 3.8.1.3-1
![]()
![]()
STable 3.8.1.3-1
![]()
Table 8-2 contains the total transverse and longitudinal loads due to wind load on vehicular traffic at each Specifications required attack angle.
|
Design Vehicular Wind Loads
|
||
|---|---|---|
|
Wind Attack Angle
Degrees |
Bridge Transverse Axis
Kips |
Bridge Longitudinal Axis
Kips |
|
0
|
12.00
|
0.00
|
|
15
|
10.56
|
2.88
|
|
30
|
9.84
|
5.76
|
|
45
|
7.92
|
7.68
|
|
60
|
4.08
|
9.12
|
Table 8-2 Design Vehicular Wind Loads for Various Wind Attack Angles
The vehicular live loads shown in Table 8-2 are applied to the bearings in the same manner as the wind load from the superstructure. That is, the total transverse and longitudinal load is equally distributed to each bearing and applied at the the top of the bearing (five inches above the top of the pier cap). In addition, the transverse load acting six feet above the roadway applies a moment to the pier cap. This moment induces vertical reactions at the bearings. The values of these vertical reactions for a zero degree attack angle are given below. The computations for these reactions are not shown but are carried out as shown in the subsection "Wind Load from Superstructure." The only difference is that the moment arm used for calculating the moment is equal to (Hsuper - Hpar + 6.0 feet).
![]()
![]()
![]()
Wind Load on Substructure
S3.8.1.2.3
The Specifications state that the wind loads acting directly on substructure units shall be calculated from a base wind pressure of 0.040 ksf. It is interpreted herein that this pressure should be applied to the projected area of the pier that is normal to the wind direction. This is illustrated in Figure 8-7. The resulting force is then the product of 0.040 ksf and the projected area. For nonzero wind attack angles, this force is resolved into components applied to the front and end elevations of the pier, respectively. These loads act simultaneously with the superstructure wind loads.
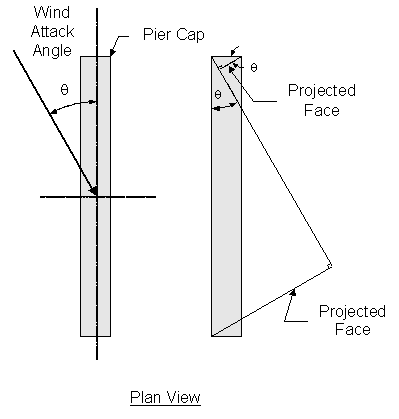
Figure 8-7 Projected Area for Wind Pressure on Pier
What follows is an example of the calculation of the wind loads acting directly on the pier for a wind attack angle of 30 degrees. For simplicity, the tapers of the pier cap overhangs will be considered solid (this is conservative and helpful for wind angles other than zero degrees). The column height exposed to wind is the distance from the ground line (which is two feet above the footing) to the bottom of the pier cap.
Component areas of the pier cap:
![]()
![]()
![]()
![]()
Projected area of pier cap:
![]()
![]()
Component areas of the pier column:
![]()
![]()
![]()
![]()
Projected area of pier column:
![]()
![]()
The total wind force is then:
![]()
![]()
The transverse and longitudinal force components are:
![]()
![]()
![]()
![]()
The point of application of these loads will be the centroid of the loaded area of each face, respectively. This point will be approximated here as 17 feet above the top of the footing for both the transverse and longitudinal directions.
The wind attack angles for the pier must match the wind attack angles used for the superstructure. Table 8-3 shows the pier wind loads for the various attack angles.
|
Wind Loads Applied Directly to Pier
|
|||||
|---|---|---|---|---|---|
|
Wind Attack Angle
Degrees |
APcap
ft2 |
APcol
ft2 |
Total Wind Load
Kips |
Trans. Force
Kips |
Long. Force
Kips |
|
0
|
55.00
|
58.50
|
4.54
|
4.54
|
0.00
|
|
15
|
185.51
|
108.66
|
11.77
|
11.37
|
3.05
|
|
30
|
303.38
|
151.41
|
18.19
|
15.75
|
9.10
|
|
45
|
400.58
|
183.85
|
23.38
|
16.53
|
16.53
|
|
60
|
470.47
|
203.75
|
26.97
|
13.49
|
23.36
|
Table 8-3 Design Wind Loads Applied Directly to Pier for Various Wind Attack Angles Earthquake Load
S3.10
It is assumed in this design example that the structure is located in Seismic Zone I with an acceleration coefficient of 0.02. For Seismic Zone I, a seismic analysis is not required. However, the Specifications require a minimum design force for the check of the superstructure to substructure connection. Also, at locations of expansion bearings, a minimum bridge seat must be provided.
S4.7.4.1
S3.10.9
S4.7.4.4
Since the bearings at the pier are fixed both longitudinally and transversely, minimum bridge seat requirements for seismic loads are not applicable. Also, since the bearing design is carried out in Design Step 6, the calculations for the check of the connection will not be shown here. Therefore, the earthquake provisions as identified in the above paragraph will have no impact on the overall pier design and will not be discussed further.
Temperature Loading (Superimposed Deformations)
S3.12
In general, uniform thermal expansion and contraction of the superstructure can impose longitudinal forces on the substructure units. These forces can arise from restraint of free movement at the bearings. Additionally, the physical locations and number of substructure units can cause or influence these forces.
S3.12.2
STable 3.12.2.1-1
In this particular structure, with a single pier centered between two abutments that have identical bearing types, theoretically no force will develop at the pier from thermal movement of the superstructure. However, seldom are ideal conditions achieved in a physical structure. Therefore, it is considered good practice to include an approximate thermal loading even when theory indicates the absence of any such force.
For the purpose of this design example, a total force of 20 kips will be assumed. This force acts in the longitudinal direction of the bridge (either back or ahead station) and is equally divided among the bearings. Also, the forces at each bearing from this load will be applied at the top of the bearing (i.e., five inches above the pier cap).
![]()
![]()
![]()
![]()
![]()
Design Step 8.7 - Analyze and Combine Force Effects
The first step within this design step will be to summarize the loads acting on the pier at the bearing locations. This is done in Tables 8-4 through 8-15 shown below. Tables 8-4 through 8-8 summarize the vertical loads, Tables 8-9 through 8-12 summarize the horizontal longitudinal loads, and Tables 8-13 through 8-15 summarize the horizontal transverse loads. These loads along with the pier self-weight loads, which are shown after the tables, need to be factored and combined to obtain total design forces to be resisted in the pier cap, column and footing.
It will be noted here that loads applied due to braking and temperature can act either ahead or back station. Also, wind loads can act on either side of the structure and with positive or negative skew angles. This must be kept in mind when considering the signs of the forces in the tables below. The tables assume a particular direction for illustration only.
|
Superstructure Dead Load
|
Wearing Surface Dead Load
|
|||
|---|---|---|---|---|
|
Bearing
|
Variable Name
|
Reaction (Kips)
|
Variable Name
|
Reaction (Kips)
|
|
1
|
RDCE
|
253.70
|
RDWE
|
39.20
|
|
2
|
RDCI
|
269.10
|
RDWI
|
39.20
|
|
3
|
RDCI
|
269.10
|
RDWI
|
39.20
|
|
4
|
RDCI
|
269.10
|
RDWI
|
39.20
|
|
5
|
RDCE
|
253.70
|
RDWE
|
39.20
|
Table 8-4 Unfactored Vertical Bearing Reactions from Superstructure Dead Load
|
Vehicular Live Load **
|
||||||
|---|---|---|---|---|---|---|
|
Lane A
|
Lane B
|
Lane C
|
||||
|
Bearing
|
Variable Name
|
Reaction (Kips)
|
Variable Name
|
Reaction (Kips)
|
Variable Name
|
Reaction (Kips)
|
|
1
|
R1_a
|
4.19
|
R1_b
|
0.00
|
R1_c
|
0.00
|
|
2
|
R2_a
|
161.59
|
R2_b
|
0.00
|
R2_c
|
0.00
|
|
3
|
R3_a
|
70.96
|
R3_b
|
118.36
|
R3_c
|
0.00
|
|
4
|
R4_a
|
0.00
|
R4_b
|
118.36
|
R4_c
|
60.69
|
|
5
|
R5_a
|
0.00
|
R5_b
|
0.00
|
R5_c
|
176.00
|
**Note: Live load reactions include impact on truck loading.
Table 8-5 Unfactored Vertical Bearing Reactions from Live Load
|
Reactions from Transverse Wind Load on Superstructure (kips)
|
|||||
|---|---|---|---|---|---|
|
Wind Attack Angle (degrees)
|
|||||
|
Bearing
|
0
|
15
|
30
|
45
|
60
|
|
1
|
6.44
|
5.67
|
5.28
|
4.25
|
2.19
|
|
2
|
3.22
|
2.83
|
2.64
|
2.12
|
1.09
|
|
3
|
0.00
|
0.00
|
0.00
|
0.00
|
0.00
|
|
4
|
-3.22
|
-2.83
|
-2.64
|
-2.12
|
-1.09
|
|
5
|
-6.44
|
-5.67
|
-5.28
|
-4.25
|
-2.19
|
Table 8-6 Unfactored Vertical Bearing Reactions from Wind on Superstructure
|
Reactions from Transverse Wind Load on Vehicular Live Load
(kips)
|
|||||
|---|---|---|---|---|---|
|
Wind Attack Angle (degrees)
|
|||||
|
Bearing
|
0
|
15
|
30
|
45
|
60
|
|
1
|
3.13
|
2.76
|
2.57
|
2.07
|
1.07
|
|
2
|
1.57
|
1.38
|
1.28
|
1.03
|
0.53
|
|
3
|
0.00
|
0.00
|
0.00
|
0.00
|
0.00
|
|
4
|
-1.57
|
-1.38
|
-1.28
|
-1.03
|
-0.53
|
|
5
|
-3.13
|
-2.76
|
-2.57
|
-2.07
|
-1.07
|
Table 8-7 Unfactored Vertical Bearing Reactions from Wind on Live Load
|
Vertical Wind Load on Superstructure
|
||
|---|---|---|
|
Bearing
|
Variable Name
|
Reaction (Kips)
|
|
1
|
RWSvert1
|
4.63
|
|
2
|
RWSvert2
|
-8.97
|
|
3
|
RWSvert3
|
-22.56
|
|
4
|
RWSvert4
|
-36.15
|
|
5
|
RWSvert5
|
-49.75
|
Table 8-8 Unfactored Vertical Bearing Reactions from Vertical Wind on Superstructure
|
Braking Load **
|
Temperature Loading
|
|||
|---|---|---|---|---|
|
Bearing
|
Variable Name
|
Reaction (Kips)
|
Variable Name
|
Reaction (Kips)
|
|
1
|
BRKbrg
|
3.60
|
TU1
|
4.00
|
|
2
|
BRKbrg
|
3.60
|
TU2
|
4.00
|
|
3
|
BRKbrg
|
3.60
|
TU3
|
4.00
|
|
4
|
BRKbrg
|
3.60
|
TU4
|
4.00
|
|
5
|
BRKbrg
|
3.60
|
TU5
|
4.00
|
**Note: Values shown are for a single lane loaded
Table 8-9 Unfactored Horizontal Longitudinal Bearing Reactions from Braking and Temperature
|
Longitudinal Wind Loads from Superstructure (kips)
|
|||||
|---|---|---|---|---|---|
|
Wind Attack Angle (degrees)
|
|||||
|
Bearing
|
0
|
15
|
30
|
45
|
60
|
|
1
|
0.00
|
2.95
|
5.89
|
7.86
|
9.33
|
|
2
|
0.00
|
2.95
|
5.89
|
7.86
|
9.33
|
|
3
|
0.00
|
2.95
|
5.89
|
7.86
|
9.33
|
|
4
|
0.00
|
2.95
|
5.89
|
7.86
|
9.33
|
|
5
|
0.00
|
2.95
|
5.89
|
7.86
|
9.33
|
|
Total =
|
0.00
|
14.73
|
29.46
|
39.28
|
46.65
|
Table 8-10 Unfactored Horizontal Longitudinal Bearing Reactions from Wind on Superstructure
|
Longitudinal Wind Loads from Vehicular Live Load (kips)
|
|||||
|---|---|---|---|---|---|
|
Wind Attack Angle (degrees)
|
|||||
|
Bearing
|
0
|
15
|
30
|
45
|
60
|
|
1
|
0.00
|
0.58
|
1.15
|
1.54
|
1.82
|
|
2
|
0.00
|
0.58
|
1.15
|
1.54
|
1.82
|
|
3
|
0.00
|
0.58
|
1.15
|
1.54
|
1.82
|
|
4
|
0.00
|
0.58
|
1.15
|
1.54
|
1.82
|
|
5
|
0.00
|
0.58
|
1.15
|
1.54
|
1.82
|
|
Total =
|
0.00
|
2.88
|
5.76
|
7.68
|
9.12
|
Table 8-11 Unfactored Horizontal Longitudinal Bearing Reactions from Wind on Live Load
|
Longitudinal Substructure Wind Loads Applied Directly to Pier
(kips)
|
||||
|---|---|---|---|---|
|
Wind Attack Angle (degrees)
|
||||
|
0
|
15
|
30
|
45
|
60
|
|
0.00
|
3.05
|
9.10
|
16.53
|
23.36
|
Table 8-12 Unfactored Horizontal Longitudinal Loads from Wind Directly on Pier
|
Transverse Wind Loads from Superstructure
|
|||||
|---|---|---|---|---|---|
|
Wind Attack Angle
|
|||||
|
Bearing
|
0
|
15
|
30
|
45
|
60
|
|
1
|
12.28
|
10.80
|
10.07
|
8.10
|
4.17
|
|
2
|
12.28
|
10.80
|
10.07
|
8.10
|
4.17
|
|
3
|
12.28
|
10.80
|
10.07
|
8.10
|
4.17
|
|
4
|
12.28
|
10.80
|
10.07
|
8.10
|
4.17
|
|
5
|
12.28
|
10.80
|
10.07
|
8.10
|
4.17
|
|
Total =
|
61.38
|
54.01
|
50.33
|
40.51
|
20.87
|
Table 8-13 Unfactored Horizontal Transverse Bearing Reactions from Wind on Superstructure
|
Transverse Wind Loads from Vehicular Live Load (kips)
|
|||||
|---|---|---|---|---|---|
|
Wind Attack Angle (degrees)
|
|||||
|
Bearing
|
0
|
15
|
30
|
45
|
60
|
|
1
|
2.40
|
2.11
|
1.97
|
1.58
|
0.82
|
|
2
|
2.40
|
2.11
|
1.97
|
1.58
|
0.82
|
|
3
|
2.40
|
2.11
|
1.97
|
1.58
|
0.82
|
|
4
|
2.40
|
2.11
|
1.97
|
1.58
|
0.82
|
|
5
|
2.40
|
2.11
|
1.97
|
1.58
|
0.82
|
|
Total =
|
12.00
|
10.56
|
9.84
|
7.92
|
4.08
|
Table 8-14 Unfactored Horizontal Transverse Bearing Reactions from Wind on Live Load
|
Transverse Substructure Wind Loads Applied Directly to Pier
(kips)
|
||||
|---|---|---|---|---|
|
Wind Attack Angle (degrees)
|
||||
|
0
|
15
|
30
|
45
|
60
|
|
4.54
|
11.37
|
15.75
|
16.53
|
13.49
|
Table 8-15 Unfactored Horizontal Transverse Loads from Wind Directly on Pier
In addition to all the loads tabulated above, the pier self-weight must be considered when determining the final design forces. Additionally for the footing and pile designs, the weight of the earth on top of the footing must be considered. These loads were previously calculated and are shown below:
![]()
![]()
![]()
![]()
In the AASHTO LRFD design philosophy, the applied loads are factored by statistically calibrated load factors. In addition to these factors, one must be aware of two additional sets of factors which may further modify the applied loads.
STable 3.4.1-1
STable 3.4.1-2
The first set of additional factors applies to all force effects and are represented by the Greek letter η (eta) in the Specifications. These factors are related to the ductility, redundancy, and operational importance of the structure. A single, combined eta is required for every structure. These factors and their application are discussed in detail in Design Step 1.1. In this design example, all eta factors are taken equal to one.
S1.3.2.1
The other set of factors mentioned in the first paragraph above applies only to the live load force effects and are dependent upon the number of loaded lanes. These factors are termed multiple presence factors by the Specifications. These factors for this bridge are shown as follows:
STable 3.6.1.1.2-1
Multiple presence factor, m (1 lane)
Multiple presence factor, m (2 lanes)
Multiple presence factor, m (3 lanes)
Table 8-16 contains the applicable limit states and corresponding load factors that will be used for this pier design. Limit states not shown either do not control the design or are not applicable. The load factors shown in Table 8-16 are the standard load factors assigned by the Specifications and are exclusive of multiple presence and eta factors.
It is important to note here that the maximum load factors shown in Table 8-16 for uniform temperature loading (TU) apply only for deformations, and the minimum load factors apply for all other effects. Since the force effects from the uniform temperature loading are considered in this pier design, the minimum load factors will be used.
S3.4.1
|
Load Factors
|
||||||||
|---|---|---|---|---|---|---|---|---|
|
Strength I
|
Strength III
|
Strength V
|
Service I
|
|||||
|
Loads
|
γmax
|
γmin
|
γmax
|
γmin
|
γmax
|
γmin
|
γmax
|
γmin
|
|
DC
|
1.25
|
0.90
|
1.25
|
0.90
|
1.25
|
0.90
|
1.00
|
1.00
|
|
DW
|
1.50
|
0.65
|
1.50
|
0.65
|
1.50
|
0.65
|
1.00
|
1.00
|
|
LL
|
1.75
|
1.75
|
---
|
---
|
1.35
|
1.35
|
1.00
|
1.00
|
|
BR
|
1.75
|
1.75
|
---
|
---
|
1.35
|
1.35
|
1.00
|
1.00
|
|
TU
|
1.20
|
0.50
|
1.20
|
0.50
|
1.20
|
0.50
|
1.20
|
1.00
|
|
WS
|
---
|
---
|
1.40
|
1.40
|
0.40
|
0.40
|
0.30
|
0.30
|
|
WL
|
---
|
---
|
---
|
---
|
1.00
|
1.00
|
1.00
|
1.00
|
|
EV
|
1.35
|
1.00
|
1.35
|
1.00
|
1.35
|
1.00
|
1.00
|
1.00
|
Table 8-16 Load Factors and Applicable Pier Limit States
STable 3.4.1-1
STable 3.4.1-2
The loads discussed and tabulated previously can now be factored by the appropriate load factors and combined to determine the governing limit states in the pier cap, column, footing and piles. For this design example, the governing limit states for the pier components were determined from a commercially available pier design computer program. Design calculations will be carried out for the governing limit states only.
Pier Cap Force Effects
The controlling limit states for the design of the pier cap are Strength I (for moment, shear and torsion) and Service I ( for crack control). The critical design location is where the cap meets the column, or 15.5 feet from the end of the cap. This is the location of maximum moment, shear, and torsion. The reactions at the two outermost bearings (numbered 4 and 5 in Figure 8-4), along with the self-weight of the cap overhang, cause the force effects at the critical section. In the following calculations, note that the number of lanes loaded to achieve the maximum moment is different than that used to obtain the maximum shear and torsion.
For Strength I, the factored vertical and horizontal forces at the bearings and corresponding force effects at the critical section are shown below. Also shown are the moment arms to the critical section.
Flexure from vertical loads (reference Tables 8-4 and 8-5):
![]()
![]()
![]() (see Figure 8-4)
(see Figure 8-4)
![]()
![]()
![]()

![]()
Shear from vertical loads (reference Tables 8-4 and 8-5):
![]()
![]()
![]()
![]()
![]()
![]()
Torsion from horizontal loads (reference Table 8-9):
![]()
![]()
![]()
![]()
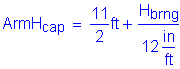
![]()
![]()
![]()
The applied torsion would be larger than the value just calculated if the vertical loads at the bearings are not coincident with the centerline of the pier cap. Some state agencies mandate a minimum eccentricity to account for this possibility. However, AASHTO does not. Therefore, no eccentricity of vertical loads is considered in this design example.
For Service I, the factored vertical forces at the bearings and corresponding force effects at the critical section are shown next. First, variables for transverse wind load on the structure and on the live load with an attack angle of zero degrees will be defined. Force effects from vertical wind load on the structure are not applicable since the Service I limit state includes wind on live load.
S3.8.2
![]()
![]()
![]()
![]()
Flexure from vertical loads (reference Tables 8-4 and 8-5):
![]()
![]()
![]() (see Figure 8-4)
(see Figure 8-4)
![]()
![]()
![]()

![]()
Pier Column Force Effects
The controlling limit states for the design of the pier column are Strength I (for biaxial bending with axial load), Strength III (for transverse shear) and Strength V (for longitudinal shear). The critical design location is where the column meets the footing, or at the column base. The governing force effects for Strength I are achieved by excluding the future wearing surface, applying minimum load factors on the structure dead load, and loading only Lane B and Lane C with live load. Transverse and longitudinal shears are maximized with wind attack angles of zero and 60 degrees, respectively.
For Strength I, the factored vertical forces and corresponding moments at the critical section are shown below.
Axial force (reference Tables 8-4 and 8-5):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Transverse moment (reference Table 8-5):
![]()
![]()
![]()
![]()
Longitudinal moment (reference Table 8-9):
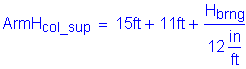
![]()

![]()
For Strength III, the factored transverse shear in the column is:
![]()
![]()
![]()
![]()
For Strength V, the factored longitudinal shear in the column is (reference Table 8-9):
![]()
![]()
![]()
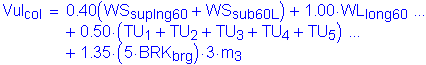
![]()
Pier Pile Force Effects
The foundation system for the pier is a reinforced concrete footing on steel H-piles. The force effects in the piles cannot be determined without a pile layout. The pile layout depends upon the pile capacity and affects the footing design. The pile layout used for this pier foundation is shown in Design Step 8.10 (Figure 8-11).
Based on the pile layout shown in Figure 8-11, the controlling limit states for the pile design are Strength I (for maximum pile load), Strength III (for minimum pile load), and Strength V (for maximum horizontal loading of the pile group).
The force effects in the piles for the above-mentioned limit states are not given. The reason for this is discussed in Design Step 8.10.
Pier Footing Force Effects
The controlling limit states for the design of the pier footing are Strength I (for flexure, punching shear at the column, and punching shear at the maximum loaded pile), Strength IV (for one-way shear), and Service I ( for crack control). There is not a single critical design location in the footing where all of the force effects just mentioned are checked. Rather, the force effects act at different locations in the footing and must be checked at their respective locations. For example, the punching shear checks are carried out using critical perimeters around the column and maximum loaded pile, while the flexure and one-way shear checks are carried out on a vertical face of the footing either parallel or perpendicular to the bridge longitudinal axis.
The Strength I limit state controls for the punching shear check at the column. The factored axial load and corresponding factored biaxial moments at the base of the column are obtained in a manner similar to that for the Strength I force effects in the pier column. However, in this case the future wearing surface is now included, maximum factors are applied to all the dead load components, and all three lanes are loaded with live load. This results in the following bottom of column forces:
![]()
![]()
![]()
Factored force effects for the remaining limit states discussed above are not shown. The reason for this is discussed in Design Step 8.11.
Design Step 8.8 - Design Pier Cap
Prior to carrying out the actual design of the pier cap, a brief discussion is in order regarding the design philosophy that will be used for the design of the structural components of this pier.
When a structural member meets the definition of a deep component, the Specifications recommends, although does not mandate, that a strut-and-tie model be used to determine force effects and required reinforcing. Specifications Commentary C5.6.3.1 indicates that a strut-and-tie model properly accounts for nonlinear strain distribution, nonuniform shear distribution, and the mechanical interaction of Vu, Tu and Mu. Use of strut-and-tie models for the design of reinforced concrete members is new to the LRFD Specification.
S5.2
S5.6.3.1
Traditionally, piers have been designed using conventional methods of strength of materials regardless of member dimensions. In this approach, it is assumed that longitudinal strains vary linearly over the depth of the member and the shear distribution remains uniform. Furthermore, separate designs are carried out for Vu and Mu at different locations along the member.
C5.6.3.1
For the purpose of this design example, all structural components, regardless of dimensions, will be designed in accordance with the conventional strength of materials assumptions described above. This approach is currently standard engineering practice.
The design of the pier cap will now proceed.
As stated in Design Step 8.7, the critical section in the pier cap is where the cap meets the column, or 15.5' from the end of the cap. The governing force effects and their corresponding limit states were determined to be:
Strength I
![]()
![]()
![]()
Service I
![]()
A preliminary estimate of the required section size and reinforcement is shown in Figure 8-8.
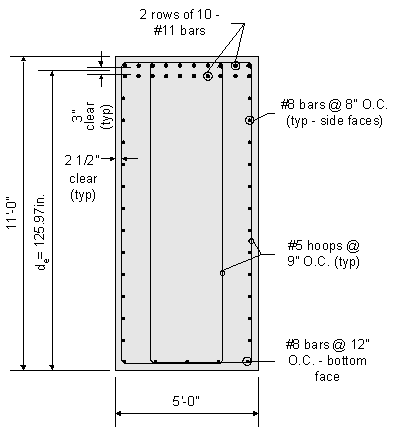
Figure 8-8 Preliminary Pier Cap Design
Design for Flexure (Strength I)
Assume #11 bars:
![]()
![]()
![]()
The minimum reinforcement requirements will be calculated for the cap. The tensile reinforcement provided must be enough to develop a factored flexural resistance at least equal to the lesser of 1.2 times the cracking strength or 1.33 times the factored moment from the applicable strength load combinations.
S5.7.3.3.2
The cracking strength is calculated as follows:
![]()
S5.4.2.6
![]()
![]()
![]()
![]()
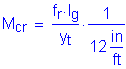
![]()
![]()
By inspection, the applied moment from the Strength I limit state exceeds 120 percent of the cracking moment. Therefore, providing steel sufficient to resist the applied moment automatically satisfies the minimum reinforcement check.
The effective depth (de) of the section shown in Figure 8-8 is computed as follows:
![]()
![]()
![]()
Solve for the required amount of reinforcing steel, as follows:
![]()
S5.5.4.2.1
![]()
![]()
![]()
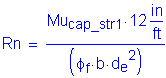
![]()
![]()
![]()
The above two equations are derived formulas that can be found in most reinforced concrete textbooks.
![]()
![]()
The area of steel provided is:
![]()
![]()
![]() OK
OK
The reinforcement area provided must now be checked to ensure that the section is not overreinforced:
S5.7.3.3.1
![]()
![]()
![]()
![]()
![]()
S5.7.2.2
![]()
![]()
S5.7.2.2
![]() where
where ![]()
S5.7.3.3.1
![]() OK
OK
Design for Flexure (Service I)
The control of cracking by distribution of reinforcement must be satisfied.
S5.7.3.4
Since this design example assumes that the pier cap will be exposed to deicing salts, use:
![]()
The distance from the extreme tension fiber to the center of the closest bar, using a maximum cover dimension of 2 inches, is:
![]()
![]()
The area of concrete having the same centroid as the principal tensile reinforcement and bounded by the surfaces of the cross-section and a straight line parallel to the neutral axis, divided by the number of bars, is:
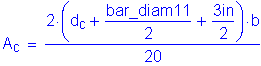
![]()
The equation that gives the allowable reinforcement service load stress for crack control is:
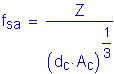 where
where ![]()
S5.7.3.4
![]()
![]()
Use ![]()
![]()
S5.4.3.2
![]()
SEquation C5.4.2.4-1
![]()
![]() Use
Use ![]()
The factored service moment in the cap is:
![]()
To solve for the actual stress in the reinforcement, the distance from the neutral axis to the centroid of the reinforcement (see Figure 8-9) and the transformed moment of inertia must be computed:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
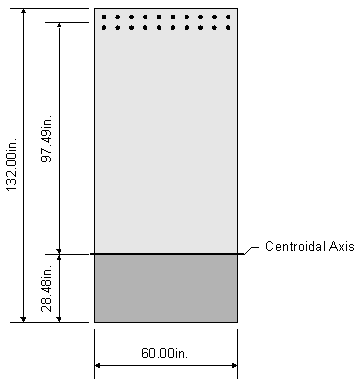
Figure 8-9 Pier Cap Under Service Loads
Once kde is known, the transformed moment of inertia can be computed:
![]()
![]()
![]()
![]()
Now, the actual stress in the reinforcement is computed:
![]()
![]()
![]()

![]()
![]()
![]() OK
OK
Design for Flexure (Skin Reinforcement)
S5.7.3.4
In addition to the above check for crack control, additional longitudinal steel must be provided along the side faces of concrete members deeper than three feet. This additional steel is referred to in the Specifications as longitudinal skin reinforcement. This is also a crack control check. However, this check is carried out using the effective depth (de) and the required longitudinal tension steel in place of specific applied factored loads.
Figure 8-8 shows longitudinal skin reinforcement (#8 bars spaced at 8" on center) over the entire depth of the pier cap at the critical section. The Specifications require this steel only over a distance de/2 from the nearest flexural tension reinforcement. However, the reinforcing bar arrangement shown in Figure 8-8 is considered good engineering practice. This includes the placement of reinforcing steel along the bottom face of the pier cap as well, which some state agencies mandate.
The calculations shown below are for the critical section in the pier cap. The skin reinforcement necessary at this section is adequate for the entire pier cap.
![]()
![]()
![]()
![]() and
and ![]()
SEquation 5.7.3.4-4
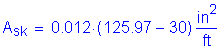
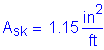 (each side face)
(each side face)
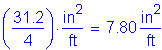
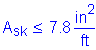 OK
OK
Spacing of the skin reinforcement:
![]()
![]()
Verify that #8 bars at 8" on center is adequate:
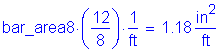
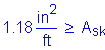 OK
OK
Design for Shear and Torsion (Strength I)
S5.8
The shear and torsion force effects were computed previously and are:
![]()
![]()
The presence of torsion affects the total required amount of both longitudinal and transverse reinforcing steel. However, if the applied torsion is less than one-quarter of the factored torsional cracking moment, then the Specifications allow the applied torsion to be ignored. This computation is shown as follows:
S5.8.2.1
![]()
S5.5.4.2.1
![]()
![]()
![]()
![]()
![]()
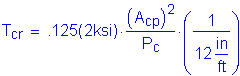
![]()
![]()
![]()
Based on the above check, torsion will be neglected and will not be discussed further. The shear check of the critical cap section will now proceed.
The nominal shear resistance of the critical section is a combination of the nominal resistance of the concrete and the nominal resistance of the steel. This value is then compared to a computed upper-bound value and the lesser of the two controls. These calculations are illustrated below:
S5.8.3.3
![]()
![]()
![]()
S5.8.2.9
![]()
![]()
![]()
S5.8.3.4.1
The nominal concrete shear strength is:
![]()
![]()
S5.8.3.3
![]()
Note that unless one-half of the product of Vc and the phi-factor for shear is greater than Vu, then transverse reinforcement must be provided. Therefore, when Vc is less than Vu, as in this case, transverse reinforcement is automatically required.
S5.8.2.4
The nominal steel shear strength is (using vertical stirrups, theta equal to 45 degrees):
![]() (4 legs of #5 bars)
(4 legs of #5 bars)
![]()
S5.8.3.3
![]()
![]()
The nominal shear strength of the critical section is the lesser of the following two values:
![]()
![]() (controls)
(controls)
S5.8.3.3
![]()
![]()
Define Vn as follows:
![]()
![]()
The factored shear resistance is:
![]()
S5.5.4.2.1
![]()
![]()
![]() OK
OK
The shear check is not complete until the provided transverse steel is compared to the Specifications requirements regarding minimum quantity and maximum spacing.
Minimum quantity required:
S5.8.2.5
![]()
![]()
![]()
![]() OK
OK
Maximum spacing allowed:
S5.8.2.7
![]()
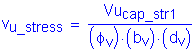
S5.8.2.9
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() OK
OK
Design Step 8.9 - Design Pier Column
As stated in Design Step 8.7, the critical section in the pier column is where the column meets the footing, or at the column base. The governing force effects and their corresponding limit states were determined to be:
Strength I
![]()
![]()
![]()
Strength III
![]()
Strength V
![]()
A preliminary estimate of the required section size and reinforcement is shown in Figure 8-10.
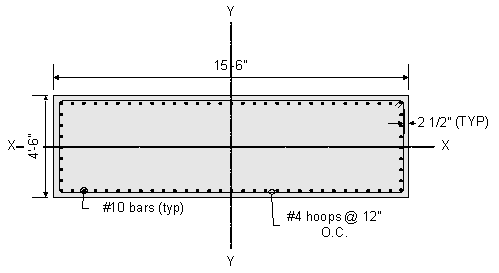
Figure 8-10 Preliminary Pier Column Design
Design for Axial Load and Biaxial Bending (Strength I):
S5.7.4
The preliminary column reinforcing is show in Figure 8-10 and corresponds to #10 bars equally spaced around the column perimeter. The Specifications prescribes limits (both maximum and minimum) on the amount of reinforcing steel in a column. These checks are performed on the preliminary column as follows:
S5.7.4.2
![]()
![]()
![]()
![]()
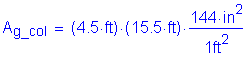
![]()
![]()
![]() OK
OK
![]()
![]() OK
OK
The column slenderness ratio (Klu/r) about each axis of the column is computed below in order to assess slenderness effects. Note that the Specifications only permit the following approximate evaluation of slenderness effects when the slenderness ratio is below 100.
S5.7.4.3
S5.7.4.1
For this pier, the unbraced lengths (lux,luy) used in computing the slenderness ratio about each axis is the full pier height. This is the height from the top of the footing to the top of the pier cap (26 feet). The effective length factors, Kx and Ky, are both taken equal to 2.1. This assumes that the superstructure has no effect on restraining the pier from buckling. In essence, the pier is considered a free-standing cantilever.
CTable4.6.2.5-1
For simplicity in the calculations that follow, let lu=lux=luy and Kcol=Kx=Ky. This is conservative for the transverse direction for this structure, and the designer may select a lower value. The radius of gyration (r) about each axis can then be computed as follows:
![]()
![]()
![]()
![]()
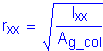
![]()
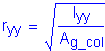
![]()
The slenderness ratio for each axis now follows:
![]()
![]()
![]()
![]() OK
OK
![]()
![]() OK
OK
The Specifications permits slenderness effects to be ignored when the slenderness ratio is less than 22 for members not braced against sidesway. It is assumed in this example that the pier is not braced against sidesway in either its longitudinal or transverse directions. Therefore, slenderness will be considered for the pier longitudinal direction only (i.e., about the "X-X" axis).
S5.7.4.3
In computing the amplification factor that is applied to the longitudinal moment, which is the end result of the slenderness effect, the column stiffness (EI) about the "X-X" axis must be defined. In doing so, the ratio of the maximum factored moment due to permanent load to the maximum factored moment due to total load must be identified (βd).
S4.5.3.2.2b
S5.7.4.3
From Design Step 8.7, it can be seen that the only force effects contributing to the longitudinal moment are the live load braking force and the temperature force. Neither of these are permanent or long-term loads. Therefore, βd is taken equal to zero for this design.
The column stiffness is taken as the greater of the following two calculations:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (controls)
(controls)
The final parameter necessary for the calculation of the amplification factor is the phi-factor for compression. This value is defined as follows:
S5.5.4.2.1
![]()
It is worth noting at this point that when axial load is present in addition to flexure, the Specifications permit the value of phi to be increased linearly to the value for flexure (0.90) as the factored axial load decreases from ten percent of the gross concrete strength to zero. However, certain equations in the Specification still require the use of the phi factor for axial compression (0.75) even when the increase just described is permitted. Therefore, for the sake of clarity in this example, if phi may be increased it will be labeled separately from Φaxial identified above.
S5.5.4.2.1
![]()
![]()
Since the factored axial load in the column is less than ten percent of the gross concrete strength, the phi-factor will be modified and separately labeled as follows:
![]()
![]()
The longitudinal moment magnification factor will now be calculated as follows:
S4.5.3.2.2b
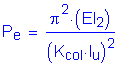
![]()
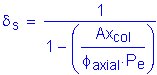
![]()
The final design forces at the base of the column for the Strength I limit state will be redefined as follows:
![]()
![]()
![]()
![]()
![]()
![]()
The assessment of the resistance of a compression member with biaxial flexure for strength limit states is dependent upon the magnitude of the factored axial load. This value determines which of two equations provided by the Specification are used.
S5.7.4.5
If the factored axial load is less than ten percent of the gross concrete strength multiplied by the phi-factor for compression members (Φaxial), then the Specifications require that a linear interaction equation for only the moments is satisfied (SEquation 5.7.4.5-3). Otherwise, an axial load resistance (Prxy) is computed based on the reciprocal load method (SEquation 5.7.4.5-1). In this method, axial resistances of the column are computed (using ΦLow_axial if applicable) with each moment acting separately (i.e., Prx with Mux, Pry with Muy). These are used along with the theoretical maximum possible axial resistance (Po multiplied by Φaxial) to obtain the factored axial resistance of the biaxially loaded column.
Regardless of which of the two equations mentioned in the above paragraph controls, commercially available software is generally used to obtain the moment and axial load resistances.
For this pier design, the procedure as discussed above is carried out as follows:
![]()
![]()
Therefore, SEquation 5.7.4.5-3 will be used.
![]()
![]()
![]()
![]()
![]()
![]() OK
OK
The factored flexural resistances shown above, Mrx and Mry, were obtained by the use of commercial software. These values are the flexural capacities about each respective axis assuming that no axial load is present. Consistent with this, the phi-factor for flexure (0.90) was used in obtaining the factored resistance from the factored nominal strength.
Although the column has a fairly large excess flexural capacity, a more optimal design will not be pursued per the discussion following the column shear check.
Design for Shear (Strength III and Strength V)
S5.8
The maximum factored transverse and longitudinal shear forces were derived in Design Step 8.7 and are as follows:
![]() (Strength III)
(Strength III)
![]() (Strength V)
(Strength V)
These maximum shear forces do not act concurrently. Although a factored longitudinal shear force is present in Strength III and a factored transverse shear force is present in Strength V, they both are small relative to their concurrent factored shear. Therefore, separate shear designs can be carried out for the longitudinal and transverse directions using only the maximum shear force in that direction.
For the pier column of this example, the maximum factored shear in either direction is less than one-half of the factored resistance of the concrete. Therefore, shear reinforcement is not required. This is demonstrated for the transverse direction as follows:
S5.8.2.4
![]()
![]()
S5.8.3.3
![]()
S5.8.2.9
![]()
The above calculation for dv is simple to use for columns and generally results in a conservative estimate of the shear capacity.
![]()
![]()
S5.8.3.4.1
The nominal concrete shear strength is:
![]()
![]()
S5.8.3.3
![]()
The nominal shear strength of the column is the lesser of the following two values:
![]()
![]() (controls)
(controls)
S5.8.3.3
![]()
![]()
Define Vn as follows:
![]()
The factored shear resistance is:
![]()
S5.5.4.2.1
![]()
S5.8.2.1
![]()
![]()
![]() OK
OK
It has just been demonstrated that transverse steel is not required to resist the applied factored shear forces. However, transverse confinement steel in the form of hoops, ties or spirals is required for compression members. In general, the transverse steel requirements for shear and confinement must both be satisfied per the Specifications.
S5.7.4.6
S5.10.6
It is worth noting that although the preceding design checks for shear and flexure show the column to be overdesigned, a more optimal column size will not be pursued. The reason for this is twofold: First, in this design example, the requirements of the pier cap dictate the column dimensions (a reduction in the column width will increase the moment in the pier cap, while good engineering practice generally prescribes a column thickness 6 to 12 inches less than that of the pier cap). Secondly, a short, squat column such as the column in this design example generally has a relatively large excess capacity even when only minimally reinforced.
Transfer of Force at Base of Column
S5.13.3.8
The provisions for the transfer of forces and moments from the column to the footing are new to the AASHTO LRFD Specifications. Although similar provisions have existed in the ACI Building Code for some time, these provisions are absent from the AASHTO Standard Specifications. In general, standard engineering practice for bridge piers automatically satisfies most, if not all, of these requirements.
In this design example, and consistent with standard engineering practice, all steel reinforcing bars in the column extend into, and are developed, in the footing (see Figure 8-13). This automatically satisfies the following requirements for reinforcement across the interface of the column and footing: A minimum reinforcement area of 0.5 percent of the gross area of the supported member, a minimum of four bars, and any tensile force must be resisted by the reinforcement. Additionally, with all of the column reinforcement extended into the footing, along with the fact that the column and footing have the same compressive strength, a bearing check at the base of the column and the top of the footing is not applicable.
In addition to the above, the Specifications requires that the transfer of lateral forces from the pier to the footing be in accordance with the shear-transfer provisions of S5.8.4. With the standard detailing practices for bridge piers previously mentioned (i.e., all column reinforcement extended and developed in the footing), along with identical design compressive strengths for the column and footing, this requirement is generally satisfied. However, for the sake of completeness, this check will be carried out as follows:
![]()
![]()
S5.8.4.1
![]()
![]()
![]()
![]()
S5.8.4.2
![]()
![]()
![]()
![]()
![]()
S5.5.4.2.1
The nominal shear-friction capacity is the smallest of the following three equations (conservatively ignore permanent axial compression):
S5.8.4.1
![]()
![]()
![]()
![]()
![]()
![]()
Define the nominal shear-friction capacity as follows:
![]()
![]()
The maximum applied shear was previously identified from the Strength V limit state:
![]()
It then follows:
![]()
![]() OK
OK
As can be seen, a large excess capacity exists for this check. This is partially due to the fact that the column itself is overdesigned in general (this was discussed previously). However, the horizontal forces generally encountered with common bridges are typically small relative to the shear-friction capacity of the column (assuming all reinforcing bars are extended into the footing). In addition, the presence of a shear-key, along with the permanent axial compression from the bridge dead load, further increase the shear-friction capacity at the column/footing interface beyond that shown above. This may account for the absence of this check in both the Standard Specifications and in standard practice.
 |
Transfer of Force at Column Base |
Design Step 8.10 - Design Pier Piles
The foundation system for the pier is a reinforced concrete footing on steel H-piles. The force effects in the piles cannot be determined without a pile layout. The pile layout depends upon the pile capacity and affects the footing design. The pile layout used for this pier foundation is shown in Figure 8-11.
S10.7
Based on the given pile layout, the controlling limit states for the pile design were given in Design Step 8.7. However, pile loads were not provided. The reason for this is that the pile design will not be performed in this design step. The abutment foundation system, discussed in Design Step 7, is identical to that of the pier, and the pile design procedure is carried out in its entirety there. Although individual pile loads may vary between the abutment and the pier, the design procedure is similar. The pile layout shown in Figure 8-11 is used only to demonstrate the aspects of the footing design that are unique to the pier. This is discussed in the next design step.
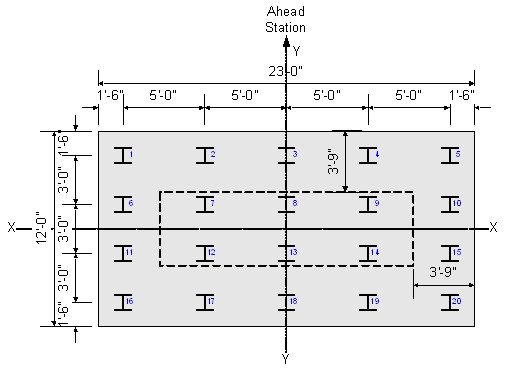
Figure 8-11 Pier Pile Layout
Design Step 8.11 - Design Pier Footing
In Design Step 8.7, the governing limit states were identified for the design of the pier footing. However, the factored force effects were only given for the Strength I check of punching shear at the column. The reason for this is that most of the design checks for the pier footing are performed similarly to those of the abutment footing in Design Step 7. Therefore, only the aspects of the footing design that are unique to the pier footing will be discussed in this design step. This includes the punching (or two-way) shear check at the column and a brief discussion regarding estimating the applied factored shear and moment per foot width of the footing when adjacent pile loads differ.
The factored force effects from Design Step 8.7 for the punching shear check at the column are:
![]()
![]()
![]()
It should be noted that in Design Step 8.5, the live load reactions at the bearings include dynamic load allowance on the truck loads. These live load force effects are part of the factored axial load and transverse moment shown above. However, the Specifications do not require dynamic load allowance for foundation components that are entirely below ground level. Therefore, the resulting pile loads will be somewhat larger (by about four percent) than necessary for the following design check. For the sake of clarity and simplicity in Design Step 8.5, a separate set of live load reactions with dynamic load allowance excluded was not provided.
S3.6.2.1
The longitudinal moment given above must be magnified to account for slenderness of the column (see Design Step 8.9). The computed magnification factor and final factored forces are:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
With the applied factored loads determined, the next step in the column punching shear check is to define the critical perimeter, bo. The Specifications require that this perimeter be minimized, but need not be closer than dv/2 to the perimeter of the concentrated load area. In this case, the concentrated load area is the area of the column on the footing as seen in plan.
S5.13.3.6.1
The effective shear depth, dv, must be defined in order to determine bo and the punching (or two-way) shear resistance. Actually, an average effective shear depth should be used since the two-way shear area includes both the "X-X" and "Y-Y" sides of the footing. In other words, dex is not equal to dey, therefore dvx will not be equal to dvy. This is illustrated as follows assuming a 3'-6" footing with #9 reinforcing bars at 6" on center in both directions in the bottom of the footing:
S5.13.3.6.3
![]()
![]()
![]()
![]()
![]()
![]() (per foot width)
(per foot width)
Effective depth for each axis:
![]()
![]()
![]()
![]()
![]()
Effective shear depth for each axis:
![]()
![]()
![]()
![]()
![]()
S5.8.2.9
![]()
![]()
S5.8.2.9
![]()
Average effective shear depth:
![]()
![]()
With the average effective shear depth determined, the critical perimeter can be calculated as follows:
![]()
![]()
![]()
![]()
The factored shear resistance to punching shear is the smaller of the following two computed values:
S5.13.3.6.3
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Define Vn_punch as follows:
![]()
![]()
![]()
![]()
With the factored shear resistance determined, the applied factored punching shear load will be computed. This value is obtained by summing the loads in the piles that are outside of the critical perimeter. As can be seen in Figure 8-12, this includes Piles 1 through 5, 6, 10,11, 15, and 16 through 20. These piles are entirely outside of the critical perimeter. If part of a pile is inside the critical perimeter, then only the portion of the pile load outside the critical perimeter is used for the punching shear check.
S5.13.3.6.1
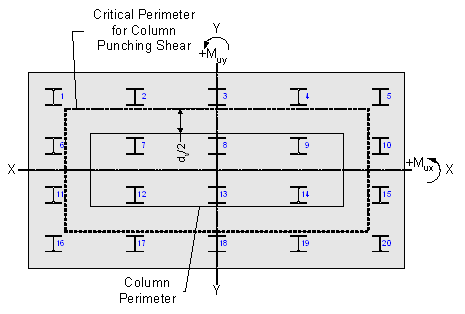
Figure 8-12 Critical Perimeter for Column Punching Shear
The following properties of the pile group are needed to determine the pile loads (reference Figures 8-11 and 8-12):
![]()
![]()
![]()
![]()
![]()
The following illustrates the pile load in Pile 1:
![]()
![]()
Similar calculations for the other piles outside of the critical perimeter yield the following:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The total applied factored shear used for the punching shear check is:
![]()
![]()
![]() OK
OK
 |
Alternate Punching Shear Load Calculation An alternate method for carrying out the column punching shear check is to simply use the applied factored axial load to obtain equal pile loads in all of the piles. This is only valid for the case where the piles outside of the critical perimeter are symmetric about both axes. The applied factored shear on the critical section is obtained as above (i.e., the sum of the piles located outside of the critical perimeter). This approach yields the same value for Vu_punch as wasderived above. This is illustrated as follows: |
![]()
![]()
![]()
It has just been shown that the factored axial load alone is sufficient for the punching shear check at the column. However, consideration of the factored axial load along with the corresponding applied factored moments is necessary for other footing design checks such as punching shear at the maximum loaded pile, one-way shear, and flexure. This applies to the abutment footing in Design Step 7 as well. However, what is unique to the pier footing is that significant moments act about both axes. What follows is a demonstration, using the pile forces previously computed, of an estimation of the applied factored load on a per-foot basis acting on each footing face. The following estimations are based on the outer row of piles in each direction, respectively. Once these estimates are obtained, the appropriate footing design checks are the same as those for the abutment footing.
![]()
![]()
Estimation of applied factored load per foot in the "X" direction:
![]()
![]()
Estimation of applied factored load per foot in the "Y" direction:
![]()
![]()
Design Step 8.12 - Final Pier Schematic
Figure 8-13 shows the final pier dimensions along with the required reinforcement in the pier cap and column.
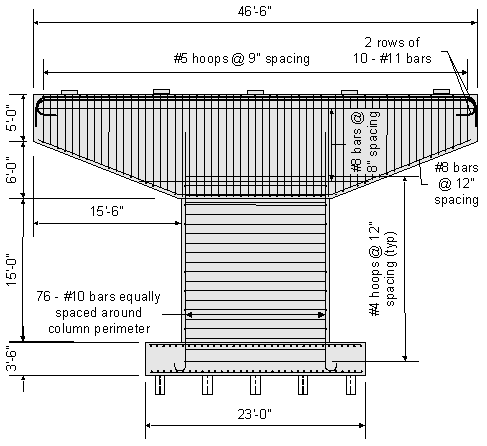
Figure 8-13 Final Pier Design
| << previous | Contents | next >> |

