U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-09-028 Date: May 2009 |
Publication Number: FHWA-HRT-09-028 Date: May 2009 |
Two commercial CFD programs were configured to model the forces on the bridge decks in simulations: STAR-CD® and Fluent®. Building the CFD model involved selecting the mesh resolution, simulation algorithm, boundary conditions including the air-water interface properties, and turbulence model. Additionally, the model simulations investigated the effect of Fr and inundation ratio on the three bridge decks in the same manner as the experimental tests.
In addition to testing the ability of the models to replicate the experimental model results, the CFD simulation had a secondary objective to determine the robustness and efficiency of the models. Due in part to scheduling constraints, the CFD model was only calibrated using the six-girder bridge deck experimental results. The same flow configurations were applied to the models of the three-girder and streamlined bridge decks. By comparing these "blind" simulation results with the experimental results, an effective test of the CFD models' general applicability was created. The CFD simulations were also conducted with attention to the efficiency of computation. Even with the TRACC facility, the high computational intensity of CFD modeling demands an efficient model setup to ensure a manageable runtime.
The setup and chosen configuration of the two models are described below.
Cd-adapco's STAR-CD® was used by researchers at the University of Nebraska at Omaha to simulate the forces acting on the three bridge decks. Like many commercial CFD models, STAR-CD® computes the overall flow of the fluid and associated forces by breaking the modeling environment into a mesh of many tiny cells. Then, the enormously complex problems of continuity and energy can be solved at the individual cell level. This project's STAR-CD® approach was based primarily on the structured hexahedral mesh option for modeling.
The STAR-CD®'s solver choices include well established pressure-based solution algorithms like the Pressure-Implicit Split-Operator (PISO) and the Semi-Implicit Method for Pressure Linked Equations (SIMPLE). Although PISO is a more robust scheme with predictor/corrector steps, the alternative SIMPLE scheme can also predict accurate results for approximately half the computational cost. Therefore, the SIMPLE solver was used for the bridge deck simulations.
To set up the numerical configuration of the simulation, the bridge dimensions and the flow conditions had to be specified.
Since water flows perpendicular to a bridge and the modeled bridge decks had regular cross sections along their length, several simplifications of the CFD model were possible and were used to test for their effectiveness in matching the experimental results and reducing computational time.
Instead of modeling the whole bridge deck at the exact dimensions of the experimental setup, the CFD model could be constructed with just a small portion of the bridge deck. The simplest model would be a true 2-D model with the bridge modeled in cross section with the thickness of only a single computational cell. To assess the validity of this approach, the 2-D model's flow field was compared to the flow field of a 3-D model that replicated the experimental setup. Instead of a full 3-D model, a half model of the bridge deck with one side along a flume wall and what was once the middle of the bridge along a symmetry boundary was used. The flow field results for the 3-D model along this symmetry plane and the 2-D model are displayed in figure 14. The flow fields indicate sufficient agreement that a 2-D model could be sufficient for the computation of the forces and moments.
The single-cell 2-D model shown in figure 14 does not provide a perfect representation of the six- and three-girder bridge due to the patterns of posts supporting the railings and voids. To account for these differences, an extended 2-D model was created so that one edge of the deck was at the midpoint of a post, and the other edge was at the midpoint of one of the void spaces. This situation is indicated by the yellow stripe in figure 15. By placing symmetry boundaries on both edges, a quasi-infinite bridge deck was simulated. The railings were simulated, as in the physical experiments, on both the leading and trailing edge of the bridge deck.
Figure 14. Image. Comparison of flow fields for the 2-D and 3-D models for the STAR-CD® simulations.
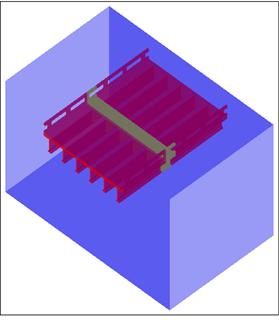
Figure 15. Image. Segment of bridge used for 3-D model.
In addition to the bridge model specification, the general simulation mesh had to be specified. Increasing the mesh resolution increased computational time, so the mesh size had to be chosen carefully. Two mesh sizes were simulated. The "coarse grid," shown in figure 16 and figure 17, had a cell size of 3.5 mm by 2.5 mm by 2.5 mm. The "partially refined" mesh increased the mesh resolution near the bridge by dividing each coarse cell into eight smaller cells by halving the cell along each dimension.
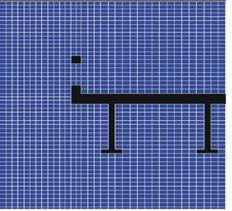
Figure 16. Diagram. Coarse meshes for STAR-CD® simulation.

Figure 17. Diagram. Partially refined meshes for STAR-CD® simulation.
The parameters of the fluid itself made up the final component of the simulation. The most important considerations were in the treatment of air-water interface and in the turbulence model selected. Advances in computational fluid mechanics have provided the basis for insight into the dynamics of multiphase flows. Since the free surface in open channel flow could be an important feature of the flow field influencing the parameters of interest defined above, the Volume of Fluid (VoF) computational technique was pursued to capture its form accurately. The VoF solution methodology was well suited for free-surface flow problems where the two fluids were separated by a well defined, sharp interface.
The VoF methodology deals with a single continuum whose properties vary according to its composition as derived from solution of transport equations for the component fluids. These component fluids are assumed to be immiscible and labeled as the base, light fluid, (in this study, air) and the heavy fluid (water). The density of each fluid component is assumed constant, and, when both components are present in a computational cell, they share the field variables (velocity and pressure) computed for the fluid mixture. The result is that water depth can vary slightly along the flow path, as it would in reality.
Since the form of the free surface was generally stable and reasonably flat in this study, especially for high inundation ratios (h* > 1), a separate set of calculations in which the top surface is at h = hu, was modeled as a flat "fixed surface" in STAR-CD®. In these single-phase (water-only) simulations, the top surface was modeled either as a slip-wall or free-stream boundary. As expected, the results of these steady-state "fixed-surface" simulations were generally consistent with the results of the "free-surface" simulations. Since the calculations with the fixed-surface models did not require a long computation time, many of the turbulence model evaluations and grid sensitivity studies were performed with the fixed-surface models in STAR‑CD®.
These turbulence models were the final major consideration in the modeling setup. Undoubtedly, the high Re flows approaching the bridge decks could be considered turbulent. Turbulent flow is highly unsteady and irregular. The available computer power was not sufficient to represent all of the eddies ranging from the smallest scale (corresponding to dissipative motions) to the largest scale (responsible for most of the momentum transport in a high speed flow). Therefore, turbulence models were used to describe turbulence based on some simplifying assumptions. STAR-CD® provides a range of turbulence modeling options, including several based on the two equation Reynolds-averaged Navier-Stokes (RANS) model and even higher order models. Ultimately, the high Re variant of the κ-ε model was selected for the detailed simulations.
ANSYS, Inc.'s ® Fluent® CFD modeling software was also used for modeling the deck forces on the bridge decks. Though Fluent® and STAR-CD® have many similar capabilities, they were used differently for this study. The following section describes the numerical configuration for Fluent®.
Though there are many mesh options, the Fluent® experiments for this study used an unstructured mesh as opposed to the structured hexahedral mesh in STAR-CD®. The unstructured mesh captures the flow around complex shapes like the bridge decks. The Tet/Hybrid mesh was chosen, which is composed primarily of tetrahedrons. Figure 18 shows a 3-D model of the six-girder bridge rendered in this mesh.

Figure 18. Model. A rendering of the 3-D six-girder bridge deck in Fluent®.
The simulations using Fluent® were performed for three different shapes of bridge deck (i.e., six- and three-girder bridge deck models with railings on both sides and streamlined bridge deck). As in the STAR-CD® simulations, 2-D and 3-D models were built and tested for the six-girder bridge deck. The 2-D model was simplified to have a solid wall instead of a railing, but the 3-D model was modeled exactly as in the experiments. The velocity maps in figure 19 and figure 20 show that there was general agreement between the 2-D and 3-D models but that the 3-D model captured more detail and was less affected by the railings.
Figure 19. Image. Velocity profile from the 2-D Fluent® model.
Figure 20. Image. Velocity profile from the 3-D Fluent® model.
The simulation mesh was also unstructured and Tet/Hybrid. All simulations were performed with a mesh that was finer in the vicinity of the bridge and coarser farther away, as shown in figure 21. All of the simulations were also performed using the VoF transient multiphase model with both air and water. Since the free surface was an important feature of open channel flow, all of the Fluent® simulations were run for the two-phase model with air and water.
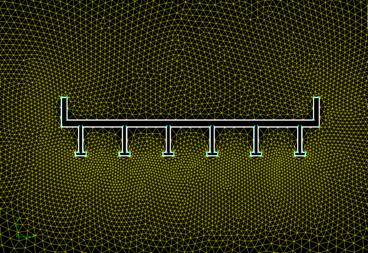
Figure 21. Diagram. Fluent® unstructured mesh in the vicinity of the bridge.
The Fluent® software also required selection of a turbulence model to complete the simulation. Two different turbulence models were used in parallel for the Fluent® simulations. The unsteady κ-ε model was selected since it was also used in the STAR-CD® simulations. Additionally, the Large Eddy Simulation (LES) model was selected since it simulates large eddy motion explicitly based on flow direction and does not perform time-averaging as the RANS models do. The LES could more faithfully resolve the turbulent flow in the model but at greater computational cost.
The first objective of the simulations was to provide estimates of the drag, lift, and moment coefficients using the same variables as in the physical experiment. That is, the simulations were conducted for approach velocities ranging from 0.25 to 0.5 m/s (Fr varied within the range of 0.16 to 0.32), and the simulations were run for various inundation ratios.
The STAR-CD® simulations modeled only the six- and three-girder bridge decks, while the Fluent® κ-ε simulations modeled all three types. The Fluent® LES simulation considered only the six-girder deck. The experimental data for six-girder bridge deck model were only available during the numerical simulations, whereas the three-girder and streamlined bridge deck experimental data were provided once the simulations were completed.