Using Falling Weight Deflectometer Data With Mechanistic-Empirical Design and Analysis, Volume III: Guidelines for Deflection Testing, Analysis, and Interpretation

CHAPTER 3. General Backcalculation Guidelines

Because the most common use of deflection data is in the backcalculation of the fundamental engineering parameters of the paving layers, this chapter has been prepared to provide general guidance on performing backcalculation. The guidelines are intended to assist the pavement engineer in conducting the backcalculation process, evaluating the results, and ensuring that those results are reasonable; however, they should be used only as general guidance because considerable engineering judgment and expertise is still required.

In addition to the guidelines on pavement backcalculation, this chapter describes the results of studies that have verified backcalculated results with instrumented pavement sections and also presents an example illustrating the interpretation of results from a backcalculation program.

Backcalculation Versus Forwardcalculation

In the backcalculation process, pavement deflections are determined using layer elastic theory, layer thickness, and assumed layer moduli (e.g., HMA layer, unbound base layer, and subgrade). An iterative approach is used to vary layer moduli until the calculated deflection basin matches the FWD-measured deflection basin. A solution is found when the difference between the measured and calculated deflection basin is minimized (discussed in the following sections).

In forwardcalculation, load and deflection data are entered into closed-form equations for estimating layer moduli. Forwardcalculation can be used to estimate layer moduli for the subgrade and bound surface layers, while intermediate layer (e.g., unbound base) moduli are estimated using modular ratios.⁽²⁴⁾

The primary difference between backcalculation and forwardcalculation is that the former uses specific equations, while the latter uses an iterative procedure in estimating layer moduli.

Backcalculation Guidelines

Over the years, researchers and practitioners have developed numerous approaches to backcalculate pavement layer and subgrade moduli, as well as numerous software programs to perform the calculations. Table 8 summarizes available software programs that can be used for backcalculation of pavement deflection data that the research team was able to identify during the conduct of this research study.

N/A = Not applicable.

Inputs Needed for Backcalculation Analysis

The following inputs are needed to perform a backcalculation analysis:

• FWD testing configuration and results (load plate diameter, sensor locations, load level, test locations, and resulting deflections).
  
  
• Pavement temperature at the time of FWD testing.
  
  
• Pavement structure (layer types (e.g., HMA, PCC, base/subbase material), layer thicknesses, Poisson’s ratio for each layer (often assumed), material density (often assumed), and subgrade).
  
  
• Modulus values, including seed or initial moduli, and modulus range.

Backcalculation Pavement Model

A number of different factors must be considered in establishing a model of the pavement section for backcalculation, as described in the following sections.

Number of Layers

Ideally, no more than three (preferable) or four layers with unknown moduli should be used in the backcalculation process. If the backcalculation results produce unrealistic weak base moduli, it may be advantageous to eliminate the base layer and evaluate the pavement structure as a two-layer system. In this case, the lower base moduli may indicate contamination from the underlying subgrade, resulting in weaker base moduli owing to the presence of finer material.⁽²⁵⁾ If unrealistic results persist, then the analysis should consider the presence of a stiff layer.

When a pavement structure consists of a stiff layer between two weak layers, the backcalculation process may produce unrealistic moduli.⁽²⁵⁾ If this is the case, other means (e.g., laboratory testing) may be required for determining layer moduli.

Thickness of Layers

The following subsections provide guidelines for setting the layer thickness for each pavement layer.

HMA

It can be difficult to obtain reasonably backcalculated moduli for bituminous surface layers less than 75 mm (3 inches) thick. If the total thickness of the bituminous layer is less than 75 mm (3 inches), the modulus of the bituminous layer should be fixed (see table 9 for guidance) to allow backcalculation of the base and subgrade moduli.

Theoretically, backcalculation of each individual bituminous layer is possible, but this is generally not advised because of the complexity of evaluating more than three or four pavement layers. Ideally, all bituminous layers (seal coats, chip seals, and HMA) should be combined into a single layer unless there is evidence of an HMA layer exhibiting a unique distress.⁽²⁷⁾ In general, the presence of stripping or debonding of HMA layers reduces the backcalculated HMA moduli. In these cases, coring may be required to confirm the presence of stripping or debonding.

PCC

There are no thickness limitations associated with the backcalculation of modulus values for concrete pavements.

Unstabilized Base/Subbase Course

The presence of a thin base course beneath a thick HMA or PCC surface layer often results in low base moduli. This can occur because of the insignificant effects of a thin base beneath a very stiff thick layer, or it may be that the base modulus is low due to the stress sensitivity of granular materials.⁽²⁵⁾ In this case, it is advisable to combine the base with the subgrade and conduct the backcalculation as a two-layer system. If consideration of the base layer is desired, including a stiff layer in the backcalculation process may improve the base/subbase layers modulus estimate.

Subgrade

If an unusually high subgrade modulus is determined from the backcalculation results, the site should be investigated for the possible presence of a shallow bedrock/stiff layer or a high water table.

Initial and Moduli Ranges

The following subsections provide guidelines for the typical range of layer moduli that should be considered in establishing a pavement section model for backcalculation.

HMA

Generally, new HMA is observed to have backcalculated moduli ranging from 2,000 to 4,000 MPa (300,000 to 600,000 lbf/inch²), while a fatigue-cracked HMA is often observed to have backcalculated moduli between 700 and 1,400 MPa (100,000 to 200,000 lbf/inch²) at about 25 °C (77 °F). In some cases, areas of severe alligator cracking can result in backcalculated HMA layer moduli that significantly exceed the expected moduli values. If the HMA layer is known to have severe alligator cracking and results in high backcalculated layer moduli, it is recommended that either the HMA layer moduli be fixed at 700 to 1,400 MPa (100,000 to 200,000 lbf/inch²) or the testing location not be used in the backcalculation analysis. However, the presence of severe alligator cracking represents an area of structural deficiency and may require repair before overlay or at least should be taken into account during the overlay thickness design process.

If an HMA modulus range is required, an initial estimate of the HMA modulus should be made and then the range can be selected as 0.25 to five times that value.⁽²⁷⁾ For example, if the initial HMA modulus estimate is 2,800 MPa (400,000 lbf/inch²), then a range of 700 to 14,000 MPa (100,000 to 2 million lbf/inch²) is selected.

PCC

The modulus of an uncracked concrete pavement typically ranges from about 10,000 to 70,000 MPa (1.5 million to 10 million lbf/inch²).⁽²⁸⁾ An initial modulus ranging from 28,000 to 40,000 MPa (4 million to 6 million lbf/inch²) is typical.

Unstabilized Bases and Subbases

Initial modulus and moduli ranges are listed in Table 10 for a variety of unstabilized base and subbase materials.

Note: Data in this table were taken from references 27-29.

Stabilized Bases and Subbases

Initial modulus and moduli ranges are presented in table 11 for a variety of stabilized base and subbase materials.

Note: Data in this table were taken from references 28 and 29.

Subgrade

Table 12 includes suggested values for subgrade moduli by soil type and climate condition.

Poisson’s Ratio

Table 13 provides recommendations for Poisson’s ratio for various paving and subgrade materials.

Depth to Bedrock/Stiff Layer or Water Table

The presence of shallow bedrock, a stiff clay layer, or high groundwater table can have a significant effect on backcalculated layer moduli. Assuming the subgrade layer to be a semi-infinite halfspace, while in reality the subgrade layer is only a few meters (feet) thick, causes the backcalculated moduli for the upper pavement layers to be incorrect. Generally, when the stiff layer is deeper than about 12 m (39 ft), its presence has little or no influence on the backcalculated moduli. The depth to the stiff layer can be evaluated by using a relationship between the deflection, δ_Z, and 1/r, where r is the corresponding offset of the measured surface deflection (see figure 20).⁽³²⁾

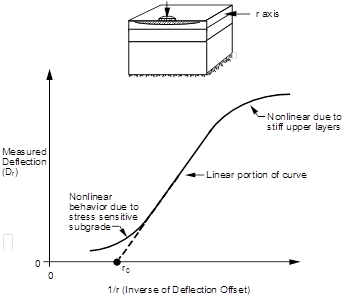
©Washington State Department of Transportation

Figure 20. Graph. Inverse of deflection offset versus measured deflection.⁽³¹⁾

The determination of the depth to the stiff layer using the offset of inverse deflection uses the following regression equations (see figure 21 through figure 24) for various HMA layer thicknesses:⁽³²⁾

Figure 21. Equation. Determination of depth to stiff layer, HMA less than 50 mm (2 inches) thick (R² = 0.98).

Figure 22. Equation. Determination of depth to stiff layer, HMA 50 to 100 mm
(2 to 4 inches) thick (R² = 0.98).

Figure 23. Equation. Determination of depth to stiff layer, HMA 100 to 150 mm
(4 to 6 inches) thick (R² = 0.94).

Figure 24. Equation. Determination of depth to the stiff layer, HMA greater than 150 mm (6 inches) thick (R² = 0.97).

Where:

B = Depth to rigid layer, measured from pavement surface (ft).
r₀ = 1/r intercept (extrapolate steepest section of D_r versus 1/r plot) in units of 1/ft.
BCI = D₂₄ - D₃₆ BCI (i.e., MLI) (mil).
BDI = D₁₂ - D₂₄ BDI (i.e., LLI) (mil).
SCI = D₀ - D₁₂ SCI (i.e., BLI) (mil).

Example of Calculating Depth to Stiff Layer⁽³¹⁾

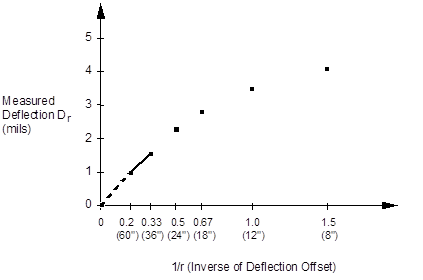
Typical deflection data for an HMA pavement section with an asphalt layer thickness of 194 mm (7.65 inches) are shown in table 14. In addition, soil borings indicate a stiff layer may be present at 5.0 m (198 inches). The corresponding values of 1/r (expressed in terms of 1/ft) are shown in table 15 for each sensor offset.

N/A = Not applicable.

With this information, the equation in figure 24, repeated here as figure 25, (for HMA thickness > 150 mm (6 inches)) is used to calculate B.

Figure 25. Equation. Determination of depth to the stiff layer, HMA greater than 150 mm (6 inches) thick (R² = 0.97).

Where:

r₀ = 1/r intercept (refer to figure 26) ≅ 0 (steepest part of deflection basin for deflections at 36 and 60 inches).

©Washington State Department of Transportation
1 mil = 0.0254 mm.
1 inch = 25.4 mm.

Figure 26. Graph. Measured deflection versus 1/r.⁽³¹⁾

Therefore, the depth to the stiff layer in this case is calculated as shown in figure 27.

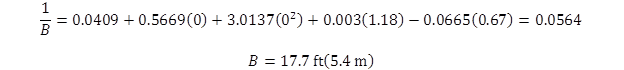
Figure 27. Equation. Sample computation of depth to the stiff layer with HMA greater than 150 mm (6 inches) thick (R² = 0.97).

Recalling that the soil boring indicated the potential of a stiff layer at 5.0 m (16.5 ft), the estimate for the depth to the stiff layer using the inverse of deflection offset agrees reasonably well. An alternative way to determine the depth to the stiff layer is to use the free vibration response from FWD deflection sensor measurements and one-dimensional wave propagation theory.⁽³³⁾ Chatti, Ji, and Harichandran modified Roesset’s equations to account for different conditions, as shown in figure 28.⁽³⁴⁾

Figure 28. Equation. Determination of depth to the stiff layer using modified Roesset’s equations.

Where:

V_s = Shear-wave velocity of subgrade = [(E_sg/(2(1 − u²))/ρ]^0.5.
E_sg = Modulus of the subgrade.
ρ = Unit weight of the subgrade.
u = Poisson’s ratio of subgrade.
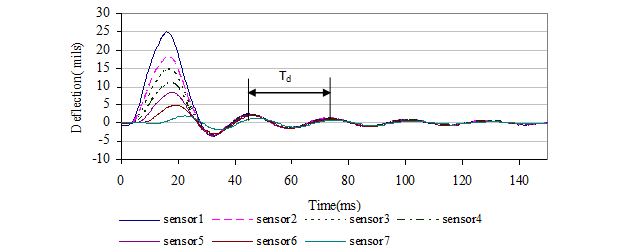
T_d = Natural period of free vibration (see figure 29).

©Chatti, K., Ji, Y., Harichandran, R.S., and Hyung, S.L.
1 mil = 0.0254 mm.

Figure 29. Graph. Illustration of natural period, T_d, from sensor deflection time histories.⁽³⁴⁾

In the backcalculation process, the stiffness of a stiff layer is often fixed at modulus values ranging from 700 to 6,900 MPa (100,000 to 1 million lbf/inch²). When a stiff layer is included, the subgrade must have a specified thickness, and the bedrock/stiff layer is assumed to have an indefinite depth. If a stiff layer is believed to exist, but exact depth data are not available, the depth in the backcalculation process should be varied (e.g., depths of 6, 9, or 15 m (20, 30, or 50 ft)) to determine whether reasonable results can be obtained. Ideally, the depth to the stiff layer should be verified by subsurface borings.

If the layer is due to the presence of a water table (or saturated soil), then a modulus value of about 345 MPa (50,000 lbf/inch²) should be used. If rock or stiff soils (e.g., glacial till) are present, then a modulus value of about 6,900 MPa (1 million lbf/inch²) may be more appropriate.

PCC Pavement Interface Conditions

The ability to account for the interface condition between a PCC slab and the underlying base/subbase layer can have a significant effect on the backcalculated results.⁽³⁵⁾ This was demonstrated on an evaluation of two LTPP Program General Pavement Studies rigid pavement sections: section 105004, consisting of a 225-mm (8.8-inch) continuously reinforced concrete pavement (CRCP) over a 100-mm (4-inch) cement-aggregate mixture, and section 204052, consisting of a 225-mm (8.8-inch) jointed plain concrete pavement (JPCP) over a 100-mm (4-inch) lean concrete base. Backcalculation scenarios include the following:

• No base: Base layer was excluded from the analysis.
• No bond: Base layer is in full slip with the PCC layer.
• Full bond: Base layer is in full friction with the PCC layer.

The results of the analysis, shown in table 16, indicate that the PCC layer moduli for the no base scenario are unreasonably high for both LTPP Program sections. The full bond assumption produces more reasonable results for section 204052, whereas the no bond scenario provides more reasonable results for section 105004.

E_PCC = PCC layer moduli.
E_Base = Base layer moduli.

Stabilized Base Under PCC Pavements

It is difficult to precisely determine the layer modulus of a stabilized base beneath a concrete slab from surface deflection data. Given that the bending stiffness of multiple pavement layers (plates) can be represented by an equivalent plate with an effective thickness (h_e) and modulus (E_e), it is not possible to resolve the backcalculated effective modulus into component moduli without having additional information on the interface bonding condition and the relative stiffness of the slab and stabilized base (also known as the modular ratio). However, these can be estimated and used iteratively to obtain reasonable estimates of the slab and base modulus values. The two equations in figure 30 can be used to determine the slab modulus value for the unbonded and bonded conditions; the stiffness of the stabilized base, E₂, can be found by multiplying the stiffness of the slab by the modular ratio, β.⁽³⁵⁾

Figure 30. Equation. Determination of slab modulus values for (a) unbonded and (b) bonded conditions.

Where:

E₁ = Modulus of upper plate, i.e., the PCC layer (MPa (lbf/inch²)).
E₂ = Modulus of lower plate, i.e., the base layer (MPa (lbf/inch²)).
h₁ = Thickness of upper plate, i.e., the PCC slab (mm (inches)).
h₂ = Thickness of lower plate, i.e., the base layer (mm (inches)).
β = Modular ratio (see table 17 for selection).

Modeling and Response Issues

The pavement responses to loading can be modeled and interpreted in different ways as part of the backcalculation process. Some of these issues, and how they are often addressed, are described in the following subsections.

Static Versus Dynamic Response

The difference between static response and dynamic response can be defined in terms of the internal forces involved. In a static analysis, only elastic forces are considered, and it is assumed that the peak deflection at each sensor occurs at the same time as the peak load. In actually, viscous and inertial forces are at work in the pavement system, and there is a significant time lag between the peak load and the peak deflection for each sensor. A dynamic analysis tries to capture these time lag effects.

Many engineers argue that backcalculation is an exercise that determines pavement parameters, and not properties, to use within a given mechanistic framework. Therefore, it is acceptable to use static analysis and to backcalculate parameters that are compatible with the current mechanistic-empirical design framework grounded in static and not dynamic analysis. However, dynamic analysis advocates maintain that it takes advantage of more information provided by the test, which allows backcalculating more parameters such as layer thicknesses or the modulus versus frequency curve of the HMA layer. (See references 34 and 36-38.) Also, in certain cases, such as the existence of a stiff layer or water table at shallow depth, the effect of dynamics of pavement response may become more important.

Linear Versus Nonlinear Behavior

When pavement structures are thin enough or the applied loads and corresponding stresses are high enough, fine-grained subgrade materials often exhibit stress-softening, nonlinear behavior (i.e., the subgrade material response increases at a higher rate than the load or stress increases). This means that the subgrade modulus changes with depth and with radial distance from the load. If the modeling approach assumes linear behavior, then only a single modulus value can be assigned to the subgrade, typically an averaged value that matches the measured deflections. For fine-grained materials, the backcalculated subgrade modulus is commonly higher than the laboratory-based measurement by a factor of two to three.

On the other hand, granular (cohesionless) materials used in bases and subbases are stress dependent in a different way, in that their modulus increases with increasing confinement. Similar to the subgrade modulus, this leads to a base/subbase modulus that varies with depth and radial distance from the load, and any linear backcalculation exercise can only lead to an averaged modulus value. The combination of the above phenomena often leads to a base modulus lower than the subgrade modulus even through the base material is of higher quality than the subgrade. Although one way of addressing this problem is to introduce an artificial layer, a more direct way of addressing the problem is to treat the subgrade as a nonlinear elastic material with stress-dependent modulus as shown in figure 31.⁽³⁹⁾

Figure 31. Equation. Stress-dependent modulus determination.

Where:

E = Modulus value (MPa (lbf/inch²)).
C = Positive constant.
n = Negative constant.
p = Reference stress (atmospheric pressure of 0.1 MPa (14.5 lbf/inch²)).

Ullidtz argues that the effect of the positive non-linearity in granular base/subbase layers is less important to the backcalculation results.⁽³⁹⁾

Although finite element modeling (FEM) can be used to evaluate the variation of modulus with depth and radial distance, models based on layered elastic theory can also handle nonlinear behavior (e.g., NELAPAVE and KENPAVE). For example, Ullidtz combines the method of equivalent thickness with a stress-dependent subgrade modulus (see figure 31 equation) to handle material nonlinearity and reports that this approach is superior to FEM.⁽³⁹⁾

A number of backcalculation programs, such as BOUSDEF, EVERCALC©, FPEDD1, MODTAG©, and RPEDD1, include a nonlinear analysis component. Others, such as ELMOD®/ELCON, EMOD, ISSEM4, and PADAL, incorporate a nonlinear analysis for the subgrade only.

Temperature and Moisture Effects

Temperature and moisture conditions in the pavement vary over time, both daily and seasonally. A pavement is generally stiffer (stronger) during the winter months because of the frozen state of the underlying materials and is typically at its weakest during the spring thaw period when the foundation materials are saturated.

Several State transportation departments have conducted FWD testing on multiple locations over consecutive seasons to determine the seasonal variation in the unbound layer moduli.⁽⁴⁰⁾ Based on the results of the studies, these agencies have developed a range of seasonal factors (see table 18) for adjusting layer moduli for use in a HMA overlay design procedure. In addition, the Enhanced Integrated Climatic Model (EICM), which is incorporated in the MEPDG, provides an analytical tool for predicting temperature, resilient modulus adjustment factors, pore water pressure, water content, frost and thaw depths, frost heave, and drainage performance for a given pavement.⁽¹⁾

—Indicates no data.

Temperature and moisture effects are also critical for PCC pavements because slab curling (caused by temperature gradients) and slab warping (caused by moisture gradients) significantly influence the deflection response of PCC pavements. For example, Khazanovich, Tayabji, and Darter showed backcalculated k-values at one location to be up to three times as high because of temperature gradients.⁽³⁵⁾ In addition, temperature effects are more critical on backcalculated k-values for thinner slabs compared with thicker slabs.⁽⁴²⁾ However, it is primarily large temperature fluctuations (temperatures outside of 7 to 32 °C (45 to 90 °F)) that influence the backcalculated slab modulus and k-values.⁽⁴³⁾

None of the existing analysis methods directly accounts for the effects of temperature or moisture in the backcalculation process. Therefore, it is recommended that FWD testing be performed when there is no significant temperature gradient present (e.g., when the ambient air temperature is below 27 °C (80 °F)) to avoid the effects of slab curling on the backcalculated results. Note, however, that avoiding the temperature gradient will not address any built-in curling that may be present in the pavement. Crovetti presents a way of differentiating slab curling from poor foundation support using an incremental analysis.⁽⁴⁴⁾

Slab Size Effects

PCC pavement backcalculation procedures based on Westergaard’s solutions assume an infinite plate, but in actuality, pavements have a finite length and width. The following approach can be used to correct for slab size effects on a bare PCC pavement during the backcalculation process:⁽⁴⁵⁾

1. Compute AREA (units of inches) for the seven-sensor configuration (sensors spaced at
   (0, 203, 305, 457, 610, 914, and 1,524 mm (0, 8, 12, 18, 24, 36, and 60 inches)), as described in chapter 2.
2. Compute the estimated radius of relative stiffness (ℓ_est) (units of mm (inches)) for an infinite slab using the equation in figure 32 for the seven-sensor configuration:

Figure 32. Equation. Estimate of radius of relative stiffness for an infinite slab.

3. Estimate the modulus of subgrade reaction (k-value) for an infinite slab using figure 33.

Figure 33. Equation. Estimate of modulus of subgrade reaction for an infinite slab.

Where:

k_est = Modulus of subgrade reaction (MPa/mm (lbf/inch²/inch)).
P = Applied load (N (lbf)).
d₀* = Nondimensional deflection coefficient of deflection at center of load plate =
d₀ = Measured deflection at radial distance r from the load (mm (inches)).
ℓ_est = Estimated radius of relative stiffness (mm (inches)).

4. Calculate finite slab size adjustment factors for the deflection directly under the load plate (AF_d0) and radius of relative stiffness (AFℓ_est) using figure 34 and figure 35 equations.

Figure 34. Equation. Adjustment factor for radius of relative stiffness.

Figure 35. Equation. Adjustment factor for deflection directly under load plate.

Where:

L = (Ll × Lw) × 0.5 (if the slab length, Ll, is less than or equal to twice the slab width, Lw).
L = 1.414 × Ll (if the slab length, Ll, is greater than twice the slab width, Lw).

5. Calculate the adjusted k-value that accounts for slab size effects as shown in figure 36):

Figure 36. Equation. Adjusted k-value calculation for slab size.

Although the slab size correction procedure is relatively simple and straightforward, it is not always used because of the difficulty in defining the effective length and width of the slab, which are a function of the LTE at the adjacent joints.⁽³⁵⁾

Measures of Convergence

In the backcalculation process, the goodness of fit between the calculated deflection basin and the measured deflection basin is referred to as the measure of convergence. The root mean square (RMS) error is one of the more common measures of convergence and can be used to provide a measure of the magnitude of the difference between the calculated and measured deflection basin; it is computed as shown in figure 37.

Figure 37. Equation. Determination of RMS error.

Where:

n_d = Number of deflection sensors used in the backcalculation process.
d_ci = Calculated pavement surface deflection at sensor i.
d_mi = Measured pavement surface deflection at sensor i.

Figure 38 illustrates an example calculation for RMS using the summary of measured and computed deflections provided in table 19.⁽²⁷⁾

Figure 38. Equation. Example RMS calculation.

Based on analysis of LTPP Program data, Von Quintus and Killingsworth suggested that an error term of 2 percent or less was considered reasonable.^(46,47) The EVERCALC© and MODTAG© user manuals indicate a RMS error of less than 1 percent will result in credible estimates of the layer moduli, whereas layer moduli results with a RMS error greater than 3 percent should be considered questionable.^(31,48) Based on these guidelines, the resulting RMS error from the example described in figure 38 and table 19 is considered higher than normally accepted, and therefore resulting layer moduli should be scrutinized.

Modulus Convergence

In addition to the deflection convergence measure, some backcalculation programs also include convergence criteria based on changes in the estimated moduli. If the change in layer moduli between subsequent iterations is less than a user-specified limit, the backcalculation process will terminate. Figure 39 shows the general form of the modulus convergence equation.⁽²⁷⁾

Figure 39. Equation. Determination of modulus convergence.

Where:

MT = Difference in layer moduli from one iteration (k) to the next (k + 1).
E_i^(k) = Specific layer modulus for the i-th layer at the kth iteration.
E_i^(k+1) = Specific layer modulus for the i-th layer at the (k + 1)-th iteration.

In general, a modulus convergence of 1 percent is considered acceptable. Large convergence errors suggest that there is a fundamental problem with a specific backcalculation effort. The problem could be within the deflection data (e.g., check that the sensor location in the backcalculation program corresponds to the FWD sensor locations and the precision of the deflection measurement), layer types and thicknesses, or lack of material homogeneity (e.g., cracked and uncracked conditions). Although low convergence errors are desirable, higher convergence errors do not always imply that the backcalculated layer moduli are unreasonable. In this instance, having a good understanding of material properties will greatly assist in balancing the convergence error and reasonable layer moduli.

Identifying Outliers

One of the more challenging aspects of backcalculation is deciding whether the determined layer modulus values are reasonable. Although evaluating the value of the calculated error is helpful, it does not necessarily guarantee that the results are reasonable. Ultimately, being able to assess the reasonableness of the results is based on knowledge of material parameters and behavior and is gained with experience in the backcalculation process. However, the following items are recommended for investigation when evaluating the validity of the backcalculated modulus values:

• Confirm that the error term is within desired tolerances (e.g., RMS is less than 2 percent).
  
  
• Confirm that the backcalculation inputs correspond to the FWD sensor location.
  
  
• Confirm the thicknesses of the individual layers. Ideally, the thickness of the HMA layer should be within 13 mm (0.5 inches) of the actual thickness. The base and subbase courses are less sensitive to layer thicknesses.
  
  
• Review the FWD data to identify any potential sources for the high error.
  
  
• Review the pavement condition to determine whether any unique distresses (e.g., severe rutting or severe cracking) may have led to the high error.

If investigation of these items does not provide any insight regarding the high error term, the data should be considered an outlier and removed from the analysis.

Other Effects

Several other issues may arise during the backcalculation analysis that can affect the results, including the following:⁽⁴⁹⁾

• Major cracks in the pavement, or testing near a pavement edge or joint, can cause the deflection data to depart drastically from the assumed conditions.
  
  
• Layer thicknesses are often not known or not well defined, and subsurface layers can be overlooked.
  
  
• Layer thicknesses are not uniform, and materials in the layers are not homogeneous.
  
  
• Some pavement layers are too thin to be backcalculated in the pavement model.
  
  
• Random and systematic errors exist in deflection data.

Verification of Backcalculation Results

There are potentially two ways to verify the reasonableness of backcalculated modulus values. One way is to compare measured strains with calculated strains, and the other way is to compare backcalculated modulus values with laboratory-based values. These are described in the following subsections.

Comparison Based on Strain

A number of studies have compared strains levels induced by an FWD with those of an instrumented HMA pavement. In one study, Winters conducted an evaluation at a test track pavement consisting of a 140-mm (5.5-inch) HMA layer over a 330-mm (13-inch) granular base.⁽⁵⁰⁾ HMA cores were instrumented with horizontal and transverse strain gauges and inserted into the existing HMA surface material. An FWD load was applied to induce the strain response (measured by the strain gauges mounted on the cores). The EVERCALC© backcalculation program was then used to determine layer moduli from the measured deflection basins and the corresponding strains.⁽²⁷⁾ The relative agreement between the measured and calculated strains was fairly good, as indicated in figure 40 and figure 41.

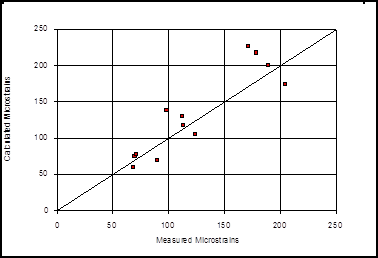
©J.P. Mahoney.

Figure 40. Graph. Measured versus calculated strain for axial core bottom longitudinal gauges.⁽⁵⁰⁾

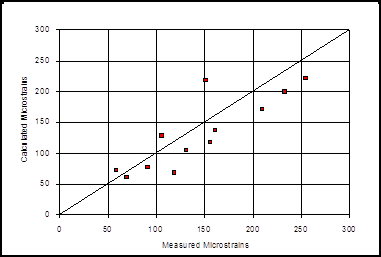
©J.P. Mahoney.

Figure 41. Graph. Measured versus calculated strain for axial core bottom transverse gauges.⁽⁵⁰⁾

In a study conducted by Lenngren, backcalculated layer moduli, determined using a modified version of EVERCALC©, were used to estimate tensile strain at the bottom of the HMA for two in-place pavement sections.⁽⁵¹⁾ In situ tensile strains were measured using strain gauges attached to HMA cores and tested using the FWD. The pavement sections of that study consisted of either 80 or 150 mm (3.1 or 5.9 inches) of HMA over a 550- to 620-mm (22- to 24-inch) gravel and sand base and granular subgrade. The results of the study are shown in figure 42 and figure 43, again showing good agreement between measured and calculated tensile strains.

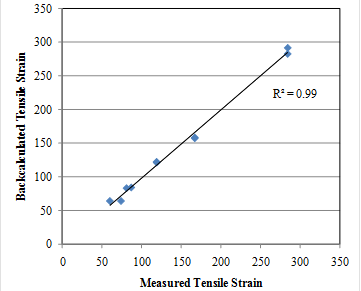
©C.A. Lenngren.

Figure 42. Graph. Backcalculated versus measured tensile strains (80-mm (3.1-inch) HMA).⁽⁵¹⁾

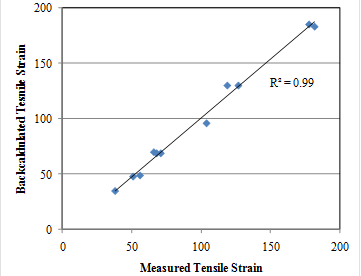
©C.A. Lenngren.

Figure 43. Graph. Backcalculated versus measured tensile strains (150-mm (5.9-inch) HMA).⁽⁵¹⁾

In a study conducted by the Minnesota Department of Transportation, in situ strain gauges were monitored during FWD testing and compared with backcalculated strain values from each of several backcalculation programs evaluated (EVERCALC©, WESDEF, and MODCOMP©).⁽⁵²⁾ The Mn/ROAD analysis concluded that the agreement between the expected and backcalculated strain (figure 44 and figure 45) was good for all programs evaluated, especially for the horizontal strain in the asphalt concrete (AC) layer.

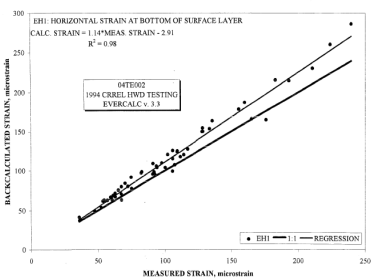
©D. Van Deusen.

Figure 44. Graph. Comparison of backcalculated (EVERCALC©) and measured AC strain.⁽⁵²⁾

©D. Van Deusen.

Figure 45. Graph. Comparison of backcalculated (WESDEF) and measured AC strain.⁽⁵²⁾

Timm and Priest also conducted a study that measured the strain response due to FWD loading and compared it with the layer moduli estimates from the WESLEA pavement analysis program.⁽⁵³⁾ Conclusions from this analysis determined that the field-measured strain was very similar to the predicted strains using the backcalculated layer moduli (see figure 46).

©D.H. Timm.

Figure 46. Graph. HMA strain comparison.⁽⁵³⁾

Appea, Flintsch, and Al-Qadi compared pavement responses (from in situ pressure cells and strain gauges) from the Virginia Smart Road with backcalculated layer moduli from measured FWD deflections.⁽⁵⁴⁾ Conclusions from this study indicate that, in general, the calculated stresses were comparable to the measured stresses.⁽⁵⁴⁾

Laboratory Versus Backcalculated Moduli

There have been a number of attempts to relate laboratory-based modulus values to those determined from backcalculation, but such comparisons can be problematic for a number of reasons, including the following:⁽²⁷⁾

• It is difficult to remold laboratory compacted samples (base, subbase, and subgrade) to the exact field structure, density, and/or moisture conditions.
• The induced loading (stress) from FWD testing is different than that of laboratory tests.
• Sampling for laboratory testing may not fully represent field conditions (e.g., sampling a subbase or improved fill material when intending to sample the subgrade soils).
• In situ pavement materials are not homogeneous.

In a study of LTPP Program rigid pavement sections, the backcalculated slab modulus values did not correlate well with the static chord modulus measured in the laboratory under ASTM C469, “Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression.”^(35,55) The backcalculated modulus values were substantially higher than the measured static values, part of which was attributed to curling/warping of the slab and also differences in the loading condition.

A number of studies have been conducted to compare backcalculated and laboratory-determined HMA layer moduli. In a study conducted by Zhou, it was determined that backcalculated HMA layer moduli were generally 20 to 30 percent lower than laboratory-measured moduli (tested at the same temperature).⁽⁵⁶⁾ More recently, Kim, Ji, and Siddiki noted that on average, the modulus determined from FWD testing was approximately two times higher than the laboratory-determined modulus.⁽⁵⁷⁾ A study by Dawson et al. found a reasonable relationship (see table 20) between laboratory and backcalculated modulus values for the following Unified Soil Classification System (USCS) soil types: gravelly sand (SP1, and SP2), poorly graded sand - silty sand (SP-SM), and clayey sand - silty sand (SC-SM), while noting that differences existed with finer grained soils types.⁽⁵⁸⁾ In a study on the effects of reflective cracking, researchers found a reasonable match between backcalculated modulus values and laboratory-based values.⁽⁵⁹⁾

SM = Silty sand.
SC = Low plasticity clay.
ML = Low plasticity silt.

Van Deusen, Lenngren, and Newcomb compared laboratory to backcalculated layer moduli for subgrade soils at the Mn/ROAD facility.⁽⁶¹⁾ This study suggested that the laboratory samples and backcalculated layer moduli compared well, within the encountered variability.⁽⁶¹⁾ Finally, a study conducted by Houston, Mamlouk, and Perera went a step farther by adding an assessment of quality related to laboratory testing costs.⁽⁶²⁾ That study concluded the following:⁽⁶²⁾

• Good agreement between laboratory testing and backcalculated results should not be expected because material “heterogeneity in any layer contributes to different measured moduli” between laboratory and field testing.
• Laboratory testing typically costs 60 to 80 times FWD testing.
• Typically, moduli determined from the backcalculation of FWD testing results are “of higher quality and more appropriate for mechanistic pavement design than lab-measured moduli.” The primary contributor to this conclusion is the disturbance during material sampling for laboratory testing.

The intent of this discussion is not to resolve the conflict between laboratory-determined and backcalculated layer moduli. Instead, the intent is to demonstrate potential issues with laboratory test results from field samples (cores of bound materials and remolded unbound materials) and to provide results of a few studies that have compared laboratory and backcalculated layer moduli. The issue of laboratory-based versus backcalculated modulus values commonly comes up in HMA overlay design with regard to whether the backcalculated layer moduli should be “corrected” to laboratory conditions. Although most HMA overlay design procedures rely on the conversion of backcalculated values to those based on laboratory conditions, an understanding of the principles and processes of both laboratory testing and backcalculation are essential for determining appropriate input values. Ultimately, the need for a correction should be based on the experience of the design engineer in concert with knowledge of the local materials and climatic conditions.

Backcalculation Example

This section provides an example of the backcalculation process using actual field data (coring, pavement condition assessment, and FWD testing results) from the Washington State Department of Transportation.⁽³¹⁾

Project Description

FWD testing was performed on a section of State Route 395 near Chewelah, WA, located in the northeast corner of the State. The pavement at the time of FWD testing (performed in mid-April) exhibited 5 to 15 percent of low- to medium-severity alligator cracking and 30 percent medium- to high-severity longitudinal cracking.

The subgrade was very deep and moderately well drained and classified as a silty loam (i.e., ML). From February to April, a perched water table was present and located at a depth of 600 to 900 mm (24 to 35 inches) beneath the surface. The base material consisted of a silty sandy gravel or sandy gravel and varied in thickness from 300 to 450 mm (12 to 18 inches). The wearing surface was composed of multiple layers of HMA and chip seal overlays with a total thickness ranging from 100 to 300 mm (3.9 to 11.8 inches). Table 21 presents a summary of the pavement cross section information based on cores taken at various points throughout the project.

Because of the presence of the perched water table, there was the potential for a stiff layer to be encountered as part of the backcalculation process. Therefore, the following three backcalculation approaches were considered:

• Assume that no stiff layer exists.
• Assume a stiff layer with a modulus of 345 MPa (50,000 lbf/inch²), which indicates a moist or saturated layer.
• Assume a stiff layer with a modulus of 6,900 MPa (1 million lbf/inch²), which indicates a rock layer or stiff deposit.

Input Values

The number of layers to be modeled for this problem ranged from three (if a stiff layer did not exist) to four (if a stiff layer existed). Table 22 summarizes the layer information and initial assumptions/ranges for modulus values. The FWD testing employed a six-sensor configuration with sensor spacings of 0, 203, 305, 610, 914, and 1219 mm (0, 8, 12, 24, 36, and 48 inches). FWD data were normalized to a standard loading of 40 kN (9,000 lbf), with the resultant normalized deflection data presented in table 23. The pavement temperature at the time of FWD testing was between 8 and 10 °C (46 and 50 °F).

^aDenotes the use of a stiff layer.
—Indicates not applicable.

Backcalculation Results

The EVERCALC© program was used in the backcalculation analysis of the FWD data collected for this project. It is briefly described in this subsection along with a presentation and discussion of the overall results.

EVERCALC©

EVERCALC© uses the Levenberg-Marquardt minimization algorithm that seeks to minimize an objective function formed as the sum of squared relative differences between the calculated and measured surface deflections.⁽⁶³⁾ EVERCALC© employs the WESLEA computer program for forward calculations; has the option for including stress sensitivity of unstabilized materials and stresses and strains at various depths; and optionally normalizes HMA modulus to a standard temperature. The program uses an iterative approach in changing the moduli to match theoretical and measured deflections and was specifically developed to backcalculate layer moduli of flexible pavements.

Discussion of Results

The backcalculation results obtained from the EVERCALC© program are shown in table 24. The E_adj columns are the backcalculated HMA modulus values adjusted to a standard temperature of 25 °C (77 °F), while the E_HMA columns are the backcalculated HMA modulus values at the actual field testing temperatures.

No Stiff Layer Scenario

In general, the adjusted HMA modulus values appear to be reasonable (within the expected moduli range for a fatigued HMA) for this aged and distressed HMA pavement. At MP location 210.50, the resulting adjusted HMA moduli was very high considering that the HMA was cracked full depth at this location. Reviewing the results for the base layer, it is noted that for the most part, the base layer moduli were higher than those determined for the subgrade, which was an expected outcome (although it may occasionally be possible for the backcalculated subgrade moduli to be equal to or slightly higher than the backcalculated base moduli). The backcalculated moduli of 35 MPa (5,000 lbf/inch²) for the base and subgrade moduli was the minimum value specified in the EVERCALC© program, which was the result at several locations for the base layer. The RMS error for more than half of the locations (54 percent) was below the recommended 2-percent threshold.

Stiff Layer at 345 MPa (50,000 lbf/inch²)

In this scenario (in which a stiff layer was assumed with a fixed modulus of 345 MPa (50,000 lbf/inch²)), the HMA modulus still appears reasonable and the base layer modulus, for the most part, increased slightly to more reasonable values. The subgrade modulus was lowered a bit from the first scenario but is still in the reasonable range for this soil type. In this scenario, 62 percent (or one more location than the first scenario) of the backcalculated moduli resulted in an RMS error below 2 percent.

Stiff Layer at 6,900 MPa (1 million lbf/inch²)

This scenario assumed a stiff layer with a fixed modulus of 6,900 MPa (1 million lbf/inch²). This analysis produces generally reasonable HMA modulus values and yields base layer moduli within the expected range for about half of the locations; it also produces slightly lower subgrade moduli but ones that are still within the range of expected values. Under this scenario, fewer than half (approximately 46 percent) of the locations had a resulting RMS error below 2 percent.

Selection of Moduli

Of the 13 locations evaluated, only 1 location, MP 209.00, consistently resulted in a very high RMS error under all three scenarios. Consequently, that point was considered an outlier and should not be considered as representative of the typical conditions. Several other locations produced RMS errors above the 2 percent criterion, but in most of those cases, one of the two stiff layer scenarios produced reasonable values. Ultimately, it is up to the engineer to decide which set of backcalculated modulus values is the most reasonable for each location, based on experience and knowledge of the in situ conditions. In general, the backcalculated moduli using a stiff layer at 345 MPa (50,000 lbf/inch²) appears to have the most locations in the range of expected values for this roadway section. Based on the information provided in this example, table 25 summarizes recommended moduli and provides a brief discussion on the reasoning behind the selection of the particular layer moduli results.

¹Scenario 1 = Stiff layer at 345 MPa (50,000 lbf/inch²)—stiff layer. Scenario 2 = Stiff layer at 6,900 MPa
(1 million lbf/inch²)—high stiff layer.
—Indicates results not recommended for use.

Summary

This chapter provides an overview of the backcalculation process and recommended guidelines for backcalculation of flexible, rigid, and composite pavements. General backcalculation recommendations are summarized as follows:

• Number of layers: Three or four, ideally no more than three layers (combine similar layers if needed).
• Layer thickness.
  • HMA: Not recommended for layers less than 75 mm (3 inches); all bituminous layers should be combined.
  • PCC: No known limitations.
  • Unstabilized base/subbase: If backcalculation results in unrealistic layer moduli and the base is relatively thin, consider combining base thickness into the subgrade to potentially reduce the error.
  • Subgrade: If backcalculation results in high error, determine/evaluate the presence of a stiff layer (bedrock, saturated layer, or water table).
• Initial moduli ranges.
  • Sound HMA: 2,000-4,000 MPa (300,000-600,000 lbf/inch²).
  • Fatigued HMA: 700-1,400 MPa (100,000-200,000 lbf/inch²).
  • PCC: 20,000-27,500 MPa (3 million-4 million lbf/inch²).
  • Unstabilized base/subbase: 100-345 MPa (15,000-50,000 lbf/inch²); see also table 10.
  • Stabilized base: 2,000-4,000 MPa (300,000-600,000 lbf/inch²); see also table 11.
  • Subgrade: 41-345 MPa (6,000-50,000 lbf/inch²); see also table 12.
• Poisson’s ratio.
  • HMA: 0.35.
  • PCC: 0.15-0.20.
  • Unstabilized base/subbase: 0.35.
  • Stabilized base: 0.25-0.35.
  • Subgrade: 0.35-0.45.

In addition, table 26 provides a summary of guidance for dealing with a number of specific issues in the backcalculation of flexible, rigid, and composite pavement systems.