Using Falling Weight Deflectometer Data With Mechanistic-Empirical Design and Analysis, Volume III: Guidelines for Deflection Testing, Analysis, and Interpretation

CHAPTER 4. Use of Deflection Data in the MEPDG

Introduction to Mechanistic-Empirical Pavement Design

As previously described, the mechanistic-empirical pavement design process attempts to correlate the development of critical responses in a pavement structure (such as stress, strain, or deflection) to pavement performance. There are a number of benefits to the use of a mechanistic-based pavement design procedure, including the following:

• Accommodation of changing loads and volumes.
• Quantification and better utilization of locally available materials.
• Material parameters that relate better to actual pavement behavior and performance.
• Ability to accommodate new materials.
• Accommodation of environmental and aging effects on materials.
• Improved characterization of existing pavement layer parameters.
• Improved reliability of performance prediction.

Although the concept of mechanistic-empirical pavement design has been around for decades, the recent development and release of AASHTO’s MEPDG as an interim edition in 2008 has generated renewed interest as agencies contemplate the adoption of the new procedure.⁽²⁾

Mechanistic-Empirical Pavement Design Principles

There are five fundamental components that make up a mechanistic-empirical based pavement design procedure: characterization of the existing pavement structure (when applicable), traffic (loading) estimation, new material characterization, climate representation, and performance prediction. These key areas are described in the following sections.

Characterization of the Existing Pavement Structure

Characterizing the load-carrying capacity of the existing pavement structure is critical for quantifying needed rehabilitation treatments. Typically, this can be determined by identifying existing pavement distress (cracking, rutting, roughness, spalling, raveling, and delaminations), obtaining pavement cores for quantifying overall layer condition and layer thicknesses, collecting subsurface samples for subgrade strata identification and thickness determination, and performing pavement deflection testing for quantifying pavement deflection response and for computing deflection basin parameters and pavement layer moduli.

Pavement Condition Evaluation

A pavement condition evaluation is generally associated with a visual survey of the pavement surface in which pavement distresses are identified and quantified. Most highway agencies have their own standardized distress survey methods, and the FHWA’s LTPP Program also has produced a distress survey manual.⁽⁶⁴⁾

Pavement Coring

A critical input in the backcalculation process is accurate layer thickness information. Although project documents, such as as-built drawings, are often the source of layer thickness information, coring the pavement to obtain in-place thicknesses is the preferred alternative when feasible. In addition to the layer thickness, retrieving pavement cores allows the opportunity for a visual assessment of the pavement layers, such as the following:

• Condition at the bottom of the surface layer.
• Condition of underlying stabilized layers.
• Bonding condition between pavement layers.
• Relative compaction/consolidation.
• Indication of materials-related problems.

Subsurface Borings

Subsurface borings identify the type and thickness of subgrade strata and provide material samples for laboratory testing and visual soils classification. Subsurface information important to the backcalculation of deflection data also includes the depth to bedrock/stiff layer or depth of the water table, if present. Subsurface boring, typically to a depth of 3 m (10 ft), is often performed at the same locations as coring.

FWD Testing

Deflection testing can be used to assess the structural condition of existing pavements, assist in the design of structural overlays, appraise seasonal variations in pavement response, assess structural variability along a project, and characterize paving layer parameters and subgrade support conditions. For rigid pavements, deflection testing can also be used to determine load transfer across joints and cracks and to detect underlying voids.

Other Project Testing

A number of other specialized testing procedures can be performed during project evaluations and include ground-penetrating radar (GPR), seismic testing methods, and dynamic cone penetrometer (DCP) testing. One of the primary uses of GPR is in the determination of pavement layer thicknesses, which can be of tremendous value when backcalculating layer moduli. Examples of seismic test methods include seismic analysis of surface waves (SASW), impact echo (IE), and impulse response (IR), all of which can be used to determine layer moduli and thicknesses. DCP testing can be used to complement FWD results in the determination of unbound layer strengths.

Traffic Estimation

The majority of mechanistic-empirical pavement design procedures have been developed around the use of an equivalent single-axle load (ESAL) for characterizing traffic. With the implementation of the MEPDG, traffic characterization is now based on axle load spectra, which account for the number and magnitude of truck traffic loadings for FHWA class 4 vehicles and above.^(1,65)

New Material Characterization

Pavement materials are typically characterized in terms of their modulus and Poisson’s ratio. In practice, assumed values for Poisson’s ratio are acceptable for the majority of mechanistic-empirical pavement design procedures because the resulting designs are not overly sensitive to this input. Typically, layer moduli for new pavement materials are characterized through laboratory testing, based on historical knowledge, or based on engineering-based assumptions.

Climate Representation

Because many materials (e.g., HMA and fine-grained soils) are temperature and/or moisture sensitive, the majority of mechanistic-empirical based pavement design procedures incorporate processes for including seasonal temperatures and moisture effects. In a mechanistic-empirical pavement design process, climatic effects are included to adjust layer moduli in response to seasonal effects. For example, HMA modulus values decrease during warmer temperatures but increase under colder conditions. To more accurately characterize the materials over the analysis period, these variations in layer moduli must be considered.

Performance Prediction

The empirical portion of the mechanistic-empirical pavement design process includes the relationship between material parameters and the estimated number of loads to failure. This information is obtained by observing pavement performance and relating the observed failure to an initial strain (or stress) under various traffic loads.

Flexible Pavement Responses

For flexible pavements, the primary means of mathematically modeling a pavement structure is layered elastic analysis. The modulus of elasticity, Poisson’s ratio, and layer thickness (i.e., each layer is assumed to extend indefinitely in the horizontal direction, and the subgrade extends indefinitely downward) are used to define the parameters of each material layer. From these material parameters and loading conditions stress, strain, and pavement deflections can be computed.

Layered elastic analysis computer programs can be used to calculate the theoretical stresses, strains, and deflections anywhere in a pavement structure. Figure 47 illustrates the locations of the critical HMA pavement response locations.

Figure 47. Diagram. HMA pavement response locations.

These response locations are further described as the following:

• The horizontal tensile strain at the top and bottom of the AC layer is used in determination of fatigue cracking.
• Compressive vertical stress/strain within the HMA layer is used in the determination of rutting within the HMA layer.
• Rutting in the base/subbase layers is determined using the compressive vertical stress/strain within the base/subbase layers.
• Rutting failure in the subgrade can be predicted using the vertical compressive stress/strain at the top of the subgrade.

Rigid Pavement Responses

The pavement responses critical to the performance predictions of rigid pavements include (1) deflections at the slab corners that contribute to faulting and (2) tensile stresses at midslab that result in fatigue cracking. Factors affecting corner deflections and midslab stresses include thermal curling, moisture warping, thermal expansion and contraction, and traffic loadings.

Thermal curling is the result of differences in temperature between the top and the bottom of the slab and the restriction to these changes caused by the weight of the slab itself (see figure 48). Moisture warping, on the other hand, develops owing to differences in the moisture content between the top and bottom of the slab. Curling and warping in the slab influence both the midslab stresses and the corner deflections. The magnitude of the midslab stresses is also influenced by restraint forces caused by friction at the slab/base interface as the slab expands and contracts under changing temperature conditions.

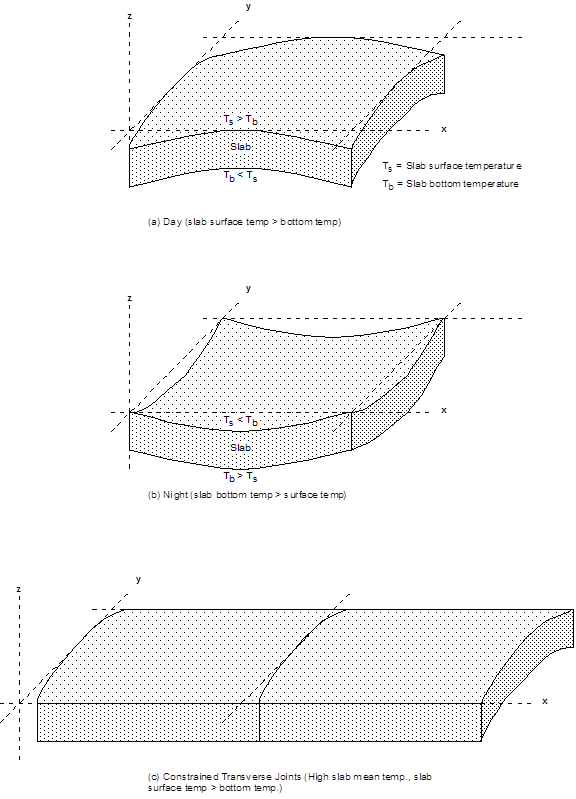
©Washington State Department of Transportation

Figure 48. Diagrams. Thermal curling stress for (a) day (b) night, and (c) constrained transverse joints.⁽²⁷⁾

The final factor affecting slab responses is the applied vehicle loads. While the critical load location for faulting predictions is at the corner of the slab, the critical load location for fatigue cracking is a function of the shape of the slab at the time of loading. The slab is susceptible to top-down cracking when there is upward curvature and the axles are spaced such that the approach and leave joints are being loaded simultaneously. Damage related to bottom-up cracking occurs when the axle is located at midslab and when the slab is flat or upward curvature is present. These critical loading conditions are depicted in figure 49.

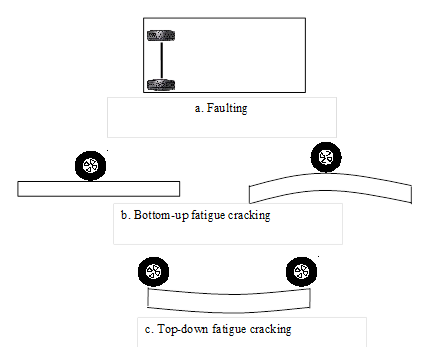
Figure 49. Diagrams. Critical loading conditions: (a) faulting, (b) bottom-up fatigue cracking, and (c) top-down fatigue cracking.

Selection of Deflection-Based Inputs for the MEPDG

As with the traffic and environmental design inputs in the MEPDG, the material inputs are also based on a hierarchical level. One advantage of this approach is that it allows flexibility in selecting an engineering approach based on project size, cost, and importance.⁽¹⁾ The hierarchical levels for characterizing materials, in general, include the following:

• Level 1: Determination of material properties/parameters using both field and laboratory testing.
• Level 2: Estimation of material parameters using correlations with other material properties.
• Level 3: Estimation of material parameters based on experience with little or no testing.

For a given project, the designer may select a mix of hierarchical levels. The mix of hierarchical levels is possible because the MEPDG uses the same computational algorithm for estimating damage, regardless of the input design level.

In the MEPDG, deflection-based input data are primarily for the level 1 evaluation and generally consist only of the layer parameters; most of the other uses of deflection data are not incorporated into the design procedure, at least not directly.⁽¹⁾ In addition, the backcalculation results are not necessarily used directly as inputs in the MEPDG procedures but often require the application of adjustment factors to correspond to the laboratory-based values that were used in the development of the MEPDG performance models.

Project Evaluation in the MEPDG

The MEPDG provides information regarding the type of activities that should be conducted as part of a project evaluation; a general discussion is provided in section 10 of the AASHTO Mechanistic-Empirical Pavement Design Guide—A Manual of Practice (Interim Edition), and a more detailed discussion for the different pavement types is provided in section 3.⁽²⁾ Table 27 summarizes the input data for the three data levels. The discussion in the following subsections presents a brief summary of the primary evaluation activities and how they relate to interpreting deflection data.

¹All relevant surveys (e.g., visual, drainage). Levels 1 and 2 are typically benchmark data, while level 3 consists of a limited form of benchmark data obtained from windshield surveys and historic data.
IRI = International Roughness Index.
FN = friction number.

Pavement Condition Evaluation

A pavement condition evaluation is generally associated with a visual survey of the pavement surface in which pavement distresses are identified and quantified. Pavement distress surveys can be performed in conjunction with FWD testing to identify areas where more intensive testing may be beneficial and can also prove useful in evaluating variations in the deflection testing results (e.g., an area of higher than average deflections may correspond to an area with more distress). In addition, surface distress data are used to determine several qualitative adjustments to material parameters for rehabilitation design.

Although distress data are used in establishing a number of inputs in the MEPDG, they are not significantly used in level 1 and deflection data analysis. However, the distress survey data are used for level 3 rehabilitation design to determine the adjustment factor applied to the moduli for chemically stabilized (see table 28), HMA (see table 29), and PCC (see table 30) layers.

¹ Percent slabs cracked with all severities and types of cracks plus any repairs.
² Percent area, including repairs or patches, deteriorated joints, and deteriorated cracks (deteriorated joints and cracks converted to repair areas).
³ Percent area includes repairs, patches, and localized failures and punchouts converted to repair areas.
JRCP = Jointed reinforced concrete pavement.

Pavement Coring

A critical input in the backcalculation process is accurate layer thickness information. Although project documents, such as as-built drawings, are often the source of layer thickness information, coring the pavement to obtain in-place thicknesses is often the preferred alternative. As indicated in ASTM D5858, “Standard Guide for Calculating In Situ Equivalent Elastic Moduli of Pavement Materials Using Layered Elastic Theory,” bound pavement layer thicknesses should be reported to the nearest 5 mm (0.2 inches), and unbound pavement layer thicknesses should be reported to the nearest 25.4 mm (1.0 inch).⁽⁶⁶⁾

The number and location of cores is project specific and depends on several factors. Table 27 indicates that cores should be retrieved at intervals less than 600 m (2,000 ft) for the level 1 evaluation and at intervals greater than 600 m (2,000 ft) for the level 2 evaluation. Because of the differences in pavement cross section, pavement materials, construction dates, traffic levels, and many other variables, projects will often be split into multiple sections for analysis. As a minimum, it is generally recommended to retrieve at least one core sample from each analysis section.

Subsurface Boring

Subsurface borings identify the thickness of subgrade strata and provide material samples for laboratory testing (e.g., depth and thickness of subgrade soils, depth to water table or wet layers, depth to stiff layer, moisture content, density, and resilient modulus) and soil classification. Subsurface information important to the backcalculation of deflection data includes the depth to the rigid layer and the depth to the water table, if present. As a matter of convenience, subsurface borings are commonly performed at the same locations as coring. However, borings are also commonly conducted in unpaved areas adjacent to the pavement to avoid traffic closures; these locations may not provide information as accurate as would be obtained from directly under the pavement.

Laboratory Testing

The MEPDG requires design inputs from several laboratory tests, including testing to adjust input values derived from backcalculation.⁽¹⁾ Laboratory testing of the existing paving and subgrade materials is also a means to check or validate backcalculation results, which is highly recommended. Although the details of the tests themselves are not discussed here, the following list of the general layer parameters (or those required by the MEPDG) can be obtained from material samples:

• Existing HMA pavement: Unit weight, dynamic modulus, volumetric characteristics (air voids, asphalt content, gradation, and asphalt viscosity).
• Existing PCC pavement: Unit weight, elastic modulus, compressive or indirect tensile strength, and coefficient of thermal expansion.
• Existing stabilized layers: Elastic or resilient modulus, as appropriate for material.
• Unbound base/subgrade: Gradation, Atterberg limits, dry density, moisture content, and resilient modulus.

In the MEPDG, level 1 evaluation of JPCP recommends cutting and testing prismatic beams from pavement, while compression strength testing of cores is recommended for level 2.⁽¹⁾ For CRCP evaluation, the MEPDG recommends split tensile strength testing. Retrieving beam samples is often cumbersome and costly. In addition, split tensile testing has often been preferred for correlating PCC flexural strength from core specimens; therefore, it is also recommended for validating backcalculation results.

Other Project Testing

As described previously, other testing procedures often employed in a project evaluation include GPR, seismic testing methods, and DCP testing. GPR is becoming a more common test method in project evaluations and, as discussed in the MEPDG, its primary use in conjunction with deflection testing is in the determination of pavement layer thicknesses.⁽¹⁾ Unlike pavement coring, which provides thickness information for a relatively limited number of locations, GPR can produce continuous thickness data over the length of the project, including the exact location of the FWD test locations. The determination of pavement thickness using GPR has been reported to be accurate within a range 3 to 5 percent for new asphalt, 5 to 10 percent for existing asphalt and for concrete layers, and 8 to 15 percent for a granular base layer.⁽⁶⁷⁾

Seismic methods, such as SASW, IE, and IR, have been used to determine layer moduli and thicknesses. Use of these methods is growing but they are not yet as commonly used as some of the other field-testing procedures.

DCP testing is an acceptable input for the MEPDG for levels 2 and 3 with correlations to the necessary design inputs.⁽¹⁾ While it is not directly required for interpretation of backcalculation results, it can be used to help validate backcalculation and laboratory test results because it provides an indicator of the relative strength of unbound bases and subgrade materials (typically in terms of the California Bearing Ratio, which can be correlated to resilient modulus).

MEPDG Flexible Pavement Inputs

The required material parameters for HMA pavements in the MEPDG relevant to the use of FWD data and backcalculation results are the following:⁽¹⁾

• Time-temperature dependent dynamic modulus, E*, for the HMA layer(s).
• Resilient moduli for the unbound base/subbase and subgrade materials.
• Elastic modulus of the bedrock layer, if present.

The MEPDG also provides an option for considering nonlinear material parameters for the unbound layers for level 1 analysis.⁽¹⁾ However, the performance models used in the software have not been calibrated for nonlinear conditions, so this option is not considered further.

HMA Materials

The level 1 design analysis in the MEPDG software uses an E* (dynamic modulus) master curve and therefore does not accept a constant modulus value for the HMA layer(s).⁽¹⁾ This is necessary because the program calculates different HMA moduli for the different sublayers comprising the HMA layer(s) as a function of depth, speed, and axle type, as explained in appendix CC of the MEPDG.⁽¹⁾ However, the current MEPDG procedure (level 1) does allow static backcalculation of layer moduli for the rehabilitation of existing HMA pavements, which leads to constant backcalculated modulus for all layers, including the HMA layer. In this case, to maintain compatibility of the backcalculated layer moduli with the forward analysis in the software, the MEPDG procedure adjusts the HMA dynamic modulus (predicted E* based on input mixture properties) using the damage factor, d_j, which is the ratio of backcalculated HMA modulus to the predicted E* value using the Witczak equation. This effectively shifts the undamaged master curve down while essentially maintaining the variation with frequency as predicted by the Witczak equation. The procedure also calls for adjusting the master curve using the aged viscosity value in the predictive E* equation, which shifts the master curve upward; however, this upward shift is negligible compared with the downward shift using the backcalculated modulus for the damaged HMA layer, E_dam.

The procedure for determining the field-damaged dynamic modulus master curve is illustrated in figure 50.^(1).

©AASHTO. Used by permission.

Figure 50. Diagram. Illustration of HMA modulus correction.⁽¹⁾

The following steps summarize the procedure:

1. Conduct FWD testing in the outer wheelpath over the project to be rehabilitated (include cracked and uncracked areas); calculate the mean backcalculated HMA modulus, E_dam (combining layers with similar materials); record the HMA layer temperature at the time of testing; and determine the layer thickness along the project using coring or GPR.
2. Determine the mix volumetric parameters (air void content, asphalt content, and gradation), asphalt viscosity parameters (regression intercept (A), and regression slope of viscosity temperature susceptibility (VTS)) from field cores; follow the same procedure for determining binder viscosity-temperature properties as for a new or reconstruction design.
3. Develop an undamaged dynamic modulus master curve using the data from step 2 at the same temperature recorded in the field and at an equivalent frequency corresponding to the FWD pulse duration. The equation for the undamaged dynamic modulus is shown in figure 51.

Figure 51. Equation. Undamaged dynamic modulus.

Where:

E* = Dynamic modulus (MPa (lbf/inch²)).
δ, α = Fitting parameters that are dependent on aggregate gradation, binder content, and air void content; δ represents the minimum value of E* and δ+α represents the maximum value of E*.
β and γ = Regression parameters that are dependent on the characteristics of the asphalt binder and the magnitude of δ, α.
t_r = Time of loading at reference temperature (s).

4. Estimate the damage by solving for the fatigue damage in the HMA layer, d_ac, in the equation in figure 52.

Figure 52. Equation. Estimate of damaged modulus.

Where:

E*_dam = Damaged modulus, lbf/in² from step 1.
δ = Fitting parameters that are dependent on aggregate gradation, binder content, and air void content; represents the minimum value of E*.
E* = Undamaged modulus, lbf/inch² from step 3.

5. Determine α' as shown in figure 53.

Figure 53. Equation. Determination of α'.

6. Determine the field master curve using α' in the equation in figure 51 instead of α. It is also important to consider the reduced time representative of the nondestructive testing (NDT) loading and viscosity temperature at the time of the NDT. This is incorporated into the determination of the field master curve using the equations shown in figure 54.

Figure 54. Equation. Determination of the field master curve.

Where:

t_r = Reduced time for NDT loading (s).
t = NDT loading time (s).
η = Binder viscosity at the NDT temperature.
η_Tr = Binder viscosity at 21°C (70 °F).
η = Binder viscosity.
A = Viscosity temperature susceptibility intercept.
VTS = Viscosity temperature susceptibility slope.
T_r = Temperature (° Rankine).

For levels 2 and 3 analyses, no FWD testing is required. The level 2 procedure is similar to the level 1 procedure in that field cores are used to obtain the undamaged modulus; however, estimates for fatigue damage of the existing asphalt layer are determined through a detailed pavement condition survey and the calibrated MEPDG distress models. For example, the equation in figure 55 illustrates the distress model for top down cracking.

Figure 55. Equation. Distress model for top-down cracking.

Where:

FC_top = Percent top-down cracking in the asphalt layer.
C₁ ,C₂, C₄ = Regression coefficients.
damage = Damage in the HMA layer.

The equation in figure 55 is solved for the damage term, which is then used in the equation in figure 52 to determine the damaged modulus master curve.

For the level 3 procedure, no coring or testing is required; instead typical estimates of HMA mix parameters (typical volumetric and binder properties) are input, and the program calculates the undamaged master curve. The damage factor is estimated from general condition data previously presented in table 29, and the damaged modulus master curve is then determined using the equation in figure 52.

Chemically Stabilized Materials

Similar to unbound materials, only level 1 analysis calls for FWD testing in rehabilitation and reconstruction designs. The moduli for any chemically stabilized layer (including lean concrete and cement stabilized base, as well as lime/cement/fly ash stabilized soils) can be either determined in the laboratory or backcalculated using standard backcalculation procedures. Layer thicknesses can be obtained by coring or using NDT techniques such as the GPR. The MEPDG recommends performing limited testing on cored lime stabilized soil specimens to verify/confirm the backcalculated values and notes that backcalculation of modulus values for layers less than 150 mm (6 inches) thick located below other paving layers may be problematic, thus requiring laboratory testing.⁽¹⁾

For a level 1 characterization, the modulus at the current damage level, E_CTB, and the intact modulus are used to determine a damage factor. The modulus at the current damage level is the value obtained from backcalculation. The intact modulus is obtained from the compressive strength of intact cores removed from undamaged areas of the pavement and is used to estimate the initial intact modulus, E_max (described in part 2, chapter 2 of the MEPDG).⁽¹⁾ With E_CTB and E_max known, the current damage level can be determined, as illustrated in figure 56.

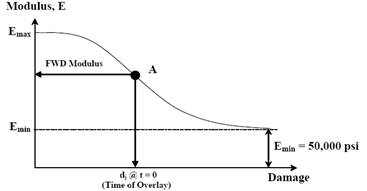
© AASHTO. Used by permission.

Figure 56. Graph. Illustration of estimating damage factor using backcalculated base moduli.⁽¹⁾

The backcalculated modulus is used as the modulus at the beginning of the overlay analysis and further reduced based on the condition of the stabilized layer and pavement surface (as shown by the equation in figure 57).

Figure 57. Equation. Reduction of backcalculated modulus based on observed conditions.

Where:

C_CTB = Percent alligator cracking in the chemically stabilized layer.
C_s = Percent alligator cracking observed at the pavement surface.
RC = Percent of cracks reflected, percent (, where t = time (yr) and a and b = fitting parameters).

For level 2 analysis, correlations with strength test data (see table 11-6, AASHTO Mechanistic-Empirical Design Guide—A Manual of Practice (Interim Edition) are used.⁽²⁾ For level 3, the MEPDG calls for estimating the moduli based on experience or historical records and lists typical modulus values. The MEPDG also notes that semirigid cementitiously stabilized materials are more prone to deterioration as a result of repeated traffic loads when used in HMA pavements and suggests typical values (see table 31) for such deteriorated materials.

Unbound Materials

In the case of unbound materials, FWD testing in rehabilitation and reconstruction designs is required only in a level 1 analysis. The modulus for each unbound layer (including the subgrade) can be either determined in the laboratory using cyclic triaxial tests or backcalculated using standard backcalculation procedures. As discussed previously, while the MEPDG does allow for the generalized nonlinear, stress-dependent model in the design procedure, this approach is not recommended at the time of this report because the performance models in the software have not been calibrated for nonlinear conditions; therefore, the option of backcalculating the k₁, k₂, and k₃ parameters in the nonlinear model is not discussed. Consequently, the discussion only includes the backcalculation and use of effective moduli that account for any stress sensitivity, cracks, or any other anomalies in any layer within the existing pavement.

As with the HMA modulus, the backcalculated values must be adjusted to correspond with laboratory-obtained values, on which the MEPDG forward designs are based. Although there is continued debate within the pavement community on appropriate correlation values, the existing correlations are recommended until more definitive guidance can be established. Part 3 of chapter 6, of the MEPDG indicates that adjustment factors of 0.40 for subgrade soils and 0.67 for granular bases and subbases have been used to correlate backcalculated moduli.⁽¹⁾ The MEPDG also provides additional backcalculation adjustment guidance for different layers, as summarized in table 32.

E_R = Backcalculated elastic modulus.
M_R = Elastic modulus of the in-place materials determined from laboratory repeated load resilient modulus test.

For level 2 analysis, correlations with strength test data are used. For level 3, the guide lists typical modulus values based on soil classification but warns that they are approximate and strongly recommends some form of field testing.⁽¹⁾

Feasibility of Using Dynamic Backcalculation for Future Versions of the MEPDG

Ideally, it should be possible to determine a curve of HMA layer modulus as a function of frequency using a (dynamic) frequency-based backcalculation algorithm. This would give a more direct estimation of the HMA layer modulus with frequency from actual field conditions as opposed to relying on a laboratory-derived curve such as the Witczak equation. However, care should be taken in interpreting and using such data with the existing MEPDG performance predictions, because these data have been calibrated using laboratory-derived moduli. Also, recent analyses show that while dynamic backcalculation methods can backcalculate layer moduli and thicknesses accurately from synthetically generated FWD data for pavement systems with three or more layers, some serious challenges arise when using field data.⁽³⁸⁾ The frequency-domain method can lead to large errors if the measured FWD records are truncated before the motions fully decay in time, which leads to corruption of the frequency content of the signal; the only remedy is to match the sensor time histories in the time domain. However, FWD-measured time histories may not be accurate enough in this regard, because data beyond the first peak include an unknown amount of signal drift coming from the double integration of acceleration measurements (or the single integration of velocity measurements) to obtain deflections.

Dynamic, time-domain backcalculation algorithms present another challenge in that they cannot directly determine the HMA modulus as a function of frequency. Such algorithms either assume a constant HMA modulus under linear elastic behavior (similar to many static backcalculation procedures) or use a prescribed function of the HMA layer modulus with frequency (e.g., linear relation in the log-log space).

Rigid Pavement Inputs in the MEPDG

The input parameters needed for the design of an overlay on top of a PCC pavement using the MEPDG that can be extracted from FWD data include the following:

• Elastic modulus of the existing PCC and base layers.
• Subgrade k-value.
• PCC flexural strength (based on the backcalculated PCC elastic modulus).

The moduli for each layer can also be backcalculated using layered elastic theory, but as previously discussed, it is better to define the stiffness of the lower layers with the backcalculated k-value. Although not a direct input into the MEPDG, the deflection data should also be used to identify any voids present beneath the slab because the design analysis assumes that any voids will be addressed before the overlay is placed. Recommendations to consider when determining these inputs, based on FWD data, are provided in the following sections.

Effective k-Value

The ideal method for characterizing the subgrade in the MEPDG is by backcalculating the effective k-value, which represents the stiffness of all layers beneath the base. It is important to note that the input k-value in the MEPDG for rehabilitation design is the backcalculated dynamic value, not the typically corrected static k-value. (Note that traditionally, an effective k-value refers to a k-value that is adjusted for seasonal effects, and the composite k-value refers to the composite stiffness of all layers beneath the slab.) In addition to the dynamic k-value, the MEPDG also requires that the moduli of each layer be provided; this is because the k-values are used for PCC stress calculations and the layer modulus values are used for calculation of the strains in an HMA overlay (placed as a rehabilitation treatment).⁽¹⁾

When the layer moduli are used to define the characteristics of the pavement structure in the MEPDG for new PCC pavement designs, the software uses an internal conversion process to determine an effective k-value. The MEPDG documentation defines an effective k-value as the composite stiffness of all layers beneath the base, as shown in figure 58. The process involves backcalculating the effective k-value from the theoretical deflection basin produced using the elastic layer program JULEA. However, in this process, the subgrade resilient modulus is adjusted to reflect the lower deviator stress under PCC pavements (compared with that used in laboratory resilient modulus testing) before generating the deflection basin. Therefore, the subgrade resilient modulus backcalculated from FWD testing cannot be used directly in the MEPDG for PCC or composite pavements because the backcalculated moduli values reflect the state of stress under PCC pavements and not under laboratory testing conditions. While adjustments could be made to obtain “laboratory” resilient moduli, the k-value directly backcalculated from the FWD data best represents the true foundation stiffness. Therefore, backcalculation procedures that directly produce k-values are recommended for PCC pavements.

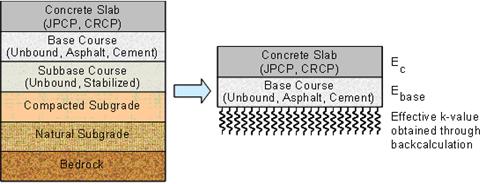
©AASHTO. Used by permission.

Figure 58. Diagram. Illustration of the E-to-k conversion process incorporated in the MEPDG.⁽¹⁾

The dynamic k-value for rehabilitated pavements can be backcalculated from PCC surface deflections.⁽²⁾ Therefore, the result is an effective dynamic k-value that represents the compressibility of all layers beneath the PCC slab, in which the PCC slab is defined as follows based on the proposed rehabilitation strategy:

• For unbonded JPCP/CRCP over an existing rigid pavement, the PCC slab is defined as the PCC overlay.
• For bonded PCC over JPCP/CRCP, the PCC slab is the composite of the overlay and existing PCC layer.

In the case of an HMA overlay over JPCP, the MEPDG documentation (part 3 of chapter 6) states that the HMA/JPCP structure would be converted to an equivalent structure that consists of an equivalent slab and a foundation.⁽¹⁾ The stiffness of the equivalent slab is determined by the stiffness of the HMA overlay, the existing PCC layer, and the base layer. The effective dynamic k-value is used to represent the compressibility of the subgrade layer only.

To better illustrate these definitions, the research team generated three figures—one for each overlay rehabilitation type. Figure 59 through figure 61 present how the actual structure of the rehabilitated pavement is converted into an equivalent layered system to calculate the effective dynamic k-value for HMA, unbonded PCC, and bonded PCC overlays, respectively. As shown in these figures, the meaning of the effective dynamic k-value varies with the type of rehabilitation, as described in the following subsections.

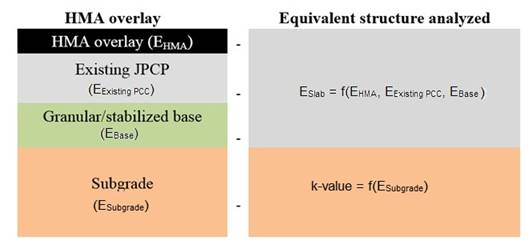
Figure 59. Diagram. Transforming the actual pavement structure into an equivalent structure for an HMA layer over a PCC slab.

Figure 60. Diagram. Transforming the actual pavement structure into an equivalent structure for an unbonded JPCP/CRCP over a PCC slab.

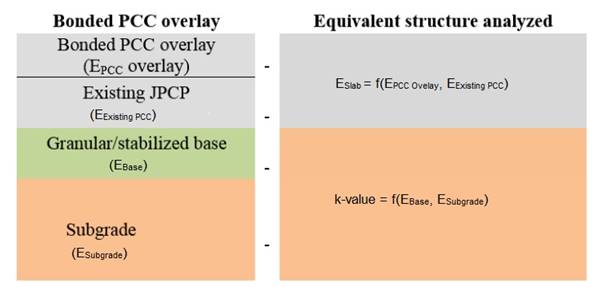
Figure 61. Diagram. Transforming the actual pavement structure into an equivalent structure for a bonded JPCP/CRCP over a PCC slab.

HMA Overlay

The k-value input does not appear to be used within the MEPDG for HMA overlay design; therefore, it is suggested that the k-value not be entered at this time.

Bonded PCC Overlay

For bonded PCC overlays, the MEPDG k-value input represents the composite stiffness of all layers below the base. The backcalculated k-value can be used directly to define this input if the existing slab is on a stabilized base. However, in reality, the backcalculated k-value represents the stiffness of the base as well as all other underlying layers if the base is not stabilized. The backcalculated k-value can be adjusted to negate the stiffness of the base by using the method proposed in the Portland Cement Association (PCA) design guide, which combines the stiffness of the subgrade and the subbase.⁽⁶⁸⁾

The elastic modulus of the base must also be established for the bonded overlay. It is suggested that a typical value be used if the base in unstabilized. If the base is stabilized, then the method presented by Ioannides and Khazanovich can be used to modify the backcalculated elastic modulus of the PCC and used to estimate the base layer modulus.⁽⁶⁹⁾

Unbonded PCC Overlay

As shown in figure 57, the k-value defined by the MEPDG consists of the composite stiffness of all layers below the HMA debonding layer.⁽¹⁾ At the time of this report, it was not possible to backcalculate a k-value representing the combined the stiffness of the complete pavement structure, including the slab. It was found that for the limited cases evaluated, reasonable overlay thicknesses were achieved when the k-value representing the stiffness for all layers beneath the slab was used, as described for the bonded overlay design. Therefore, this approach is suggested until more definitive guidance can be provided.

Finally, it is important to correctly enter in the other material characterization properties, such as the gradations of these layers, because this information is used along with EICM to estimate the seasonal effects on the k-value. When entering the k-value, the designer must also enter the month in which the k-value was measured. Seasonal corrections are then applied to the k-value based on the seasonal moisture conditions predicted through the EICM.

PCC Overlay of HMA Pavements

The above discussion focused on PCC overlays of PCC pavements, but the k-value for the design of PCC overlays over HMA pavements must also be considered. Although the MEPDG documentation does not provide clear information on how the structure is modeled, it appears that based on a limited parametric study, the composite-k-value consists of all layers below the existing HMA pavement. The transformation of the actual pavement structure into an equivalent pavement structure used in the analysis is shown in figure 62. Because a valid method was not available at the time of this report for backcalculating the k-value of an existing HMA pavement, it is recommended that the elastic modulus of each layer be backcalculated as described above for flexible pavements.

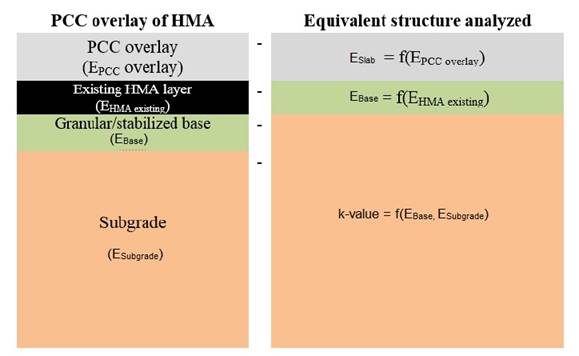
Figure 62. Diagram. Transforming the actual pavement structure into an equivalent structure for a PCC overlay of an existing HMA pavement.

PCC Parameters

The elastic modulus of the existing slab must be determined for overlay designs and existing JPCP being considered for restoration. The elastic modulus can be determined by retrieving cores and measuring the chord modulus based on ASTM C469 or by using FWD data to backcalculate the modulus.⁽⁵⁵⁾ The MEPDG indicates a backcalculated modulus must be multiplied by 0.8 to convert it from a dynamic value to a static, elastic modulus. In addition, the elastic modulus determined either from backcalculation or laboratory testing must be adjusted to reflect the overall condition of the pavement (for unbonded overlays only). The procedure for using the backcalculated PCC elastic modulus for rehabilitation is summarized as follows:⁽¹⁾

1. Estimate the project mean PCC modulus, E_TEST, by backcalculation using the Best Fit method. Multiply this backcalculated value by 0.8 to arrive at a static elastic modulus for the uncracked PCC.
2. Determine the overall condition of the existing pavement according to the guidelines presented in part 2, chapter 5 of the MEPDG. Choose a pavement condition factor, C_BD, based on the existing pavement condition, as presented in the MEPDG and summarized in table 33 (and also described in table 30, presented earlier).

3. Calculate E_BASE/DESIGN = (C_BD)(E_TEST) to determine the design modulus input of the existing PCC slab.

The PCC flexural strength of the existing slab is also required for overlay design. As previously indicated, for JPCP, the MEPDG recommends prismatic beams be obtained from the existing pavement for level 1, while level 2 is based on relating core compressive strengths; for CRCP, indirect tensile strength is the required input. Although the MEPDG recommends retrieving beams for level 1 and correlating compression strength for level 2 for JPCP, the use of split tensile strength determined from cores and correlated to flexural strength is often the preferred method. For pavement restoration, the PCC elastic modulus is assumed not to increase over time because the strength and stiffness of mature concrete will not significantly change.

Composite (HMA/PCC) Pavement Inputs in the MEPDG

The MEPDG evaluates HMA/PCC pavements in two steps. First, the pavement system is analyzed as a rigid pavement to model continued cracking of the underlying PCC pavement. The HMA distresses are then modeled, including thermal cracking, fatigue cracking, and rutting, and overall IRI is also evaluated. Assuming that the analysis is conducted for a new HMA overlay, the key input parameters for this analysis obtained from FWD data are the subgrade k-value, the E_PCC, and the PCC modulus of rupture (based on backcalculated PCC modulus). The joint LTE is also used in reflection cracking prediction, but only qualitative results (good or poor) are used. At the time of this report, the MEPDG did not use the backcalculated HMA overlay modulus in the design structure.⁽¹⁾

The backcalculation results for HMA/PCC pavements may contain greater variability than those for other pavement types, largely because the data may reflect test points conducted over joints or cracks in the underlying PCC pavement. For valid results, the locations of the joints in the underlying pavement should be identified, and the testing should be performed at midslab. Any significant deviations from the representative values may be an indication that the testing was conducted too close to underlying cracks or joints, and those results should be excluded in determining the average k and E values. For the evaluation of the structural adequacy of the underlying PCC pavement, the elastic modulus determined over the intact portion of the slab is needed. However, those points may be an indication of an area of localized weakness and reveal the need for corrective action.

Effective k-Value

For rehabilitation design of HMA/PCC pavements, MEPDG allows entry of the backcalculated k-value directly. Both the dynamic k-value and month of testing are entered. However, the backcalculated k-value is treated as discussed above for rigid pavement rehabilitation design; the user is still required to enter resilient moduli for all unbound layers and subgrade. The MEPDG processes the input as usual (for new design) and determines the seasonal k-values based on EICM results using the E-to-k conversion procedure. If the backcalculated k-value is entered, the seasonal adjustment is made using the relative k-values obtained through the E-to-k conversion process as the scaling factors.

For the HMA analysis, the seasonal resilient moduli are used, but no adjustment is made to account for any difference between the k-value from the E-to-k conversion process and the backcalculated k-value. To ensure consistency between the backcalculated k-value and the resilient moduli used in the HMA analyses, an iterative procedure may be used to adjust the subgrade resilient modulus input, rather than simply entering the backcalculated k-value. This involves adjusting the input subgrade resilient modulus up or down to match the k-value from the E-to-k conversion process and the backcalculated k-value for the month of the FWD testing. If the backcalculated k-value is entered directly, there may be some discrepancy between the k-value used in the PCC analysis and the resilient moduli used in the HMA analysis; however, this minor discrepancy is not likely to have any significant effect on the predicted HMA overlay performance.

The evaluation of FWD data is perhaps more difficult for HMA/PCC pavements than for other pavement types because of the complications introduced by the compression of the HMA layer. On the other hand, the structural adequacy is not always the principal concern for HMA/PCC pavements. Placing even a relatively thin layer of HMA (75 to 100 mm (3 to 4 inches)) can greatly reduce the critical stresses in the underlying PCC pavement for the following reasons:

• Additional stiffness provided by the HMA overlay. The HMA overlay bonds to the PCC layer to provide a significant increase in the structural capacity.
• Significant reduction in temperature gradients. On PCC pavements, the curling stresses can make up more than 50 percent of the combined stresses during the critical periods when the pavement is subjected to high temperature gradients (positive or negative). The most severe temperature changes occur within the top 75 mm (3 inches) of the pavement. The placement of an HMA overlay significantly reduces the magnitude of the temperature gradients.
• Reduction in contact pressure. The HMA layer reduces the contact pressure on PCC pavement by spreading the load over a larger area.

The combined effect of these factors is that the critical stresses in the PCC pavement drop to a fraction of those occurring before overlaying, even for a 75-mm (3-inch) HMA overlay. Thus, the performance life of HMA/PCC is typically governed by material and functional factors, not structural failure of the underlying PCC pavement. The key distresses include rutting, reflection cracking, and deterioration of the reflected cracks. The structural evaluation of HMA/PCC pavements is primarily a design check to ensure that the stresses are well within the tolerable limits. Therefore, the backcalculation procedure for HMA/PCC does not need to be as comprehensive.

PCC Parameters

The PCC parameters discussed above for rigid pavements also apply to composite pavement structures. However, the difficulty with composite pavements is that the condition of the PCC pavement is not readily visible because of the presence of the existing overlay. Judgment needs to be applied using backcalculated modulus results, existing surface conditions, and historical performance data, to determine an appropriate overall condition of the underlying PCC.

Other Uses of Deflection Data in the MEPDG

The following briefly describes the use of other deflection data within the MEPDG.

LTE

As mentioned previously, LTE is not a direct input in the MEPDG procedure. However, it is used to establish qualitative measures for rehabilitation design. Table 34 summarizes the qualitative ratings based on the determined LTEs from deflection testing.

Void Detection

There is no direct input in the MEPDG to characterize the uniformity of the support conditions beneath the slab. However, it is important to perform FWD testing to detect the presence of voids because the MEPDG design procedure assumes that any voids present will be repaired before the placement of an overlay.

MEPDG Inputs for Evaluation of Existing Pavement Layers

As provided in the MEPDG Manual of Practice, table 35 provides a summary of suggested steps for assessing the existing pavement structure.⁽²⁾ Not all suggested steps are required, and the required level of investigation, evaluation, and testing should be based on the knowledge and experience of the design engineer.

Summary

This chapter summarizes mechanistic-empirical pavement design principles, provides an overview of the MEPDG, and summarizes inputs (including deflection data) for use in the MEPDG for the design of rehabilitated pavements. Specifically related to the use of deflection data, table 36 summarizes how deflection data can be used within the MEPDG (applicable for level 1 inputs only).