U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| TECHBRIEF |
| This techbrief is an archived publication and may contain dated technical, contact, and link information |
| Publication Number: FHWA-HRT-13-093 Date: December 2014 |
Publication Number: FHWA-HRT-13-093 Date: December 2014 |
PDF files can be viewed with the Acrobat® Reader®
FHWA Publication No.: FHWA-HRT-13-093 |
The Long-Term Pavement Performance (LTPP) database contains surface profile data for numerous pavements that are used mainly for computing International Roughness Index (IRI).(2) In order to obtain more information from these surface profiles, a Hilbert-Huang Transform (HHT) based surface profile algorithm was developed to analyze LTPP field road profile data in order to extract smoothed, consistent profiles from noise-filled data sets using empirical mode decomposition (EMD). The application of this algorithm to concrete surface profiles resulted in the successful separation of the intrinsic mode functions contained within the profile data for several LTPP pavement test sections from Wisconsin, Arizona, and Utah. Arizona was the only test section where the profiles showed consistent "curl" deflections for the same slab over a 20-month timespan and during both winter and early fall seasons. The consistent slab shape is likely due to built-in curl. Built-in curl is defined as permanent concrete slab deformation that occurs early in the life of the pavement.
By categorizing and separating intrinsic mode functions contained within LTPP profile data, the results can be used to analyze specific portions of LTPP surface profile data in order to improve concrete pavement models in the future. Currently, no comprehensive procedure exists to model or estimate long-term, effective built-in curling. The developed surface profile algorithm that has proven to be universal can be applied to any LTPP profile data for analysis.
The LTPP database contains surface profile data for pavement sections throughout the United States that is used to compute IRI. Byrum previously used Wisconsin LTPP section profiles to analyze curvature in concrete pavement slabs.(3) However, the difficulty with analyzing raw field profiles is the level of noise and frequency of inconsistencies within these data sets. To remedy this problem, an automated pavement analysis method was developed to smooth the real-field profiles and allow for more accurate and consistent analysis of pavement sections or slabs. This method is based on the EMD process contained within the HHT. Past analysis of road surface profiles using the HHT is limited. Adu-Gyamfi et al. used the empirical mode decomposition for pavement surface analysis, and Attoh-Okine et al. also used it to analyze two flexible pavement profiles.(4,5)
The application in this paper focuses on grouping intrinsic mode functions (IMF) to analyze built-in curl features of rigid pavement profiles. Extraction of noise in real-life and artificial profile data can be performed by applying a sifting process to filter and identify the IMFs that are contained in raw surface profiles. The idea behind the Hilbert-Huang-based sifting process is to identify the intrinsic functions contained within the data and to subsequently remove and categorize them in order to analyze specific portions of the original profile. Figure 1 shows the basic decomposition of any profile.(6)
Figure 1. y of x is equal to the summation of a c subscript j of x plus r subscipt n of x.
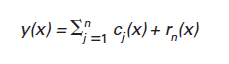 |
| ©Dan Franta |
Where y(x)L is the original profile, cj(x) represents IMFs within the data set, and rn(x) is the residue after the first n IMFs have been removed.
In the case of pavement profiles, some of the IMFs are due to "noise/surface texture," "curling," and/or "base trends" within the pavement. Removing the IMFs due to "noise/surface texture" from the distorted, non-linear profiles, will reveal the smoother functions of the original data set that can be attributed to "curl" and/or "base trends." Quotations are used around "noise/surface texture," "curl," and "base trends" to emphasize that these terms are used only to group functions of similar characteristics contained in surface profiles. Surface profiles contain IMFs attributed to many different variables. The goal of this paper is not to explain what causes trends in pavement profiles but to develop a method to analyze them.
After the automated profile analysis is performed, the resulting IMFs can be grouped to represent different portions of the original data set. Based on frequencies and wavelengths of the extracted functions, IMFs will be categorized into three separate groups. Frequencies of the intrinsic mode functions decrease as the number of calculated IMFs increase. Therefore, the first IMF extracted will have the highest frequencies and shortest wavelengths of any function within the profile. The opposite will be the case for the final IMF.
The first group, "noise/surface texture" functions (NFUN), are high frequency IMFs resulting partially from surface texture or noise contained within the pavement profile. The wavelengths are short and the amplitudes small. The peaks of the waves tend to appear sharp and pointed.
"Curl" functions (CFUN) compose the second group. Compared to the NFUNs, these IMFs are characterized by lower frequencies, higher amplitudes, and longer wavelengths. Before CFUNs are extracted, much of the "noise/surface texture" will have already been removed from the profile by the NFUNs. This will cause the CFUNs to appear smoother than the NFUN group. The hypothesis used here is that these IMFs are partially caused by temperature curling or built-in curling within the pavement slabs.
The last group, "base" functions (BFUN), display the lowest frequencies, and the wavelengths will be longer than the CFUNs. The BFUNs are due to overall "base trends" within the profile. In ISLAB2005 concrete slab models, the curling magnitude is always calculated assuming the original surface is horizontally flat. This is not the case for a real pavement section. If the underlying "base trends" of pavement are not taken into account, there will likely be deflections and curvatures that are incorrectly assumed to be caused by "curling." The BFUNs are the smooth, low frequency IMFs. The final residue is always grouped with the BFUNs.
Grouping IMFs allows for evaluation of any portion of the profile, both individually and as a group. For instance, the overall "base trend" of a profile can be obtained by summing all the members of the BFUN group. In most cases, the portion of greatest interest is the removal of the NFUN group to reveal the smoother characteristics of the slab profiles in absence of distortions from "noise/surface texture," leaving just the combination of the CFUN and BFUN groups representing a smoothed version of the profile.
Grouping IMFs can be difficult because there is no clear or concise method by which to do it, and profiles contain varying numbers of IMFs. Steps for the classification of the IMFs and their grouping into NFUNs, CFUNs or BFUNs, previously defined, is described below using an LTPP pavement section from Wisconsin.
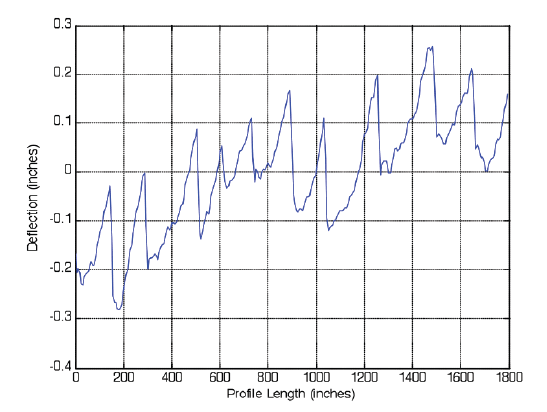
The LTPP database contains a profile for Wisconsin pavement section 553009 (see figure 2). This profile was collected on June 9, 2008, during run 6, at 4:07 p.m. from the left wheel path. The 11-slab section contains concrete that is 8 inches thick. The profile was chosen because the slab profiles are easily identified by their surface data and provide a good example of classifying IMFs.
The developed automated Hilbert-Huangbased algorithm was applied to the entire profile shown in figure 2, and the IMF results for the middle slab (centered on x ≈ 800 inches) were extracted for analysis. When using this automated profile analysis algorithm with field data, spiking effects during the empirical mode decomposition process tend to cause distortions near the edges of the analyzed profiles. The middle slab is extracted for analysis to avoid these distortions.
Figure 2. Original 11-slab profile from Wisconsin LTPP test section 553009.
 |
| ©Dan Franta |
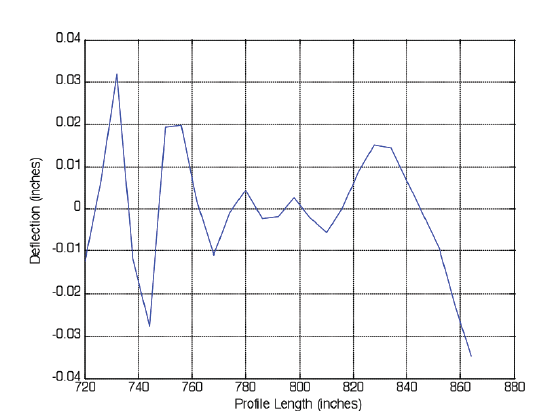
The first IMF, and member of the NFUN group, is composed of "noise/surface texture" from the original profile. Figure 3 shows a function with the characteristic high frequencies and short wavelengths of members of the NFUNs. Spiking and distortion did take place near the edges of the 11-slab profile during the decomposition process, but the profile was long enough that the middle slab was unaffected.
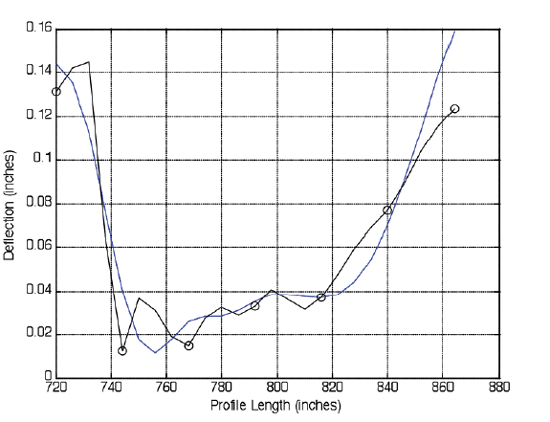
Removing the first IMF from the original profile leads to the smoother profile (referred to as the first residue) as shown in figure 4. It is clear that the first IMF is indeed a function of the NFUN group. There is some noticeable smoothing near the bottom of the slabs, meaning the empirical mode decomposition sifting is performing as expected. The amount of data, still present within the first residue which shows characteristics of "noise/surface texture," will determine whether the second IMF is grouped as an NFUN or a CFUN. There appears to still be "noise/surface texture" contained within the first residue as shown in figure 4. Therefore, the second IMF will likely be another member of the NFUN group.
Figure 3. First IMF from the middle Wisconsin LTPP 553009 slab profile.
 |
| ©Dan Franta |
Figure 4. First residue with the original profile from Wisconsin LTPP test section 553009.
 |
| ©Dan Franta |
The second IMF, shown in figure 5, still displays the short wavelength and high frequency characteristics of "noise/surface texture." Although the second IMF has longer wavelengths and lower frequencies than the first IMF, the frequencies and wavelengths displayed are not characteristic of "curling." Therefore, the second IMF will be classified as another NFUN.
Removing the second IMF from the first residue gives the resulting second residue shown in figure 6. The remaining "noise/surface texture" portions of the original profile have been significantly removed by the second IMF, as displayed by the smoothness of the second residue. Now that the "noise/surface texture" has been extracted, the next IMF will likely be composed of "curl."
Figure 7 shows the portion of the original profile resulting from "curl" and classified as a member of the CFUNs. It is clear that this IMF has lower frequency, smoother waves, and larger amplitudes than what was typical of the NFUNs. Notice that the "curl" data is zeroed on the x-axis. This is because the &quaot;curl" data is free of nearly all "base trends." Also, notice that "curl" is driven by joint spacing. The lengths of the slab correspond to the resulting "curl" wavelength. The third IMF appears to contain most of the "curl" data from the original profile; consequently, after it is removed, the original profile is reduced to its "base trends."
As previously mentioned, the third IMF (shown in figure 7) removed the "curl" data from the second residue (shown in figure 6). Removal of the third IMF from the second residue results in the third residue as shown in figure 8. The third residue displays the underlying "base trend" of the data set for the middle slab. Therefore, any remaining IMFs, along with the final residue, will be classified as BFUNs. IMFs four, five, and six, along with the final residue, compose the BFUN group for this Wisconsin slab as shown in figure 8. It is clear that the BFUN group is free of "noise/surface texture" and "curl."
Figure 5. Second IMF and second member of the NFUN group.
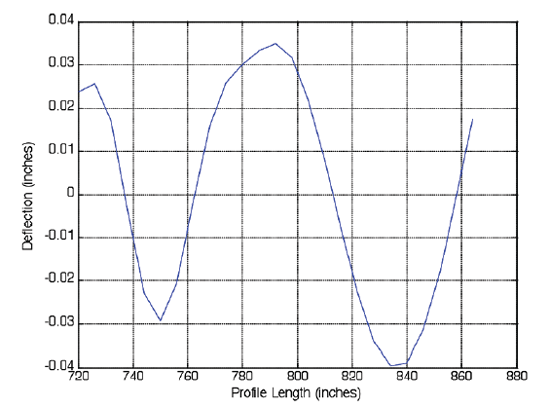 |
| ©Dan Franta |
Figure 6. Second residue with the original shifted profile.
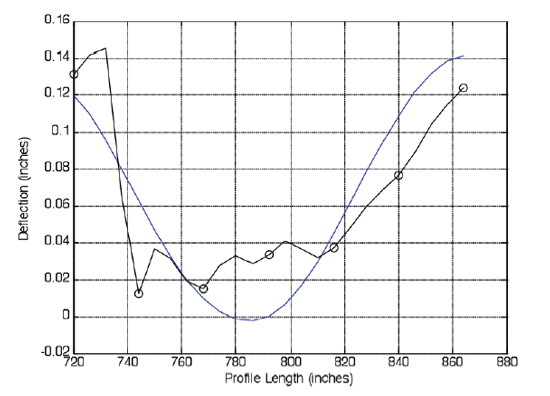 |
| ©Dan Franta |
Figure 7. Third IMF and first and only member of the CFUN group.
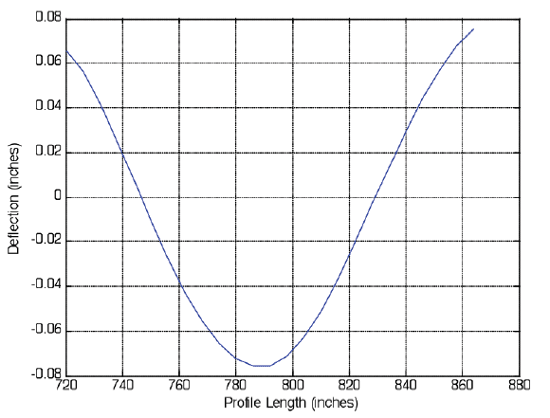 |
| ©Dan Franta |
Physical grouping of the IMFs can now be completed. The summation of the NFUNs is shown in figure 9. The CFUNs group is composed of the third IMF already displayed in figure 7. The BFUNs with the original slab profile are displayed in figure 8. Finally, the combination of CFUNs+BFUNs with the original profile is shown in figure 10. This final combination of the CFUNs+BFUNs constitutes a smoother version of the original slab profile.
The sum of the two IMFs comprising the NFUN group for this profile is shown in figure 9. The high frequency and low amplitude wavelengths, along with lack of smoothness, are consistent with trends associated with "noise/surface texture" and thus confirm these IMFs do indeed belong in the NFUN group.
Finally, as shown in figure 10, the BFUNs and CFUNs comprise the majority of a profile data set. The original profile was shifted downward over the top of the CFUNs+BFUNs result, using a minimization of least squares, in order for easier comparison of the two profiles. The CFUNs+BFUNs had a significant portion of the "noise/surface texture" removed, resulting in a smoother profile. NFUNs distort original profiles, therefore suggesting that the combination of the CFUNs+BFUNs is a more accurate representation of the profile the LTPP data were collected to explore.
Figure 8. Third residue with original shifted profile.
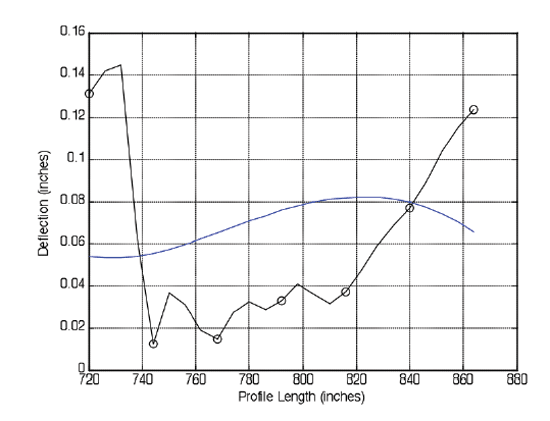 |
| ©Dan Franta |
Figure 9. NFUN group for the Wisconsin LTPP 553009 slab profile.
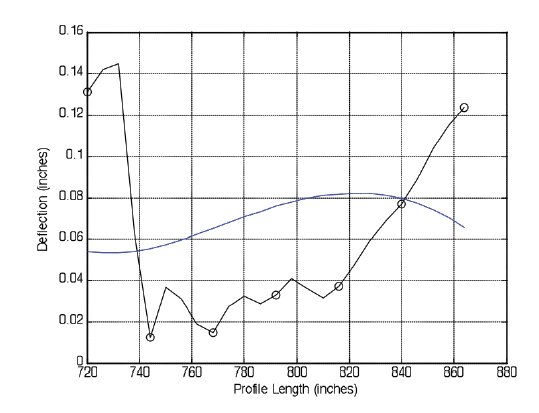 |
| ©Dan Franta |
Figure 10. CFUNs+BFUNs with the original slab profile (shifted by least squares minimization for comparison).
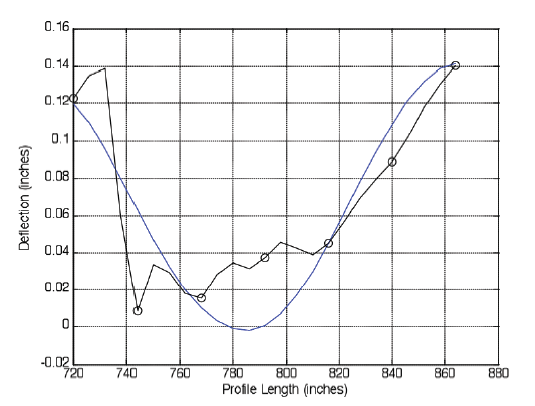 |
| ©Dan Franta |
Using the grouping of IMFs procedure from the Hilbert-Huang-based profile analysis algorithm as described, the results from its application to profiles from the Arizona and Utah LTPP test sections are provided. CFUNs+BFUNs results from surface profiles collected at different times from the Arizona test section are compared. A condensed version of the automated profile analysis results will be provided in this section.
The surface profile data from Arizona test site 040215 was used for the analysis. This test section contains profile data (from run 1) for eleven 15-ft-long slabs of 11-inch-thick concrete, collected January 25, 2010, at 5:37 p.m. The left wheel path data were used for analysis. The automated Hilbert-Huang-based profile analysis algorithm was applied to the entire profile shown in figure 11.
CFUNs+BFUNs analysis is used in the middle slab to avoid edge spiking effects from the sifting process.
The CFUNs+BFUNs group is nearly free of all "noise/surface texture" distortions as shown in figure 12.
The same test section was analyzed in a similar manner using profile data collected from run 2 on September 20, 2008, at 2:26 a.m. from the left wheel path.
The surface profile section displayed in figure 13 shares some similarities with the profile shown in figure 11.
Figure 11. Original Arizona LTPP 040215 profile collected January 25, 2010.
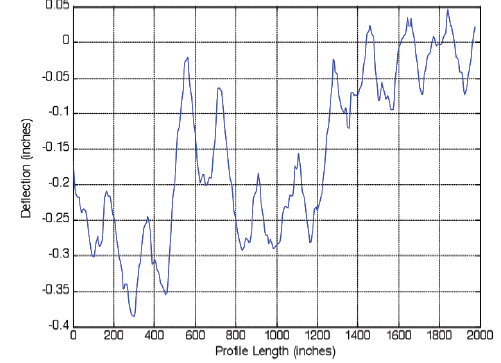 |
| ©Dan Franta |
Figure 12. CFUNs+BFUNs with the original middle slab profile from Arizona.
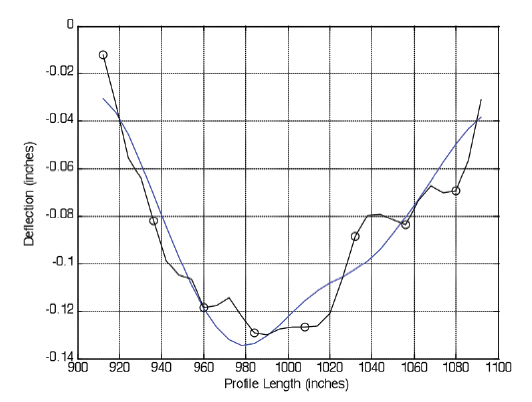 |
| ©Dan Franta |
Figure 13. The Arizona LTPP 040215 section collected September 20, 2008.
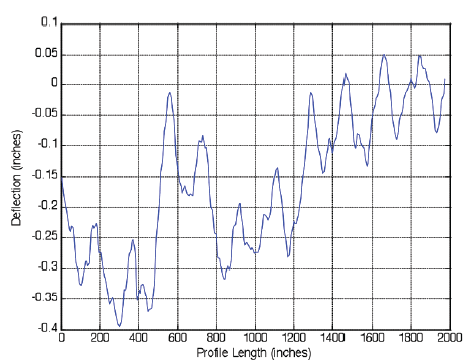 |
| ©Dan Franta |
A closer look at the middle slabs from the two raw profiles is displayed in figure 14. The middle slab shown in figure 14 is the profile of interest. Notice the differences between the two raw profiles. The CFUNs+BFUNs, as computed by the developed Hilbert-Huang-based algorithm, for the two different profiles are compared in figure 15. The two raw profiles displayed in figure 14 are not nearly as similar as the two CFUNs+BFUNs profiles shown in figure 15. Once the NFUNs were removed, the CFUNs+BFUNs for the two slab profiles closely resemble one another. These slabs were collected approximately 20 months apart, during different seasons, and the CFUNs+BFUNs profiles remain basically the same. This is likely due to the early-age built-in curl within the slabs. The developed algorithm allows for this determination.
An 11-slab section using the surface profile data from the Utah test section was also analyzed using the automated Hilbert-Huang-based profile analysis algorithm. This data is from section 493011, collected on October 9, 2007, at 3:01 p.m., during run 1, from the left wheel path. The section contains 10-inch-thick concrete of varying slab lengths.
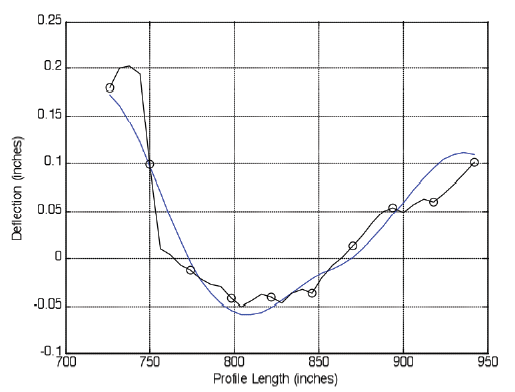
The same procedure used for the Wisconsin and Arizona LTPP test sections is applied to the Utah profile shown in figure 16. The slab profile used for analysis is centered on x ≈ 828 inches.
Again, the developed Hilbert-Huang based profile analysis algorithm successfully extracted the CFUNs+BFUNs from the middle slab profile as shown in figure 17.
Figure 14. Raw middle three Arizona LTPP 040215 slab profiles from 2010 and 2008.
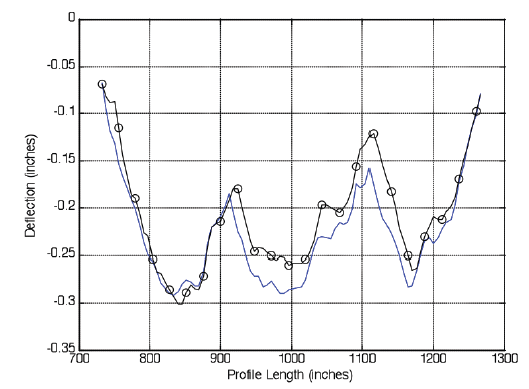 |
| ©Dan Franta |
Figure 15. CFUNs+BFUNs for the middle slabs collected in 2010 and 2008.
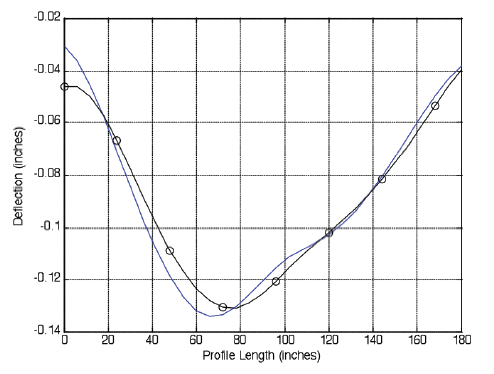 |
| ©Dan Franta |
Figure 16. Eleven-slab LTPP 493011 profile from Utah.
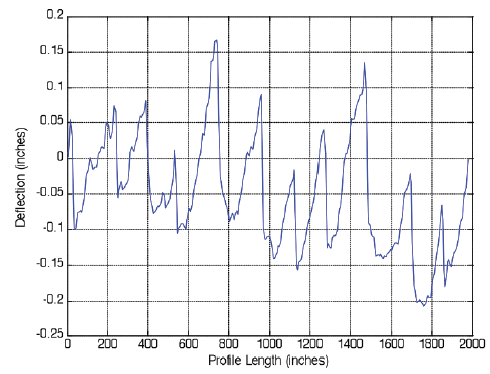 |
| ©Dan Franta |
Figure 17. Original slab profile with the CFUNs+BFUNs from the middle Utah LTPP 493011 slab profile.
 |
| ©Dan Franta |
The LTPP database contains vast amounts of surface profile data mainly used for computing IRI. The developed Hilbert-Huangbased pavement profile analysis algorithm can be used to successfully separate LTPP surface profiles into "noise/surface texture," "curl," and "base trend" sources. Trends from surface profiles were identified in Wisconsin, Arizona, and Utah LTPP profiles.
Due to spiking during sifting, it is best to discard the slabs near the edges for the multi-slab scenarios and also to neglect them during IMF grouping classifications. The length and number of slabs required for a multi-slab profile to be effectively decomposed and grouped varies with the unique characteristics of each profile. Multiple slab configurations tend to provide better separation of NFUNs, CFUNs, and BFUNs than single slab configurations and should be used with this developed profile analysis algorithm whenever possible.
The separation of the profiles allows for built-in curl analysis from LTPP surface profile data. An Arizona LTPP slab profile was shown to contain consistent "curl" deflections for the same slab over a 20-month timespan and during both winter and early fall seasons. The raw profiles were smoothed using the developed algorithm, which allowed for the analysis. The consistent slab shape is likely due to early age built-in curl.
The LTPP database is composed of multiple types of road profile sections with various slab lengths, thicknesses, and load transfer mechanisms, among other things. The developed Hilbert-Huang-based profile analysis algorithm has been proven to be universal and can be applied to any of these various road surface profiles.
A special thank you goes out to those who assisted in the funding and development of this project. I would like to acknowledge the financial support provided through the FHWA/Minnesota Department of Transportation (MnDOT) project, Determination of the Effective Built-In Curling of Concrete Pavements. From the Federal Highway Administration, I would like to thank Tom Yu. From MnDOT, I would like to thank a host of people, including Maureen Jensen, Bernard Izevbekhai, Steve Olson, Bob Strommen, Tom Burnham, Ally Akkari, and Tim Nelson.
Franta, D.P. (2012) Computational Analysis of Rigid Pavement Profiles, Master's Thesis, University Of Minnesota, Twin Cities, Minneapolis/St. Paul, MN.
"Long-Term Pavement Performance" (2011). Standard Data Release 25.0 (DVD Version), U.S. Department of Transportation, Federal Highway Administration, Washington, DC
Byrum, C. (2000). "Analysis by High-Speed Profile of Jointed Concrete Pavement Slab Curvatures." Transportation Research Record 1730, pp. 1–9, Transportation Research Board, Washington, DC.
Adu-Gyamfi, Y.O., Attoh-Okine, N.O., and Ayenu-Prah, A.Y. (2010). "Critical Analysis of Different Hilbert-Huang Algorithms for Pavement Profile Evaluation." Journal of Computing in Civil Engineering, Vol. 24, No. 6.
Attoh-Okine, N.O., Ayenu-Prah, A.Y. Jr., and Mensah, S.A. (2006). "Application of the Empirical Mode Decomposition to Pavement Profile Analysis." Department of Civil and Environmental Engineering, University of Delaware, Newark, DE.
Huang, N.E. (2005). "Introduction to the Hilbert-Huang Transform and its Related Mathematical Problems." World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ.
|
Researchers — Franta, Daniel P., Wojtkiewicz, Steven F., Khazanovich, Lev. Distribution — This report is being distributed according to a standard distribution. Direct distribution is being made to the Divisions and Resource Center. Availability —This report may be obtained from FHWA Product Distribution Center by e-mail to report.center@dot.gov, fax to (814) 239-2156, phone to (814) 239-1160, or online at https://www.fhwa.dot.gov/research/. Key Words— Built-in curl, LTPP, Hilbert-Huang, empirical mode decomposition, intrinsic mode function. Notice —This document is disseminated under the sponsorship of the U.S. Department of Transportation in the interest of information exchange. The U.S. Government assumes no liability for the use of the information contained in this document. The U.S. Government does not endorse products or manufacturers. Trademarks or manufacturers' names appear in this report only becausethey are considered essential to the objective of the document. Quality Assurance Statement —The Federal Highway Administration (FHWA) provides high-quality information to serve the Government, industry, and public in a manner that promotes public understanding. Standards and policies are used to ensure and maximize the quality, objectivity, utility, and integrity of its information. FHWA periodically reviews quality issues and adjusts its programs and processes to ensure continuous quality improvement. |