U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
 |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
Publication Number: FHWA-RD-98-085 |
From the public's perspective, the most important basic purpose of a roadway pavement is to provide a smooth safe ride. For a pavement to accomplish this purpose it must be durable, and it is the responsibility of pavement engineers to ensure that pavements are designed and constructed in such a way that they achieve this durability. Pavement researchers are continually looking for ways that will allow engineers to design and construct pavements that provide a smooth safe ride for the longest amount of time and for the least cost.
Pavements historically have been constructed from a combination of locally available natural materials, including natural soils, select soils such as natural gravel, and processed material such as quarried stone. Pavements are constructed in layers with the weaker or least durable materials at the bottom and the stronger or most durable materials at the top. The top layers are normally bound together with some sort of binder. Commonly used binders include hydraulic cements and bituminous cements. The most widely used of the bituminous cements is asphalt, a petroleum product refined from crude oil. What makes asphalt desirable for pavement construction is its tendency to stick to the granular material used in the upper pavement layers and thus to keep this material in place. In addition, when asphalt is heated, it becomes very fluid and can be mixed with gravel or rock, making it an easy material to process in the mass quantities required for pavement construction.
If a layer of asphalt bound gravel or rock is thick enough, it takes on structural characteristics of its own and contributes to the overall durability of the pavement. Pavement engineers and researchers discovered long ago that the durability of a pavement is dependent on how it is used. Heavy wheel loads, many wheel loads, or a combination of both will shorten the service life of a pavement. Thicker pavement layers were found to counteract the effects of heavier or more numerous wheel loads. Pavement researchers developed mathematical relationships to calculate the thickness required for specific accumulations of expected wheel loads. Recently developed relationships tend to relate to the specific mechanical properties of the materials used in pavement construction and to how much strain these materials can tolerate while remaining intact.
Asphalt has some unique properties that relate to the mechanical properties of an asphalt bound layer of gravel or rock. Asphalt is a liquid, albeit a very stiff liquid under normal ambient temperatures. When an asphalt material is deformed slightly, and for a very short period of time, it tends to return to its original shape. If the deformation is larger or if it occurs over a longer period of time, the asphalt does not fully return to its original shape. The amount of force needed to deform asphalt increases when the asphalt is cooled and decreases when it is warmed. In short, we have a material that deforms if loaded excessively or for too long, and how much or how long it takes to deform depends on its temperature. Another property of asphalt is that, although it is a liquid, it can crack if loaded too much, too quickly or too many times. Additionally, it may lose its bond to the gravel or rock under the same circumstances. All of these factors make asphalt a difficult material to model.
One of the mechanical properties of a blend of asphalt and gravel is its modulus, or stiffness. The particular modulus that pavement engineers are most interested in is the amount of recoverable deformation that occurs due to a load. This is sometimes termed the resilient modulus. Another property is the amount of un-recovered (plastic) deformation due to that same load. A special case of the resilient modulus is the dynamic modulus, a measure of the deformation due to an applied load, plus a measure of the time delay between load application and deformation. Asphalt also does not deform simultaneously to a load being applied, an effect known as hysteresis. Rather, it begins to deform when the load is applied and continues to deform over some period of time, although usually a fairly short amount of time. All of these stiffness properties of asphalt are very dependent on temperature. The stiffness of the asphalt layer in turn controls the amount of bending, or deflection, that will occur in a pavement when a load is applied.
There are two types of deflections that are relevant to pavement analysis:
A pavement engineer or researcher, will measure the deflection with an FWD, analyze the deflection data, usually by backcalculation, to determine a resilient modulus for the asphaltic bound layers, and then use this result to predict how much deflection a truck axle load will generate. The temperature of the asphalt must be taken into account in both cases so that deflections or modulus can be adjusted as needed.
With the trend toward mechanistic-empirical design methods, methods to adjust the pavement response for temperature are needed. One such method was developed from the Long Term Pavement Performance (LTPP) program. Within LTPP, the seasonal monitoring program (SMP) was initiated to measure pavement deflections and corresponding pavement temperatures on over 40 pavement test sections throughout the United States and Canada. The testing is conducted on half of the sections for one year, then on the other half the following year. The sections are also instrumented to measure in-pavement temperatures and moisture contents. The FWD tests were conducted at two-year intervals at the same positions within the test sections to minimize the spatial effects (variation in test results that are due to variation in the pavement in both longitudinal and transverse directions). The SMP provides the largest dataset of deflections and related pavement temperatures currently available to researchers.
To illustrate the effect that pavement temperatures have on deflections, Figure 1 and Figure 2 show the variation in deflection response to in-pavement temperatures measured at test site locations in Nebraska and Colorado. Figure 1 shows the change that occurs over the course of a few hours at the same point within the same day. Notice that the temperatures effect the deflections close to the load and not away from the load. This is because the top asphalt layer is sensitive to temperature and the underlying unbound materials such the aggregate base and subgrade soil are not. It may be argued that deflections furthest away from the load plate do not change because temperatures do not vary as much, or as quickly in those lower layers, but it is known from independent measurements that those materials are not temperature sensitive. Note that the graph shows a symmetric deflection basin for illustration purposes only. The measurements were only made at the right side of the ordinate. If deflection sensors had been placed on both sides of the load plate, the basin would have been shown to be asymmetric because pavements are not exactly uniform in all directions.
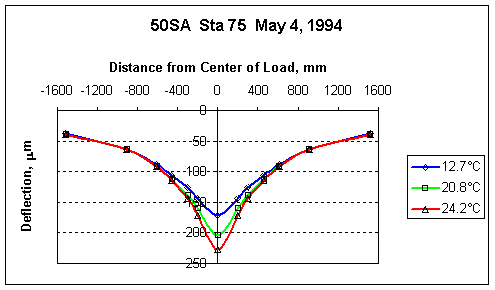
Figure 1. Variations in Deflection due to Temperature in Nebraska
Figure 2 shows the variation in deflections at a single spot on a test site in Colorado over the course of a year. The deflection is plotted against the temperature measured at the mid-depth of the asphalt pavement. Although this shows a strong relationship between temperature and deflection, other seasonal effects are reflected in this plot also. It can be seen that temperature alone explains 88 percent of the variation in the deflections. The remaining 12 percent of the variation is due to seasonal effects and random error. The seasonal effects at other locations or other pavements will be similar.
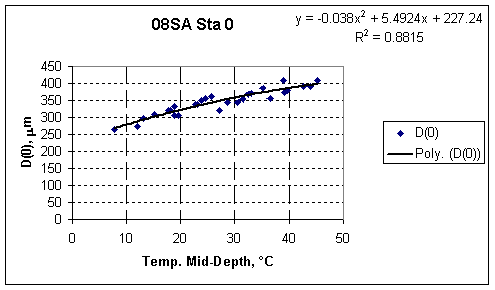
Figure 2. Variations in Deflection due to Temperature at One Location in Colorado
Figure 3 shows the combined effect of temperature and season at a location on a Nebraska test site. The deflections now show that only the outer sensor measurement remained unchanged, indicating that the seasonal effect was not evident in that sensor but did show up at the intermediate sensors. It is still evident that temperature was responsible for most of the observed changes in deflection.
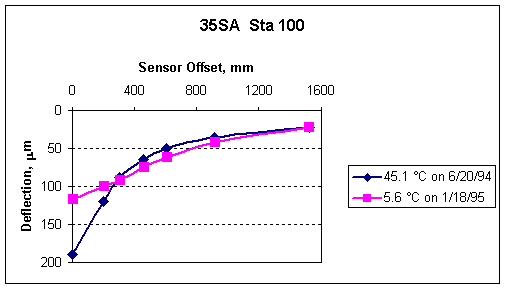
Figure 3. Temperature and Seasonal Effects in Nebraska
Figure 4 shows the backcalculated moduli for the 160 mm asphalt layer at the same location shown in Figure 3. The trend-line shows that temperature changes explain nearly 98 percent of the variation in the backcalculated moduli. The backcalculated moduli are from 18 different measurements taken from this specific point over the course of a year. If the asphalt moduli are converted to logarithms and plotted against the temperature, the plot becomes linear as shown in Figure 5.
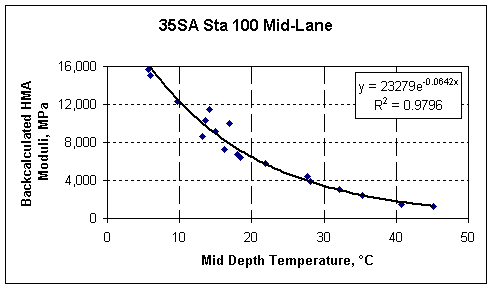
Figure 4. Variation in Backcalculated Moduli at a Location in Nebraska
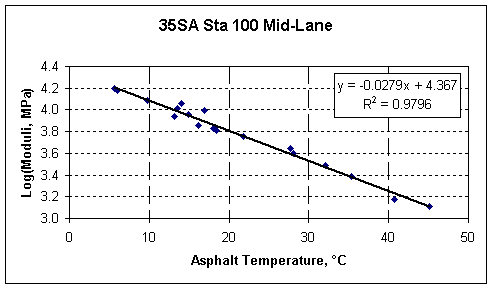
Figure 5. Variation in the Log of the Backcalculated Moduli at a Location in Nebraska
Temperature Predictions and Deflection Adjustments
The SMP, described in the previous section, provided a large amount of data that was used by Lukanen, Stubstad, and Briggs1 to develop empirical regression models for predicting in-depth pavement temperatures from surface temperatures, the time of day when the surface temperature measurement was made, and the average air temperature of the day before. With the same data, Lukanen et al developed empirical regression models that related measured deflections, deflection basin shape factors, or backcalculated moduli to the temperature of the asphalt at mid-depth. These models may be used to adjust measured deflections, deflection basin factors, or backcalculated moduli to those values expected at different temperatures.
The BELLS model is used to increase productivity and (arguably) accuracy during testing in the field. An FWD equipped with infrared (IR) sensors records surface temperatures at every test location, accounting for the effects of varying shade levels and color over the pavement surface. Temperature measurements taken in-depth at a fixed location on the test site cannot account for such variations. The surface temperatures can be input into the appropriate BELLS model to calculate the in-depth temperature for each test.
Once the in-depth temperatures are calculated, the deflections, basin shape factor, or backcalculated modulus at any other temperature can be predicted by using the models developed and presented within the Lukanen et al report.
The ability to measure deflections under any temperature and then adjust the results for all other temperatures greatly increases the usefulness of deflection testing. Without this ability, deflection test productivity would be extremely limited since it would always have to be performed at the specific pavement temperature of interest.
Evaluation of the structural capacity of an asphalt pavement typically involves the measurement of pavement deflections under a load with an FWD. At the same time that the deflections are measured, the temperature of the asphalt surface is commonly measured with an IR thermometer mounted on the FWD. If the FWD does not have such a thermometer, surface temperatures can be measured manually with a hand held instrument, or with a surface contact thermometer. Alternatively, a small hole may be drilled to allow measurement of the asphalt temperature at the desired depth directly. The procedure described here deals with using surface temperature measurements to estimate the temperature at some depth within the asphalt using the BELLS equations.
Once the temperature at depth is estimated, the deflection measurements, or the backcalculated asphalt moduli can be adjusted to the deflection or moduli expected at any other temperature. Detailed descriptions of using BELLS to estimate mid-depth temperatures and to adjust deflection responses for the effects of temperature follow.
Reference