LTPP Guide to Asphalt Temperature Prediction and Correction

Two BELLS models are presented by Lukanen et al. One is for use with LTPP protocol testing and the other for routine testing. The difference between the two is that the LTPP testing model accounts for the time it takes to conduct each FWD test and move forward to the next test location. During this period, the pavement surface where the temperature is measured with the FWD’s IR sensor has been shaded for five to six minutes. The shading allows the surface to cool, particularly on sunny days. Even on cloudy days, there is some measure of surface heating from solar radiation. The LTPP data used to develop the BELLS model was collected under such shading conditions. FWD tests conducted routinely by most highway agencies typically require the equipment to be on a specific test location for a minute or less, resulting in much less cooling of the pavement surface. To adjust for cooling, the LTPP surface temperature data was adjusted upward by different amounts, depending on the amount of cloud cover. This "shade adjusted" data was used to develop another BELLS model that is more suited for routine testing. The basic model and the "shade-adjusted" model are referred to in the report as BELLS2 and BELLS3 respectively.

Utilization of the appropriate BELLS model allows a pavement engineer to calculate the temperature within an asphalt pavement at each test location if an IR sensor was mounted on the FWD. Even without such a sensor, manually measured surface temperatures can be obtained quickly, eliminating the time-consuming process of drilling holes in the pavement, allowing the heat of drilling to dissipate, and then measuring the temperature at the bottom of the hole. As indicated above, frequent measurements might provide better in-depth temperature results overall than would be possible using the less frequent manual measurements made in drilled holes.

Four data items are needed to calculate a temperature at depth using BELLS:

• Surface Temperature in degrees Celsius.
• Time of day (24 hour clock).
• Distance below the surface where the temperature is to be calculated in millimeters.
• Average air temperature of the previous day in degrees Celsius.

Temperature calculations for LTPP testing where the tow vehicle and FWD trailer shade the pavement for more than three minutes is based on the following equation:

BELLS2 (LTPP testing Protocol)

T_d = 2.78 + 0.912 * IR + {log(d) - 1.25}{-0.428 * IR + 0.553 * (1-day) + 2.63 * sin(hr₁₈ - 15.5)} + 0.027 * IR* sin(hr₁₈ - 13.5)

Where:

T_d = Pavement temperature at depth d, °C

IR = Pavement surface temperature, °C

log = Base 10 logarithm

d = Depth at which material temperature is to be predicted, mm

1-day = Average air temperature the day before testing, °C

sin = sine function on an 18-hr clock system, with 2π radians equal to one 18-hr cycle

hr₁₈ = Time of day, in a 24-hr clock system, but calculated using an 18-hr asphalt concrete (AC) temperature rise-and-fall time cycle, as indicated in Figure 6

Source code for implementing this equation as a function in MS Excel VBA is available here.

Sample data for checking code is available here.

Routine testing that shades the pavement surface for closer to 30 seconds is based on the following equation:

BELLS3 (Routine testing methods)

T_d = 0.95 + 0.892 * IR + {log(d) - 1.25}{-0.448 * IR + 0.621 * (1-day) + 1.83 * sin(hr₁₈ - 15.5)} + 0.042 * IR * sin(hr₁₈ - 13.5)

Where:

T_d = Pavement temperature at depth d, °C

IR = Pavement surface temperature, °C

log = Base 10 logarithm

d = Depth at which mat temperature is to be predicted, mm

1-day = Average air temperature the day before testing, °C

sin = Sine function on an 18-hr clock system, with 2π radians equal to one 18-hr cycle

hr₁₈ = Time of day, in a 24-hr clock system, but calculated using an 18-hr asphalt concrete (AC) temperature rise-and-fall time cycle, as indicated in Figure 6

Source code for implementing this equation as a function in MS Excel VBA is available here.

Sample data for checking code is available here.

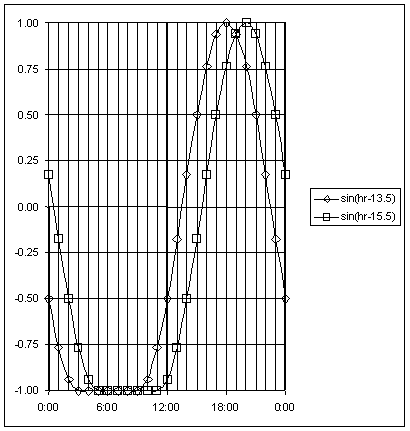
Figure 6. 18-hr Sine Function Used in BELLS Equations

Notes:

When using the sin(hr₁₈ - 15.5) (decimal) function, only use times from 11:00 to 05:00 hours. If the actual time is not within this time range, then calculate the sine as if the time was 11:00 hours (where the sine = -1). If the time is between midnight and 05:00 hourrs, add 24 to the actual (decimal) time. Then calculate as follows: If the time is 13:15, then in decimal form, 13.25 - 15.50 = -2.25; -2.25/18 = -0.125; -0.125 x 2 = -0.785 radians; sin(-0.785) = -0.707. [Note that an 18-hr sine function is assumed, with "flat" negative 1 segment between 05:00 and 11:00 hours as shown by the solid line in Figure 6.]

When using the sin(hr₁₈ - 13.5) (decimal) function, only use times from 09:00 to 03:00 hours. If the actual time is not within this time range, then calculate the sine as if the time is 09:00 hours (where the sine = -1). If the time is between midnight and 03:00 hours, add 24 to the actual (decimal) time. Then calculate as follows: If the time is 15:08, then in decimal form, 15.13 - 13.50 = 1.63; 1.63/18 = 0.091; 0.091 x 2 = 0.569 radians; sin(0.569) = 0.539. [Note that an 18-hr sine function is assumed, with "flat" negative 1 segment between 03:00 and 09:00 hours as shown by the dotted line in Figure 6.]

Previous | Table of Contents | Next