U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-14-067 Date: September 2014 |
Publication Number: FHWA-HRT-14-067 Date: September 2014 |
VIBRATION OF TAUT STRING WITH DISTRIBUTED DAMPING
The transverse vibration of a taut string with uniformly distributed viscous damping can be described by:
![]()
Figure 2. Equation. Equation of motion (EOM) for a string.
where w(x,t) = transverse displacement, m = mass density per unit length, c = viscous coefficient per unit length, and H = pretension of the string.(2) For a string of length L, fixed at both ends, w(x,t) can be approximated by a finite degrees of freedom (DOF) system:
![]()
Figure 3. Equation. General solution of EOM.
where the sinusoidal spatial functions sin(nπx/L)are the normal modes for a string where c = 0. Substituting w(x,t) into the equation in figure 2 and rearranging yields the following:
![]()
Figure 4. Equation. EOM for a string.
for n = 1, 2, ...,N (no sum on n). The equation in figure 4 represents the equation of motion for the nth mode vibration of the string, ωn and ζn, respectively, denote the corresponding circular natural frequency and damping ratio of the mode. It is to be noted that the equations for this N-DOF system are fully decoupled and each mode can be handled separately. Using the standard solution technique for a single DOF system, a general solution to the equation in figure 4 follows:
![]()
Figure 5. Equation. General solution to EOM.
where An and αn are the amplitude and phase angle that are dependent on the initial conditions of the vibration, and the following:
![]()
Figure 6. Equation. Damped natural frequency.
is the damped natural frequency.(3)
DETERMINATION OF DAMPING RATIOS
The damping ratio, or the fraction of critical damping, ζn, can be estimated experimentally. In the logarithmic decrement method, the damping ratio is found by measuring the amplitude of two consecutive peaks of damped free vibration and computing their ratio.(3) It can be shown that the ratio between the two consecutive peaks of the vibration is given by the following expression:
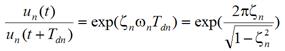
Figure 7. Equation. Ratio of two consecutive peaks.
where Tdn = 2π/ωdn is the damped natural period of the nth mode. Selecting two consecutive peaks ui and ui+1 and taking the natural logarithm of the equation in figure 7, one finds the expression for the logarithmic decrement defined by:
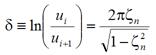
Figure 8. Equation. Logarithmic decrement.
For lightly damped systems (ζn < 0.2), the equation in figure 8 can be simplified to ![]() . This simplification is valid for inherent damping ratios of most stay cables, which are almost always below 0.01. From this simplification and the equation in figure 8, the damping ratio can be obtained by:
. This simplification is valid for inherent damping ratios of most stay cables, which are almost always below 0.01. From this simplification and the equation in figure 8, the damping ratio can be obtained by:
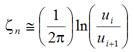
Figure 9. Equation. Damping ratio.
The equation in figure 9 is valid for both displacement and acceleration decay curves for lightly damped systems.