Measured Variability Of Southern Yellow Pine - Manual for LS-DYNA Wood Material Model 143
PDF files can be viewed with the Acrobat® Reader®
2.3 FITTING THE MODEL TO THE DATA
| 1. |
|
Stiffnesses (EL, ET, GLT, and GTR) and the major Poisson’s ratio (nLT) are directly measured from the elastic portion of the stress-strain curves or are selected from data tabulated in the literature. If the parallel stiffness EL is known, then one can estimate the other elastic stiffnesses from tables documented in the literature for softwoods (e.g., pine).(16) Typically, ET is 5 to 15 percent of EL. Care must be taken to measure or select the correct Poisson’s ratio. The major ratio, nLT, is typically greater than 0.1 and is about 10 times larger than the minor ratio, nTL.
|
| 2. |
|
Strengths (XT, XC, YT, YC, S||, and S^) are obtained from measurements of peak/yield stress from stress histories or are selected from data tabulated in the literature. Typically, the parallel tensile strength of pine is 30 to 50 times greater than the perpendicular tensile strength. The parallel compressive strength is four to five times greater than the perpendicular compressive strength. The parallel shear strength is about 10 to 15 percent of the parallel tensile strength. Data for perpendicular shear strength vary. One source suggests that the perpendicular shear strength, S^, is 140 percent of the parallel shear strength, S||.(7) Another source suggests that the percentage is only 18 to 28 percent.(18)
|
| 3. |
|
The prepeak hardening parameters (N||, c||, N^, and c^) are derived from the nonlinear portion of compressive stress-strain curves measured both parallel and perpendicular to the grain. Hardening is modeled separately for the parallel and perpendicular modes. The parameters N|| and N^ determine the onset of nonlinearity. If the user wants prepeak nonlinearity to initiate at 70 percent of the yield stress, then the user would input N = 0.3 (for 30 percent), which is derived from N = 1 – 0.7 (100 percent – 70 percent). The parameters c|| and c^ set the amount of nonlinearity and are selected through iteration: Pick a value for c, plot the results from a single-element simulation, and compare with the test data. Typical values of c are between 100 and 1000 (unitless). Gradual hardening is accomplished with smaller values of c. Rapid hardening is accomplished with larger values of c. If no data are available, prepeak hardening can be neglected (giving a linear stress-strain curve to yield) by setting both values of N equal to zero.
|
| 4. |
|
The fracture energy (Gf I ||, Gf II ||, Gf I ^, or Gf II^) is the area under the stress-displacement curve as it softens from peak stress to zero stress. The best approach is to measure fracture energy directly in both direct tension and simple shear. An alternative approach is to measure fracture intensity and convert it to fracture energy.
|
| 5. |
|
The postpeak softening parameters (B and D) are derived from the softening portion of the stress-strain or stress-displacement curves and are set in conjunction with the fracture energies (Gf I ||, Gf II ||, Gf I^, and Gf II^) and the damage parameters (dmax|| and dmax^). The parameters B (for parallel modes) and D (for perpendicular modes) set the shape of the softening portion of the stress-strain or stress-displacement curves once the fracture energy is selected. Although each parameter (B or D) is intended to be simultaneously fit to both tension and shear data, shear data are rarely available. The procedure is iterative: Pick a value for D or B, plot the results from a single-element simulation, and compare with the test data. Typical values for B and D are 10 to 50 (unitless). The smaller the value, the more gradual the initial softening.
|
| 6. |
|
The postpeak damage parameters (dmax|| and dmax^) are derived from the final softening portion of the stress-strain or stress-displacement curves and are set in conjunction with the fracture energies (Gf I ||, Gf II ||, Gf I^, and Gf II^) and the softening parameters (B and D). The parameters dmax|| (for parallel modes) and dmax^ (for perpendicular modes) set the maximum damage that can accumulate. Values between 0 and 1 are allowed. A value of 0 neglects softening, while a value of 1 models complete softening to 0 stress and stiffness. A typical value for parallel damage is dmax|| = 0.9999. Erosion is automatically modeled when parallel damage exceeds 0.99. Set dmax|| > 0.99 to model erosion at high damage levels. Set dmax|| £ 0.99 to bypass erosion (not recommended because this may cause mesh entanglement and element inversion). A typical value for perpendicular damage is dmax^ = 0.99. Values greater than 0.99 are not recommended because elements have a tendency to tangle and invert with near zero stiffness, and erosion is not automatically modeled with perpendicular damage. Values less than 0.99 should be input if mesh entanglement and element inversion are a problem.
|
| 7. |
|
The rate-effect parameters (h||, hc||, n||, h^, hc^, and n^) are obtained from fits to strength versus strain-rate measurements or are selected from data tabulated in the literature. Separate measurements must be made parallel and perpendicular to the grain to separately fit the parameters parallel (h||, hc||, and n||) and perpendicular (h^, hc^, and n^) to the grain. Separate measurements may also be made in tension/shear versus compression to separately fit the tensile/shear (h|| or h^) and compression (hc|| or hc^) parameters. If separate tension/shear versus compression measurements are not available, then the following ratios are recommended: h||/hc|| = h^/hc^ = QT / QC. Each set of parameters is obtained from dynamic strength measurements at two different strain rates (because there are two parameters), as well as from the static strength (zero strain rate). At each of two strain rates, the difference between the dynamic and static strength is C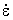 h, where C is the stiffness (EL, ET, GLT, or GTR), h, where C is the stiffness (EL, ET, GLT, or GTR), 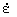 is the effective strain rate, and h is the effective fluidity parameter equal to h = h0/ is the effective strain rate, and h is the effective fluidity parameter equal to h = h0/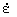 n. Here, h0 (h|| or hc||, or h^ or hc^) and n (n|| or n^) are the two parameters to be fit (C and n. Here, h0 (h|| or hc||, or h^ or hc^) and n (n|| or n^) are the two parameters to be fit (C and 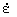 are known). The two parameters are found by simultaneously solving two equations with two unknowns (see equation 60 in the Model Formulation section). Typical clear wood values are n|| = 0.107, with h|| = hc|| = 0.0045 for parallel rate effects, and n^ = 0.104, with h^ = hc^ = 0.0962 for perpendicular rate effects (for time in milliseconds). Typical graded wood values are n|| = 0.107, with h|| = 0.0045QT and hc|| = 0.0045QC (parallel), and n^ = 0.104, with h^ = 0.0962QT and hc^ = 0.0962QC (perpendicular). are known). The two parameters are found by simultaneously solving two equations with two unknowns (see equation 60 in the Model Formulation section). Typical clear wood values are n|| = 0.107, with h|| = hc|| = 0.0045 for parallel rate effects, and n^ = 0.104, with h^ = hc^ = 0.0962 for perpendicular rate effects (for time in milliseconds). Typical graded wood values are n|| = 0.107, with h|| = 0.0045QT and hc|| = 0.0045QC (parallel), and n^ = 0.104, with h^ = 0.0962QT and hc^ = 0.0962QC (perpendicular). |
Previous | Table of Contents | Next
|
