Measured Variability Of Southern Yellow Pine - Manual for LS-DYNA Wood Material Model 143
PDF files can be viewed with the Acrobat® Reader®
Foreword
This report documents a wood material model that has been implemented into the dynamic finite element code, LS-DYNA, beginning with version 970. This material model was developed specifically to predict the dynamic performance of wood components used in roadside safety structures when undergoing a collision by a motor vehicle. This model is applicable for all varieties of wood when appropriate material coefficients are inserted. Default material coefficients for two wood varieties―southern yellow pine and Douglas fir―are stored in the model and can be accessed for use.
This report is one of two that completely documents this material model. This report, Manual for LS-DYNA Wood Material Model 143 (FHWA-HRT-04-097), completely documents this material model for the user. The companion report, Evaluation of LS-DYNA Wood Material Model 143 (FHWA-HRT-04-096), completely documents the model’s performance and the accuracy of the results. This performance evaluation was a collaboration between the model developer and the model evaluator. Regarding the model performance evaluation, the developer and the evaluator were unable to come to a final agreement regarding the model’s performance and accuracy. These disagreements are itemized and thoroughly discussed in section 17 of the second report.
This manual will be of interest to research engineers associated with the evaluation and crashworthy performance of roadside safety structures, particularly those engineers responsible for the prediction of the crash response of such structures when using the finite element code LS-DYNA.
Michael F. Trentacoste
Director
Office of Safety
Research and Development
Notice
This document is disseminated under the sponsorship of the
U.S. Department of Transportation in the interest of information exchange. The
U.S. Government assumes no liability for the use of the information contained in this document.
The
U.S. Government does not endorse products or manufacturers. Trademarks or manufacturers' names appear in this report only because they are considered essential to the objective of the document.
Quality Assurance Statement
The Federal Highway Administration (FHWA) provides high-quality information to serve Government, industry, and the public in a manner that promotes public understanding. Standards and policies are used to ensure and maximize the quality, objectivity, utility, and integrity of its information. FHWA periodically reviews quality issues and adjusts its programs and processes to ensure continuous quality improvement.
Technical Report Documentation Page
1. Report No.
FHWA-HRT-04-097 |
2. Government Accession No. |
3. Recipient's Catalog No. |
4. Title and Subtitle
MANUAL FOR LS-DYNA WOOD MATERIAL MODEL 143
|
5. Report Date
August 2007 |
6. Performing Organization Code
|
7. Author(s)
Yvonne D. Murray |
8. Performing Organization Report No. |
9. Performing Organization Name and Address
APTEK, Inc.
1257 Lake Plaza Drive
Colorado Springs, CO 80906-3558 |
10. Work Unit No. (TRAIS)
|
11. Contract or Grant No.
DTFH61-98-C-00071 |
12. Sponsoring Agency Name and Address
Office of Safety Research and Development
Federal Highway Administration
6300 Georgetown Pike
McLean, VA 22101-2296 |
13. Type of Report and Period Covered
Final Report
Sept. 28, 1998 - Sept. 13, 2002 |
14. Sponsoring Agency Code
|
15. Supplementary Notes
Contracting Officer’s Technical Representative (COTR): Martin Hargrave, HRDS-04 |
|
16. Abstract
An elastoplastic damage model with rate effects was developed for wood and was implemented into LS-DYNA, a commercially available finite element code. This manual documents the theory of the wood material model, describes the LS-DYNA input and output formats, and provides example problems for use as a learning tool. Default material property input options are provided for southern yellow pine and Douglas fir. The model was developed for roadside safety applications, such as wood guardrail posts impacted by vehicles; however, it should be applicable to most dynamic applications.
The companion report to this manual is:
Evaluation of LS-DYNA Wood Material Model 143 (FHWA-HRT-04-096)
|
17. Key Words
Wood, LS-DYNA, orthotropic, material model, damage, rate effects,guardrail |
18. Distribution Statement
No restrictions. This document is available to the public through the National Technical Information Service, Springfield, VA 22161. |
19. Security Classif. (of this report)
Unclassified |
20. Security Classif. (of this page)
Unclassified |
21. No. of Pages
163 |
22. Price
|
| Form DOT F 1700.7 (8-72) |
Reproduction of completed page authorized. |
Preface
|
|
The goal of the work performed under this program, Development of DYNA3D Analysis Tools for Roadside Safety Applications, is to develop wood and soil material models, implement the models into the LS-DYNA finite element code, and evaluate the performance of each model through correlations with available test data.(1)
This work was performed under Federal Highway Administration (FHWA) Contract No. DTFH61-98-C-00071. The FHWA Contracting Officer's Technical Representative (COTR) was Martin Hargrave.
Two reports are available for each material model. One report is a user's manual; the second report is a performance evaluation. This user's manual, Manual for LS-DYNA Wood Material Model 143, thoroughly documents the wood model theory; reviews the model input; and provides example problems for use as a learning tool. It is written by the developer of the model. The performance evaluation for the wood model, Evaluation of LS-DYNA Wood Material Model 143, documents LS DYNA parametric studies and correlations with test data performed by the model developer and by a potential end user.(2) The reader is urged to review this user's manual before reading the evaluation report. A user's manual and evaluation report are also available for the soil model.(3,4)
The development of the wood model was conducted by the prime contractor. The associated wood model evaluation effort to determine the model's performance and the accuracy of the results was a collaboration between two contractors, with each evaluation intended to be independent of the other. The prime contractor developed and partially evaluated the wood model. The subcontractor performed a second independent evaluation of the wood model, provided finite element meshes for the evaluation calculations, and provided static post and bogie impact test data for correlations with the model. Others provided valuable material property data for clear wood pine, and static compression and bending test data for correlations. A final company implemented the wood model into the LS-DYNA finite element code.
The developer and the evaluator were unable to come to a final agreement regarding several issues associated with the model's performance and accuracy during the second independent evaluation of the wood model. These issues are itemized and thoroughly discussed in section 17 of the wood model evaluation report.(2)
|
Table of Contents
Appendix A. Measured Variability of Southern Yellow Pine
Appendix B. Quadratic Equations Fit to Moisture Content Data
Appendix C. Analytical Form of Candidate Failure Criteria
Appendix D. Graphical Comparison of Candidate Failure Criteria
Appendix E. Derivation of Consistency Parameter for Plasticity Algorithm
Appendix F. Derivation of Limiting Function for Hardening Model
Appendix G. Single-Element Input File
References
List of Figures
Figure 1. Wood material properties vary with orientation. The wood material coordinate system does not necessarily coincide with the board coordinate system. Source: American Society of Civil Engineers
Figure 2. Ultimate tensile strength of Douglas fir measured in off-axis tests drops rapidly as the load is oriented at increasing angles to the grain. Source: Society of Wood Science and Technology
Figure 3. Measured stress-strain relationships of southern yellow pine depend on load direction (parallel or perpendicular), load type (tensile or compressive), and moisture content
Figure 4. Temperature affects the dynamic behavior of wood posts impacted by bogies at 9.4 m/s.
Figure 5. Wood exhibits progressive softening. Source: Forest Products Laboratory
Figure 6. Wood exhibits modulus reduction and permanent deformation (splitting test data for spruce wood from Stanzi-Tschegg, et al.). Source: Kluwer Academic Publishers, with the permission of Springer Science and Business Media
Figure 7. Variability of southern yellow pine clear wood data at 12-percent moisture content depends on load direction and type
Figure 8. Wood material properties vary with position. Board strength depends on position and size of knot. Source: Society of Wood Science and Technology
Figure 9. Dynamic strength of wood increases with impact velocity in Hopkinson bar tests and is most pronounced in the perpendicular direction. Source: Pergamon, Elsevier Science Ltd
Figure 10. Organization of wood material model
Figure 11. Failure criteria for wood depend on four of the five invariants of a transversely isotropic material
Figure 12. Failure criteria for wood produce smooth surfaces in stress space
Figure 13. Prepeak nonlinearity is modeled in compression with translating yield surfaces that allow user to specify the hardening response
Figure 14. Postpeak hardening is modeled in compression with positive values of the parameter Ghard
Figure 15. Damage d accumulates with energy t once an initial threshold t0 is exceeded
Figure 16. Softening depends on the values of the damage parameters C and D (calculated with dmax = 1)
Figure 17. Softening response modeled for parallel modes of southern yellow pine
Figure 18. Softening response modeled for perpendicular modes of southern yellow pine
Figure 19. Hopkinson bar tests indicate that the measured strength of pine increases with impact velocity. Source: Pergamon, Elsevier Science Ltd.(11)
Figure 20. Hopkinson bar data indicate that strength and stiffness increase with strain rate. Source: EDP Sciences
Figure 21. These single-element simulations demonstrate the rate-effect behavior of the shifted surface formulation at 500/s
Figure 22. Two-parameter viscoplastic model is flexible in fitting data
Figure 23. These single-element simulations demonstrate the rate-effect behavior of the viscoplastic formulation at 500/s
Figure 24. Effect of temperature and moisture interaction on longitudinal modulus
Figure 25. Temperature effects are more pronounced for the strength parallel to the grain than for the modulus parallel to the grain. Source: Forest Products Laboratory
Figure 26. Yield criteria for wood produce smooth surfaces in stress space
Figure 27. Prepeak nonlinearity in compression is modeled with translating yield surfaces that allow user to specify hardening response
Figure 28. Softening response modeled for parallel modes of southern yellow pine
Figure 29. Example wood model input for selection of default input parameter (option MAT_WOOD_PINE)
Figure 30. Example wood model input for user specification of input parameters (option MAT_WOOD)
Figure 31. Example single-element stress-strain results for clear wood pine
Figure 32. Deformed configuration of post at 40 ms, including fringes of damage
Figure 33. Post deflection and cross-sectional force histories
Figure 34. Measured load displacement curves of southern yellow pine exhibit variability in tension parallel to the grain. Source: Forest Products Laboratory(14)
Figure 35. Measured load displacement curves of southern yellow pine exhibit variability in compression perpendicular to the grain. Source: Forest Products Laboratory
Figure 36. Effect of moisture content on tensile modulus parallel to the grain. Source: Forest Products Laboratory
Figure 37. Effect of moisture content on tensile modulus perpendicular to the grain. Source: Forest Products Laboratory
Figure 38. Effect of moisture content on tensile strength parallel to the grain. Source: Forest Products Laboratory.(14)
Figure 39. Effect of moisture content on tensile strength perpendicular to the grain. Source: Forest Products Laboratory.(14)
Figure 40. Effect of moisture content on compressive strength parallel to the grain. Source: Forest Products Laboratory.(14)
Figure 41. Effect of moisture content on compressive strength perpendicular to the grain. Source: Forest Products Laboratory.(14)
Figure 42. Effect of moisture content on shear strength parallel to the grain. Source: Forest Products Laboratory.(14)
Figure 43. Effect of moisture content on mode I fracture intensity. Source: Forest Products Laboratory
Figure 44. Effect of moisture content on mode II fracture intensity. Source: Forest Products Laboratory
Figure 45. Compressive strength variation of clear wood is readily modeled by a sinusoidal correction in the R-T plane. Source: Krieger Publishing Company.(16)
Figure 46. Geometry of an off-axis test specimen. Source: Krieger Publishing Company.(16)
Figure 47. Most of the interactive failure criteria are in agreement with Hankinson’s formula for the off-axis strength of southern yellow pine in the L-T plane
Figure 48. Effect of ring angle variation at 90-degree grain angle on the relative compression strength of four wood species. Source: Society of Wood Science and Technology
Figure 49. Failure criteria comparison for perpendicular modes as a function of the ring angle
Figure 50. Predicted effect of perpendicular confinement and extension on the longitudinal strength of southern yellow pine in tension and compression
Figure 51. Predicted effect of parallel shear and tangential stresses on the longitudinal strength of southern yellow pine in tension and compression
Figure 52. Predicted effect of parallel shear invariant on the longitudinal strength of southern yellow pine in tension and compression
Figure 53. Predicted strength of southern yellow pine perpendicular to the grain (no perpendicular shear stress applied)
Figure 54. Shape of the failure surface is sensitive to perpendicular shear strength if the criteria are transversely isotropic
Figure 55. Combinations of perpendicular and shear stresses that satisfy the failure criteria in the isotropic plane
Figure 56. Single-element input file
Figure 57. First continuation of single-element input file
Figure 58. Second continuation of single-element input file
List of Tables
Table 1. Average elastic moduli of southern yellow pine
Table 2. Average elastic moduli of Douglas fir
Table 3. LS-DYNA default values for the room-temperature moduli (graded or clear wood) of southern yellow pine and Douglas fir at saturation
Table 4. Average strength data for southern yellow pine
Table 5. Average strength data for Douglas fir
Table 6. LS-DYNA default values for room-temperature clear wood strengths of southern yellow pine and Douglas fir at fiber saturation.*
Table 7. Default hardening parameters for clear wood southern yellow pine and Douglas fir
Table 8. LS-DYNA default values for room-temperature clear wood softening parameters for southern yellow pine and Douglas fir at saturation
Table 9. Average fracture intensity data for southern yellow pine measured perpendicular to the grain
Table 10. Room-temperature clear wood fracture energies for southern yellow pine and Douglas fir as a function of moisture content (derived from measured fracture intensities)
Table 11. Strength ratios versus strain rate derived from compressive rate-effect data
Table 12. Default LS-DYNA rate-effect parameters that provide the dynamic-to-static compressive strength ratios listed in table 11 (based on units of milliseconds for time) for pine at 12-percent moisture content
Table 13. User-supplied parameters for wood material model
Table 14. Default material property requests for wood material model
Table 15. Equations fit to moisture content data for southern yellow pine
Table 16. Equations fit to stiffness moisture content data for Douglas fir
Table 17. Input options for modeling strength reductions by grade
| Symbols |
| B, D |
Softening parameters (parallel and perpendicular)
|
| CI, CII |
Constants that relate fracture intensity to fracture energy
|
| Cijkl |
Material stiffness tensor (elastic moduli)
|
| Cij |
Material stiffness components
|
| c||, c^ |
Hardening-rate parameters (parallel and perpendicular)
|
| d, d||, d^, dm |
Scalar damage parameters (general, parallel, perpendicular, and max(d||, d^))
|
| dmax||, dmax^ |
Maximum damage allowed (parallel and perpendicular)
|
| E11, E22, E33 |
Normal moduli of an orthotropic material
|
| EL, ET |
Normal moduli (wood notation)
|
| FM, FS |
Factors to scale moduli and strengths with temperature
|
| f||, f^ |
Yield surface functions (parallel and perpendicular)
|
| f||*, f^* |
Trial elastic yield surface functions (parallel and perpendicular)
|
| G||, G^ |
Hardening model translational limit functions (parallel and perpendicular)
|
| Gf ||, Gf ^ |
Fracture energies (tension and shear)
|
| Gf I ||, Gf II || |
Parallel fracture energies (tension and shear)
|
| Gf I ^, Gf II ^ |
Perpendicular fracture energies (tension and shear)
|
| Ghard |
Hardening parameter to override perfect plasticity
|
| G12, G13, G23 |
Shear moduli of an orthotropic material
|
| GLT, GLR, GTR |
Shear moduli (wood notation)
|
| I1, I2, I3, I4 |
Stress invariants of a transversely isotropic material
|
| I1*, I2*, I3*, I4* |
Trial elastic stress invariants
|
| KI, KII |
Fracture intensities (tension and shear)
|
| L |
Element length
|
| MC |
Moisture content
|
| n||, n^ |
Rate-effect power parameters (parallel and perpendicular)
|
| N||, N^ |
Hardening initiation parameters (parallel and perpendicular)
|
| QT, QC |
Quality factors (tension/shear and compression)
|
| Â |
Stress enhancement factors (ratio of dynamic to static strength)
|
| Sij |
Compliance coefficients (reciprocals of elastic moduli)
|
| S||, S^ |
Shear strengths (parallel and perpendicular)
|
| T |
Temperature
|
| V |
Impact velocity in Hopkinson pressure bar tests
|
| X, XT, XC |
Parallel wood strengths (general, tension, and compression)
|
| Y, YT, YC |
Perpendicular wood strengths (general, tension, and compression)
|
| aij |
Backstress tensor (and incremental backstress for hardening model
|
| g, g||, g^ |
Viscoplastic interpolation parameters (general, parallel, and perpendicular)
|
| eij, Deij |
Strain tensor and strain increments
|
| e11, e22, e33, e12, e13, e23 |
Strain components of an orthotropic material
|
| e1, e2, e3, e4, e5, e6 |
Strain components (shorthand notation)
|
| eL, eT, eR, eLT, eLR, eTR |
Strain components (wood notation)
|
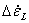 , , 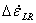 , , 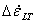 |
Strain-rate increments parallel to the grain (wood notation)
|
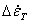 , , 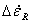 , , 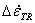 |
Strain-rate increments perpendicular to the grain (wood notation)
|
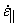 , , 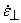 |
Scalar effective strain rates (parallel and perpendicular)
|
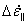 , , 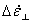 |
Scalar effective strain-rate increments (parallel and perpendicular)
|
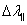 , , 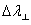 |
Plasticity consistency parameters (parallel and perpendicular)
|
| Dt |
Time-step increment
|
| h |
General rate-effect fluidity parameter
|
| h||, h^ |
Tension/shear rate-effect fluidity parameters (parallel and perpendicular)
|
| hc||, hc^ |
Compression rate-effect fluidity parameters (parallel and perpendicular)
|
| r, rs |
Density of wood and of wood solid phase
|
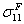 , , 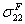 |
Ultimate yield surfaces (parallel and perpendicular)
|
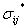 , , 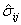 , , 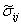 , , 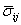 , , 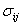 |
Stress tensors (trial elastic, inviscid, inviscid with backstress, viscid, and viscid with damage)
|
| s11, s22, s33, s12, s13, s23 |
Stress components of an orthotropic material
|
| s1, s2, s3, s4, s5, s6 |
Stress components (shorthand notation)
|
| sL, sT, sR, sLT, sLR, sTR |
Stress components (wood notation)
|
| t||, t^ |
Instantaneous strain energy type term for damage accumulation
|
| t0||, t0^ |
Initial strain energy type value for damage initiation
|
| nij |
Poisson’s ratios (indicial notation)
|
| nLT, nLR, nTR |
Major Poisson’s ratios (wood notation)
|
| Subscripts |
| L |
Longitudinal or parallel
|
| T |
Transverse or perpendicular
|
| R |
Radial
|
| || |
Parallel
|
| ^ |
Perpendicular
|
Table of Contents | Next
|
