U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-14-020 Date: January 2015 |
Publication Number: FHWA-HRT-14-020 Date: January 2015 |
A crash analysis was conducted in addition to the speed analyses. Crash data were collected for up to 4 years before and up to 3 years after sign installation. To select treatment and control sites, crash data for 3 years before installation of the signs and for all sites except Iowa were requested from the corresponding State or county agency as described in chapter 2.
The team had access to the Iowa crash database and was able to extract all the necessary crash variables for Iowa. Once the signs had been installed for at least 2 years in other States, the team contacted the corresponding State or county agency again and requested crash data for the intervening period from the original data request before sign installation. In some cases, more than 2 years had elapsed, and the agency provided more than 2 years of data.
Several models were developed that included different types of crashes. In all cases, quarterly crash frequency was the response variable used. Data were aggregated to quarters rather than years since given a limited amount of after periods were available, and use of quarters allowed the quarter in which installation occurred to be excluded from the analysis without having to exclude the entire installation year. In addition, the signs were not functioning at several sites for various periods, so the quarter in which the signs were nonfunctional could also be excluded from the analysis. Year and quarter when a crash occurred were derived from the date of crash.
Use of quarters also allowed season to be included as a covariate. A relationship between crashes and season is expected, given more crashes may occur during winter or regular wet weather conditions. More crashes may also occur in the summer months when more driving occurs. Quarters were designated using the following convention, which aggregates months during which weather conditions were the most likely to be similar:
In addition, use of season as a covariate allowed the team to account for differences that may have occurred due to an unequal distribution of quarters in the before and after period.
The following four different models were developed:
Crashes for vehicles traveling in the direction of the DSFS sign were evaluated separately because the sign was most likely to reduce crashes for vehicles traveling in that direction. A model was also developed for crashes in both directions (total crashes) because slowing vehicles in one direction may have some impact on vehicles in the opposite direction.
When aggregated by direction, crashes for single vehicles traveling in the indicated direction and multivehicle crashes where one or more vehicles were traveling in the indicated direction were included. At treatment sites, the direction included was the direction of the sign (i.e., WB). The signs were installed to face the direction where most crashes had occurred based on preliminary crash data. In all cases, this was in the direction of the outside of the curve. Given the primary direction for treatment sites was the outside of the curve, crashes in the direction of the outside curve were aggregated by quarter for control sites as well.
An attempt was made to develop a model for fatal crashes. However, the number of fatal crashes per site was low, and there were not sufficient data to develop a reliable model.
AADT was used as a measure of exposure. Given the study period was fairly short term, in most cases, AADT was the same or similar for the before and after periods. When possible, the team requested data for only the curve of interest (treatment or control). However, different States geolocate crashes differently, so in some cases, the agency provided crashes for a section that may have included adjacent curves and some tangent sections. To account for differences in curve and section length, section length was also modeled as a covariate.
Table 47 describes the covariates included in the models. Originally, the team intended to include a number of factors in the crash analysis, such as whether the crash had been designated as speed related, time of day, crash type, and so forth. However, variations existed across States both in the fields included on crash forms and in the precision with which a particular field was collected. Consequently, differing levels of detail were provided by the various States. For instance, not all States had a reliable indicator of whether a crash was speed related. Roadway width and shoulder type were similar across sites (11- to 12-ft lanes, earth/gravel shoulders), so these variables were not included in the analysis.
Table 47. Description of covariates.
Name |
Description |
Range |
Categorical Value |
|
|---|---|---|---|---|
SiteID |
Unique identifier for each site, used to account for repeated observations |
NA |
NA |
|
Volume |
Annual average daily traffic |
400 to 8,400 vpd |
NA |
|
Season |
Season of the year |
Categorical |
Winter | |
| Spring | ||||
| Summer | ||||
| Fall | ||||
SignType |
Type of sign |
Categorical |
0 |
control site |
1 |
speed sign |
|||
2 |
curve advisory sign |
|||
Tangent |
Posted speed limit |
50 to 65 |
NA |
|
Advisory |
Curve advisory speed limit |
None and 15 to 50 |
NA |
|
SpeedDiff |
differential of posted and advisory speed |
0 to 40 mph |
NA |
|
CurveType |
Type of curve |
Categorical |
0 |
isolated curve |
1 |
S-curve1 |
|||
2 |
Several closely spaced1 |
|||
Length |
Length of treatment or control section; accounts for different section lengths |
0.40 to 2.0 miles |
NA |
|
Period |
Installation period |
Categorical |
0 |
Control |
1 |
Before installation of sign |
|||
2 |
Install quarter or quarter when signs were not functioning |
|||
3 |
After sign installation |
|||
Radius |
Radius of curve |
138 to 5,953 ft |
NA |
|
Year-2004 |
Year after 2004, included to show trend over time |
Categorical |
NA |
|
NA = Not applicable
vpd = Vehicles per day
1About 500 ft or less spacing between curves
A simple analysis of the crash data was first conducted to assess general trends. Data were aggregated by State because sites within each State had similar before and after periods. Data were also aggregated overall. Crash rate per quarter was calculated using the equation in figure 72.
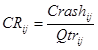
Figure 72. Equation. Calculation of crash rate per quarter.
Where:
CRij = crash rate per quarter for period j for State i.
Crashi = number of crashes for period j.
Qtrj = number of quarters for period j.
Change in crash rate per quarter was calculated by subtracting crash rate for the before period from the after period, so a negative number indicates a decrease in crash rate. Crash rate was calculated for total crashes and SV crashes. Results are similar given most crashes were SV crashes. Crash rate was compared by State and was compared across the entire study.
Table 48 shows results for both directions. The number of sites included in the analysis is also shown. A few sites had problems with data and were not included in the final analysis. As indicated, total crashes in the before period ranged from 0.10 to 1.02 crashes per quarter for control sites and from 0.13 to 1.14 for treatment sites. In the after period, total crashes per quarter ranged from 0.07 to 0.74 and 0.11 to 0.86 for treatment sites.
Two States had an increase in total crashes per quarter for control sites (Florida and Texas) from the before to after period while the remaining States had decreases ranging from 0.08 to 0.28. Two States (Florida and Texas) had an increase in total crashes per quarter (0.13 and 0.01) for treatment sites, with the remaining States having decreases that ranged from 0.16 to 0.64. In all States except Florida and Texas, treatment sites had much larger decreases in crash rates than the control sites.
Table 48 also provides crash rates for SV crashes for both directions. SV crashes for both directions ranged from 0.08 to 0.74 for control sites and 0.05 to 1.07 crashes per quarter for the before period. The SV crash rate ranged from 0.06 to 0.59 for control sites and 0.14 to 0.50 for treatment sites in the after period.
Florida experienced increases in SV crashes at control sites from the before to after period (with an increase of 0.17 crashes per quarter), with the remaining States having decreases from 0.02 to 0.15. All test States except Texas had decreases in SV crashes per quarter from the before to after period, ranging from 0.03 to 0.63 crashes per quarter. In many cases, the decrease in crash rate for treatment sites was two to three times that for the control sites.
Crash rate for total crashes for all control sites is 0.48 for the before period and 0.40 for the after period, with a change of -0.08 (17-percent decrease). Crash rate for total crashes for treatment sites is 0.55 before and 0.33 after, with a change of -0.22 crashes per quarter (40-percent decrease). The SV crash rate across sites is 0.38 for the before and 0.31 after for control sites, and 0.45 before and 0.24 after for treatment sites, resulting in change of -0.07 (19-percent decrease) for control sites and a -0.21 change for treatment sites (47-percent decrease). The decrease in crashes at treatment sites was 2.75 to 3.0 times higher than at control sites.
Table 48. Simple before and after comparison of crashes for both directions.
|
Number of Sites |
Before |
After |
Change |
||||
|---|---|---|---|---|---|---|---|---|
Total Crashes (crashes/qtr) |
SV Crashes (crashes/qtr) |
Total Crashes (crashes/qtr) |
SV Crashes (crashes/qtr) |
Total crashes/qtr (percent change) |
SV crashes/qtr (percent change) |
|||
Florida |
Control |
2 |
15 (0.50) |
10 (0.33) |
9 (0.56) |
8 (0.50) |
0.06 (13%) |
0.17 (52%) |
Treatment |
2 |
22 (0.73) |
16 (0.53) |
12 (0.86) |
7 (0.50) |
0.13 (18%) |
-0.03 (-6%) |
|
Arizona |
Control |
3 |
23 (0.55) |
22 (0.52) |
11 (0.41) |
10 (0.37) |
-0.14 (-25%) |
-0.15 (-29%) |
Treatment |
2 |
17 (0.61) |
14 (0.50) |
2 (0.11) |
1 (0.06) |
-0.50 (-82%) |
-0.44 (-89%) |
|
Washington |
Control |
3 |
43 (1.02) |
31 (0.74) |
29 (0.74) |
23 (0.59) |
-0.28 (-27%) |
-0.15 (-20%) |
Treatment |
2 |
32 (1.14) |
30 (1.07) |
9 (0.50) |
8 (0.44) |
-0.64 (-56%) |
-0.63 (-59%) |
|
Iowa |
Control |
6 |
44 (0.49) |
36 (0.40) |
26 (0.36) |
19 (0.26) |
-0.13 (-26%) |
-0.14 (-34%) |
Treatment |
4 |
34 (0.53) |
26 (0.41) |
12 (0.28) |
6 (0.14) |
-0.25 (-47%) |
-0.27 (-66%) |
|
Ohio |
Control |
3 |
6 (0.15) |
5 (0.13) |
2 (0.07) |
2 (0.07) |
-0.08 (-55%) |
-0.06 (-45%) |
Treatment |
3 |
24 (0.62) |
22 (0.56) |
10 (0.33) |
9 (0.30) |
-0.29 (-47%) |
-0.26 (-46%) |
|
Oregon |
Control |
5 |
36 (0.48) |
29 (0.39) |
17 (0.43) |
11 (0.28) |
-0.06 (-11%) |
-0.11 (-29%) |
Treatment |
4 |
26 (0.42) |
21 (0.34) |
6 (0.26) |
5 (0.22) |
-0.16 (-37%) |
-0.12 (-35%) |
|
Texas |
Control |
3 |
4 (0.10) |
3 (0.08) |
2 (0.11) |
1 (0.06) |
0.01 (8%) |
-0.02 (-28%) |
Treatment |
3 |
5 (0.13) |
2 (0.05) |
2 (0.14) |
2 (0.14) |
0.01 (11%) |
0.09 (179%) |
|
All sites |
Control |
25 |
171 (0.48) |
136 (0.38) |
96 (0.40) |
74 (0.31) |
-0.08 (-17%) |
-0.07 (-19%) |
Treatment |
20 |
160 (0.55) |
131 (0.45) |
53 (0.33) |
38 (0.24) |
-0.22 (-40%) |
-0.21 (-47%) |
|
SV = Single-vehicle
qtr = Quarter
Table 49 shows results for crashes that were in the direction of the sign for treatment sites and in the direction of the outside curve for control sites. As shown, the crash rate for total crashes per quarter was 0.08 to 0.74 for the before period and 0.0 to 0.56 for the after period for control sites. The crash rate for total crashes per quarter was 0.11 to 0.64 in the before period and 0.0 to 0.50 in the after period for treatment sites.
Iowa had an increase in crash rate of 0.23 for control sites, and Texas had an increase of 0.03. Decreases from 0.03 to 0.21 crashes per quarter at control sites were found for the other States. Florida, Iowa, and Oregon had minor increases in crashes (0.01 to 0.07) for the after period for treatment sites. The remaining States had decreases in SV crashes for treatments from 0.11 to 0.42 crashes per quarter. In most cases, the decreases were two to six times higher for treatment sites than control sites.
Before-installation results for SV crashes ranged from 0.05 to 0.45 crashes per quarter for control sites and 0.06 to 0.61 for treatment sites. After-installation SV crash rates ranged from 0.0 to 0.41 for control sites and 0.0 to 0.29 for treatment sites.
Results for control sites showed that one State (Iowa) had an increase of 0.11, and Texas had no change in SV crash rate from the before to after period, with the remaining States experiencing decreases from 0.04 to 0.20.
Results for treatment sites indicated that Florida had an increase in the SV crash rate of 0.06, and all other States had decreases from 0.01 to 0.44 from the before to after period. When decreases were noted, treatment sites had significantly greater decreases than control sites. Overall, treatment sites experienced decreases that where three to four times greater than those at control sites.
Results by direction were averaged across States, with crash rates of 0.28 for total crashes per quarter for control sites and 0.35 for treatment sites in the before period and 0.30 and 0.23 for the after period. This represents an increase of 0.02 crashes per quarter at control sites and a decrease of 0.12 at treatment sites (a 9-percent increase versus a 35-percent decrease). SV crash results for all sites show a crash rate of 0.22 for control sites and 0.29 for treatment sites in the before period, and 0.22 for control sites and 0.15 for treatment sites in the after period. This represents a decrease of 0.01 and 0.14, respectively (a decrease of 4 percent compared with 49 percent). The overall decrease in SV crash rate was 6 to 14 times higher for treatment sites than for control sites.
Descriptive statistics are provided to indicate overall trends. Caution should be used in applying the results, given that data were not normalized by season and more quarters of a particular season may have been present in the before period than in the after period. However, results show that, in general, a much greater decrease in crashes per quarter occurred at treatment sites compared with control sites.
Table 49. Simple before and after comparison of crashes for one direction.
|
Number of Sites |
Before |
After |
Change |
||||
|---|---|---|---|---|---|---|---|---|
Total Crashes (crashes/qtr) |
SV Crashes (crashes/qtr) |
Total Crashes (crashes/qtr) |
SV Crashes (crashes/qtr) |
Total crashes/qtr (percent change) |
SV Crashes/qtr (percent change) |
|||
Florida |
Control |
2 |
8 (0.27) |
6 (0.20) |
1 (0.06) |
0 (0.00) |
-0.21 (-77%) |
-0.20 (-100%) |
Treatment |
2 |
13 (0.43) |
7 (0.23) |
7 (0.50) |
4 (0.29) |
0.07 (16%) |
0.06 (26%) |
|
Arizona |
Control |
3 |
18 (0.43) |
17 (0.40) |
10 (0.37) |
9 (0.33) |
-0.06 (-14%) |
-0.07 (-18%) |
Treatment |
2 |
10 (0.36) |
8 (0.29) |
0 (0.00) |
0 (0.00) |
-0.36 (-100%) |
-0.29 (-100%) |
|
Washington |
Control |
3 |
31 (0.74) |
19 (0.45) |
22 (0.56) |
16 (0.41) |
-0.18 (-24%) |
-0.04 (-9%) |
Treatment |
2 |
18 (0.64) |
17 (0.61) |
4 (0.22) |
3 (0.17) |
-0.42 (-66%) |
-0.44 (-72%) |
|
Iowa |
Control |
6 |
17 (0.19) |
13 (0.14) |
18 (0.42) |
11 (0.26) |
0.23 (122%) |
0.11 (77%) |
Treatment |
4 |
17 (0.27) |
13 (0.20) |
12 (0.28) |
6 (0.14) |
0.01 (5%) |
-0.06 (-31%) |
|
Ohio |
Control |
3 |
4 (0.10) |
3 (0.08) |
0 (0.00) |
0 (0.00) |
-0.10 (-100%) |
-0.08 (-100%) |
Treatment |
3 |
19 (0.49) |
17 (0.44) |
7 (0.23) |
6 (0.20) |
-0.26 (-53%) |
-0.24 (-55%) |
|
Oregon |
Control |
5 |
25 (0.33) |
20 (0.27) |
12 (0.30) |
9 (0.23) |
-0.03 (-10%) |
-0.04 (-16%) |
Treatment |
4 |
12 (0.26) |
10 (0.22) |
6 (0.31) |
4 (0.21) |
0.05 (20%) |
-0.01 (-3%) |
|
Texas |
Control |
3 |
3 (0.08) |
2 (0.05) |
2 (0.11) |
1 (0.06) |
0.03 (44%) |
0.00 (8%) |
Treatment |
3 |
2 (0.11) |
1 (0.06) |
0 (0.00) |
0 (0.0) |
-0.11 (-100%) |
-0.06 (-100%) |
|
All Sites |
Control |
25 |
100 (0.28) |
80 (0.22) |
65 (0.30) |
46 (0.22) |
0.02 (9%) |
-0.01 (-4%) |
Treatment |
20 |
89 (0.35) |
73 (0.29) |
36 (0.23) |
23 (0.15) |
-0.12 (-35%) |
-0.14 (-49%) |
|
SV = Single-vehicle
qtr = Quarter
DEVELOPMENT OF CRASH MODIFICATION FACTORS USING A FULL BAYES MODEL
To study the effectiveness of various safety treatments, a before-and-after analysis was conducted using a Full Bayes model to develop CMFs. Expected crash rates are represented by safety performance functions (SPF) that relate the expected crash rate to traffic and road characteristics.
The Bayesian method accounts for regression-to-the-mean effects that result from the natural tendency to select treatment sites with high observed crash frequencies. Control sites were similar to treatment sites in terms of traffic volume, geometry, and location. A discussion of how treatment and control sites were selected is provided in chapter 2.
In the literature, SPF estimation in the context of before-and-after analysis has been conducted via the Empirical Bayes (EB) approach in conjunction with negative binomial model structure (Hauer et al. 2002; Hovey and Chowdhury 2005; Persaud and Lyon 2007; Elvik 2008). The estimated SPF is used to predict crash rates for treatment sites that would have occurred without the treatment (Hauer 1997). The predicted crash rates are then compared with the observed crash counts during the after period to develop CMFs.
Recently, the Full Bayesian (FB) method has gained a lot of interest because of the following advantages compared with the EB approach:
The dataset included 624 observations for control sites and 492 observations for treatment sites. Year was considered as covariate in the regression term to account for changes over time. Correlations between observations from the same section were accounted for as the within-subject errors in the model.
As noted in the Variables section earlier in this chapter, four separate models were developed: total and SV crashes in both directions and in the direction of the treatment/outside of curve. Quarterly crashes was the response variable. Crash counts across years and sites can be expressed by the general model (Congdon 2001) shown in figure 73.
![]()
Figure 73. Equation. Expression for crash counts across years and sites.
Where "trend" accounts for the effect of time, the "regression term" is of the same form as SPFs used in EB studies (Hauer et al. 2002, Persaud et al. 2002), and "random effect" accounts for latent variables across the sites. Correlations between observations from the same section were accounted for as the within-subject errors in the model.
Model Form and Selection Criteria
To find the appropriate model for the FB analysis, several models were tested. A zero inflated model (ZIP and ZINB) was evaluated against the plain count model (Poisson and Negative Binomial) followed by the Vuong test. Both zero inflated Poisson and Poisson-Gamma models were selected. Then, after applying the FB method, a deviance information criterion (DIC) was used to compare the different Bayesian hierarchical models (Spiegelhalter et al. 2003).
The models were developed using the equations shown in figure 74 and figure 75. Let Yi,t be the observed number of crashes at site i in year t, λi,t be the expected number of crashes at site i in year t, εi be the multiplicative random effect at site i, Xi,t be the corresponding covariates such as traffic and road conditions. The expressions for all models compared are listed as follows:
![]()
Figure 74. Equation. Model A (ZIP).
Where:
ln λi,t = α1 + X1'itβ1 + γ1 (t − 2004).
logit(πi,t) = α2 + X2i,tβ2 + γ2(t − 2004).
and
![]()
Figure 75. Equation. Model B (ZIP).
Where:
ln λi,t = α1 + X1'β1 + γ1 (t − 2004).
logit(πi,t) = α2 + X2'β2 + γ2(t − 2004).
εi~ Gamma(ø, 1/ø).
Prior Choices for FB Methodology
Prior distributions for parameters (α1, α2, β1, β2, γ1, γ2) are assumed non-informative N(0, 103) to reflect the lack of precise knowledge of the value of the coefficients. The prior distribution for parameter ø is assumed Gamma (1,1). The posterior distributions were calibrated using Monte Carlo Markov Chain (Gamerman 2006, Gilks et al. 1996) methods using all data from the control sites and the before period data for the treated sites.
The CMFs were calculated using the equation shown in figure 76.
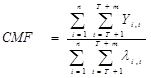
Figure 76. Equation. CMF calculation.
Where n is the number of treated sites, m is number of years after treatment, T is the last year before treatment, and λi,t is expected crashes without treatment for intersection i in year t in the after period. The corresponding standard error (STDE) for the CMF was calculated using the equation in figure 77.
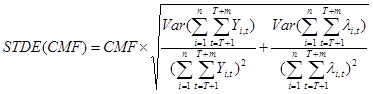
Figure 77. Equation. Calculation of standard error for the CMF.
The safety effect of installing the DSFS system was developed using the described methodology. As noted in the Variables section earlier in this chapter, four different models were developed: total and SV crashes in both directions, and total and SV crashes in the direction of sign or outside of curve. The best model was chosen with 95-percent significant covariates using DIC. Table 50 shows the parameter estimates for the best fit model for all crashes in both directions.
Table 50. Parameter estimations for ZIP model for total crashes in both directions.
Parameter |
Posterior Mean |
P-value |
|---|---|---|
Intercept |
-7.4295 |
< .0001 |
Log(volume) |
0.6456 |
< .0001 |
Length |
0.6784 |
< .0001 |
SpeedDiff |
0.0432 |
< .0001 |
S-curve versus. single curve |
-0.3602 |
0.0174 |
Multiple versus single curve |
0.1819 |
0.0002 |
Spring versus winter |
-0.1159 |
0.3239 |
Summer versus winter |
-0.3105 |
0.0202 |
Fall versus winter |
-0.3247 |
0.0128 |
2005 versus 2011 |
1.3004 |
< .0001 |
2006 versus 2011 |
1.0324 |
< .0001 |
2007 versus 2011 |
1.0054 |
< .0001 |
2008 versus 2011 |
0.8083 |
0.0005 |
2009 versus 2011 |
0.4502 |
0.0693 |
2010 versus 2011 |
0.8056 |
0.0005 |
Parameters for probability model |
||
Intercept |
-3.9830 |
0.0002 |
SpeedDiff |
0.1219 |
0.0003 |
Table 51 shows the parameter estimates for the best fit model for total crashes in the direction of the DSFS system for treatment sites and control sites.
Table 51. Parameter estimations for ZIP model for total crashes in one direction.
Parameter |
Posterior Mean |
P-value |
|---|---|---|
Intercept |
-8.0551 |
< .0001 |
Log(volume) |
0.6992 |
< .0001 |
Length |
0.7602 |
< .0001 |
SpeedDiff |
0.0278 |
0.002 |
S-curve versus single curve |
0.1061 |
0.5443 |
Multiple versus single curve |
0.4392 |
0.0463 |
Spring versus winter |
-0.3236 |
0.0460 |
Summer versus winter |
-0.3088 |
0.06604 |
Fall versus winter |
-0.5034 |
0.004 |
2005 versus 2011 |
1.2227 |
< .0001 |
2006 versus 2011 |
0.9846 |
0.0005 |
2007 versus 2011 |
0.9411 |
0.0009 |
2008 versus 2011 |
0.5879 |
0.0476 |
2009 versus 2011 |
0.2842 |
0.3684 |
2010 versus 2011 |
0.6984 |
0.0158 |
Parameters for probability model |
||
Intercept |
-1.1540 |
0.006 |
Table 52 shows the parameter estimates for the best fit model for SV crashes in both directions.
Table 52. Parameter estimations for ZIP model for SV crashes in both directions
Parameter |
Posterior Mean |
P-value |
|---|---|---|
Intercept |
-7.5668 |
< .0001 |
Log(volume) |
0.5629 |
< .0001 |
Length |
0.7287 |
< .0001 |
SpeedDiff |
0.0382 |
< .0001 |
S-curve versus single curve |
-0.3182 |
0.0578 |
Multiple versus single curve |
0.2889 |
0.0003 |
Spring versus winter |
-0.0413 |
0.6621 |
Summer versus winter |
-0.3927 |
0.0117 |
Fall versus winter |
-0.2790 |
0.0542 |
2005 versus 2011 |
1.7834 |
< .0001 |
2006 versus 2011 |
1.5176 |
< .0001 |
2007 versus 2011 |
1.3917 |
< .0001 |
2008 versus 2011 |
1.2045 |
< .0001 |
2009 versus 2011 |
0.8893 |
0.0048 |
2010 versus 2011 |
1.2391 |
< .0001 |
Parameters for probability model |
||
Intercept |
-4.3494 |
0.0053 |
SpeedDiff |
0.1238 |
0.0025 |
Table 53 shows the parameter estimates for the best fit model for SV crashes in the direction of the DSFS system for treatment sites or control sites.
Table 53. Parameter estimations for ZIP model for SV crashes in one direction.
Parameter |
Posterior Mean |
P-value |
|---|---|---|
Intercept |
-7.7523 |
< .0001 |
Log(volume) |
0.5269 |
< .0001 |
Length |
0.7984 |
< .0001 |
SpeedDiff |
0.0329 |
< .0001 |
S-curve versus single curve |
0.2163 |
0.2721 |
Multiple versus single curve |
0.6136 |
0.0398 |
Spring versus winter |
-0.3131 |
0.0936 |
Summer versus winter |
-0.3916 |
0.0502 |
Fall versus winter |
-0.5374 |
0.0071 |
2005 versus 2011 |
1.6955 |
< .0001 |
2006 versus 2011 |
1.4447 |
< .0001 |
2007 versus 2011 |
1.2980 |
0.0005 |
2008 versus 2011 |
0.8900 |
0.0226 |
2009 versus 2011 |
0.6567 |
0.1093 |
2010 versus 2011 |
1.0992 |
0.0040 |
Parameters for probability model |
||
Intercept |
-1.3295 |
0.0336 |
Table 54 lists the CMFs and associated parameters for the four models that were developed.
Table 54. Results for calculation of crash modification factors.
Crash Type |
Direction Type |
Observed Crashes |
Estimated Crashes |
CMF (STDE) |
95-Percent CI |
|---|---|---|---|---|---|
Total |
Both |
52.1 |
54.6 |
0.95 (0.01) |
0.93, 0.97 |
Total |
Toward sign or outside of curve |
32.5 |
34.8 |
0.93 (0.02) |
0.89, 0.97 |
Single-vehicle |
Both |
38.6 |
40.7 |
0.95 (0.01) |
0.93, 0.97 |
Single-vehicle |
Toward sign or outside of curve |
22.3 |
23.4 |
0.95 (0.02) |
0.91, 0.99 |
CMF =Crash mitigation factor
STDE = Standard error
CI = Confidence interval
Based on the estimated coefficients, predicted crashes per year after installing the DSFS system were calculated and are shown in table 54. The predicted number of crashes was calculated by estimating crashes for each quarter for each treatment site and summing the predicted crashes for the after period. CMFs were calculated by dividing the observed crashes by the predicted values.
For total crashes in both directions, the CMF is calculated as 52.1/54.6 = 0.95. In other words, total crashes for both directions are expected to decrease by 5 percent, and all crashes in the direction of the DSFS system are expected to decrease by 7 percent. SV crashes in both directions are expected to decrease by 5 percent, and SV crashes in the direction of the sign are expected to decrease by 5 percent.
To determine whether the reduction due to the treatment was significant or not, 95-percent CIs for the CMFs were calculated and are shown in table 54. For example, the 95-percent CI for all crashes in both directions is [0.95 ± 1.96 x 0.01] = [0.93, 0.97], not containing 1, so the crash reduction for all crash types is statistically significant.
Results of the statistical analyses indicate that the DSFS system results in a crash reduction from 7 to 5 percent.