U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-14-081 Date: November 2014 |
Publication Number: FHWA-HRT-14-081 Date: November 2014 |
The aim of this section is not to go in depth into the most commonly applied methodologies but rather to illustrate how they are applied in road safety research. Selected references are also provided where further information may be found.
The EB methodology for observational before-after studies is considered rigorous in that it accounts for regression-to-the-mean. In the process, SPFs are used and the use of these addresses the following:
In the EB approach, the change in safety for a given crash type at a site is given by the following:
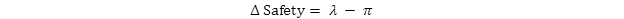
Figure 7. Equation. Change in safety using the EB approach.
Where:
λ = expected number of crashes that would have occurred in the after period without the strategy.
π = number of reported crashes in the after period.
In estimating λ, the effects of RTM and changes in traffic volume are explicitly accounted for using SPFs, relating crashes of different types to traffic flow and other relevant factors for each jurisdiction based on untreated sites (reference sites). Annual SPF multipliers are calibrated to account for temporal effects on safety (e.g., variation in weather, demography, and crash reporting).
In the EB procedure, the SPF is used to first estimate the number of crashes that would be expected in each year of the before period at locations with traffic volumes and other characteristics similar to the one being analyzed (i.e., reference sites). The sum of these annual SPF estimates (P) is then combined with the count of crashes (x) in the before period at a strategy site to obtain an estimate of the expected number of crashes (m) before strategy. This estimate of m is computed as follows:
![]()
Figure 8. Equation. Expected number of crashes before strategy implementation using the EB approach.
Where w is estimated from the mean and variance of the SPF estimate as follows:
![]()
Figure 9. Equation. Estimated weight using the EB approach.
Where k = constant for a given model and is estimated from the SPF calibration process with the use of a maximum likelihood procedure. In that process, a negative binomial distributed error structure is assumed with k being the overdispersion parameter of this distribution.
A factor is then applied to m to account for the length of the after period and differences in traffic volumes between the before and after periods. This factor is the sum of the annual SPF predictions for the after period divided by P, the sum of these predictions for the before period. The result, after applying this factor, is an estimate of λ. The procedure also produces an estimate of the variance of λ.
The estimate of λ is then summed over all sites in a strategy group of interest (to obtain ![]() ) and compared with the count of crashes observed during the after period in that group (
) and compared with the count of crashes observed during the after period in that group ( ![]() ). The variance of λ is also summed over all sites in the strategy group.
). The variance of λ is also summed over all sites in the strategy group.
The CMF (θ) is estimated as follows:
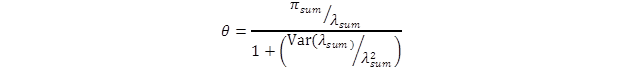
Figure 10. Equation. CMF estimate using the EB approach.
The standard deviation of θ is given by the following:
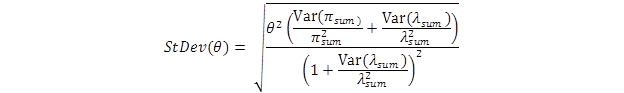
Figure 11. Equation. Standard deviation of the CMF estimate using the EB approach.
The percent change in crashes is calculated as 100(1 - θ); thus a value of θ = 0.7 with a standard deviation of 0.12 indicates a 30 percent reduction in crashes with a standard deviation of 12 percent.
Cross-sectional studies are particularly useful for estimating CMFs where there are insufficient instances where the treatment was applied to conduct a before-after study. For example, there may be few or no projects where the shoulder is widened, for example, from 4 to 6 ft. However, there would be many road segments with 4-ft shoulders and many with 6-ft shoulders. The reason that before-after studies are impractical in such cases is that there are often not enough before-after situations to allow for credible results.
In practice, it is difficult to collect data for enough locations that are alike in all factors affecting crash risk. Hence, cross-sectional analyses are often accomplished through multiple variable regression models. In these models an attempt is made to account for all variables that affect safety. If such attempts are successful, the models can be used to estimate the change in crashes that results from a unit change in a specific variable. The CMF is derived from the model parameters. The regression approach for estimating a CMF is consistent with the belief that the CMF is a function of the traits of the treated unit. A cross-sectional approach can be used to develop a CMFunction, and is preferable if the cause-effect relationship with crashes can be determined with confidence.
CMFs estimated from cross-section studies could be inaccurate for a number of reasons, including inappropriate functional form, omitted variable bias, or correlation of variables. It is common practice to use generalized linear modeling techniques, assuming a negative binomial error structure, to estimate multivariate crash prediction models. However, it is difficult to account for all factors that affect safety using such modeling techniques. For example, intersections with left-turn lanes also tend to have illumination. If a crash prediction model is used to estimate a CMF for left-turn lanes, and the presence of illumination is not accounted for in the model, the difference in model predictions with and without left-turn lanes could be partly due to illumination differences. Ironically, it is precisely because a variable is found to be correlated with another variable that it may be omitted during the model fitting exercise. Including correlated variables could in fact lead to effects that are counterintuitive (e.g., illumination increases night time crashes).
Case-control methods have been used in certain areas of highway safety, but few have focused on the effects of geometric design elements. For example, case-control studies have been applied to investigate the effectiveness of motorcycle-helmet use and the crash risk of hours of service for truck drivers. More recently, the case-control method was employed to estimate CMFs for geometric design elements, including lane and shoulder width. Case-control studies assess whether exposure to a potential risk factor is disproportionately distributed between the cases and controls, thereby indicating the likelihood of an actual risk factor.
The likelihood of an actual risk factor is expressed as the odds ratio between two levels of a variable. For example, it may be found that the odds of a crash occurring on horizontal curves with a degree of curvature greater than 15 degrees is 1.5 times the odds of a crash occurring on curves less than 15 degrees. The odds ratio is a direct estimate of the CMF. Risk factors may take the form of binary variables (e.g., median barrier, roadway lighting, or guiderail) or multi-level variables such as lane width (e.g., 9-, 10-, 11-, and 12-ft lanes). The sample is summarized by risk factor and case-control status to calculate the odds ratio. To illustrate the concept of the odds ratio, consider the data in table 2.
| Risk Factor | Number of Cases | Number of Controls |
|---|---|---|
| With | A | B |
| Without | C | D |
The odds ratio (CMF) is expressed as the expected increase or decrease in the outcome in question due to the presence of the risk factor. An odds ratio greater than 1.0 suggests that the presence of the risk factor increases risk, while a value less than 1.0 would suggest a decrease in risk. Using the notation in the table the odds ratio (OR) is calculated as:
![]()
Figure 12. Equation. Odds ratio calculation.
Case-control studies cannot be used to measure the probability of an event (e.g., crash, severe injury, etc.) in terms of expected frequency. They are more often used to show the relative effects of risk factors. Statistical analyses, such as multiple logistic regression techniques, are commonly used to clarify these relationships because they are able to examine the risk associated with one factor while controlling for other factors.
Finally, the case-control method cannot demonstrate causality because there is no time sequence of events in the analysis. Instead, the odds ratio indicates the increased likelihood of a crash occurring when a risk factor (e.g., roadway characteristic is present. It does not, however, recognize differences between locations with many crashes or a single crash. This is a loss of potentially important information and thus, the true increase in risk could be underestimated.