U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-16-036 Date: April 2016 |
Publication Number: FHWA-HRT-16-036 Date: April 2016 |
This chapter describes the propensity scores-potential outcomes framework that was used to estimate the safety effectiveness of the CGT intersection relative to a traditional signalized T intersection. The propensity scores estimation method, matching methods, and the potential outcomes estimation method are described in this chapter. An observational before-after evaluation (using the empirical Bayes (EB) method) could not be used in the present study, because the CGT intersections were either constructed as such or the conversion from a traditional signalized T intersection to a CGT intersection took place long ago, precluding the availability of electronic crash data from the before period. Recent research has shown that the propensity scores-potential outcomes framework produces safety effect estimates (i.e., CMFs) that are nearly identical to EB observational before-after and cross-sectional statistical models when treatments are deployed at locations that were not selected for countermeasure implementation based on high crash frequencies.(11) Because the CGT is an intersection form that is constructed to improve traffic operations when site conditions permit, and because only after data were available for analysis (i.e., no crash data were available when the intersections may have operated either under a different configuration or with different control), the analysis is therefore not subject to site-selection bias. Thus, it is assumed that the propensity scores-potential outcomes framework will produce results equivalent to the EB method.
The propensity scores-potential outcomes methodology used in the study controlled for the following:
Randomized experiments are considered the gold standard for determining the causal effects of treatments. Well-conducted randomized experiments yield unbiased estimates of average treatment effects because there is no correlation between the treatment and all other important covariates, other than the outcome of interest (i.e., there is no confounding).(12,13) Thus, methods that remove correlation between the treatment and other important predictor (independent) variables in observational studies lead to estimates of treatment effects that are similar to the results of a randomized experiment.
Propensity score analysis can be used to mimic randomized experiments by using observed covariates to estimate the probability that an observation received a treatment (i.e., the propensity score).(14) Propensity scores can be viewed as a scalar summary of the multivariate covariates, and balancing the true propensity score will lead to balance of all observed covariates.(14) In the context of traffic safety, examples may include the probability that an at-grade intersection contains lighting (or not) based on site-specific features such as traffic volume, type of traffic control, and level of pedestrian demand. Another example may be the probability that a roadway segment contains a horizontal curve as a function of traffic volume, lane width, and roadside geometry. The estimated propensity scores are then used to match treated and untreated observations.(15,16) This process removes correlation between the treatment and observed covariates. When propensity score matching is paired with regression analysis (performed after matching), selection bias is reduced.
Binary logit or probit models are commonly used to estimate propensity scores.(9,15,16) The estimated propensity scores should include all variables that could potentially be relevant to the treatment. As such, the variables included in the propensity score model should not be selected based on statistical significance.(9,17,18) Since the goal of propensity score analysis is to remove correlation between the treatment and other potentially important predictor variables, the functional form of the variables in the propensity score model should be selected based on which functional form yields the best matching results.
The following assumptions are associated with propensity score analysis:(9,15,16)
The propensity score for a treatment was estimated in the present study using binary logit regression, which is specified in the equation in figure 3.(19)
![]()
Figure 3. Equation. Binary logit model for propensity scores.
Where:
xi= A set of covariates for entity i (i.e., intersection safety-influencing features such as average annual daily traffic (AADT), the intersection skew angle, and the intersection’s location (if any) on a horizontal curve).
β = A vector of parameters to be estimated.
p(i) = The propensity score for entity i.
The standard error for the propensity score can also be calculated. The formula for the standard error of a binary logit is specified as seen in the equation in figure 4. (20)
![]()
Figure 4. Equation. Binary logit standard error.
Where:
n = The sample size used to estimate the propensity score.
SE(pn(i)) = The standard error of the propensity score for entity i.
In traffic safety evaluations, it is common to assess the quality of model fit using the McFadden Pseudo R-squared (ρ2), which is analogous to the R-squared value used to express the goodness-of-fit of an ordinary least squares regression model, where higher values indicate a better fit to the data, and can take a value between 0 and 1. It is expressed as seen in the equation in figure 5:(19,21)
![]()
Figure 5. Equation. Psuedo R-squared goodness-of-fit.
Where:
L(full) = Log-likelihood of the model with explanatory variables.
L(0) = Log-likelihood of the intercept-only model.
However, the best model when using matching, within the propensity scores-potential outcomes framework, is the model that yields the best covariate balance, not the model with the best ρ2 value.
Numerous algorithms exist for propensity score matching. Among them are nearest-neighbor (NN) matching, K-nearest neighbor matching, radius matching, kernel matching, and Mahalanobis matching.(9,15,16) The optimal method for matching is dependent on the available data. Typically, either caliper-based NN or Mahalanobis matching is used.(16) Either 1:1 (one treated to one untreated) matching or 1:n (1 treated to n untreated) matching can be done using either NN or Mahalanobis matching. If the sample sizes of the treated and untreated groups are similar, 1:1 matching is often an appropriate choice. (16)
Other issues related to propensity score matching relate to allowing replacement (permitting a comparison or untreated entity to be matched to more than one treated entity) and eliminating data for use in the potential outcomes estimation.(9,15,16) Discussion of these issues follow descriptions of the NN and Mahalanobis matching algorithms in the following subsections.
The first step in NN matching is to randomly order the data.(9) If the data are not randomly ordered and there are multiple observations with the same propensity scores, the results may be biased.(15) Once this is done, it is possible to use either 1:1 or 1:n matching. When closeness of the match is critical (how similar the matched entities are based on the estimated propensity score), or the sample size of the two groups are similar, 1:1 matching is preferred.(16) On the other hand, 1:n matching increases the total sample size, leading to lower standard errors in regression estimates of the potential outcomes (with potentially smaller standard errors than in simple cross-sectional analysis of the data). (22) However, this often comes at the expense of making the treated and comparison groups less comparable.(16) Issues related to replacement are described in more detail in the following sections.
When using NN matching, the differences between treated and untreated observations may be small or large. In order to account for large differences, two things should be considered. First, the data should be checked for common overlap (the distribution of propensity scores that is shared between the treated and comparison groups). Second, use of calipers or confidence intervals (CIs) should be used to ensure that differences between matched treated and untreated observations are not significantly dissimilar.(9,15,16)
Specifying a caliper width ensures that all matched observations will have a maximum propensity score difference within the range of the caliper width. Common caliper widths used are 0.25 or 0.20 multiplied by the standard deviation of the propensity scores within the treated group.(9,16)Other caliper widths can be used as long as the standardized bias in the matching results is not too large (typically assumed to be greater than 0.25 or 0.20). Larger caliper widths allow increased selection bias to remain in the data due to larger differences between the treated and comparison groups. Smaller caliper widths minimize the differences between the treated and comparison groups but often come at the expense of dropped observations.(16) However, it has been shown that with large datasets, the treatment effects estimates do not change significantly as the caliper width changes.(23)
Once the matching criteria have been established, the treated observations are matched to the untreated observations with the most similar propensity score (within the caliper width or CI).(9,15,16) If replacement is allowed, a single untreated observation can be copied and matched to multiple treated observations if it has the nearest propensity score. If replacement is not permitted, then each untreated observation may only be used once. After matching has occurred, unmatched treated and comparison observations are dropped from the dataset and not used in the potential outcomes.(9) The results should then be checked, and the standardized bias for the unmatched data and the matched data should be compared.(9) The standardized bias indicates whether the matching was effective in achieving covariate balance.
Mahalanobis matching uses the same algorithm as NN matching with one difference: the treated observations are matched to the untreated observations with the closest match based on multiple variables, not just the propensity score.(16) The closest match based on multiple variables uses the Mahalanobis distance. This method may specify that the untreated observations available for matching to a treated observation be within a specified caliper or CI based on the propensity score, but this is not required as long as the matching results lead to small values of standardized bias.(9,15,16) As with NN matching, the data should be randomly ordered prior to matching. The Mahalanobis distance is calculated using the equation in figure 6.(16)
![]()
Figure 6. Equation. Mahalanobis distance.
Where:
![]() = The Mahalanobis distance matrix between groups x and y (i.e., treated and untreated groups) using the variables specified for the matching.
= The Mahalanobis distance matrix between groups x and y (i.e., treated and untreated groups) using the variables specified for the matching.
![]() = The matrix of the differences in values between groups x and y for the variables included in the matching.
= The matrix of the differences in values between groups x and y for the variables included in the matching.
S = The covariance matrix between x and y.
The propensity scores can be included as one of the variables in the Mahalanobis distance along with other important matching variables.
Genetic matching is a sequential process that optimizes covariate balance by finding the best matches for each treated entity.(16) The genetic matching process minimizes imbalance across the covariates; therefore, it optimizes covariate balance.(24) This is accomplished by minimizing a general Mahalanobis distance defined in figure 7.(24)
![]()
Figure 7. Equation. Genetic matching distance.
Where:
GMD= The genetic matching distance.
S-1/2= The Cholesky decomposition of S (i.e., S = S-1/2(S-1/2)T).
W = The weighting matrix.
With genetic matching, both the propensity score and other covariates can be included in the matching scheme. The iterative process uses Kolmogorov-Smirnov (K-S) statistics to measure covariate balance in addition to standardized bias measures.(24) Genetic matching results in optimal matches but often does so at the cost of high computation times.(16)
Replacement is defined as allowing a single untreated observation to be replicated and matched to multiple treated observations. Allowing replacement may be beneficial when the amount of common overlap (portion of distribution of propensity scores shared by the treated and comparison groups) is not sufficient to produce good matching or when a significant amount of dropped observations would result if replacement is not permitted. When there is only a moderate amount of common overlap, replacement reduces the amount of dropped observations and is likely to reduce the amount of bias in the data.(16) When there is a significant amount of common overlap, matching without replacement is preferred.(16)
Dropped observations can result from poor common overlap and from narrow caliper widths. Dropped untreated observations often occur when matching. However, restricting caliper widths will result in treated observations being dropped from the analysis sample when no untreated observations have propensity scores within the acceptable range for matching. The tradeoffs between caliper width, replacement allowance, and the number of dropped observations must be considered in the propensity scores-potential outcomes framework. When caliper width is increased, the standardized bias (discussed in the next subsection) could increase, which will also increase the sample size used in the analysis (i.e., fewer dropped observations resulting from matching). An increased sample size often leads to greater statistical power (i.e., smaller standard errors of the estimates). It has been shown in previous research that when the standardized bias is kept within a small maximum value (usually 0.20 to 0.25), and the sample size is maximized, the matched estimates of treatment effects can yield unbiased estimates of the treatment effects that have smaller standard errors than an unmatched sample.(22)
As noted previously, standardized bias should be checked for propensity scores and other important covariates to assess the quality of covariate balance achieved from matching. The equation in figure 8 is used to compute the standardized bias.(9)
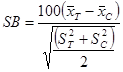
Figure 8. Equation. Standardized bias.
Where:
SB = The standardized bias.
![]() = The sample mean of the treated group for variable x.
= The sample mean of the treated group for variable x.
![]() = The sample mean of the comparison group for variable x.
= The sample mean of the comparison group for variable x.
![]() = The sample variance of the treated group for variable x.
= The sample variance of the treated group for variable x.
![]() = The sample variance of the comparison group for variable x.
= The sample variance of the comparison group for variable x.
Before-after matching comparisons of standardized bias for the propensity score and other covariates provide an indication of the improvement in covariate balance resulting from matching on the propensity score. A standardized bias with an absolute value of 20 or smaller indicates no statistical difference between the treated and comparison groups (i.e., they are equivalent).(16)
It has also been pointed out that even when the mean and standard error two groups are similar, the distributions of the two groups may still be significantly different due to different distributional shapes.(25) Thus, a K-S test is also used to assess covariate balance.(26) The K-S test compares the cumulative frequencies of two samples. Based on this comparison, the statistical fit of the two distributions is estimated.(27) This test uses the maximum difference (Dn) between the two distributions to estimate the statistical fit. The distance is calculated using figure 9.(27)
![]()
Figure 9. Equation. K-S test.
Where:
Max= Maximize function.
Fn(xi) = The cumulative distribution function (CDF) of the treated group for variable x at value i.
Sn(xi) = The CDF of the untreated group for variable x at value i.
The p-values for the K-S tests are obtained from a standard mathematical table.(27) This test can be used to test the covariate balance for any covariate of interest.
In summary, the present study estimated the propensity scores using a binary logistic regression model. The propensity scores compare the probability that a signalized intersection in the pool of observations is a CGT form versus a traditional signalized intersection based on the covariates (e.g., traffic volume, intersection skew angle, and presence of horizontal curve). NN matching was first used to match each CGT intersection (treatment site) to a traditional signalized intersection (comparison site). If, based on the reduction of the standardized bias in the covariates among the matched data, acceptable matching was not produced, then Mahalanobis matching was used. Replacement was permitted when matching to minimize the amount of dropped data from the analysis sample.
After matching treated (CGT) and untreated sites (conventional signalized T intersections), the potential outcomes (crash frequency) were estimated using count regression models. The use of Poisson regression to model crash frequency was introduced in 1986.(28) Negative binomial regression, a general form of Poisson regression that accounts for overdispersion, was later used to estimate crash frequencies in the traffic safety literature.(29,30) Negative binomial regression was used to develop the safety performance functions in the first edition of the Highway Safety Manual (HSM).(31) However, the standard Poisson and negative binomial models do not account for serial correlation, which results when crash data are recorded annually at a site over a period of years, and these repeated observations are the analysis unit (i.e., annual expected crash frequency is the dependent variable in a statistical model). Thus, the standard errors for the regression results using these models were likely underestimated.
Regression models that account for the count nature of crash frequency data, serial (spatial or temporal) correlation, and correlation between variables in the model (e.g., major and minor road traffic volumes) and that can estimate parameters for variables that do not vary over time include mixed effects negative binomial and Poisson models.(21,32) Since this study used data with correlation between variables included in the model, the data included yearly data (repeated measurements) for each of the intersections and the variable of interest (if it was a CGT intersection or not), all of these issues were present in this study. A discussion of each of these models follows.
The mixed effects negative binomial allows parameters to be fixed or random when specifying the model.(21) The inclusion of random parameters corrects for serial correlation while allowing estimation of an overdispersion parameter to capture the effects of within-cluster overdispersion (i.e., when the variance of crashes is greater than the mean for each individual intersection). The log-likelihood function for the mixed effects negative binomial is shown in figure 10.(33)
![]()
Figure 10. Equation. Mixed effects negative binomial log-likelihood.
Where:
uk = The random intercept/slope for entity k.
yk = The outcome for entity k.
q = The number of covariates included in the model.
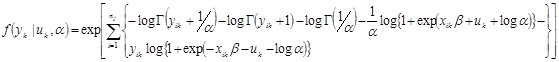
β = The vector of coefficients.
α = The overdispersion parameter.
A mixed effects negative binomial regression model with only the intercept allowed to be random is known as a random intercept model.(21) If all parameters are specified to be random, the model is known as a random parameters model. The mixed effects model is sometimes referred to as a random parameter or random coefficient model, even if some of the parameters are specified as fixed parameters.(21) When multiple parameters are allowed to be random, the model adds more adjustment for overdispersion into the model than the mixed-effects Poisson or the random intercept negative binomial. Thus, the model must be checked to ensure that it is not adjusting for more correlation than is warranted in the data.(21) This can be done by assessing the statistical significance of the overdispersion parameter as well as using a chi-square test to assess if the mixed effects model is preferred to a standard negative binomial regression. The null hypothesis for the chi-square test is that the mixed effects model does not fit the data better than the standard negative binomial regression.
When multiple random coefficients are used, the variance function for a mixed effects model is difficult to derive. However, for the case of a random intercept negative binomial, the variance function (for observation i) is specified as seen in figure 11.(33)
![]()
Figure 11. Equation. Mixed effects negative binomial variance function.
Var = The variance.
μ = The expected mean.
σ = The standard deviation of the random intercept.
α = The overdispersion parameter.
When the overdispersion parameter is not statistically significant, the mixed effects negative binomial regression model reduces to a mixed effects Poisson model. The expected mean for observation i, based on the random intercept negative binomial model, is given as seen in figure 12.(32)
![]()
Figure 12. Equation. Mixed effects predictions.
Where:
ζ i = The random intercept for observation i.
xi= The vector of variables for observation i.
When a mixed effects model is used for prediction, the mean values of the estimated random parameters are used as the constant for the prediction model.
The mixed effects Poisson model is the same as a mixed effects negative binomial model but without overdispersion within clusters (a cluster for this study is defined as multiple repeated measurements at the same intersection over time). The log-likelihood for the mixed effects Poisson is shown in figure 13.(33)
![]()
Figure 13. Equation. Mixed Poisson log-likelihood.
Where:
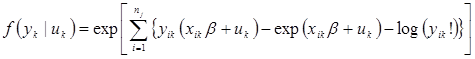
In figure 13, the subscript i refers to the observation, while all other variables and subscripts are defined in figure 10 and figure 12. In the context of this study, the observation i refers to a year associated intersection or entity k.
The variance function for a mixed effects Poisson model with the random term limited to the intercept only (random intercept Poisson) is specified using the equation in figure 14.(32)
![]()
Figure 14. Equation. Mixed effects Poisson variance function.
The expected mean value for an observation using a random intercept Poisson model is found using the equation in figure 12.
CMFs derived from regression models in the propensity scores-potential outcomes framework are estimated using the coefficient for the treatment indicator variable (included in the model) as the exponent of the base number e. The formula for this is shown in figure 15.
![]()
Figure 15. Equation. Regression CMF estimation.
Where:
CMFTreatment = The CMF for the treatment.
βTreatment = The estimated coefficient for the treatment.
It should be noted that figure 15 uses the regression coefficient for the treatment indicator variable, which is included in the mixed effects Poisson or negative binomial regression model.
The 95-percent CIs for CMFs using count models are calculated using the equation in figure 16.
![]()
Figure 16. Equation. Regression CMF confidence interval.
Where:
CI95% = The 95-percent CI.
σTreatment = The standard error of βTreatment from the regression model.
Because traffic safety evaluations often estimate CMFs using a cross-sectional regression model, the present study also utilized this approach with all of the observations as a means of comparison to the propensity scores-potential outcomes framework. The cross-sectional model did not use any matched data and was estimated using a mixed-effects negative binomial regression model, which was previously described. The cross-sectional statistical model was specified using the form shown in figure 12. In the model, an indicator variable (CGT versus conventional signalized T intersection) was included in the specification to assess the safety performance of the CGT relative to the conventional signalized T intersection.