U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-16-054 Date: October 2016 |
Publication Number: FHWA-HRT-16-054 Date: October 2016 |
A literature search identifying current practices in analyzing motorcycle crash data assessed the applied statistical methods and data used. The Transportation Research Information Service (TRIS) and International Transport Research Documentation databases were the primary resources for published research involving statistical analysis of motorcycle safety. TRIS includes the capability to search several databases, including the Highway Research Information Service database for domestic literature, the Highway Research in Progress database for ongoing research studies, and the International Road Research database for international literature. Additionally, the project team searched the national and international contacts for relevant research from local and State agencies that are not published or otherwise not widely available.
As expected, the review of literature found that, by far, the most widely used analytic methods applied to motorcycle safety data belong to the family of discrete outcome models. Such models are applied for estimating the impact of crash and/or behavioral characteristics on the type of crash that occurs. For example, a discrete choice model may predict the probability of a given level of severity, given that a crash has occurred, with predictor variables describing the rider, motorcycle, and roadway (e.g., use/non-use of helmet, engine size, type of roadway, or speed limit). It is important to note that such models do not provide an estimate of the expected crash frequency and cannot be directly applied for developing SPFs or CMFs. (They can, however, be used to develop severity distribution functions that can be applied to an SPF for total crashes, if such an SPF exists, to estimate crash frequency by severity.)
The review is divided into sections on crash frequency models, discrete choice “probabilistic models,” and models that do not clearly fit either category. A summary of key findings appears at the end of this chapter.
Where motorcycle crash frequency models exist, they have the most direct relevance to the development of motorcycle-specific SPFs and CMFs. These models can be used to estimate expected crashes or to estimate CMFs through cross-section studies or before-after studies. The literature provides few examples of developing models to predict motorcycle crash frequency. The literature review identified four such studies regarding developing crash frequency models in recent years. A review of these studies follows.
Flask et al. applied a fully Bayesian multi-level fixed effects model to estimate expected multi-vehicle motorcycle crash frequencies on road segments in Ohio.(1) Three datasets were used in this study. The Ohio Department of Transportation provided the first dataset, which was composed of 32,289 interstate, U.S. route, and State route segments. This dataset included the following variables: pavement type, lane width, shoulder width, number of lanes, median presence, horizontal and vertical curve-related statistics, the overall vehicle average daily traffic (ADT), and segment length. In addition to the roadway segments, township information was available, including the number of lane-miles, area of the township, and the urban status of the township. All of these variables were considered as fixed effects parameters with the exception of the ADT and segment length, which were assumed to have a linear relationship with crashes.
U.S. Census data provided demographic information for the different regions of Ohio, such as the percentage of residents over the age of 65, percentage of residents under the poverty level, and the mean travel time to work. In addition to demographic information, the county population, number of motorcycle endorsements (motorcycle licenses), and number of registered motorcycles were used as measures of motorcycle and motor vehicle traffic and were compiled at a regional level. Spatial correlation through conditional autoregressive random effects were included in the model and were shown to reduce the model error by adding the prior knowledge of neighboring regions and segments, leading to better parameter estimates. The distance between neighbors was measured using the distance between two segments in any direction. Random effect terms may be used to reduce model error that is caused by unavailable or unrecorded data, such as motorcycle-specific vehicle-miles traveled (VMT) or motorcycle AADT. Variables found to affect motorcycle crashes in addition to total AADT included the number of lane miles in a township, urban versus rural area type, the number of motorcycle endorsements, county population, and mean travel time to work reported by county.
Including the spatial random effects in the Flask et al. model reduced model error due to the unavailability of motorcycle AADT data in the dataset, but the resulting model would not provide the same benefits if applied to another jurisdiction.(1) The consideration of spatial correlation will account for unobserved correlation in motorcycle volumes at nearby locations, but that is specific to the dataset the model is developed with.
French and Gumus studied the relationship between motorcycle fatalities and economic activity using Fatality Analysis Reporting System (FARS) data.(2) The U.S. Bureau of Economic Analysis and the U.S. Bureau of Labor Statistics provided data on real income per capita and unemployment rate, respectively. Other potential explanatory variables included motorcycle registrations, rural VMT, urban VMT, alcohol taxes, average temperature and precipitation, gasoline prices, and data on safety programs affecting motorcycle riders (e.g., introduction of a helmet law). Total fatal crashes and crashes disaggregated by crash type, day, time, and level of rider’s blood alcohol concentration (BAC) were studied with fatalities per 100,000 population as the dependent variable. The project team used a generalized linear model with log-link function and included both year and State fixed effects. Each State-year observation was weighted by the square root of the State population. Among the findings, estimates suggested a 10-percent increase in real income per capita is associated with a 10.4-percent increase in motorcycle fatality rates.
Haque et al. sought to identify factors affecting motorcycle crashes at three- and four-legged signalized intersections in Singapore by developing Bayesian crash prediction models.(3) Explanatory variables included intersection geometry and total traffic volume. It is important to note that due to the high use of motorcycles in Singapore, it is likely that motorcycle volume is highly correlated to total traffic volume. Other variables besides traffic volumes affecting expected crash frequency included number of lanes, presence of wide median, uncontrolled left-turn lane, presence of exclusive right-turn lane, and presence of red-light cameras (RLCs).
Manan et al. developed a generalized linear model with negative binomial error structure to predict fatal motorcycle crashes on Malaysian primary roads.(4) Explanatory variables included motorcycle AADT and access points per hour (kilometer). Separate models using total AADT and motorcycle AADT were calibrated. The model using total AADT had slightly better overall goodness-of-fit measures, including an overdispersion parameter of 0.821 compared to 0.872 for the model using motorcycle AADT. However, the model using motorcycle AADT demonstrated some improvement in a cumulative residuals (CURE) plot versus access points per kilometer, indicating that the model was less biased with respect to access point density. The authors rightly point out that the model with motorcycle AADT would be more sensitive to modal shifts. According to the authors, a model with both motorcycle and non-motorcycle volumes was not attempted because the two measures were so closely correlated with a Pearson’s correlation coefficient of 0.913.
By a large margin, most of the literature on modeling motorcycle crashes uses discrete choice models. This family of models predicts the probability of an outcome given that a crash has occurred based on the values of explanatory variables. Researchers focused on motorcycle safety typically apply discrete choice models to estimate the impact of both road user and roadway variables on the likelihood of a specified outcome severity given that a crash occurs. For example, researchers may examine the impact of helmet use or roadway curvature on the severity of crashes.
Within the family of discrete choice models, there are many different modeling approaches, but these are essentially based on two different types of models: unordered or ordered discrete outcome models.
For unordered models, logistic regression models (sometimes referred to as “logit models”) are used to refer specifically to the problem in which the dependent variable is binary (only two possible outcomes), while problems with more than two categories are referred to as “multinomial logistic regression.”
For ordered models, multiple categories are possible and are considered to be ordered in some logical way, such as severity data on the killed, A injury, B injury, C injury, and property damage only (PDO) (KABCO) scale. By considering crash severity as ordered, it is not assumed that the difference between an O and C crash is the same as between a B and K crash, for example. These models may be ordered logit or ordered probit, where the difference is the assumed distribution of the model error term and link function.
The following subsections illustrate examples of three discrete choice models applied to the study of motorcycle safety. The review is by no means comprehensive, given that the focus of the project (and the review) is on crash frequency modeling and the sheer volume of literature on crash severity modeling necessitated some selectivity.
Logistic regression models identify factors that affect the likelihood of an outcome—such as a crash resulting in a fatality—and can be used to predict the outcome of an event. Logistic models apply when only two outcomes are possible. Figure 1 displays a logistic model.
![]()
Figure 1. Equation. Logistic model.
Where:
P(Y = 1) = The probability that the outcome was observed.
![]() = The characteristics of the person, crash, etc.
= The characteristics of the person, crash, etc.
ß = The parameters of the model to be estimated.
In estimating the model parameters, figure 2 shows the LN of the odds (i.e., the logit).
![]()
Figure 2. Equation. Logistic model parameter estimation.
The odds ratio is defined as the probability of the outcome occurring divided by the probability of the alternate. For example, if the probability of a fatality in the event of a crash were 1/10 , then the odds ratio would be (1/10) / (9/10) = 0.11. Taking the exponent of the estimated parameters reveals the amount by which the odds ratio increases or decreases as the independent variable changes by one unit.
Kim et al. developed a logistic regression model to explain the likelihood of alcohol impairment among crash involved motorcycle riders in police reported motorcycle crashes.(5) The basic logistic model is shown in figure 3.
![]()
Figure 3. Equation. Kim et al. logistic regression model.(5)
Where:
Pr(I) = The probability of impairment.
a = The parameters of the model to be estimated.
A = Age of rider.
W = Weekend occurrence.
N = Nighttime occurrence.
O = Non-resident status.
The developed models also attempted additional variables. Results indicated that impairment was more likely to be a factor for middle-aged riders, unlicensed riders, and riders who did not wear a helmet and that impairment-related crashes are more likely to occur at night, on weekends, and in rural areas.
Connor applied logistic regression to motorcycle fatality data where coroner and police reports were available and license endorsement status was known.(6) The goal was to find what characteristics increased the likelihood that a fatal motorcycle crash involved an unendorsed rider. These characteristics included single-vehicle crashes, younger drivers, and driver's license suspensions in the past 7 years.
Akaateba et al. applied logistic regression to roadside observations of helmet use at 12 randomly selected sites.(7) The authors estimated odds ratios, adjusted odds ratios, and 95-percent confidence intervals for variables associated with helmet use. Female riders as well as riding during the weekdays and morning periods and at locations within central business districts showed higher helmet wearing rates.
Gabauer developed logistic models to predict rider injury for motorcyclists impacting longitudinal barriers.(8) Rider characteristics such as helmet usage and alcohol involvement were found to have a larger influence on injury severity in comparison to associated roadway characteristics.
Theofilatos and Yannis investigated the relationship between stated attitudes and behaviors with respect to safety and crash involvement of motorcyclists in Europe based on a survey.(9) Principal component analysis of the 38 variables collected through the survey grouped variables that showed a similar variance and effect on the probability of having been in a crash. A logistic regression model was used to model the probability of having been in a crash as a function of the declared attitudes and behaviors, age and declared exposure.
Keall et al. used a case-control study design to quantify fatality risks for motorcyclists based on BAC.(10) The authors acquired case (i.e., crash) data from police reports and post-mortem data. Control data were collected roadside including BAC tests. The authors used a logistic regression to model the data. The results show a much higher risk of fatality, even at low levels of BAC. At a BAC of 0.03, the fatality risk was 3 times higher; at a BAC of 0.08, the fatality risk was 20 times higher.
Haworth et al. applied a case-control approach to collecting data for 222 motorcycle crashes (cases) and 1,195 non-crash involved (controls) motorcyclist trips past a crash site at the same time of day and day of week of crash occurrence.(11) Data collection included detailed information of each crash, a comparison of features of cases and controls, and motorcycle exposure information. The controls comprised three groups. One group included riders who did not stop. A second included riders who stopped and were interviewed roadside. A third group included riders who gave a roadside interview and a follow-up interview. Odds ratios were estimated through conditional logistic regression. The approach was termed “conditional” because cases were matched to their controls by day, time, and location, and other confounding variables such as age were included in the model as explanatory variables. Some of the factors found to increase crash risk included age under 25, never married, unlicensed, increased BAC, use of a sidecar, motorcycle engine over 750 cc, and rider not being the owner of the motorcycle.
Kim and Boski developed a logistic regression model for the probability of being at fault in a crash for motorcyclists and drivers using temporal, roadway, and environmental factors.(12)
Multinomial logistic (or logit) models apply when more than two outcomes are possible and there is no ordering to the outcomes. A multinomial logistic model is shown in figure 4.
![]()
Figure 4. Equation. Multinomial logistic model.
Where:
P(Y = i) = The probability that the outcome, i, was observed given the family of possible outcomes, I.
![]() = The characteristics of the person, crash, etc.
= The characteristics of the person, crash, etc.
ß = The parameters of the model to be estimated.
Each possible outcome, i, has its own set of explanatory variables and parameters, otherwise known as the “utility function.”
Mannering and Grodsky developed a multinomial logit model to determine what factors significantly influence motorcyclists’ estimates of their likelihood of becoming involved in an accident if they continue to ride for 10 more years.(13) A questionnaire was used to collect data characterized by four categories: rider characteristics (e.g., age), exposure (e.g., miles driven per year), experience (e.g., years of having a motorcycle license), and behavioral attributes (e.g., a stated preference for consistently exceeding the speed limit). The questionnaire responses on the riders’ estimate of their likelihood to be involved in a crash in the next 10 years were grouped into low (0 to 20 percent), medium (30 to 70 percent), and high (80 to 100 percent).
The model predicted the likelihood of a response given the characteristics represented in the model. The model is shown in figure 5.
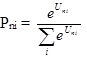
Figure 5. Equation. Multinomial logistic response model.
Where:
Pni = The probability that rider n would categorize themselves as having a low, medium, or high risk of being in an accident in the next 10 years.
Uni = Linear function of variables which determine the probability of a rider considering themselves in the low-, medium-, or high-risk group.
Among the studies’ findings was that age, gender, and experience were significant determinants of the estimate of self-risk and that riders were generally aware of their relative crash risks.
In a follow-up study, Shankar and Mannering presented a multinomial logit model for rider injury severity in single-vehicle crashes, considering environmental roadway and vehicle factors.(14) Using data for Washington, relationships were found between crash severity and motorcycle displacement, rider age, alcohol impaired riding, rider ejection, speed, rider attention, pavement surface, and type of highway.
Building on the Shankar and Mannering research, Savolainen and Mannering built multinomial logit models of severity separately for single- and multi-vehicle motorcycle crashes in Indiana and found important differences for the two crash types.(15) In general, they revealed several factors leading to more severe injuries, including poor visibility (horizontal curvature, vertical curvature, and darkness), unsafe speed (citations for speeding), alcohol use, not wearing a helmet, right-angle and head-on collisions, and collisions with fixed objects. Wet pavement conditions, locations near intersections, and passengers on motorcycles were associated with severe crashes, suggesting motorcyclists may be managing risks.
Jung et al. examined factors associated with motorcyclist fatalities. The research found that a lack of or improper use of helmets, victim ejection, alcohol/drug effects, collisions (i.e., head-on, broadside, and hit-object), and truck involvement were more likely to result in fatal injuries regardless of age group.(16) Weekend and non-peak hour activity were found to have a strong effect on both the younger and older age groups. The authors determined that two factors—movement of running off the road preceding a collision and multi-vehicle involvement—were statistically significant factors in increasing motorcycle fatalities among drivers in the older age group. Use of street lights in the dark decreased the probability of severe injury for older motorcyclists. Being the driver (as opposed to passenger), being the at-fault driver, being on a local road, and committing a speed violation were significant factors in increasing the fatalities of younger motorcyclists. Road conditions and collision location factors were not statistically significant to motorcyclist fatalities.
Jones et al. applied multinomial logistic models to analyze factors affecting the injury severity outcome of motorcycle crashes.(17) The variables affecting motorcycle crashes were grouped by common characteristics into four categories: motorcyclist, crash, environment, and roadway. Crashes in the vicinity of large vehicles, around roadway curves, and in rural areas increased the likelihood of severe crash outcomes.
Geedipally et al. estimated multinomial logit models to identify differences in factors likely to affect the severity of crash injuries of motorcyclists.(18) Key findings showed that alcohol, gender, lighting, and presence of both horizontal and vertical curves played significant roles in injury outcomes of motorcyclist crashes in urban areas. Similar factors were found to have significantly affected the injury severity of motorcyclists in rural areas, but older riders (older than 55), single-vehicle crashes, angular crashes, and divided highways also affected injury severity outcomes in rural motorcycle crashes.
Ordered probit and logit models are similar to logistic models. As with unordered models, probit and logit models have different assumptions for the error term distribution and link functions. These models determine which factors significantly affect the probability of the outcome of an event and can be used to predict the likelihood of each possible outcome of an event but differ in that they differentiate unequal differences between ordinal categories in the dependent variable (e.g., it does not assume that the difference between no injury and minor injury is the same difference as between a severe injury and a fatality given a unit change in an explanatory variable).
In the multiple response case, figure 6 displays the ordered model.
![]()
Figure 6. Equation. Ordered probit model.
Where:
y = The ordinal for the outcome data.
x = A vector of variables determining the discrete ordering for each observation.
ß = A vector of estimable parameters.
μi and μi-1 = The upper bound and lower bounds for injury severity i, respectively.
The modeling process estimates both the vector or parameters and the upper and lower bound limits.
Barrette et al. studied the impacts of changes to the Michigan universal helmet use law using an ordered probit model.(19) The degree of injury severity sustained by crash-involved motorcyclists before and after Michigan’s transition from a universal to a partial helmet law was examined. The models controlled for a variety of rider, roadway, traffic, and weather characteristics and indicated that helmets reduced the probability of fatalities by more than 50 percent.
Ariannezhad et al. applied ordered logit models to study the factors contributing to crash severity of motorcycle crashes on suburban roads.(20) The results indicated that there are several factors that increase the severity of motorcycle crashes. Factors include weekends, winter and fall, dawn, foggy and clear weather, non-administrative areas, riders older than 60 years old, riders without a proper license, lack of helmet, motorcycle at-fault, speeding, overtaking, collisions with buses, and heavy vehicle, pedestrian, and single-vehicle crashes. Additional factors increasing severity included head-on crashes, fatigue and sleepiness, rules violation, road imperfection, and curvature.
Wang et al. applied ordered probit models to injury severity of single-vehicle motorcycle crashes on curved roadways.(21) Results indicated that curve radius is a significant factor influencing injury severity of single-motorcycle crashes along horizontal curved roadway segments. The authors estimated that an increase of 1,000 ft in curve radius decreases the likelihood of fatalities and serious injuries by 0.2 and 0.15 percent, respectively, in single-motorcycle crashes along a curved roadway section. The authors also found that speeding and hit-object increased the likelihood of higher severities.
Blackman and Haworth applied ordered probit models to compare the crash risk and crash severity of motorcycles, mopeds, and larger scooters.(22) Greater motorcycle crash severity was associated with higher (>50 mi/h (80 km/h)) speed zones, horizontal curves, weekend, single-vehicle, and nighttime crashes. Moped crashes were more severe at night and in speed zones of 56 mi/h (90 km/h) or faster. Larger scooter crashes were more severe in 43-mi/h (70-km/h) zones than in 37-mi/h (60-km/h) zones but not in higher speed zones, and they were less severe on weekends than on weekdays.
The literature review revealed several other analysis methods, which were applied to motorcycle safety evaluation.
Haque et al. developed log-linear models of motorcycle crash risk.(23) Log-linear models can be used to identify conditions that increase crash risk or severity and to estimate odds multipliers that express the increased or decreased risk associated with a change in a variable or interactions of variables in the model. Conventionally, contingency tables, which record the number of responses for each combination of variable values, are used. However, when the number of variables is greater than two, the process can be arduous. A log-linear model predicts the frequency of crashes for each combination of levels of explanatory variables. The frequency predicted is the number of crashes meeting the levels of each variable out of all crashes observed. This should not be confused with predicting the expected crash frequency on the roadway. For example, one category may be male riders, aged 25 to 44, with a BAC over 0.08. The frequency of crashes meeting these criteria would be predicted. The authors used quasi-induced exposure to account for exposure. In this approach, it is assumed that the presence of not-at-fault riders in the crash data represent the general population. The relative exposure for not-at-fault riders within the population of two-vehicle crashes is their crash frequency divided by the total population crash frequency. The authors then calculated the relative risk (RR) by dividing the respective odds ratios by the odds ratios for exposure under the same conditions.
Chin and Haque investigated the effects of RLCs on motorcycle crashes.(24) Quasi-induced exposure was applied using not-at-fault riders involved in right-angle crashes. Results showed that an RLC reduced the relative crash vulnerability or crash-involved exposure of motorcycles at right-angle crashes. Log-linear models were also developed and indicated that light and heavy vehicles were more likely to experience a right-angle crash with a motorcycle at non-RLC locations than intersections with RLCs.
de Rome et al. studied the effectiveness of protective clothing by recruiting motorcyclists involved in crashes through hospitals and repair services and then conducting interviews.(25) Hospitalization and injury were modeled using Poisson regression with log-link function to estimate the RR controlling for confounding variables. RR can be interpreted as the likelihood of the outcome without the variable of interest present divided by the likelihood of the outcome with the variable present. For example, the RR of an injury while wearing a helmet would be the ratio of injury crashes to non-injury crashes for riders not wearing helmets to the ratio of injury to non-injury for riders wearing helmets. The use of motorcycle jackets, pants, and gloves reduces the likelihood of hospitalization, as well as risk of upper body injury, hands/wrists, and feet/ankles.
Huang and Lai applied survival analysis using Cox regression models to identify risk factors for time until death comparing single-vehicle crashes for both alcohol- and non-alcohol-related crashes.(26) Survival analysis essentially models the probability that if one has survived until time t, then they will succumb to the event (in this case death) in the next instant. Cox regression models account for the effects of various covariates on the likelihood of survival and the results. The results show the impact each covariate has on the risk (in this case, the risk of death). Factors increasing risk of death for motorcycle riders included older age, crashing into trees, nighttime riding, curved roads, and local roads.
Chung applied boosted regression trees to classify single-vehicle motorcycle crashes into fatal or non-fatal crashes.(27) The output of the analysis indicated which variables contributed most to correctly classifying crashes, thus indicating which had the greatest impact on crash severity.
As noted earlier, the vast majority of motorcycle crash research used probability models to identify factors associated with crash severity outcomes. These models are not directly relevant to the estimation of CMFs and SPFs; however, the research was selectively reviewed because of the potential for applying probability models to crash frequency models for total crashes to estimate crash frequency by severity type.
The limited international research does suggest that motorcycle crash frequency models can be developed based only on total AADT for all vehicle types. However, the project team researched jurisdictions where motorcycle volume constitutes a sizable proportion of and is strongly correlated with the total traffic volume. The one significant study from the United States that developed crash frequency models for road segments did not use motorcycle volume as a variable due to the unavailability of these data. Instead, the number of motorcycle endorsements (motorcycle licenses) and number of registered motorcycles were used as surrogate measures of motorcycle and motor vehicle traffic, but these could only be compiled and applied at a regional level. In addition, spatial random effects modeling reduced model error due to the unavailability of motorcycle AADT data. However, the fact that this benefit is specific to the Ohio dataset modeled suggests that the developed models will not be easily transferable to another jurisdiction. Nevertheless, the research does suggest that there is promise in seeking alternatives to directly including motorcycle volumes in motorcycle crash frequency prediction models.
The literature review found very few studies focused on the prediction of crash frequency but many studies concerned with motorcycle safety. Crash frequency models are required for developing SPFs and CMFs. Table 1 provides a brief summary of the methods reviewed, including the data required, outcomes, uses, strengths, and limitations.
| Method | Data Required | Outcomes | Uses | Strengths | Limitations |
|---|---|---|---|---|---|
| Discrete choice | Crash data and presence or absence of feature of interest | Estimates the increased likelihood of dependent variable being present, given a crash has occurred, as a function of explanatory variables | Useful for identifying risk factors and comparing the RR between two or more factors | Advanced statistical methods are available; can often be accomplished using only readily available crash record data | Does not provide an estimate of crash frequency |
| Count frequency | Crash data, exposure data, and geometric data | Provides an estimate of expected crash frequency; CMFs can be inferred from parameter estimates | Useful for estimating CMFs and developing predictive models for before-after studies and network screening | Advanced statistical methods are available | Modeling can be difficult for rare crash types; exposure is the biggest influence of expected crashes, but motorcycle volumes are often unavailable |
| Log-linear/contingency table | Crash data and presence or absence of feature of interest | Estimates the increased likelihood of dependent variable being present, given a crash has occurred, as a function of explanatory variables | Useful for identifying risk factors and comparing the RR between two or more factors | Advanced statistical methods are available; can often be accomplished using only readily available crash record data | Does not provide an estimate of crash frequency |
| Quasi-induced exposure | Crash data | Estimates the relative presence of units (i.e. motorcyclists) in a population | Can be used as an estimate of motorcycle exposure in the absence of volume data | Requires only crash data to apply | Cannot be used as an estimate of motorcycle exposure at specific locations |
| RR/Poisson model | Crash data and presence or absence of feature of interest | Estimates increased risk of event without a variable of interest present compared to when it is present | Useful for identifying risk factors and comparing the RR between two or more factors | Requires only crash data to apply | Does not provide estimate of crash frequency |
| Survival analysis/Cox regression | Crash data and presence or absence of feature of interest | Estimates the effect a variable has on the risk of an event occurring | Useful for identifying risk factors and comparing the RR between two or more factors | Requires only crash data to apply | Does not provide estimate of crash frequency |
| Boosted regression trees | Crash data and presence or absence of feature of interest | Classifies crashes and indicates which variables influence this classification | Useful for identifying risk factors and determining which most affect the outcome of interest | Requires only crash data to apply | Does not provide estimate of crash frequency |