Investigating the Impact of Lack of Motorcycle Annual Average Daily Traffic Data in Crash Modeling and the Estimation of Crash Modification Factors

Chapter 3. Analysis Methods

The project team developed and undertook a number of analytical approaches in order to do the following:

• Explore how much predictive power for an SPF is lost when motorcycle volumes are unknown and how this lack of information may affect a study of motorcycle countermeasures estimating a CMF.
  
  
• Explore alternative methods for deriving accurate predictions of motorcycle crashes or motorcycle volume data.

This chapter provides an overview of each analysis method and a discussion of which research goal(s) were met by its application. The project team pursued modeling of motorcycle crash data on several fronts that are helpful in casting light on the two research questions.

The methods applied may be broadly classified into two groups: avenue A and avenue B. The methods for avenue A focus on investigating the difference in predictive performance for motorcycle SPFs calibrated with motorcycle AADT versus total AADT only. The methods for avenue B focus on the difference in CMF estimates found when using motorcycle AADT versus total AADT only.

Avenue A Methods

The three methods applied in avenue A focus on the impact of the lack of motorcycle AADT on modeling motorcycle crashes and the development of tools for those jurisdictions lacking these data. The methods make use of statewide databases for States that have motorcycle AADT estimates available. The following section discusses the three methods, all of which involve the estimation of predictive models. Table 2 summarizes the details of these methods for quick and easy reference throughout this report.

FHWA = Federal Highway Administration.

All models were calibrated using generalized linear modeling (GLM) using the R software. GLM allows the specification of various error structures. The negative binomial error structure is recognized as an appropriate form for modeling crash data. The negative binomial overdispersion parameter (the inverse of the shape parameter provided by R), which is estimated in the modeling process, can be used in the comparative assessment of models fit to the same data in that a smaller value indicates a better fit model. Crash counts at sample sites are used as estimates of the dependent variable, which is the expected number of crashes per year while corresponding road characteristics and traffic data are used as estimates of the independent variables.

Model Type A1

The purpose of model type A1 is to explore how much predictive power is lost when motorcycle volumes are unknown and how this lack of information would affect an evaluation of motorcycle countermeasures. The approach is to first develop SPFs for several road classes for motorcycle crashes with and without motorcycle volumes. The performance of each SPF pair, with and without motorcycle volumes, is then evaluated across the range of motorcycle AADTs to assess the overall goodness-of-fit to the data, as well as ranges of motorcycle AADTs and any other variables to identify circumstances where the lack of motorcycle AADT may cause the model to perform poorly. Assessment measures, in addition to the overdispersion parameters, include mean absolute deviation (MAD), adjusted R² values, and CURE plots described in subsequent paragraphs.

MAD gives a measure of the average magnitude of variability of prediction. Smaller values are preferred to larger values. MAD is the sum of the absolute value of predicted minus observed crashes divided by the number of sites, as shown in figure 7.

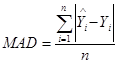
Figure 7. Equation. MAD.

Where:

n = Validation data sample size.

Fridstrom et al. introduced a modified R² value.⁽²⁸⁾ This goodness-of-fit measurement subtracts the normal amount of random variation that would be expected even with a perfectly specified model. As a result, the amount of systematic variation explained by the model is measured. Larger values indicate a better fit to the data. Values greater than 1 indicate that the model is overfit, and some of the expected random variation is incorrectly explained as the systematic variation. Figure 8 shows the calculation.

Figure 8. Equation. Modified R² goodness-of-fit measure.

Where:

y_i = Observed counts.
= Predicted values from the SPF.
= Sample average.
.

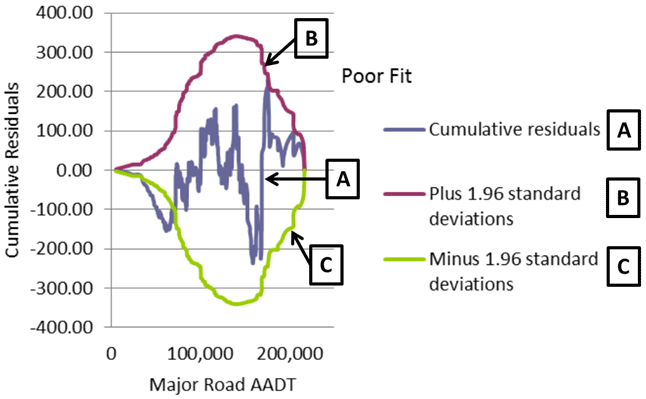
For an SPF to produce useful estimates, it must be good for all values of every variable. An alternative tool to describe goodness-of-fit is the CURE plot. A CURE plot is a graph of the cumulative residuals (observed minus predicted crashes) against a variable of interest sorted in ascending order. Long trends (increasing or decreasing) indicate regions of bias that should be rectified through model improvement either by the addition of new variables or by a change of functional form. Large vertical changes in the CURE plot invite the examination of outliers. The CURE plot is useful in determining whether an SPF is acceptable and in comparing multiple SPFs. The following steps are used to construct a CURE plot:

• Step 1: Sort sites in ascending order of the variable of interest so that N is the number of sites, n is an integer between 1 and N, and S(n) is the cumulative sum of residuals from 1 to n.
  
  
• Step 2: For each site calculate the residuals, res, as the observed minus predicted crashes.
  
  
• Step 3: For each site calculate the CURE, S(n), which is the sum of residuals from 1 to n.
  
  
• Step 4: For each site calculate the squared residuals, res².
  
  
• Step 5: For each site calculate the cumulative squared residuals, σ² (n), which is the sum of squared residuals from 1 to n.
  
  
• Step 6: Sum the cumulative squared residuals over all sites, σ² (N).
  
  
• Step 7: For each site, estimate the variance of the random walk using the equation in figure 9.

Figure 9. Equation. CURE plot variance estimate.

• Step 8: For each site, calculate the 95-percent confidence limits using the equations in figure 10 and figure 11.

Figure 10. Equation. Lower limit of 95-percent confidence interval.

Figure 11. Equation. Upper limit of 95-percent confidence interval.

• Step 9: Plot the CURE S(n) and the 95-percent confidence limits on the y-axis against the explanatory variable of interest on the x-axis. Figure 12 displays an example CURE plot for the variable major road AADT. In this example, the model is performing relatively well, as the CURE remain within the 95-percent confidence limits over most of the range, only crossing outside the boundary limits for a short range of lower AADT. The areas outside the boundary limits indicate a poor fit as indicated in the figure. If the graph of CURE was in that area frequently, then this would indicate the presence of model bias.

©Persaud and Lyon.

Figure 12. Graph. Example CURE plot.

The project team used two comparative measures to assess the CURE plots for competing models. One is the maximum CURE deviation, which has a value of 237 at an AADT of 159,000 in the figure 1 example. The other is percent CURE deviation, which is defined as the percent of the range of the x-axis variable for which the CURE plot is outside the 95-percent confidence limits. In figure 12, this occurs between AADTs of approximately 35,000 and 70,000; about 16 percent of the individual data points lie outside the 95 percent confidence limits.

It is also of particular interest to assess how well the models predict motorcycle crashes for high-crash locations, as these sites are the ones typically of interest in treatment applications that would form the basis for future CMF development. To do this, sites are ranked first by the crash counts per mile in one period; the Empirical Bayes (EB) estimates based on the calibrated SPFs and crash counts in that period for the highest ranked locations are then compared to crash counts for these locations in a subsequent period.

Model A1 was applied because it provides a direct measure of how the predictive power of a model is affected by either including or excluding motorcycle volumes. By using the same data for both sets of models, the impact of motorcycle volumes on predictive power was assessed directly without any biases. The use of CURE plots also allows this assessment to be broken down by ranges of motorcycle volumes.

Model Type A2

The purpose of model type A2 is to develop a relationship between motorcycle crash frequency and total crash frequency as a function of traffic volumes for the two vehicle categories. Models were calibrated for both motorcycle and total crashes using traffic volumes for motorcycles and all vehicles, respectively. Then, a relationship between the SPFs for the two crash types can be inferred from the motorcycle SPF prediction using the total crash SPF prediction as an explanatory variable. If successful, this relationship could then be applied to the SPF for total crashes for another State to infer an SPF for motorcycle crashes for that State. In turn, that SPF can be used in the evaluation of retrospective and prospective before-after evaluations of the effects on motorcycle crashes of infrastructure countermeasures. The assessment of success uses similar measures (MAD, etc.) as for assessing model type A1.

Model A2 was applied because, if successful, it would allow jurisdictions without motorcycle volumes to predict motorcycle crashes based on SPFs for total crashes. The limitation of the approach is that the models may not transfer well between jurisdictions that differ in terms of factors influencing motorcycle VMT and riding patterns.

Model Type A3

The purpose of investigating model type A3 was to attempt the development of models to estimate motorcycle traffic volumes based on roadway characteristics and other variables that may influence motorcycle trip generation. For the latter, information on motorcycle registrations, licensing, and sociodemographic variables was collected. If successful, these models could be used to estimate motorcycle volumes in similar jurisdictions. Due to differences in weather, motorcycle riding culture, commuter versus recreational riding, and other factors affecting motorcycle volumes between jurisdictions, it will be important to identify which of these factors need consideration when determining the applicability of a model. The assessment of success used similar measures as for assessing model type A1.

The project team applied this approach because, if successful, it would allow jurisdictions to directly estimate motorcycle volumes. If the important factors influencing motorcycle VMT can be identified and included in the models developed, this approach should provide for better model transferability than model type A2.

Avenue B Methods

The methods applied in avenue B focus on the impact of the lack of motorcycle AADT on the estimation of CMFs. These methods make use of simulated data. Simulating data creates a database with many locations and with assumed relationships between roadway geometry or other countermeasures and motorcycle crashes. The ability to accurately measure this “true” relationship is then tested when motorcycle volumes are and are not used in the process. The fixed relationships affecting motorcycle crashes were determined considering a likely range of values based on existing safety knowledge.

To investigate the impact of the lack of motorcycle AADTs on the estimation of CMFs, twoCMF estimation approaches were investigated: B1, the EB before-after approach, and B2, cross-sectional generalized linear models.

For the EB before-after approach, one or more countermeasures were assumed with a known value of its CMF. The simulated database was divided into two time periods, and the after period expected crash means for each location is adjusted by the value of the CMF. The new after period counts are then generated from the Poisson distribution. The EB approach was then applied to the data for these treated sites, using the remaining sites as a reference group. This was done once using the motorcycle AADTs and once for total AADT. A comparison was then made to see how the lack of motorcycle AADT affected the estimate of the CMF and its variance. This entire process, beginning with the simulated data, was performed multiple times and with multiple sample sizes so that conclusions could be made with confidence and have broad applicability.

For the cross-sectional regression model approach, an assumed relationship, based on logical considerations and related research, was defined between one or more geometric variables and added to the SPFs developed in model A1. The relationship was defined in terms of a CMF. This modified SPF was then used to simulate the data as described above. GLM was then used to re-estimate the SPF, including the fictional variable, using motorcycle AADT and then using total AADT only. A comparison was then made to see how the lack of motorcycle AADT affected the estimate of the CMF and its variance.

This entire process, beginning with the simulated data, was performed multiple times so that conclusions could be made with confidence.

This approach for avenue B was applied because it provided a direct measure of how the lack of motorcycle AADT affects CMF estimation by replicating the process of estimating CMFs. The use of simulated data provides a realistic and unbiased dataset for making this assessment. The limitation is that the true relationships between motorcycle AADT and crashes and geometric features and crashes need to be assumed. However, the knowledge gained in avenue A using real data informed these decisions.