U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-17-082 Date: December 2017 |
Publication Number: FHWA-HRT-17-082 Date: December 2017 |
Before–after and cross-sectional regression analyses are the two most common methodologies for developing CMFs for installed countermeasures using crash data. The preferred before–after method relies on recent countermeasure installations. This method uses the safety performance at a treatment site before countermeasure installation to predict what would have happened at the site without the countermeasure. Hauer’s Observational Before–After Studies in Road Safety on before–after evaluations is still the primary guidance for those types of studies.(5) A cross-sectional analysis develops an equation to predict the number of crashes at highway locations, where the equation contains a term for the countermeasure of interest. Before–after studies have an advantage in that using the before-period data to predict what would have happened reduces much of the site-to-site variation that must be accounted for with cross-sectional regression analysis. Thus, before–after studies can provide powerful results with relatively low sample sizes when data are available from the specific timeframe and certain biases are mitigated.
The project team selected a before–after analysis for this evaluation due to the availability of RCUT treatment sites.
Hauer describes four primary before–after analysis methods, each accounting for a different type of bias.(5) The following provides an overview of the four methods.
Naive analyses only adjust for a difference in the number of years of crash data from the before period to the after period.(5) Naive analyses are not trustworthy when more serious biases may be present. Therefore, the naive analysis results are not presented.
Adjustments for changes in traffic volume are a standard feature of many crash studies, as traffic volume is highly related to crash frequency. The method is described in Chapter 8 of Hauer.(5) Adjusting for traffic volume accounts for some threats to study validity; however, this method does not account for other events that would cause a bias in study results. Therefore, the project team relied more heavily on the results from other methods in drawing conclusions.
Many CMF studies do not report the results from an analysis adjusting for traffic volume. However, it is an important step when using comparison groups to account for simultaneous event bias (detailed in the following section) does not include an adjustment for changing traffic volumes. Hauer does not provide a method for estimating the CMF and the standard deviation (SD) of the CMF while adjusting for both comparison groups and changing traffic volume.(5) For the purpose of this study, the project team analyzed the adjustment for traffic flow and the adjustment for comparison groups separately.
As detailed in the following chapters, traffic volumes in the dataset were fairly constant and experienced small changes across years at most sites over the study period. This may be due to stable volumes at the sites or a result of traffic volume estimates based on interpolations from relatively rare field counts. Due to the small changes in traffic volume from year to year and a lack of calibrated safety performance functions for signalized intersections in each of the four studied States, the project team assumed a proportional relationship between crashes and volume for this evaluation. Additionally, the traffic volume adjustment method should properly consider a coefficient of variation in the traffic volume data, which is a measure of how much traffic volumes at the site vary from day to day. Coefficients of variation were not available for the treatment sites in this evaluation, so the project team used a middle range value of 0.1 for the calculations.(5)
One of the most important potential biases to a before–after crash study are events that occur during the study periods at the treatment sites that change the predicted number of crashes regardless of the treatment. Common simultaneous event biases include significant weather events like hurricanes or ice storms and changes in vehicle and crash reporting characteristics. To account for simultaneous event biases, the project team used comparison sites as described by Hauer.(5) The team identified four potential comparison sites for each treatment site. Potential comparison sites were large surface street intersections (to ensure adequate sample sizes) near the treatment site (to ensure that the same events occurred at both places). Aerial photographs were reviewed to ensure the sites did not undergo any discernible treatment during the study period.
Hauer recommends testing potential comparison sites prior to an analysis.(5) The test consists of calculations of odds ratios of the changes in crash frequency at the treatment sites and potential comparison sites from one year to the next before the countermeasure was installed. If this calculation is performed over a series of years before the treatment was installed, a look at the mean of the odds ratios and the SD of the mean will be revealing. The mean should be close to 1.0—and the SD close to 0—for successful comparison sites that are tracking closely to the treatment sites in the years before countermeasure installation. This concept is illustrated in figure 4.
Figure 5 illustrates how the CMF is estimated using the comparison group method.(5)
Where:
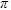 = predicted crashes in the treatment group in the after period had the treatment not been implemented.
= predicted crashes in the treatment group in the after period had the treatment not been implemented.
M = crashes in the comparison group before the implementation of the treatment.
N = crashes in the comparison group after the implementation of the treatment.
K = crashes in the treatment group before the implementation of the treatment.
Figure 6 illustrates the next step in the process.
Where 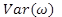 is variance of the sequence of sample odds ratios that are calculated based on the time series of crash counts from the treatment and comparison sites.
is variance of the sequence of sample odds ratios that are calculated based on the time series of crash counts from the treatment and comparison sites.
As mentioned by Hauer, for an ideal comparison group, the mean of the odds ratios is very close to 1, and is very close to 0.(5) Figure 7 and figure 8 show how to estimate the CMF and variance.
Where:
![]() = crashes in the treatment group after the implementation of the treatment.
= crashes in the treatment group after the implementation of the treatment.
Var ( 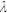 ) = assuming reasonably that the crash frequency follows a Poisson distribution.
) = assuming reasonably that the crash frequency follows a Poisson distribution.
The project team used a before–after analysis with comparison sites for this evaluation. The method accounts for simultaneous event biases, which the project team thought to be the most threatening potential bias to the evaluation. The method relies on high-quality comparison sites, but, as mentioned, the quality of the comparison sites is testable and is provided later in this report.
Before–after studies most commonly use the EB method to account for regression-to-the-mean bias. Regression to the mean is the tendency of an abnormally high or low value recorded in one time period to return to a value much closer to the long-run average in the next time period. This is important in most safety studies because transportation agencies typically install countermeasures at high-crash locations and must account for regression to the mean in the after period. Fortunately, regression to the mean was not an important threat to the validity of this evaluation because the treatment sites were not chosen on the basis of any type of hazardous site identification process. Instead, the agencies selected the sites for RCUT installation primarily to relieve congestion. Therefore, the project team did not employ the popular EB method described in Chapter 11 of Hauer.(5) With complex intersections spread over four States, an EB analysis would have been very complicated for this evaluation. The comparison site method proposed herein efficiently accounted for the most important potential study bias—simultaneous events—using comparison sites that passed a quality test. Chapter 4 describes this comparison site method in detail.