U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-13-090 Date: April 2016 |
Publication Number: FHWA-HRT-13-090 Date: April 2016 |
This chapter provides a description of the methods used in this study to compute axle loading defaults.
The focus of this study was to develop alternate MEPDG traffic loading defaults based on the LTPP SPS TPF WIM data. The main traffic loading default is NALS. Other defaults that are based on WIM data are APC, axle spacing, and wheelbase.
NALS defaults are used when site-specific NALS are not available or are of limited quality. Two types of situations may be encountered for the pavement design project location: no knowledge of the loading conditions or limited knowledge of traffic loading conditions at the project site. The default NALS developed in this study were designed to provide traffic loading alternatives for these situations.
NALS developed in this study are grouped in the following two tiers:
Tier 1 NALS defaults are useful for sites that have no information regarding expected traffic loading. These defaults represent an average traffic loading condition observed at the 26 SPS TPF sites.
The benefit of tier 2 defaults is that they provide users with multiple choices for selecting traffic loading conditions for different truck classes and axle group types. This allows pavement designers to simulate different loading scenarios and select scenarios that best describe the expected traffic loading conditions at the design site. This tier 2 approach for specifying defaults is a significant improvement over the scope of defaults currently available in the MEPDG software; however, use of these defaults requires some knowledge about the traffic loading condition expected at the pavement design site. This knowledge may be obtained through short-term truck surveys, portable WIM measurements, interviews with personnel involved in freight and commodity analyses, and discussions with law enforcement personnel engaged in monitoring truck weight violations.
The development of MEPDG traffic loading defaults started with the selection of WIM sites that satisfied data selection criteria and development of representative NALS for each of these sites. Then, NALS from selected individual sites (or all the sites, in the case of global defaults) were averaged to compute defaults. Based on this approach, the methodology for development of the MEPDG traffic loading defaults includes the following tasks:
Specific methods to accomplish these tasks are described in the following sections.
MEPDG NALS inputs represent the expected axle load frequency distributions by vehicle class and axle group type for a typical day of a month. Since seasonal changes in axle load frequency distributions are not uniform across different States and are likely to be observed only on the roads that carry a large percentage of seasonal loads, default values are developed to represent axle load frequency distributions for a typical day of the year. If truck loads change seasonally due to truck volume changes, monthly adjustment coefficients are used to adjust truck volumes between different months. Therefore, before defaults NALS could be developed, RANALS for individual sites must be computed.
The purpose of RANALS is to accurately represent RANALS for a given site. These RANALS should not only accurately characterize axle loading condition observed at a given site but be representative for development of the default axle loading conditions (i.e., spectra based on low axle counts may be accurate for the site but insufficient for development of a well-defined axle load spectrum for computation of the default).
Several approaches for computing RANALS were considered, and the advantages and disadvantages of each were analyzed. In the end, the approach for computing RANALS based on representative monthly NALS considering all available years was selected. This approach resembles the approach for computing AASHTO monthly average daily traffic and is designed to minimize DOW and monthly bias when data for less than 365 days per year are available. Computed monthly NALS values are averaged across all available years for each calendar month to remove potential bias in estimates toward partial years.
The challenge with this approach is that for classes that typically have low volumes, the NALS for individual months may not have the representative normalized shape that would have been computed based on cumulative annual axle load counts. In other words, certain load bins in monthly NALS would have zero values, and non-zero bins may have disproportionately high percentile values in individual monthly NALS. To mitigate this, a criterion of minimum cumulative number of 100 axles was used.
The following procedure shows the steps involved in computing RANALS using daily axle loading distributions from the LTAS DD_AX series of tables included in LTPP SDR24 (figure 33 is a flowchart that summarizes the flow of calculations):

Figure 33. Flowchart. RANALS computation.
Using this procedure, one set of RANALS was computed for each of the 26 SPS TPF sites. Each set of RANALS includes NALS for each vehicle class (classes 4 through 13) and each axle group type (single, tandem, tridem, and quad as applicable) representing expected axle loading distribution for a typical day of the year for a given site. Appendix D contains a CD with RANALS results for 26 SPS TPF sites.
The purpose of the global NALS defaults is to serve as an input to the MEPDG when little or no information about existing or expected future traffic loading patterns is available for a design site. Global NALS defaults were computed to follow the exact format of the original MEPDG defaults. In this way, any significant difference in default values can be implemented easily by MEPDG users.
This procedure is based on averaging RANALS from the SPS TPF sites that have sufficient data. The following procedure shows the steps involved in computing global NALS defaults (figure 34 is a flowchart that summarizes the flow of calculations):
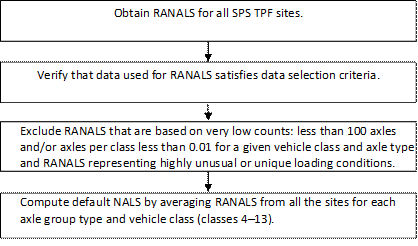
Figure 34. Flowchart. Global default NALS computation.
A supplemental set of NALS was developed to represent different loading conditions observed for different vehicle classes and axle group types among SPS TPF sites. These additional NALS were developed to provide flexibility to MEPDG users in the selection of axle loading defaults that best describe their local loading conditions. These NALS could be used to specify different truck loading conditions by class and axle group type. For example, a pavement designer may select a heavy axle load spectra for class 9 vehicles but a light load spectra for class 6 vehicles because those loading conditions are appropriate for the truck traffic using the roadway they are designing. These supplemental NALS expand traffic loading options for local calibrations of MEPDG models and for load sensitivity analyses.
To produce these supplemental NALS, specific attention was placed on identifying different axle loading conditions within each vehicle class and axle group type that are likely to produce significantly different MEPDG outcomes. The research team searched for a quantifiable approach that would take into account both the pavement damage potential of different axle load weights and the frequency of the application of those loads (i.e., the fraction of loads of a given magnitude in the axle load spectra) to compute a single statistic associated with each load spectra.
The approach selected was to convert load spectra into a single statistic that could be associated with pavement damaging potential per axle for each type of axle for each vehicle class (FHWA classes 4 through 13). The selected statistic RPPIF per axle was computed by multiplying theWij factors (see table 4) by the fraction of axles (of type j) in the normalized axle load spectrum within the same load bin i. That value was then summed across all load bins i included in that normalized axle load spectrum, computing a single RPPIF per axle for each axle group type j and each truck class. Using this method, each RANALS was converted to a single number for each type of axle by class of truck. Because Wij factors were developed based on outcomes from many different distress modes, these factors are not tied to any specific pavement distress but rather represent relative damaging potential across all types of distresses.
The intent of the RPPIF is to allow for simple summary comparisons of the size of different loading conditions. They are not intended for direct use as inputs to pavement analysis.
Using the RPPIF statistic, RANALS for individual SPS TPF sites were grouped for each vehicle class and axle group type so that each resulting group represented a loading condition with a high potential to cause a significant change in expected pavement life or design when that class of truck was heavily represented on a roadway compared to the other groups of sites representing different loading conditions for a given vehicle class and axle group type. These groupings were done separately for each class and axle group type.
The hierarchical clustering technique in the SPSS software package was used to group load spectra with similar damaging potential as defined by their RPPIF values. No specific number of clusters was preselected when performing this clustering process. Instead, the cluster process was run until just prior to the point where the mean RPPIF for two clusters was going to be larger than the RPPIF determined to be the minimum observed to cause a change in pavement depth of more than 0.5 inch. (Thus, if combining two current clusters to form one new cluster makes the maximum difference between the mean RPPIF for any two nearest neighbor clusters greater than the value shown in table 23, that new cluster is not formed and the cluster process stops.)
| Class | Frequency of Truck Occurrence (Percent of Total Truck Volume) |
Truck Type by Weight | Axle Group Type | |||
|---|---|---|---|---|---|---|
| Single | Tandem | Tridem | Quad | |||
| 7, 10, 13 | Infrequent (< 35 percent) | Heavy | > 0.55 | 0.41 | 0.49 | 0.8 |
| 6, 8, 11, 12 | Moderate to infrequent (< 50 percent) |
Moderate | 0.25 | 0.23 | N/A | N/A |
| 9, 4 | Frequent to moderate (> 50 percent) |
Heavy | > 0.13 | 0.09 | N/A | N/A |
| 5 | Frequent (> 75 percent) | Light | > 0.09 | N/A | N/A | N/A |
N/A = Not applicable.
These minimum RPPIF differences were determined from the MEPDG analyses presented in chapter 9 for vehicle classification scenarios representing the highest percentage of each class of vehicles found in the LTPP database. The values used to differentiate clusters are shown in table 23. By selecting the maximum observed percentage of each class of vehicles in the LTPP database, holding the other truck percentages and loads constant, it was possible to test the sensitivity of pavement design to changing loads of each class of vehicles.
If an agency were to develop its own State-specific load spectra clusters, it would have the option of using the values in table 23 to define when to stop the cluster process. However, an agency also could develop a State-specific version of table 23 by conducting the analyses similar to the ones described in chapter 9 using State-specific datasets. If this is done, the maximum observed percentage of any one class of truck or type of axle will change. The load spectra used to test MEPDG sensitivity will change as well, as only data from that State will be used. Because these key inputs change, State-specific break points between clusters will be different than in table 23. The outcome (the size in terms of allowable difference in mean RPPIF between clusters) will indicate which specific classes of vehicle and types of axles are important for pavement design in that State.
At the global level, this approach allowed for the adoption of fairly conservative values that account for the fact that some trucks are fairly uncommon and/or very light, and thus, nationwide, are less important to pavement design than other vehicle classes that are both heavy and numerous. This latter category of trucks (such as class 9 trucks) generally controls the design of the pavement. It is, therefore, important to more accurately estimate their axle loads. For truck classes that are rare (small in number relative to other truck types) or particularly light, it is less important to accurately estimate their axle loads, since even large errors in these estimates when multiplied by a small number of axles will have little impact on the final pavement design.
For the key vehicle classes that both have heavy axles and can be observed in large numbers (e.g., class 9 trucks), modest errors in estimated load/axle can result in significant errors in the pavement design. Thus, clusters for more important types of trucks (heavier trucks are more important because they cause more pavement damage) and classes of axle require clusters with small differences in mean RPPIF between the nearest neighbor clusters. At the same time, less common truck classes (e.g., class 12) and axle group types (e.g., class 7 quad axles) are allowed to have larger differences between nearest neighbor clusters, because these vehicle classes and/or axle group types contribute only a small percentage of the total load on specific pavements, and therefore even modestly large errors in their NALS are unlikely to result in significant errors in pavement design or expected pavement life.
Consequently, as can be seen in table 23, class 9 tandems, which are both common and are frequently heavy, must have clusters where the mean RPPIF of the resulting clusters are not more than 0.09 apart. Conversely, because tandem axles on class 13 trucks are generally not the type of axle which drives pavement design, neighboring clusters can be as much as much as 0.41 RPPIF different before clustering of class 13 tandems is halted.
Once clusters have been formed and default NALS computed for each load cluster, it is necessary to give users a means by which they can select between these different cluster groups. (Note: these default tables should only be used when better State- or site-specific load spectra are not available to the user.) These procedures are presented in chapter 10 of this report.
To develop default NALS representing different loading conditions, the following steps should be used (figure 35 is a flow chart that summarizes the flow of calculations):

Figure 35. Flowchart. Supplemental default NALS computation.
Each of these steps is described in the following subsections.
Step 1: Use Only Accurately Calibrated WIM Data
Calibrating WIM systems is a difficult, costly, and time consuming task. However, considerable LTPP research has shown that unless WIM calibration is performed carefully and routinely, the accuracy of WIM data tends to degrade quickly as a result of changes in WIM system performance caused by changes in roadway roughness and environmental conditions that affect performance of in-road sensors.(16) Poor calibration of WIM systems, combined with the effects of dynamic truck motion on the forces applied by truck axles on WIM scales or in-road sensors, can easily result in substantial error in the weights reported for truck axles. Calibration errors consequently result in very poor estimates of the number of heavy and very heavy axle loads being experienced by a pavement. These estimates result in poor traffic loading estimates.
Consequently, it is vitally important that an agency developing its own set of default load spectra only use data that have been collected by well-calibrated, accurately operating WIM scales. In addition, to assure that collected data reflect loading trends observed throughout the year, this computation requires a minimum of 12 months (each calendar month) of WIM data for which at least 7 days (each DOW) of load counts are available for each month to mitigate potential seasonal and DOW biases in loading estimates.
Step 2: Develop RANALS for Each Site
Computing NALS requires that each site being used in the computation have at least 24 h of valid data for each DOW for each month of a year. Procedures to compute RANALS were presented earlier in this section. These normalized load spectra can be used directly within the MEPDG and DARWin-METM procedures. They can also be grouped to create additional default or surrogate loading conditions. The best approach for grouping more than one site together is to convert each load spectra into an RPPIF statistic and then perform a cluster analysis based on similarities in RPPIF or other similar statistic.
Step 3: Compute RPPIF Statistics Using RANALS
To compute the RPPIF statistics needed to cluster the various load spectra, start with the RANALS (by class of vehicle and type of axle) from the previous step. Multiply load frequency corresponding to each load bin in those load spectra by the corresponding Wij factor from table 4. Sum these values across all load bins (i = 1 to n) for that load spectra as follows:
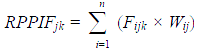
Figure 36. Equation. RPPIF statistic for vehicle class and axle type.
Where:
Fijk = Fraction of axles in load range i, for axle group type j, and vehicle class k.
Step 4: Determine the Importance of Specific Vehicle Classes and Axle Group Types
The next two steps are necessary if an agency wishes to cluster their site-specific NALS into groups and if they wish to incorporate into that grouping process State-specific truck travel attributes and pavement design considerations. These issues are discussed in considerable detail in the next chapter of this report.
The primary outcome of this task is to find traffic conditions (VCD and truck volume) that maximize the impact of each vehicle class on pavement design. That is, under what truck volume and VCD conditions does a given vehicle class represent the largest percentage of the total truck load on roads found in the State? Identified maximum truck volume conditions (relative to other truck volumes) can then be used to determine how sensitive the MEPDG outcomes are to the possible changes in load observed in that class.
These truck volume scenarios should be identified for each heavy truck type, resulting in up to 10 truck volume-by-class scenarios (for classes 4 through 13). These values are then used in the MEPDG sensitivity tests.
Step 5: Determine MEPDG Sensitivity to NALS
This task takes the data obtained in the previous steps and uses it to test the sensitivity of the MEPDG to the loading conditions present for each vehicle class scenario identified in the previous step. By holding all other loading conditions constant, except for the NALS for the selected vehicle class scenario, and then looking at the amount of pavement distress occurring due to the maximum volume of each truck type under different NALS loading conditions found in that State, it is possible to determine when specific loading conditions are important to the design process.
For example, class 5 trucks can be numerous. However, by looking at the loading conditions of class 5 trucks observed at SPS TPF sites, it is normally found that class 5 trucks always have light axles. As a result, regardless of which class 5 load spectra is used, even large numbers of class 5 trucks have little effect on pavement damage. As a result of these kinds of tests, it can be determined that it is not necessary to create multiple load spectra for class 5 trucks, as the selection between any rational group is unlikely to affect the MEPDG outcome. Consequently, only one group of loads is required for class 5.
Similarly, in a State where class 7 trucks are infrequently used (heavy natural resources may be carried in class 10 trucks in that State), the low volume of trucks (rather than the light weight of the truck) may mean that little benefit is gained from spending a large amount of resources on estimating class 7 weights. In such a case, only a very limited number of load spectra (e.g., moderate and heavy) may be warranted as defaults. Conversely, in a State where class 7 trucks are common and can be a moderately high percentage of the trucks on a roadway, the agency may find it necessary to create multiple class 7 loading groups to more accurately predict the effects of class 7 loads on pavement performance.
In addition to the observations described above, the sensitivity tests described in chapter 9 provide the quantitative outputs such as those shown in table 23 that are used in the cluster identification process. The outputs from the MEPDG are used to determine when two RANALS for a given vehicle class produce significantly different pavement analysis results. For example, a change in AC or PCC thickness of 0.5 inch could be used as one measure of significantly different. The difference in the RPPIF values between those two RANALS is used to establish criteria for determining when two RANALS should be kept as part of two different tier 2 NALS clusters. That is, if two RANALS produce significantly different pavement analysis outcomes, they are not similar, and they should not be combined into the same group for computation of default NALS. The difference in their RPPIF values then becomes a measure that can be used to determine the size of required boundaries between tier 2 NALS clusters, as shown in table 23.
Step 6: Perform Cluster Analysis
The final step in the development of default load spectra is the clustering of similar load spectra into a limited number of groups. This is best done with a statistical program such as SPSS®, SAS®, or similar programs. The cluster process used for this study was SPSS's hierarchical clustering option.
The clustering of RPPIFs computed in step 3 is controlled by the sensitivity of the pavement design process to traffic loadings (i.e., RPPIF differences identified in step 5). If State-specific sensitivity tests have been performed, use those results to control the clustering process. If no State-specific tests have been performed, use the values in table 23.
In the clustering process, the mean RPPIF between two nearest neighbor cluster should not exceed the values in table 23. Thus, the cluster process should be stopped one step prior to the step when that distance is exceeded.
Step 7: Compute NALS for Each Identified Loading Cluster
Once all clusters are identified, RANALS for the sites that belong to the same cluster should be averaged to compute default NALS representing that cluster group. This should be done for each vehicle class and axle type. For each computed average NALS, RPPIF and percent heavy statistics should be computed. Based on these statistics, a name and/or code should be assigned to the NALS cluster, similar to the names/codes included in the first column of Table 24.
| Axle Category by Weight | Average RPPIF per Cluster | Percent of Single Axles ≥ 15 kip | Percent of Tandem Axles ≥ 26 kip |
Percent of Tridem Axles ≥ 39 kip |
Percent of Quad Axles ≥ 54 kip |
|---|---|---|---|---|---|
| Very light (VL) | < 0.05 | < 3 | 0 | N/A | N/A |
| Light (L) | 0.05-0.15 | < 10 | < 10 | N/A | N/A |
| Moderate (M) | 0.15-0.30 | 10-30 | 10-30 | N/A | N/A |
| Heavy (H) | 0.30-0.50 | > 30 | 30-50 | < 50 | < 30 |
| Very heavy (VH) | > 0.50 | N/A | > 50 | > 50 | > 30 |
N/A = Not applicable.
If more than one cluster is identified for the same loading category, then sequential codes should be assigned to these NALS. For example, if two NALS cluster for class 9 tandems fall within the H loading category, cluster codes H1 and H2 should be used (H1 for the lighter of the two NALS and H2 for the heavier). A cluster that has a majority of sites for a given vehicle class and axle type should be selected as the default or typical cluster, and the letter code (T) should be added to the cluster code (e.g., H1(T)). All computed NALS should be saved to the database.
The MEPDG requires users to specify the number of axles per truck type as a part of traffic inputs for pavement design and analysis. These numbers are also called APC coefficients. These are used in the MEPDG procedure as a multiplier in the process of converting NALS to projected axle load spectra for pavement design.
APC coefficients are required for each vehicle class and axle group type. If a specific axle group type is not used for a given vehicle class, then a zero value is entered as the coefficient for that axle group type. One set of coefficients is used per pavement design, representing the typical number of axles observed per truck for each axle group type for vehicle classes 4 through 13.
APC statistics are computed for each vehicle class and axle group type by dividing the count of the number of axle load by type of axle by the count of vehicles of that class as collected for the same periods of time. Since the MEPDG requires only one set of APC coefficients per design, these values are computed based on the annual axle count and vehicle volume estimates.
The research team evaluated several approaches for developing the default APC based on WIM data collected for SPS TPF sites. While development of APC for classes and axle group types that are well represented was not affected by different approaches, axles per class for less represented truck and axle group types were found to be sensitive to different computation routines. A reason for that observation is that certain axle group types had occurrences only for some but not all days in a year. For these situations, estimated average APC were different based on assumption whether zero values should be used for the days where no axle group type occurrence was detected or these days should be excluded from the averaging process.
Averaging APC using only non-zero axle count days led to overestimation of the axle load application for underrepresented vehicle classes and axle group types because all the days with valid zero volume were excluded from computation of the average. Including days with zero axle counts led to very small values of APC coefficients for certain underrepresented axle group types. However, this latter approach was found to more accurately represent actual field conditions over the long design period. As a result, all the days with non-zero truck volume for a given vehicle class were included in computations. If no axles of a certain type were recorded for a given vehicle class and day but daily vehicle volume for this class was non-zero, then an APC coefficient of zero was computed for this axle group type and vehicle class.
The approach selected to compute default APC based on SPS TPF sites is as follows:
Average axle spacing or wheelbase information is used for MEPDG applications involving top-down slab cracking failure mode in JPCP. For this failure mode, the critical loading is caused by a combination of axles that place axle loads close to both ends of the same slab (in the direction of travel) at the same time. For JPCP designs with 15-foot-long slabs, axle spacing between 12 and 15 ft would result in axle loading positions most critical to development of top-down slab cracking. For JPCP with 20-ft joint spacing, the most critical joint spacing would be between 17 and 20 ft.
The current MEPDG top-down slab cracking model assumes that the majority of axle spacing that could induce top-down slab cracking is attributed to the wheelbase of the tractor unit in tractor-semitrailer combination trucks (FHWA classes 8 through 13). To account for such axle spacing, the MEPDG directly considers wheelbase of the tractor unit in the form of three inputs: percentages of tractor units with short, medium, and long wheelbase. The MEPDG indicates that the percentages of trucks in short, medium and long categories should be based on the axle spacing distribution (or wheelbase) of truck tractors in class 8 and higher. The MEPDG recommends the following three axle spacing or tractor wheelbase categories for analysis:
By default, the MEPDG software assumes an even distribution of short, medium, and long axle spacing occurrences (33, 33, and 34 percent, respectively).
In addition, the MEPDG states that if other vehicles in the traffic stream also have the axle spacing in the range of the short, medium, and long spacing defined above, the frequency of those vehicles could be added to the axle spacing distribution of truck tractors.(1) For example, if 10 percent of truck traffic is from multiple trailers (class 11 and higher) that have the trailer-to-trailer axle spacing in the short range, 10 percent should be added to the percent truck tractors for short axles. Thus, the sum of percent trucks in the short, medium, and long categories can be greater than 100.
A sample of axle spacing data from SPS TPF WIM sites was used to estimate percentages of axle spacing that fall in different length categories. The results of axle spacing distribution analysis could provide additional insights into what vehicle classes are likely to have axle spacing that could contribute to development of top-down cracking in JPCP.
The analysis was based on a sample of per-vehicle records for 1 month of individual vehicle records for each of SPS PFS WIM. The 1 month limit was used to manage millions of records. This sample size was determined to be a representative based on evaluation of the consistency of the axle spacing measurements through the year using analysis of the axle spacing for tandem axle groups (axles 2 and 3) of the two most common truck classes. For the majority of the sites, the month picked for a sample was June 2009. Where the measurements were not consistent, a different year was picked (2008), and data were evaluated for consistency. Where the volumes were low or data were not available, a different month was used. A total of 4.7 million records of axle spacing were analyzed.
The procedure to compute average axle spacing and wheelbase is as follows:
In addition, MEPDG states that if other vehicles in the traffic stream also have axle spacing in the range of the short, medium, and long spacing defined above, the frequency of those vehicles could be added to the axle-spacing distribution of truck tractors.(1) For example, if 10 percent of truck traffic is from multiple trailers (class 11 and higher) that have the trailer-to-trailer axle spacing in the short range, 10 percent should be added to the percent truck tractors for short axles. Thus, the sum of percent trucks in the short, medium, and long categories can be greater than 100. Short spacing should not include multi-axle groups like tandem, tridem, and quad in computation.
Axle spacing for multi-axle groups is the distance between the two consecutive axles of a tandem, tridem, or quad axle configuration (currently, the DARWin-METM software does not accept load spectra for axle group types with five or more axles for routine pavement design). Default axle spacing values can be computed based on averaging the values extracted from PVR records for all the sites using the following procedure: