Federal Highway Administration Design Manual: Deep Mixing for Embankment and Foundation Support

CHAPTER 6. DESIGN RECOMMENDATIONS

This chapter provides recommendations for designing deep mixing to support embankments and structures in transportation applications. These recommendations do not address all the factors that should be considered when designing deep mixing for other applications, such as stabilizing dam foundations. For support of transportation embankments, the recommendations in section 6.1 include detailed, step-by-step analysis and design procedures. Additional considerations that apply when DMM is used to support structures are described in section 6.2. Section 6.3 discusses the use of DMM to mitigate liquefaction potential, and section 6.4 provides comments about the use of DMM for excavation support. The procedures described in this chapter are for use by experienced geotechnical engineers. Consequently, being familiar with common geotechnical terminology and possessing the ability to perform earth pressure calculations, bearing capacity analyses, and slope stability calculations are prerequisites.

6.1 DESIGN OF DEEP MIXING TO SUPPORT EMBANKMENTS

Deep mixing for support of embankments is designed using allowable stress design methodology. Recommended steps in the design process are as follows:

1. Establish project requirements.
2. Establish representative subsurface conditions.
3. Establish trial deep mixed ground property values.
4. Establish trial deep mixed geometry including (1) general layout and definitions,
   (2) the center replacement ratio, and (3) the shear wall zone replacement ratio.
5. Evaluate settlement.
6. Evaluate stability, including slope stability, combined overturning and bearing capacity, crushing of the deep mixed shear walls at the outside toe, shearing on vertical plans in the deep mixed shear walls, and extrusion of soil between the deep mixed shear walls.
7. Prepare plans and specifications.

For unusually complex or critical projects, consideration should be given to supplementing the procedures with numerical analyses (e.g., Filz et al).⁽³⁴⁾

The following subsections describe the seven steps and provide the references that form the basis for the design procedure.

6.1.1 Step 1—Establish Project Requirements

In step 1, the project requirements are established, including the following:

• Embankment geometry (alignment, height, crest width, and side slopes).
• Traffic surcharge loading.
• Performance criteria (factor of safety values and allowable settlement).

Several factors of safety values are required in steps 4.2 and 6. Table 11 lists typical design values of safety factors for transportation embankments supported on DMM columns. By iterative analyses, values of the shear strength and geometry of the deep mixed material should be selected such that the calculated factor of safety values equal or exceed the design values.

Table 11. Typical design values of safety factors for design of deep mixing to support embankments.

It is recommended that Spencer's method be used to calculate F_s values because it satisfies all conditions of equilibrium and results in more realistic factor of safety values than some of the more simplified methods of slope stability analysis .⁽⁸⁷⁾ The design value of F_s in table 11 is based on using Spencer's method for the slope stability calculations. The analysis methods for the other failure modes listed in the table incorporate conservative assumptions. Consequently, lower design values of factor of safety are recommended for these failure modes.

An engineer may deviate from the recommended design values of factor of safety in table 11. For example, if subsurface conditions are well known, soil parameter values are selected conservatively, and the facility performance is not critical, then lower design values than those listed in table 11 can be considered. Conversely, if subsurface conditions are not well known, soil parameter values are not selected conservatively, or the facility performance is especially critical, then higher design values than those listed in table 11 can be considered. An experienced geotechnical engineer should make the selection of the design factor of safety for each of the failure modes and should justify the selection based on project-specific considerations.

6.1.2 Step 2—Establish Representative Subsurface Conditions

In step 2, the engineer establishes the soil material property values to be used in geotechnical analysis and design, including stratigraphy, groundwater conditions, and foundation material property values, as discussed in chapter 4. For the settlement calculations described in step 5, values of the compression ratio, recompression ratio, and preconsolidation pressure are necessary for the soils underlying the deep mixed zone. For the stability analyses described in step 6, end-of-construction conditions are typically critical, so undrained shear strength parameters would be used for saturated clays, and drained strength parameters would be used for permeable sands and gravels.

6.1.3 Step 3—Establish Trial Deep Mixed Ground Property Values

In step 3, the engineer establishes trial property values for the deep mixed ground and for the composite deep mixed zone for use in the analyses described in steps 4.2 and 6. Background information about property values for deep mixed ground is provided in chapter 5, and the necessary property values for design are established in this section. The design value for the shear strength of the deep mixed ground (s_dm) is estimated from the unconfined compressive strength to be specified (q_dm,spec), considering f_c and differences between unconfined peak and confined large-strain strengths (f_r). Factor f_v is also discussed and subsequently applied as appropriate to the analysis of each failure mode that involves the strength of the deep mixed ground.

A trial value of the 28-day q_dm,spec is assumed based on the background information provided in chapter 5. Typical values of q_dm,spec range from about 75 to 150 psi (0.52 to 1.03 MPa) for soft ground conditions. The necessary property values for design are established as follows:

1. Determine f_c in figure 30 using the estimated time (t) between mixing and application of 75 percent of the proposed embankment height. The values in figure 30 are based on a conservative interpretation of a wide range of data including cement and cement-slag blends with fine- and coarse-grained soil.⁽³⁴⁾ Site-specific testing could be used to justify larger values of f_c. One exception to the conservative trend provided by figure 30 is for highly organic soils or peat treated with 100 percent PCC, for which the value of f_c should be limited to 1.0 unless site-specific testing permits a higher value. However, cement-slag blends with a high proportion of slag are often used for organic soils and peat; in which case, figure 30 provides a conservative estimate of strength gain with time.

   Figure 30 can be used from 28 to 365 days between mixing and application of 75 percent of the proposed embankment height. The f_c value ranges from 1.00 for 28 days to 1.48 for 365 days.

2. Determine s_dm according to figure 33.

   
   Figure 33. Equation. Shear strength of the deep mixed ground.

   Values of f_r typically range from 0.65 to 0.9, and a value of f_r equal to 0.8 is recommended for application to transportation embankments.

3. Determine f_v from table 12. Factor f_v accounts for the greater variability that typically exists in the strength of deep mixed ground compared to the variability that typically exists in the strength of deposited clay soils. Since f_v depends on the design factor of safety value, the value of f_v should be determined for each unique value of design safety factor used in the analyses described in steps 4.2 and 6.

   Table 12. Values of f_v.

   Design Factor of Safety	Coefficient of Variation of the Deep Mixed Strength	fv
   		pdm = 70 Percent	pdm = 80 Percent	pdm = 90 Percent
   1.2	0.4	0.93	1.05	1.25
   	0.5	0.88	1.02	1.26
   	0.6	0.83	0.99	1.27
   1.3	0.4	0.89	1.01	1.19
   	0.5	0.82	0.95	1.17
   	0.6	0.75	0.90	1.15
   1.4	0.4	0.85	0.97	1.14
   	0.5	0.76	0.89	1.09
   	0.6	0.69	0.82	1.05
   1.5	0.4	0.82	0.93	1.10
   	0.5	0.72	0.83	1.03
   	0.6	0.63	0.75	0.96
   1.6	0.4	0.79	0.90	1.06
   	0.5	0.68	0.79	0.97
   	0.6	0.58	0.69	0.89

   p_dm = Probability that the actual deep mixed strength exceeds the specified deep mixed strength.
   Note: Values of f_v larger than 1.0 are possible even though the coefficient of variation of the deep mixed strength is larger than the coefficient of variation of the soil strength because p_dm is larger than the design strength of the untreated soil.⁽⁷⁴⁾

   The value of f_v depends on the following:

   • The coefficient of variation of the deep mixed strength, V_dm. With good QC, a DMM contractor should be able to achieve a V_dm value that does not exceed 0.50.
   • The probability that the actual deep mixed strength exceeds the specified deep mixed strength, p_dm. An appropriate value of p_dm depends on how tightly the specification is written and applied. A p_dm value of at least 80 percent would be appropriate for a well-written and well-applied specification. A specification is considered well written if it includes sufficient requirements that the contractor appropriately controls and it documents the quality of the deep mixed ground. A well-applied specification indicates that the owner will assure the quality of the deep mixed ground by carefully reviewing the contractor's QC documentation and appropriately enforcing the contractor's adherence to the specification requirements based on a good understanding of deep mixing construction technologies and project-specific design objectives. Additional discussion about specifications and QC/QA activities are presented in chapters 9 and 12.
   • The coefficient of variation of the soil strength, V_s. A value of V_s equal to 0.25 was used to develop table 12.
   • The probability that the actual untreated soil strength exceeds the design strength of the untreated soil, p_s. The value of p_s depends on the degree of conservatism used to estimate soil property values. A value of p_s equal to 0.67 was used to develop table 12.
   • The design factor of safety value. According to table 11, typical design factors of safety values depend on the failure mode. Therefore, different values of f_v may be necessary for different failure modes.

   Engineers wishing to consider input values different from those used to develop table 12 are referred to Filz and Navin.⁽⁷⁴⁾

   It is recommended that a well-written and properly applied specification and a well-qualified DMM contractor should be used on all DMM projects. When this happens, values of f_v corresponding to the midrange of inputs listed in table 12 (p_dm = 80 percent and V_dm = 0.50) are reasonable. Higher values of f_v may be appropriate during the later phases of a multiphase project involving the same participants and conditions as QC/QA procedures become more reliable. Alternatively, if the engineer is concerned that QC/QA will not be well executed, lower values of f_v (corresponding to p_dm = 70 percent and/or V_dm = 0.60) can be considered.

4. Determine Young's modulus of the deep mixed ground, E_dm, according to figure 34 for wet mixing or figure 35 for dry mixing.

   
   Figure 34. Equation. Young's modulus of deep mixed ground for wet mixing.

   
   Figure 35. Equation. Young's modulus of deep mixed ground for dry mixing.

   Figure 34 and figure 35 are correlations for E₅₀ of the unconfined compressive strength. Estimating E₅₀ of the deep mixed ground is discussed in more detail in chapter 5.

5. The unit weights of the deep mixed zones are also necessary for stability analyses. For typical w:c of the slurry, VR, and area replacement ratios used for DMM support of embankments, a reasonable approximation is that the unit weight of the deep mixed zone is equal to γ_soil  prior to mixing. However, if wet mixing is used and if the area replacement ratio, w:c, and/or VR are unusually large, the average unit weight of the deep mixed zone can be significantly less than  prior to mixing. In this case, phase relationships can be used to calculate the average unit weight of the deep mixed zone, as discussed in section 5.8.

6.1.4 Step 4—Establish Trial Deep Mixed Geometry

In step 4, the engineer establishes a trial geometry of deep mixing to support the embankment. Step 4.1 discusses the general layout of the embankment and deep mixed zone and defines the geometric parameters. A procedure for establishing the minimum area replacement ratio beneath the central portion of the embankment is discussed in step 4.2, and a procedure for estimating the minimum area replacement ratio beneath the side slopes of the embankment is discussed in step 4.3.

It is not necessary for the engineer to specify all of the geometric parameters defined in step 4.1. In fact, by determining and specifying only the minimum and/or maximum allowed values for certain geometric parameters, the engineer permits the DMM contractor flexibility in construction while still assuring that the final design will satisfy the requirements for settlement and stability.

Step 4.1—General Layout and Definitions

The overall dimensions and location of the deep mixed zone are generally selected to satisfy settlement and stability requirements, which are analyzed in steps 4.2, 5, and 6. Isolated columns and continuous shear walls are the most common configurations for transportation embankments. A cost effective combination uses isolated columns under the central portion of the embankment to control settlement and continuous shear walls oriented perpendicularly to the embankment centerline under the embankment side slopes to improve stability, as shown in figure 36.

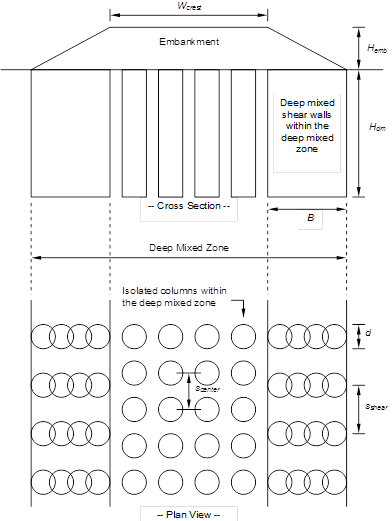
Figure 36. Illustration. Typical arrangement for deep-mixed zone beneath an embankment.

Where:
W_crest = Width of embankment crest.
H_emb = Height of embankment.
H_dm = Height of the deep mixed zone.
B = Length of the shear wall.
d = Column diameter.
s_center = Center-to-center spacing of isolated columns.
s_shear = Center-to-center spacing of shear walls.

The continuous shear walls can be constructed from overlapping columns or by using overlapping barrettes. Longitudinal walls can also be constructed to prevent ground extrusion between parallel shear walls, although this is not necessary unless the untreated soil between the shear walls is very soft and the spacing between shear walls is large. A method to calculate the factor of safety against extrusion is provided later in this chapter. The spacing between shear walls under the side slopes of the embankment does not need to be the same as the spacing between isolated columns under the central portion of the embankment.

The analysis and design procedures in this report are for the combination of isolated columns and shear walls shown in figure 36. Other configurations are also possible, but they may require other analysis and design procedures.

The area replacement ratio beneath the central portion of an embankment, a_s,center, is defined as the ratio of the column area to the tributary soil area surrounding the column. Where isolated columns are placed in a square array, as in figure 36, a_s,center can be calculated using the equation in figure 37. Typical values of a_s,center for deep mixing support of embankments range from about 0.2 to 0.4. The minimum value of a_s,center is established in step 4.2.

Figure 37. Equation. Area replacement ratio beneath the central portion of an embankment.

The geometry of overlapping columns used for shear walls under the side slopes of an embankment is shown in figure 38.

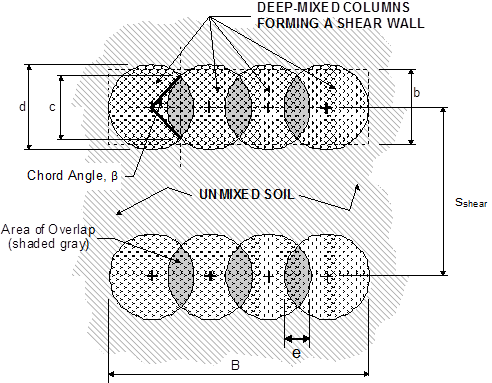
Figure 38. Illustration. Definition sketch for column overlap calculations.

Where:
e = Overlap distance.
β = Chord angle in radians.
c = Chord length.
b = Average shear wall width.

The area replacement ratio under the side slopes of the embankment, a_s,shear, is defined as the ratio of the area of the shear wall to the tributary soil area surrounding the shear wall. Where overlapping columns are arranged to create shear walls that are oriented perpendicularly to the embankment centerline, as in figure 36 and figure 38, a_s,shear is defined according to figure 39. Typical values of a_s,shear for deep mixing support of embankments are greater than or equal to a_s,center and range from about 0.2 to 0.4. The minimum value of a_s,shear is estimated in step 4.3.

Figure 39. Equation. Area replacement ratio under the side slopes of the embankment.

When the shear walls are constructed of overlapping columns, the extent of the overlap influences the minimum and average widths of the shear walls. The values of d, e, and s_shear can be used to calculate β , c, the overlap area ratio (ae), and a_s,shear, as shown in figure 40 through figure 43.

Figure 40. Equation. Chord angle expressed in radians.

Figure 41. Equation. Chord length.

Figure 42. Equation. Overlap area ratio.

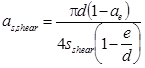
Figure 43. Equation. Area replacement ratio of the shear walls.

To illustrate the relationships in figure 40 through figure 43, values of β , c/d, and a_e are listed in table 13 for selected values of e/d. Typical values of e/d for shear walls beneath embankment side slopes range from about 0.2 to 0.35. Two important design parameters for embankment slope stability are the area replacement ratio for the shear walls, a_s,shear, which is provided by figure 43, and the ratio of the chord length to wall spacing, c/s_shear, which is obtained by dividing figure 41 by s_shear. Values of a_s,shear and c/s_shear are listed in table 14 and table 15, respectively, for selected values of e/d and d/s_shear. The value of a_s,shear is important for resistance to shearing through the deep mixed shear wall zone. The value of c is important for shearing on vertical planes in the deep mixed shear walls. Table 14 shows that a_s,shear is sensitive to d/s_shear, but it is not strongly dependent on e/d. Table 15 shows that c/s_shear is sensitive to both d/s_shear and e/d, especially for low values of e/d. Small column overlaps should be avoided in circumstances where shearing on vertical planes is an important design consideration.

Table 13. Values of β, c/d, and ae for selected values of e/d.

Table 14. Values of a_s,shear for selected values of e/d and d/s.

Table 15. Values of c/s_shear for selected values of e/d and d/s.

Step 4.2—Center Replacement Ratio

A trial value of a_s,center should be established based on the capacity of the isolated deep mixed columns beneath the central portion of the embankment using figure 44, with the value of f_v from table 12 corresponding to the design value of F_cc from table 11. Typical values of a_s,center for deep mixing support of embankments range from about 0.2 to 0.4.

Figure 44. Equation. Area replacement ratio beneath central portion of embankment.

Where q is the vertical stress from the embankment and surcharge.

Figure 44 is conservative because it assumes that the columns support the entire load from the embankment and surcharge without consideration of any support provided by the soil matrix.

Step 4.3—Shear Wall Zone Replacement Ratio

A minimum value of a_s,shear should be estimated. Typical values of a_s,shear for deep mixing support of embankments are greater than or equal to a_s,center and range from about 0.2 to 0.4.

The value of c/s_shear should be calculated using figure 40 and figure 45 based on the selected value of e/d, which is typically in the range from 0.2 to 0.35, and the estimated value of a_s,shear.

Figure 45. Equation. Ratio of chord length to shear wall spacing.

Table 16 summarizes the geometric parameters that an engineer should specify. Again, by specifying only the minimum and/or maximum allowed values for certain geometric parameters, the engineer is affording the contractor flexibility in construction while still assuring that the final design will satisfy the requirements for performance.

Table 16. Geometric parameters necessary for design.

6.1.5 Step 5—Evaluate Settlement

In this step, the post-construction settlement of the embankment is calculated as the sum of the compression of the deep mixed zone and the compression of the underlying ground. Differential compliance settlement between the base of the embankment and the top of the deep mixed zone is often assumed to occur during embankment construction prior to placing the pavement wearing surface. If the engineer judges that differential compliance settlement at the base of the embankment will be delayed, the procedures described by Filz and Smith can be applied to conservatively estimate this contribution to the total embankment settlement.⁽⁸⁸⁾ Compression of the deep mixed zone is calculated based on equal strains in the deep mixed ground and the adjacent untreated soil within the deep mixed zone underlying the central portion of the embankment. This approach is equivalent to using a composite modulus of the deep mixed ground and the adjacent soil. The composite modulus, M_comp, can be evaluated using figure 46.

Figure 46. Equation. Composite modulus.

Where M_soil is the constrained modulus of the untreated soil.
The implicit assumptions behind using E_dm and M_soil are that a stiff column is not significantly restrained from lateral expansion by the soft soil and that the overall system geometry provides lateral restraint for the soft soil in a unit cell. M_soil is the inverse of the compressibility, m_v, which is obtained from an oedometer test on the untreated soil over the stress range of interest.

Compression of the treated zone, ΔH_dm, can be calculated using figure 47.

Figure 47. Equation. Compression of the treated zone.

Compression of strata beneath columns installed by DMM can be computed using a load-spread method such as that employed for groups of driven piles.

If the calculated settlement exceeds the allowable settlement for a proposed embankment, then a_s,center, the column modulus, and/or the column length can be increased, depending on the primary source of the excess settlement.

When H_emb is at least two times the clear spacing between adjacent columns under the central portion of the embankment (i.e., H_emb ≥ 2(s_center - d)) and the embankment is constructed with typical good quality materials and procedures for placement and compaction, there is little risk of surface expression of differential settlements that occur at the base of the embankment, and special provisions for a load transfer platform at the base of the embankment are not necessary. When H_emb < 2(s_center - d), a load transfer platform can be designed using the procedures described by Sloan et al.⁽⁸⁹⁾ The load transfer platform should extend at least a distance s_center beyond the embankment crest beneath the embankment side slopes. If wet mixing is used, substantial spoils are produced at the ground surface, and the spoils can be used to construct all or part of the load transfer platform. The spoils should be placed and compacted as soon as they set up enough to support construction equipment, and the spoils will form a very strong embankment material.

On the embankment side slopes, there may be a potential for differential settlement of the embankment surface when H_emb becomes less than 2(s_shear - d). This could result in maintenance problems such as difficulty mowing. The concern for differential settlement above embankment side slopes is reduced if there is a firm layer of existing ground at the surface through which the deep mixed shear walls are installed. If differential settlement of the embankment surface at the slide slopes remains a concern, then additional settlement-control columns can be installed between the deep mixed shear walls or a load transfer platform can be designed using the procedures described by Sloan et al.⁽⁸⁹⁾ Spoils from wet mixing can be used in a load transfer platform under the embankment side slopes.

6.1.6 Step 6—Evaluate Stability

In this step, the trial geometry established in step 4 is analyzed for stability as follows:

• Procedures for analyzing slope stability are discussed in step 6.1.
• Procedures for analyzing combined overturning and bearing capacity are presented in step 6.2.
• Procedures for analyzing crushing of the shear walls at the outside toe of the walls are presented in step 6.3.
• Procedures for analyzing shearing on vertical planes in the deep mixed shear walls are presented in step 6.4.
• Procedures for analyzing extrusion of soft soil between the deep mixed shear walls are presented in step 6.5.

Step 6.1—Slope Stability

Slope stability analyses should be performed to determine the critical failure surface and corresponding factor of safety. Potential sliding surfaces may pass entirely beneath or entirely above the deep mixed shear walls, through the deep mixed shear walls, or partially through and partially below the deep mixed shear walls, as shown in figure 48. The composite shear strength of the deep mixed zones beneath the embankment, s_dm,wall and s_dm,center, should be assigned as indicated in the figure based on figure 49 and figure 50, with the value of f_v from table 12 corresponding to the design value of F_s from table 11. The resulting minimum factor of safety value from a comprehensive search for the critical failure surface is represented as F_s.

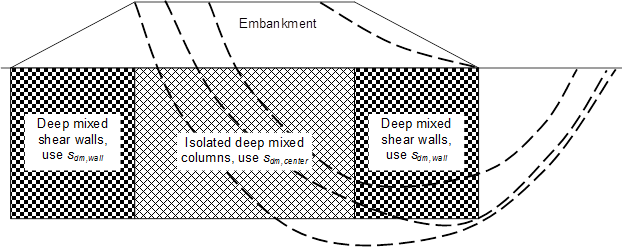
Figure 48. Illustration. Potential sliding surfaces and assignment of composite shear strength, s_dm,center and s_dm,wall.

Figure 49. Equation. Composite shear strength of the deep mixed zone beneath the shear walls.

1 lbf/ft² = 0.04788 kPa
Figure 50. Equation. Composite shear strength of the deep mixed zone beneath the central portion of the embankment.

Where s_soil is the shear strength of the soil through which the deep mixed columns are installed beneath the central portion of the embankment.

Figure 50 represents the isolated deep mixed elements as having a low shear strength value of 1,500 lbf/ft² (71.8 kPa). This is done to account for failure modes like column bending that can occur in isolated columns.

The calculated value of F_s should be compared to the design value from table 11. Careful slope stability analyses can be used to optimize the design as follows:

• If the value of F_s is too small and the critical failure surface passes beneath the deep mixed shear wall, then the geometry of the deep mixed shear wall zone should be changed to increase the value of F_s. Generally, this is accomplished by increasing the depth or width of the deep mixed shear wall zone. If the value of F_s is excessively large for this case, then a smaller deep mixed shear wall zone could be considered.
• If the value of F_s is too small and the critical failure surface passes through the deep mixed shear wall zone, then increases could be made to the strength of the deep mixed ground, the area replacement ratio, and/or the width of the deep mixed shear wall zone. When considering increasing the design strength of the deep mixed ground, limitations on practically achievable strengths should be carefully considered. If the value of F_s is excessively large for this case, then decreases could be made to the strength of the deep mixed ground, the area replacement ratio, and/or the width of the deep mixed zone.
• If the value of F_s is too small and the critical failure surface passes above the deep mixed shear wall zone, then the embankment slope could be flattened, a stronger embankment material could be used, and/or the embankment could be reinforced with geosynthetics. If geosynthetic reinforcement is used to address a critical failure surface above the deep mixed zone, then the stability analyses through or below the deep mixed shear wall zone should be repeated, and the resulting values of F_s should be compared to the required values.

Spencer's method is recommended for slope stability analyses because it satisfies all conditions of equilibrium and results in more realistic factor of safety values compared with some of the more simplified methods.⁽⁸⁷⁾ The minimum design value of F_s in table 11 is based on this recommendation. For typical project conditions, it is likely that a non-circular failure surface will be the critical surface. A careful search for the critical surface should be made using computer search and optimization routines by an experienced engineer. Critical slip surfaces should be checked for kinematic admissibility. Additional guidance for performing stability analyses is presented by Duncan and Wright.⁽⁹⁰⁾

Step 6.2—Combined Overturning and Bearing Capacity

Figure 51 provides a definition sketch that includes many of the symbols used in the step-by-step procedure for combined overturning and bearing capacity.

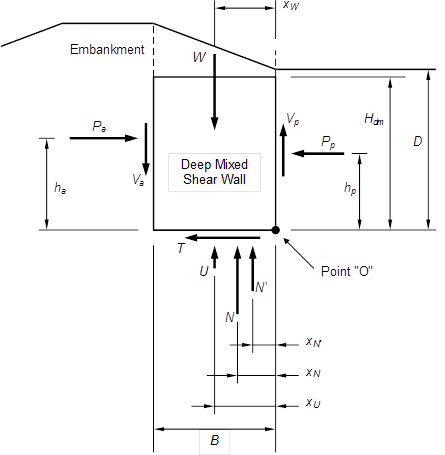
Figure 51. Illustration. Definition sketch for combined overturning and bearing calculations.

Where:
W = Total weight of the deep mixed zone and the overlying untreated soil and embankment material.
x_W = Horizontal distance from point “O” at the toe of the deep mixed zone to the line of action
of W.
B = Width of the deep mixed zone.
D = Depth to the base of the deep mixed zone at the toe of the slope.
P_a = Total active force, including the load from water pressures.
h_a = Vertical distance from point “O” to the line of action of Pa.
V_a = Vertical shear force on active side.
P_p = Total passive force, including the load from water pressures.
h_p = Vertical distance from point “O” to the line of action of Pp.
V_p = Vertical shear force on passive side.
N = Total vertical force acting upwards on the base of the deep mixed zone.
U = Vertical water force acting upwards on the base of the deep mixed zone.
N' = Effective vertical force acting upwards on the base of the deep mixed zone.
x_N = Horizontal distance from point “O” to N.
x_U = Horizontal distance from point “O” to U.
x_N' = Horizontal distance from point “O” to N'.
T = Horizontal shear force acting on the base of the deep mixed zone.

The following step-by-step procedure ensures that the design is sufficient to prevent combined overturning and bearing capacity failure of the deep mixed shear walls:

1. Select the design value of F_o based on table 11 and the accompanying discussion. The value of F_o will be used to factor down the strength of the soils that surround the deep mixed shear walls.
2. Determine mobilized shear strength parameter values for each layer of soil beside and beneath the deep mixed shear wall zone. If the shear strength of the soil layer under consideration is characterized by total normal stresses, use figure 52 and figure 53.

   
   Figure 52. Equation. Mobilized total stress cohesion intercept.

   
   Figure 53. Equation. Mobilized total stress friction angle.

   Where:
   c_m = Mobilized total stress cohesion intercept.
   c = Total stress cohesion intercept.
   Φ_m = Mobilized total stress friction angle.
   Φ = Total stress friction angle.

   If the shear strength of the soil layer under consideration is characterized by effective normal stresses, use figure 54 and figure 55.

   
   Figure 54. Equation. Mobilized effective stress cohesion intercept.

   
   Figure 55. Equation. Mobilized effective stress friction angle.

   Where:

   c'_m = Mobilized effective stress cohesion intercept.
   c' = Effective stress cohesion intercept.
   Φ'_m = Mobilized effective stress friction angle.
   Φ' = Effective stress friction angle.

3. Calculate values of P_a, h_a, V_a, P_p, h_p, and V_p using the mobilized strength parameter values from step 2. The lateral forces P_a and P_p are total lateral forces, including the effects of porewater pressures in soil layers whose shear strength is characterized by effective normal stresses. Porewater pressures are not separately considered for soils whose shear strength is characterized by total normal stresses. If water-filled tension cracks are possible, the water load should be included. The engineer is responsible for determining safe values of P_a, h_a, V_a, P_p, h_p, and V_p that reflect the project geometry, stratigraphy, material property values, and loading conditions. Several lateral force components may need to be included in the total force calculations depending on site conditions.
4. Determine the resultant vertical force, N, using figure 56.

   
   Figure 56. Equation. Vertical force.

   To calculate W and x_w, the unit weight of the deep mixed ground is often considered to be approximately unchanged from the unit weight of the untreated ground.

   If the strength of the soil beneath the deep mixed zone is characterized by effective normal stresses, then integrate the water pressures on the base of the deep mixed zone to obtain U and determine x_U. Calculate N' using figure 57.

   
   Figure 57. Equation. Effective vertical force.

5. Determine x_N using figure 58.

   
   Figure 58. Equation. Location of total resultant force.

   If the shear strength of the soil beneath the base of the deep mixed zone is characterized by effective normal stresses, then determine x_N' using figure 59.

   
   Figure 59. Equation. Location of the resultant force acting on the base of the deep mixed zone.

   If the calculated values of x_N or x_N' are less than or equal to zero, then the deep mixed zone may be too narrow. If the calculated values of x_N or x_N' are greater than half of B, then the deep mixed zone may be wider than necessary for overturning stability. If the values of x_N or x_N' are outside the range from zero to half of B, then the geometry of the deep mixed zone can be changed and the calculation process returns to step 2. However, if the minimum width B is fixed by project-specific constraints and x_N or x_N' is greater than half of B, then the design is safe against overturning and bearing capacity failure, and no further analysis of this failure mode needs to be done.

6. Calculate the bearing pressure at the toe of the deep mixed shear walls, q_toe. If the shear strength of the soil beneath the deep mixed shear walls is characterized by total normal stresses, use figure 60.

   
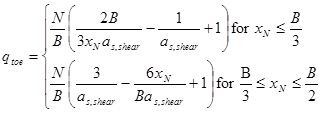
   Figure 60. Equation. Bearing pressure at the toe of the deep mixed shear walls using total normal stresses.

   If the shear strength of the soil beneath the deep mixed shear walls is characterized by effective normal stresses, use figure 61.

   
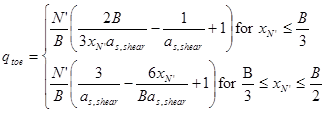
   Figure 61. Equation. Bearing pressure at the toe of the deep mixed shear walls using effective normal stresses.

   The expressions for q_toe in figure 60 and figure 61 are based on a linear pressure distribution, with stress concentration on the base of the shear walls having average width B, as shown in figure 38. The weight of the soil between the shear walls is assumed to be carried by the underlying soil.

7. Determine the allowable bearing pressure at the toe of the deep mixed shear walls, q_all. If the shear strength of the soil beneath the deep mixed shear walls is characterized by total normal stresses, use figure 62.

   
   Figure 62. Equation. Allowable bearing pressure at the toe of the deep mixed shear walls using total normal stresses.

   Where:

   N_c, N_γ, N_q = Bearing capacity factors obtained from Φ_m for the soil below the deep mixed shear walls using generally accepted sources for bearing capacity factors.
   γ_below = Total unit weight of the soil below the shear walls.
   γ_above = Average total unit weight of the soils above the base of the shear walls.
   b_min = Minimum allowable effective shear wall width, which can be estimated as 90 percent of the minimum allowable column diameter for typical values of e/d.

   If Φ_m equals zero, then N_γ = 0, N_q = 1, and N_c can be approximated as 7.5(1 + 0.1b_min/x_N) for b_min ≤ 2x_N. In this case, figure 62 reduces to figure 63.

   
   Figure 63. Equation. Allowable bearing pressure at the toe of the deep mixed shear walls using a total stress friction angle equal to zero.

   If the shear strength of the soil beneath the deep mixed shear walls is characterized by effective normal stresses, use figure 64.

   
   Figure 64. Equation. Allowable bearing pressure at the toe of the deep mixed shear walls using effective normal stresses.

   Where:

   N'_c, N'_γ, N'_q = Bearing capacity factors obtained from Φ'_m for the soil below the deep mixed shear walls using generally accepted sources for bearing capacity factors.
   γ_b,below = Buoyant unit weight of the soil below the shear walls.
   γ_b,above = Average buoyant unit weight of the soil above the base of the shear walls.

   The bearing capacity calculations can be performed using correction factors for shape, depth, and compressibility as appropriate.

   If q_toe is less than or equal to q_all, then the design is sufficient to prevent combined overturning and bearing capacity failure of the deep mixed shear walls. If q_toe is greater than q_all, then the geometry of the deep mixed zone can be changed to decrease q_toe and increase q_all. This would typically be accomplished by increasing the width or depth of the deep mixed zone.

   This procedure represents a potential failure condition for which the stabilized block overturns. This failure mode, which is not captured by ordinary limit equilibrium slope stability calculations, can control for tall and narrow deep mixed zones. By combining the overturning and bearing capacity calculations into a single calculation with the same factor of safety applied to the soils beside and below the deep mixed zone, ambiguities in the evaluation are avoided.

Step 6.3—Crushing of the Deep Mixed Shear Walls at the Outside Toe

In situations where the deep mixed ground overlies a hard bearing stratum, lateral loads could produce toe pressures that exceed the capacity of the deep mixed ground. The design factor F_c should be selected based on table 11.

If F_o is equal to F_c, then the intermediate values from step 6.2 can be used in the current step. If F_o is not equal to F_c, then steps 2-6 in step 6.2 should be repeated using F_c instead of F_o in figure 52 through figure 55. If the calculated values of x_N and x_N' are greater than half of B, then the design is safe against crushing at the toe of the shear walls, and no further evaluation of crushing is necessary. Otherwise, the values of q_toe (see figure 60 or figure 61) and Φ_m or Φ'_m (see figure 53 or figure 55) for the soil adjacent to the deep mixed ground at the toe of the deep mixed zone should be used in the following calculations.

The allowable capacity of the deep mixed ground can be determined based on the equation in figure 65, with the value of f_v from table 12 corresponding to the design value of F_c from table 11.

Figure 65. Equation. Allowable bearing capacity of the deep mixed ground against crushing of the deep mixed shear walls at the outside toe of the embankment.

Where σ_h is the lateral earth pressure at the toe.

A conservative value of σ_h is the at-rest lateral earth pressure. If the shear strength of the soil beneath the deep mixed ground is characterized by total normal stresses, then q_toe is determined from figure 60, and q_toe is the total vertical stress. In this case, the value σ_h to be used in figure 65 is given by the equation in figure 66.

Figure 66. Equation. Total lateral earth pressure.

Where:
K₀ = Effective stress at-rest lateral earth pressure coefficient determined based on Φ'_m for the soil adjacent to the deep mixed ground at the toe of the deep mixed zone.
σ'_v = Effective vertical stress in the soil adjacent to the deep mixed ground at the toe of the deep mixed zone.
u = Porewater pressure in the soil adjacent to the deep mixed ground at the toe of the deep
mixed zone.

If the shear strength of the soil beneath the deep mixed ground is characterized by effective normal stresses, then q_toe is determined from figure 61 and q_toe is an effective vertical stress. In this case, the effective lateral earth pressure, σ'_h, should be used in place of σ_h in figure 65, and σ'_h is given by the equation in figure 67.

Figure 67. Equation. Effective lateral earth pressure.

If q_toe is less than or equal to q_all, then the design is sufficient to prevent crushing of the deep mixed ground at the toe of the shear walls. If q_toe is greater than q_all, then the area replacement ratio, the width of the deep mixed zone, or the strength of the deep mixed ground should be increased.

Step 6.4—Shearing on Vertical Planes in the Deep Mixed Shear Walls

Shearing on vertical planes in the deep mixed shear walls is produced by eccentric loading corresponding to x_N < B/2. If the overlap between adjacent columns is insufficient, the shear walls can fail in a racking type of failure mode, as shown in figure 68. The design factor, F_v, should be selected based on table 11.

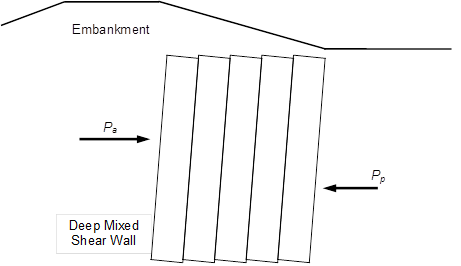
Figure 68. Illustration. Racking failure mode.

The following three-step procedure is used to determine whether the design is sufficient to prevent shearing on vertical planes in the deep mixed shear wall:

1. Determine the values of V_p, N, and x_N corresponding to F_v. If F_o or F_c is equal to F_v, then the resulting intermediate values can be used in this step. If this is not the case, then steps 2-5 in step 6.2 should be repeated using F_v instead of F_o in figure 53 through figure 55 to determine V_p, N, and x_N.
2. Compute the average vertical shear stress, τ_v, on the critical vertical plane in the deep mixed zone using figure 69.

   
   Figure 69. Equation. Average vertical shear stress.

3. Compute the allowable vertical shear stress, τ_v,all, in the deep mixed zone using figure 70, with the value of f_v from table 12 corresponding to the design value of F_v from table 11 .

   
   Figure 70. Equation. Allowable vertical shear stress.

   If τ_v is less than or equal to τ_v,all then the design is sufficient to prevent shearing on vertical planes in the deep mixed shear wall. If τ_v is greater than τ_v,all then measures can be taken to increase τ_v,all, such as increasing the strength of the deep mixed ground or the chord length at column overlaps or decreasing the shear wall spacing. Alternatively, measures can be taken to decrease τ_v, such as by increasing B. When considering increasing the design strength of the deep mixed ground, limitations on practically achievable strengths should be carefully considered.

Step 6.5—Extrusion of Soil Between the Deep Mixed Shear Walls

Extrusion of soft ground between shear walls could occur if the shear walls are widely spaced or short in the direction perpendicular to the embankment alignment. Extrusion between shear walls is not possible for sands or stiff clays under normal conditions, so only layers of soft clay need to be checked for this failure mode. The design factor, F_e, should be selected based on table 11 and the accompanying discussion.

The maximum clear spacing between shear walls, s_shear - d, should be limited based on the equation in figure 71 to prevent extrusion of soft clay.

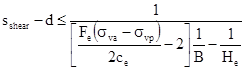
Figure 71. Equation. Maximum clear spacing between shear walls.

Where:
H_e= Thickness of a layer of soft clay to be analyzed for extrusion.
σ_va = Average value of the total vertical stress in the soft clay layer to be analyzed for extrusion immediately adjacent to the active earth pressure side of the deep mixed shear walls.
σ_vp = Average value of the total vertical stress in the soft clay layer to be analyzed for extrusion immediately adjacent to the passive earth pressure side of the deep mixed shear walls.
c_e = Average value of the total stress cohesion intercept in the soft clay layer to be analyzed
for extrusion.

This calculation should be repeated for different layers of soft clay soil to determine the critical value of s_shear - d.

If there is a project-specific reason to consider a larger value of clear spacing between shear walls than indicated by figure 71, then the shear wall length could be increased. Alternatively, a continuous wall of overlapping columns parallel to the embankment alignment and located within the zone of the deep mixed shear walls could be considered to prevent extrusion.

6.1.7 Step 7—Prepare Plans and Specifications

The final design resulting from steps 1-6 is incorporated in the project plans and specifications, as described in chapter 9.

6.1.8 Basis for Design Procedure

The analysis and design procedures in this section are based primarily on information provided by CDIT and with consideration of the findings of many other engineers and researchers. (See references 7, 9, 34-36, 46, 49, 56, 59, 61, 65, 68, 69, 78, 83, and 91-118.)

6.2 Design Considerations for DMM Supported Structures

Deep mixing can be used to support structures such as retaining walls, bridge abutments, and bridge piers. For support of structures, deep mixed columns should always be used in groups, and they should be designed to carry the entire load from the structure without consideration of any direct support to the structure provided by the soil between columns. Down drag from settlement of adjacent soil should be considered, if applicable.

The axial capacity of the deep mixed columns is the minimum of the structural capacity and the geotechnical capacity of the columns. The allowable axial structural capacity of a deep mixed column, q_all, can be determined according to figure 72, which incorporates a safety factor of 2.5 on s_dm, as determined from figure 33.

Figure 72. Equation. Allowable axial structural capacity of a deep mixed column.

The geotechnical capacity of a deep mixed column can be analyzed using procedures for drilled shafts because drilled shafts and deep mixed columns are similar in their effects on the soil between shafts or columns and in the degree of interlocking between the shaft or column and the adjacent soil.⁽¹¹⁹⁾ A safety factor of 3 is recommended to obtain an allowable geotechnical capacity from the ultimate geotechnical capacity.

Deep mixed columns are not normally used to resist lateral loads from structures. Settlement of structures on deep mixed foundations can be estimated using the same procedures described in section 6.1.5 for embankments, with the applied structure load converted to a pressure distributed over the area of the column group.

6.3 LIQUEFACTION MITIGATION

Deep mixing can be used to improve mass shear strength and contain liquefaction propagation.⁽⁹⁾ Walls of deep mixed columns are installed in grid arrangements to contain liquefiable soils, thus preventing a shear failure during a seismic event. An example plan view of soil-cement columns used on a BART system project is presented in figure 73.

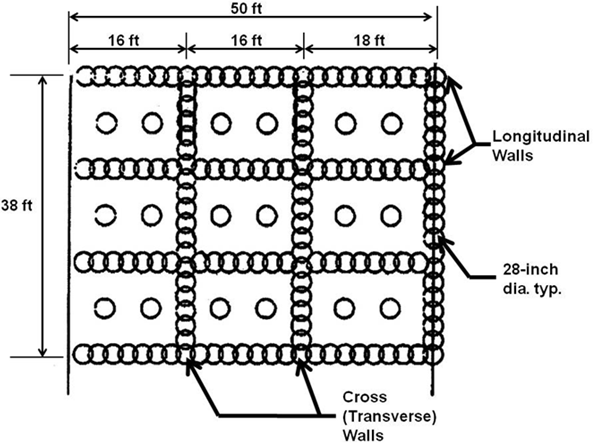
1 ft = 0.305 m
1 inch = 25.4 mm
Figure 73. Illustration. Plan view of soil-cement columns on BART project.⁽¹⁹⁾

A design procedure for liquefaction mitigation with DMM was developed in the National Deep Mixing Research Program. The design procedure and literature review are presented in Simplified Seismic Response Evaluation of Sites Improved by Deep Mixing.⁽⁴⁾

Deep mixing for liquefaction mitigation generally involves a rectangular grid or lattice pattern of columns with design dimensions of cell interior width (b), width or diameter of treatment (d), and length of treatment (L) specified to achieve a desired level of improvement, as illustrated in figure 74 and figure 75.

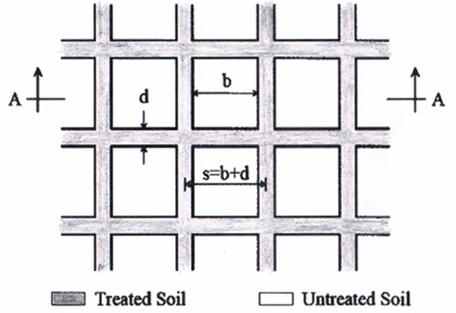
Figure 74. Illustration. DMM treatment plan.⁽⁴⁾

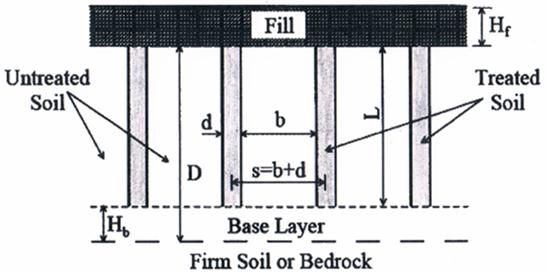
Figure 75. Illustration. Typical configuration of DMM for liquefaction mitigation.⁽⁴⁾

Where:

s = Center-to-center spacing of element walls.
D = Depth to first soil or bedrock.
H_b = Thickness of base layer.
H_f = Thickness of fill.

The seismic response characteristics of the DMM sites have been assessed based on the residual porewater pressure response (or liquefaction), which is a widely used engineering response indicator.

The steps proposed by Siddarthan and Suthahar to evaluate the residual porewater pressure response of DMM sites are summarized as follows:⁽⁴⁾

1. Evaluate soil response of DMM sites at various locations within and adjacent to DMM treated soil and in the free field for a variety of preselected test cases with different DMM treatments (configurations and properties), untreated soil conditions, and excitations. The result of this investigation is the establishment of a database of porewater pressure response ratios (PWPRs) normalized with respect to the free-field response. These PWPRs are computed at various depths along many vertical sections (within and adjacent to DMM columns).
2. Evaluate level ground seismic soil response in the free field in terms of porewater pressure at various depths using simplified liquefaction procedures outlined by Youd et al.⁽¹²⁰⁾ Unlike step 1, this is a site-specific analysis performed for a given untreated soil mass that is provided with DMM treatment. This step requires many input parameters such as soil layering and properties (e.g., thicknesses, SPT values, density, etc.) and excitation characteristics (e.g., acceleration strength and earthquake magnitude).
3. Establish PWPRs that are appropriate for the problem under consideration based on the case-specific untreated soil conditions, DMM treatment, and excitation characteristics from the database established in step 1. Multiply the free-field responses computed in step 2 by these equivalent factors to obtain the porewater response at various locations within and adjacent to the DMM columns.

The objective of this work was to produce simple design guidelines that practicing engineers can readily use to evaluate the effectiveness of various configurations of DMM treatments. The aforementioned seismic response evaluation model is simple and appropriately accounts for many important factors that affect the DMM treated soil response. More details on these steps are provided by Siddarthan and Suthahar.⁽⁴⁾

Other important seismic design issues, such as residual strength, permanent lateral deformation (e.g., lateral spread), and ground failure (e.g., sand boils), can be investigated based on the liquefaction analysis. The design issues can be assessed based on empirical relations that have been developed to specifically address each of these failure modes. Well-documented guidelines for these analyses are available and have been incorporated into design aids such as Special Publication No. 117 developed by the Division of Mines and Geology and the Southern California Earthquake Center.^(121,122)

6.4 Excavation support

For permanent excavation support, a bulkhead consisting of deep mixed shear walls can be designed using the procedures described in section 6.1 for embankments. In addition, one or more rows of overlapping columns should be provided along the bulkhead face perpendicular to the shear walls to prevent sloughing and raveling at the exposed face. The exposed face should be protected with shotcrete, precast concrete panels, or other protection to provide for long-term durability. Design of temporary excavation support is outside the scope of this report.