U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-15-034 Date: June 2015 |
Publication Number: FHWA-HRT-15-034 Date: June 2015 |
A total of sixteen different OGAs were tested in this study. From these series of tests, the strength parameters were found (table 11 through table 18). The strength of the aggregates was determined using three different devices: (1) SDS, (2) LSDS, and (3) LDTX. The choice of testing device plays a major role in the measured strength parameters.
To compare the testing devices, the measured friction angles were first investigated. Because the LDTX testing is performed saturated, the comparison focused on the LSDS test results under saturated conditions. Findings show that testing with the LSDS device produces higher measured friction angles than when compared with the LDTX device, regardless of the method of data interpretation, the MC or the ZDA approach (table 19 and table 20, respectively). In general, LSDS test results are generally between 8 and 52 percent higher than the LDTX test results. One exception is the No. 10 aggregate when using the MC approach; however, further study is needed to determine the reason for this smallest and most uniform aggregate tested.
Table 19. LSDS versus LDTX measured friction angles using MC approach.
MC Tangent Friction Angle |
LSDS Relationship to LDTX |
|||
|---|---|---|---|---|
Sample |
LSDS |
LDTX |
Total Difference |
Percent Difference |
No. 5 |
55.3 |
36.5 |
18.8 |
51.5 |
No. 56 |
54.4 |
39.5 |
14.9 |
37.7 |
No. 57 |
52.1 |
40.5 |
11.6 |
28.6 |
No. 6 |
57.5 |
36.4 |
21.1 |
58.0 |
No. 67 |
57.3 |
39.0 |
18.3 |
46.9 |
No. 68 |
48.7 |
38.1 |
10.6 |
27.8 |
No. 7 |
48.9 |
38.4 |
10.5 |
27.3 |
No. 78 |
44.9 |
34.9 |
10.0 |
28.7 |
No. 8A |
46.9 |
- |
- |
- |
No. 8B |
41.6 |
- |
- |
- |
No. 8C |
41.9 |
- |
- |
- |
No. 8D |
37.5 |
- |
- |
- |
No. 8E |
46.8 |
39.3 |
7.5 |
19.1 |
No. 89 |
41.2 |
38.3 |
2.9 |
7.6 |
No. 9 |
42.9 |
38.4 |
4.5 |
11.7 |
No. 10 |
37.1 |
40.1 |
-3.0 |
-7.5 |
LDTX = Large-diameter triaxial.
LSDS = Large-scale direct shear.
MC = Mohr-Coulomb
- = Not measured.
Table 20 . LSDS versus LDTX measured friction angles using ZDA approach.
ZDA CV Friction Angle (degree) |
LSDS Relationship to LDTX |
|||
|---|---|---|---|---|
Sample |
LSDS |
LDTX |
Total Difference |
Percent Difference |
No. 5 |
44.6 |
39.7 |
4.9 |
12.3 |
No. 56 |
52.9 |
39.4 |
13.5 |
34.3 |
No. 57 |
52.9 |
38.4 |
14.5 |
37.8 |
No. 6 |
51.7 |
36.8 |
14.9 |
40.5 |
No. 67 |
53.7 |
36.6 |
17.1 |
46.7 |
No. 68 |
47.9 |
38.7 |
9.2 |
23.8 |
No. 7 |
49.0 |
36.9 |
12.1 |
32.8 |
No. 78 |
45.5 |
38.3 |
7.2 |
18.8 |
No. 8A |
50.3 |
- |
- |
- |
No. 8B |
45.5 |
- |
- |
- |
No. 8C |
45.8 |
- |
- |
- |
No. 8D |
42.1 |
- |
- |
- |
No. 8E |
45.6 |
37.5 |
8.1 |
21.6 |
No. 89 |
45.8 |
40.3 |
5.5 |
13.6 |
No. 9 |
45.5 |
39.4 |
6.1 |
15.5 |
No. 10 |
42.0 |
34.8 |
7.2 |
20.7 |
LDTX = Large-diameter triaxial.
LSDS = Large-scale direct shear.
MC = Mohr-Coulomb
- = Not measured.
The mean size of the aggregate plays a role in the percent increase for LSDS test results as compared with LDTX test results (figure 40). As the aggregate gets larger, the percent difference typically increases. Overall, however, there is no observed relationship between friction angles measured using LDTX and LSDS testing for the range of OGAs tested (figure 41).
Looking at the range of aggregates tested, from the No. 5 to the No. 10, the mean tangent friction angle using the LSDS device under saturated conditions is 47.2 degrees, with a COV of 14.2 percent. The tests using the LDTX device, however, resulted in a mean tangent friction of 38.4 degrees and a COV of 4.6 percent. For the CV friction angle, the mean and COV using the LSDS device is 47.6 degrees, with a COV of about 7 percent; with the LDTX device, the values are 38.1 degrees and 4.2 percent, respectively. The aggregate type (i.e., size) had more of an impact with LSDS testing than with LDTX testing under loose compaction, likely as a result of the different boundaries conditions between the two tests.
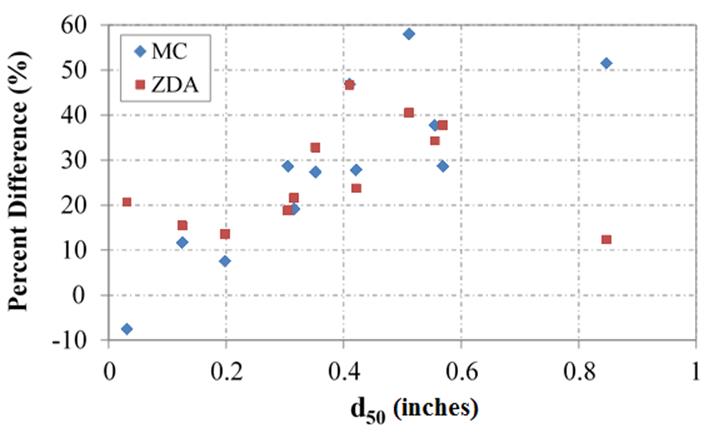
Figure 40. Chart. Difference between LSDS and LDTX as a function of mean aggregate size
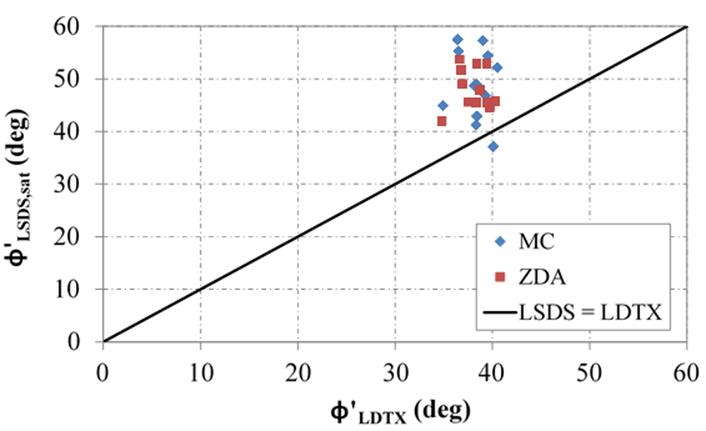
Figure 41. Chart. Relationship between LSDS and LDTX friction angles
A similar observation is made for the measured secant friction angles; however, the difference between LDTX and LSDS testing tends to decrease with increasing confining stress (figure 42). This observation again may be related to the reduced dilative behavior at higher confining stresses. The linear relationship found between the COV of the secant friction angles for a particular aggregate and the variation of the tangent friction angle from the average secant angle was found for both LSDS (figure 30) and LDTX testing (figure 39). The LDTX testing produces results that are considerably less scattered than the LSDS testing, thus reducing the variability across all samples tested.
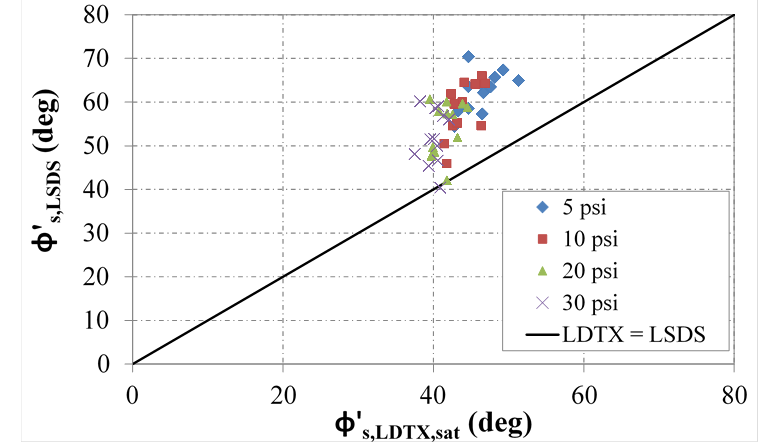
Figure 42. Chart. Relationship between LSDS and LDTX effective secant friction angles
When looking at the dilation angle, those measured with the LDTX device are also lower than those measured with the LSDS device (figure 43). This result is expected because of the forced failure plane that the aggregates must displace over in the LSDS device, causing more dilation. There is a general trend observed for dilation angles measured with the different large-scale devices; the dilation angle measured with LDTX is approximately 60 percent of that measured with LSDS. This result also explains the lower friction angles measured with LDTX because dilation behavior plays a big role in the strength of aggregates. Considering there is a trend with dilation but not with tangent or CV friction angles between LDTX and LSDS results, it is clear that more factors are contributing to the strength between the two test methods.
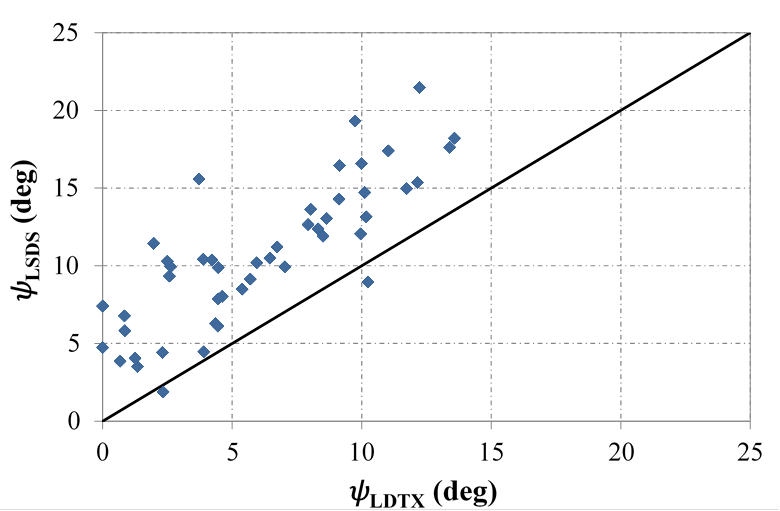
Figure 43. Chart. Relationship between LDTX and LSDS measured dilation angles
One parameter investigated in this study was scale of the direct shear testing device used to measure the strength of the aggregates. A 2.5-inch-diameter SDS device and a 12-inch-square LSDS device were used in the comparison. To ensure that the ASTM standard was met for each test, the samples were scalped prior to testing in the SDS device; no scalping was needed for the LSDS tests.(75) Tests were performed uncompacted under dry conditions.
Some samples measured with the LSDS results show higher strength than the SDS results; however, the differences largely lie within 10 to 20 percent (figure 44). The difference in the measured tangent friction angle when conducting SDS tests on scalped samples versus LSDS tests on complete samples ranged from 0 to 9.2 degrees when evaluating the results using the MC approach (table 21). When using the ZDA approach, the difference is greater, up to 14.5 degrees, and the LSDS results are about 40 percent higher than the SDS results (table 22).
The larger difference using the ZDA approach is explained by the variation and scatter in measured dilation angles between scalped and unscalped samples (see figure 22 and figure 27). The scalping process changes the dilation properties of the aggregates, with relative differences ranging from 15 to 65 percent; no trend was found (figure 45). The initial void ratio for testing is also changed, which has an impact on strength. Overall, scalped samples are unrepresentative of field behavior; results from strength testing cannot be relied upon.
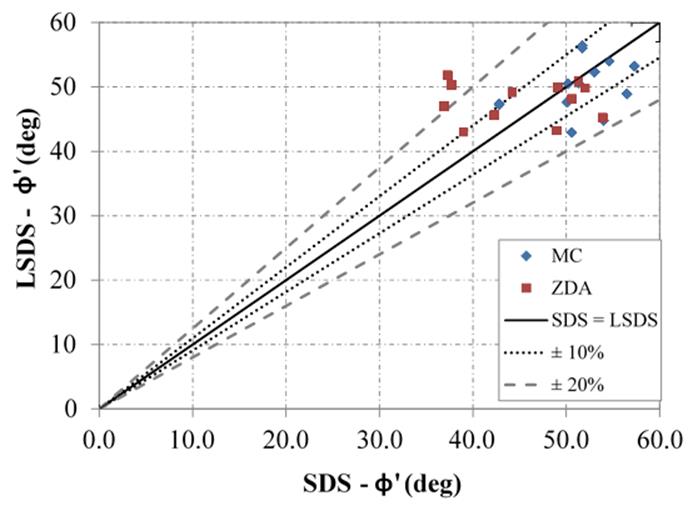
Figure 44. Chart. Relationship between LSDS and SDS measured friction angles
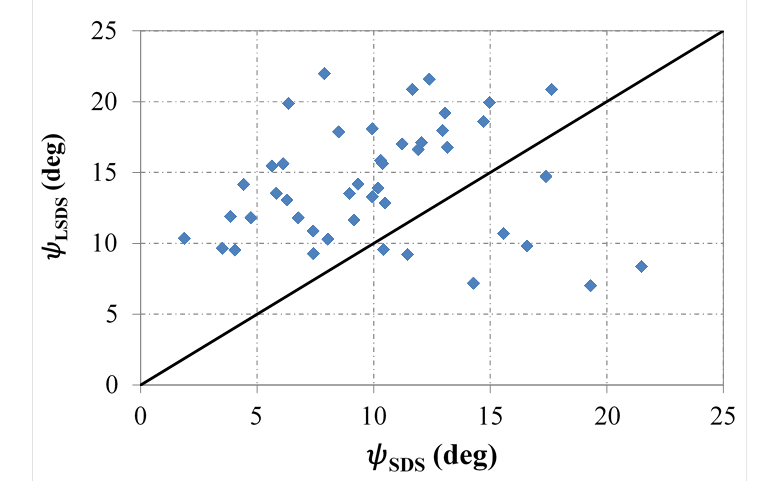
Figure 45. Chart. Relationship between LSDS and SDS measured dilation angles
Table 21 . SDS versus LSDS friction angles using MC approach.
AASHTO Gradation |
MC Friction Angle (degree) |
LSDS Relationship to SDS |
||
|---|---|---|---|---|
SDS |
LSDS |
Total Difference |
Percent Difference |
|
No. 5 |
50.1 |
47.6 |
-2.5 |
-5.0 |
No. 56 |
51.7 |
56.0 |
4.3 |
8.3 |
No. 57 |
56.5 |
48.9 |
-7.6 |
-13.5 |
No. 6 |
51.7 |
56.4 |
4.7 |
9.1 |
No. 67 |
57.3 |
53.2 |
-4.1 |
-7.2 |
No. 68 |
42.8 |
47.3 |
4.5 |
10.5 |
No. 7 |
54.6 |
54.0 |
-0.6 |
-1.1 |
No. 78 |
51.3 |
50.6 |
-0.7 |
-1.4 |
No. 8A |
53.0 |
52.3 |
-0.7 |
-1.3 |
No. 8B |
- |
43.4 |
- |
- |
No. 8C |
- |
48.3 |
- |
- |
No. 8D |
- |
37.8 |
- |
- |
No. 8E |
- |
52.2 |
- |
- |
No. 89 |
54.0 |
44.8 |
-9.2 |
-17.0 |
No. 9 |
50.2 |
50.5 |
0.3 |
0.6 |
No. 10 |
50.6 |
42.9 |
-7.7 |
-15.2 |
AASHTO = American Association of State Highway and Transportation Officials.
LSDS = Large-scale direct shear.
MC = Mohr-Coulomb.
SDS = Standard direct shear.
- = Not measured.
Table 22 . SDS versus LSDS friction angles using ZDA approach.
AASHTO Gradation |
ZDA Friction Angle (degree) |
LSDS Relationship to SDS |
||
|---|---|---|---|---|
SDS |
LSDS |
Total Difference |
Percent Difference |
|
No. 5 |
50.6 |
48.1 |
-2.5 |
-4.9 |
No. 56 |
37.7 |
50.3 |
12.6 |
33.4 |
No. 57 |
49.0 |
43.2 |
-5.8 |
-11.8 |
No. 6 |
53.9 |
45.2 |
-8.7 |
-16.1 |
No. 67 |
49.1 |
49.9 |
0.8 |
1.6 |
No. 68 |
36.9 |
47.0 |
10.1 |
27.4 |
No. 7 |
51.3 |
50.9 |
-0.4 |
-0.8 |
No. 78 |
44.2 |
49.2 |
5 |
11.3 |
No. 8A |
37.3 |
51.8 |
14.5 |
38.9 |
No. 8B |
- |
45.7 |
- |
- |
No. 8C |
- |
46.6 |
- |
- |
No. 8D |
- |
44.4 |
- |
- |
No. 8E |
- |
50.4 |
- |
- |
No. 89 |
42.3 |
45.6 |
3.3 |
7.8 |
No. 9 |
52.0 |
49.8 |
-2.2 |
-4.2 |
No. 10 |
39.0 |
43.0 |
4 |
10.3 |
AASHTO = American Association of State Highway and Transportation Officials.
LSDS = Large-scale direct shear.
SDS = Standard direct shear.
ZDA = Zero dilation angle.
- = Not measured.
The results of the Ottawa sand and the No. 10 aggregate tests can more directly be compared for scale effects because no or very little scalping was needed. The average secant friction angle from SDS testing of Ottawa sand at 5 psi was 32.2 degrees; from LSDS testing, it was 30.4 degrees. For the No. 10 aggregates, the difference is larger, up to 15.2 percent, with the SDS results also higher than the LSDS results. These findings are relatively consistent with research on sands in which larger devices resulted in lower measured friction angles for the same material.(54)
In contrast, the difference for the CV friction angles measured from SDS and LSDS tests is approximately 4 degrees, with the LSDS device producing a higher friction angle than that measured with the SDS device. This difference is considered negligible, however, because it is about 10 percent.(85) With dilation negated through the ZDA approach, it is expected that the aggregate would have similar strength regardless of the size of the device, assuming that all other aspects are constant.
The use of the traditional MC approach results in the peak, or secant, friction angle at each applied normal stress, which can provide the tangent friction angle over the range tested. The ZDA approach, however, results in the constant volume friction angle, which is a measure at the critical state. The tangent and constant volume friction angle are not equivalent parameters. A comparison between the friction angles resulting from the MC and ZDA approaches indicates that the difference between the two is within 20 percent regardless of testing device (figure 46).
The choice of data interpretation method, unless specified, will often default to the MC approach because it is the most common. The linear MC interpretation, however, results in measured cohesion for each test because the y-intercept of the best-fit approximation is not zero. This inconsistency for these cohesionless materials is attributed to the fact that the failure envelope is actually nonlinear; there is also aggregate interlocking and dilation that occurs during shearing, depending on the applied normal stress. In reality, the friction angle decreases with increased applied normal stress in a logarithmic function.
For the range of stresses tested, the secant friction angle corresponding to the peak for each applied normal stress was larger than that approximated from the MC approach. Because of these issues, an alternative ZDA method is proposed to determine the design friction angle. The ZDA approach reduces the friction angle to the critical state, thereby negating the effect of dilation from peak conditions. This approach helps reduce the amount of factors affecting the measured strength of aggregates and is theoretically the worst-case scenario.
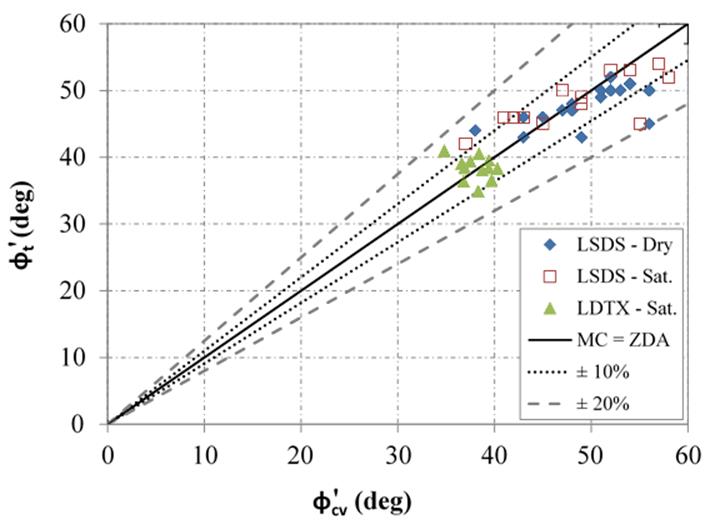
Figure 46. Chart. Relationship between measured tangent and CV friction angles.
Saturation was investigated in the LSDS device by performing tests under both dry and saturated conditions. Tests with saturation are considered drained tests because the material is free-draining, the water is free to move into and out of the sample, and the strain rate is relatively low to prevent build-up of pore pressures during testing. The measured friction angle results are shown in table 14 and table 15. Generally, for the samples larger than the No. 7 aggregates (dmax > 0.75 inches), the friction angles measured from the saturated tests using the MC approach were higher than from the dry tests, up to 15 percent (figure 47 ). The reverse trend was found for No. 7 and smaller aggregates (dmax ≤ 0.75 inches), where saturated testing produced lower friction angles. The biggest difference was for the No. 9 and No. 10 aggregates, where differences were up to 16 percent. Similar results are seen using the ZDA approach (figure 48 ).
For two-thirds of the aggregates (10 out of 15), the difference in measured tangent friction angles is within 10 percent. The results are similar for a larger population, almost 90 percent of the samples (13 out of 15), when using the ZDA approach. It is thought that saturation affects the dilative behavior, which is why the ZDA approach shows more negligible results. Overall, however, the difference between friction angles under dry and saturated conditions is within 20 percent for all samples regardless of test method (figure 49). While saturated tests take longer to perform than dry tests because of the time needed to achieve saturation and to drain the water after testing, the test should ideally mimic in-service conditions; however, the effect for OGAs appears to be minimal.
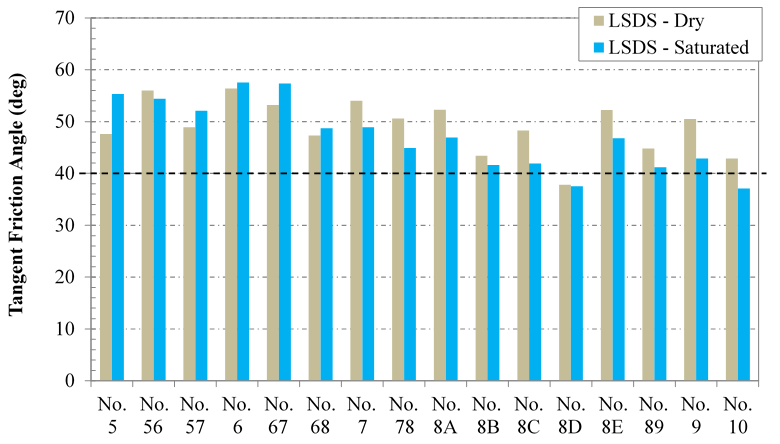
Figure 47. Chart. Measured friction angles under dry and saturated LSDS testing using the MC approach
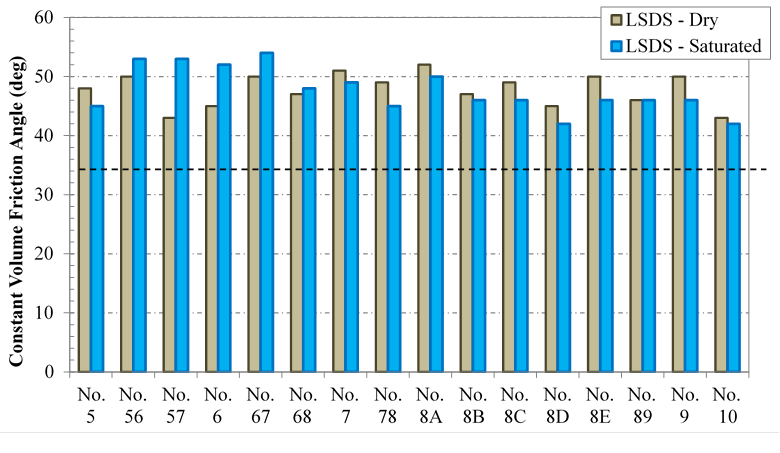
Figure 48. Chart. Measured friction angles under dry and saturated LSDS testing using the ZDA approach
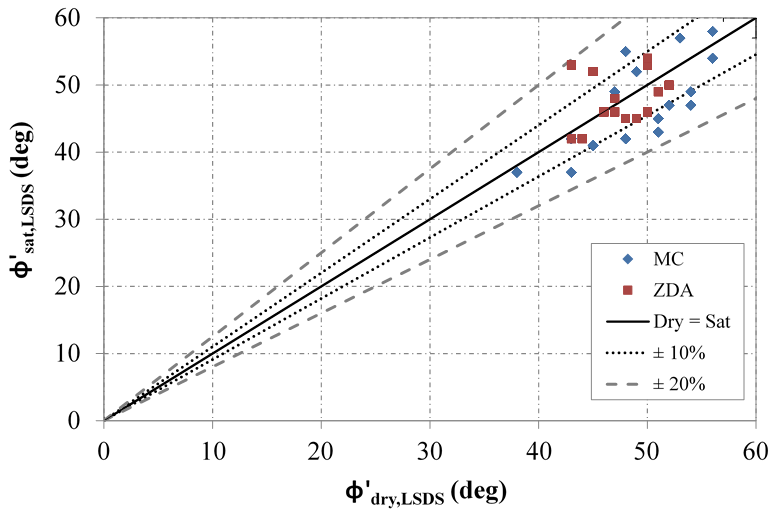
Figure 49. Chart. Relationship between measured friction angles under dry and saturated conditions in the LSDS device
In the absence of shear testing, designers will sometimes refer to correlations between other measured parameters and the friction angle of the material. The results were therefore compared with standard testing parameters to determine whether simple trends or correlations exist for OGAs.
It was found that when comparing the measured tangent and CV friction angles with the mean aggregate size (d50, see table 6), there is a general trend whereby as the mean size increases, the friction angle also increases under LSDS testing (figure 50 and figure 51, respectively). This result is not observed for LDTX testing in which the tangent friction angle is independent of mean aggregate size; however, when looking at the secant friction angles results from LDTX testing, a small positive relationship is observed that diminishes as confining stress increases (figure 52). This relationship may be the result of the low relative density under which testing occurred (about 30 percent). For the LSDS testing confined in a rigid box, the friction angle may not be affected as much for this reason as with LDTX testing, which has a more flexible boundary. Similar relationships are found with other gradation limits (e.g., d10, d30, d60, d85) and with the FM.
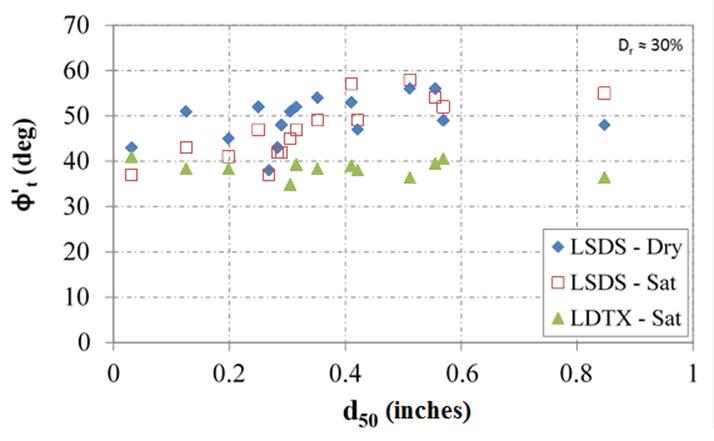
Figure 50. Chart. Relationship between tangent friction angle and median grain size
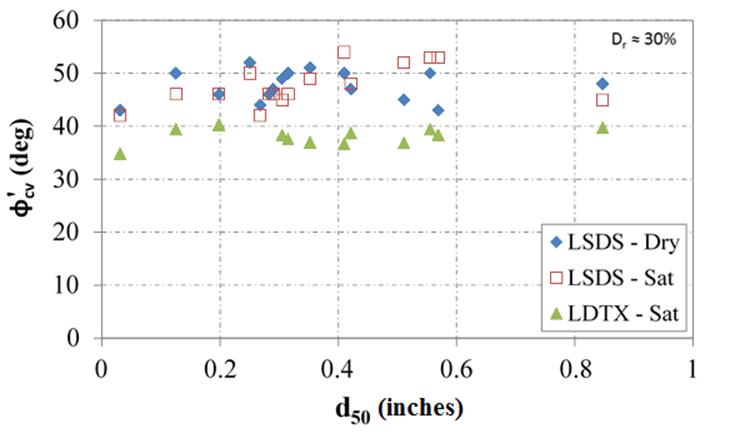
Figure 51. Chart. Relationship between CV friction angle and median grain size
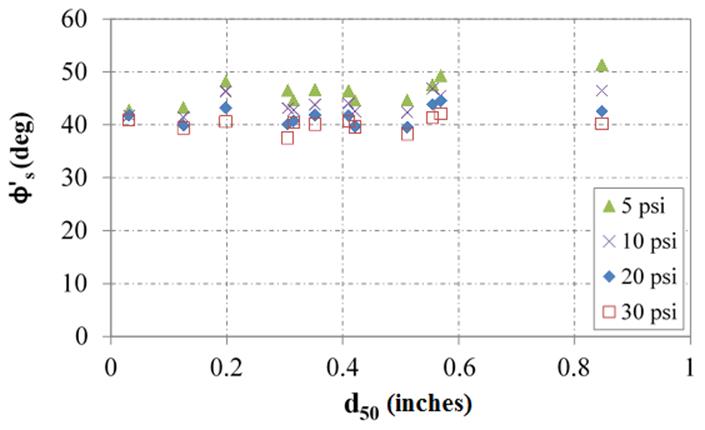
Figure 52. Chart. Relationship between secant friction angle and median grain size for LDTX testing
The coefficient of uniformity (Cu) is another important parameter; it helps describe whether a material is OG or well-graded. Based on the findings of this study, a clear relationship was not found between the measured friction angles and the Cu for the materials (figure 53 and figure 54). For OGAs, this lack of a relationship indicates that aggregate size plays more of a role than the overall gradation; however, the range of Cu values examined is relatively narrow.
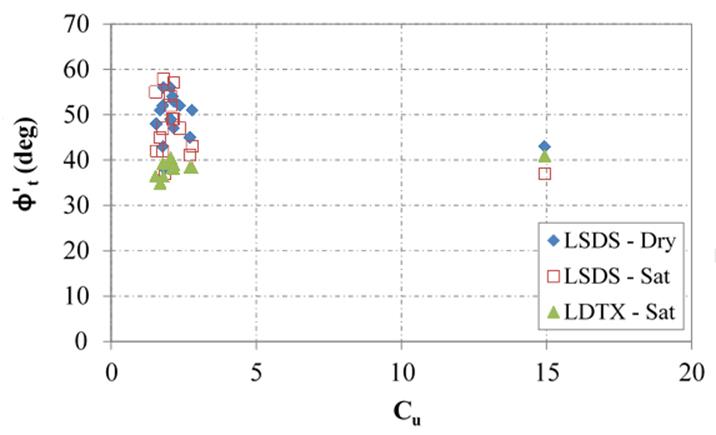
Figure 53. Chart. Relationship between tangent friction angle and Cu
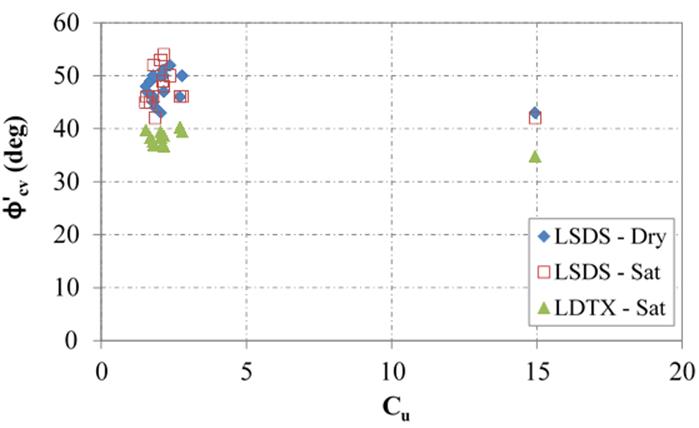
Figure 54. Chart. Relationship between CV friction angle and Cu
The samples were tested uncompacted at about 30 percent relative density, which was determined using the minimum and maximum unit weight of the OGAs found through vibratory table testing, described previously (table 7). By comparing the results for both LSDS and LDTX testing, it is found that the tangent friction angle is independent of the maximum density of the material (figure 55). A similar result is found when comparing the CV friction angle determined using LSDS testing and maximum unit weight (figure 56); however, there is a trend for the TX results whereby as maximum unit weight increases, the constant volume decreases.
These results are contrary to the Naval Facilities Engineering Command (NAVFAC) correlation that shows friction angle increasing with increasing dry unit weight for a given relative density.(86) Also contrary is that the estimated friction angle for a poorly graded gravel classified soil at 30 percent relative density is shown by NAVFAC as about 32 degrees, which is on the low side based on the measured test results in this study. More testing is needed on OGAs to investigate this discrepancy.
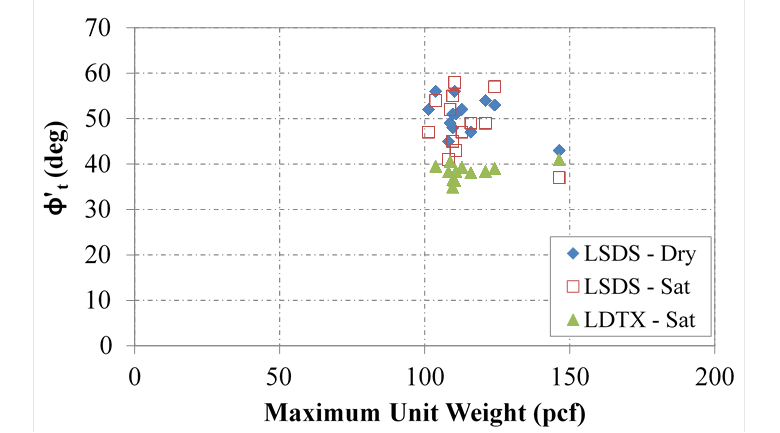
Figure 55. Chart. Relationship between tangent friction angle and maximum unit weight
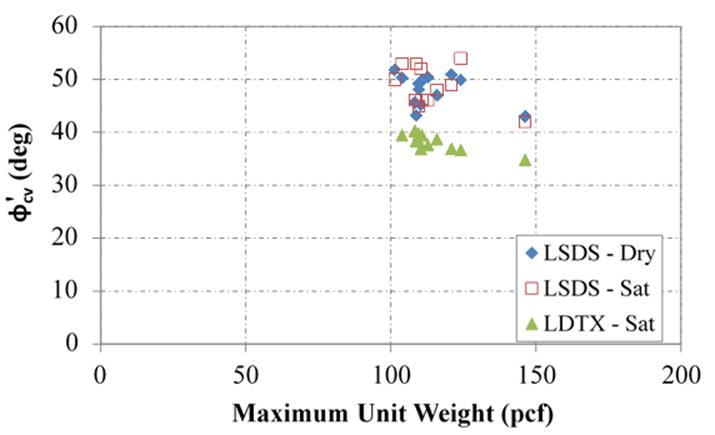
Figure 56. Chart. Relationship between CV friction angle and maximum unit weight
Others have postulated that the repose angle is equal to the constant volume friction angle; however, this theory is based on the behavior of soils.(10,87) For the OGAs tested, however, the CV friction angle is greater than the repose angle, with no clear relationship found between the measured repose angle and CV friction angle (figure 57).
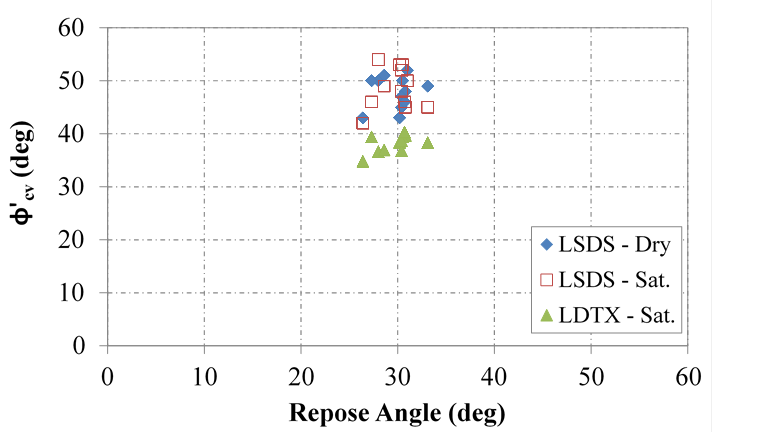
Figure 57. Chart. Relationship between CV friction angle and repose angle
Angularity, texture, and sphericity were all described in this study with AIMS2 (table 9). The tangent and CV friction angles measured with the LSDS device show an inverse relationship with the average angularity index (figure 58 and figure 59, respectively). While this result is contrary to expectations, it is postulated that as the aggregates get more angular, there is less contact area between the particles and a higher void ratio (i.e., less dense). Higher void ratios typically result in lower friction angles (figure 60).
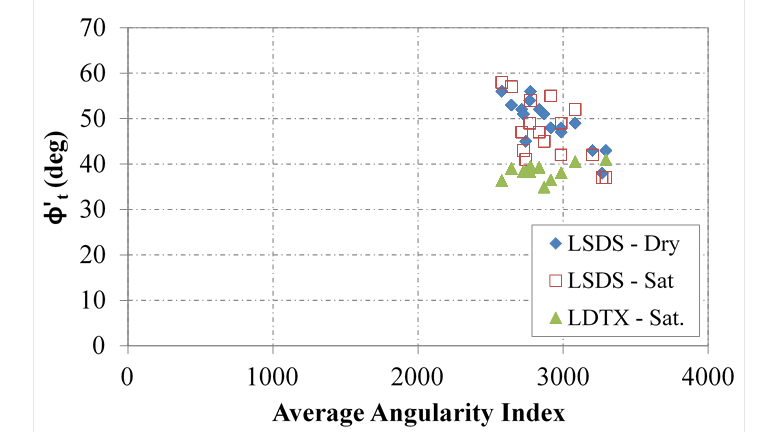
Figure 58. Chart. Relationship between tangent friction angle and angularity
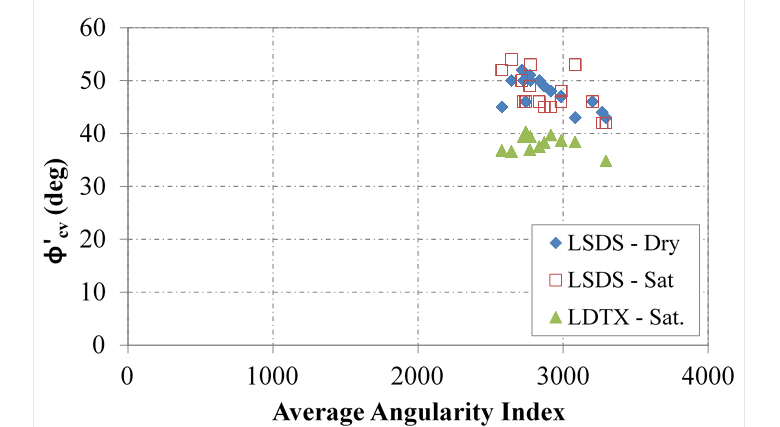
Figure 59. Chart. Relationship between CV friction angle and angularity
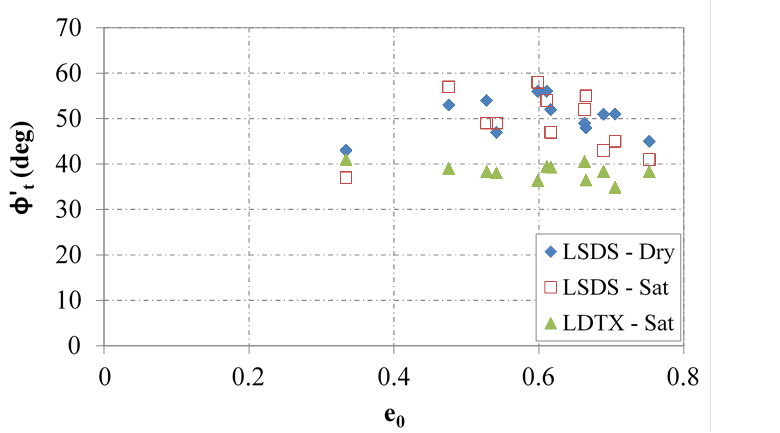
Figure 60. Relationship between initial void ratio and tangent friction angle
Because all of the aggregates have the same classification for angularity, however, it is difficult to make a definitive conclusion. Texture was found to not influence the measured tangent friction angle (figure 61) or the CV friction angle.
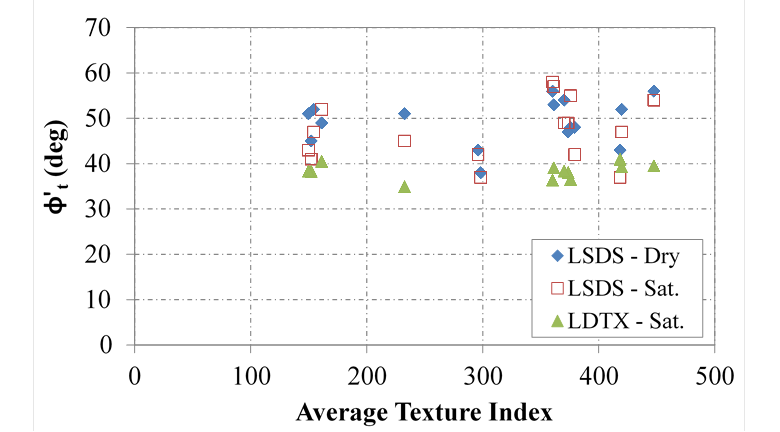
Figure 61. Chart. Relationship between CV friction angle and texture
Sphericity does play a role in LSDS test results; as the average sphericity index increases, the friction angle also increases (figure 62 and figure 63). As with many of the other parameters, the LDTX results are independent of the sphericity. With the forced failure plane in LSDS testing, sphericity (the general roundness of the aggregates) affects the amount of dilation that occurs. Assuming the same angularity, flat/elongated particles will more easily slide past one another than rounded particles.
The measured angularity indexes help explain the variation between the various No. 8 aggregates tested, regardless of data interpretation (figure 64 and figure 65). To a lesser extent, sphericity influences the results as well (figure 66). Additional testing is needed to expand the database and develop design equations to correlate angularity with friction angle for all relevant AASHTO OGAs.
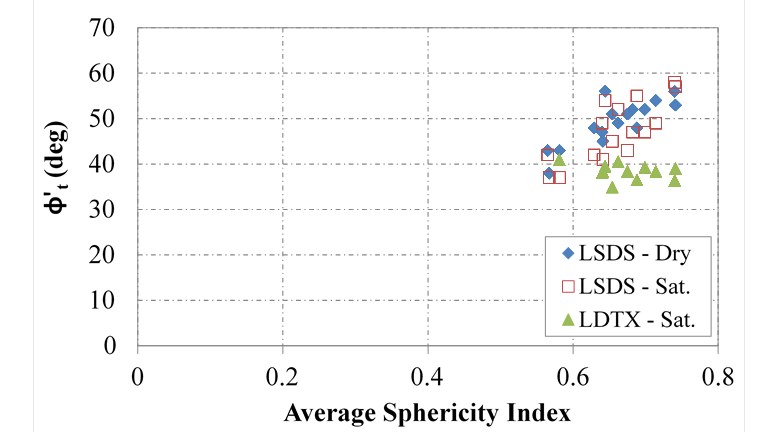
Figure 62. Chart. Relationship between tangent friction angle and sphericity
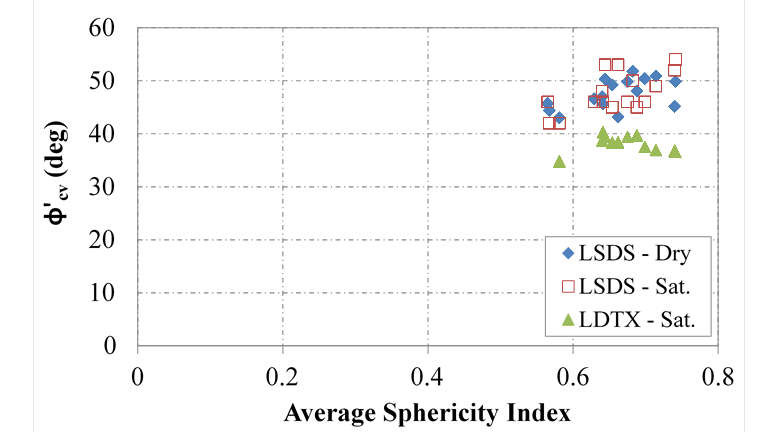
Figure 63. Chart. Relationship between CV friction angle and sphericity
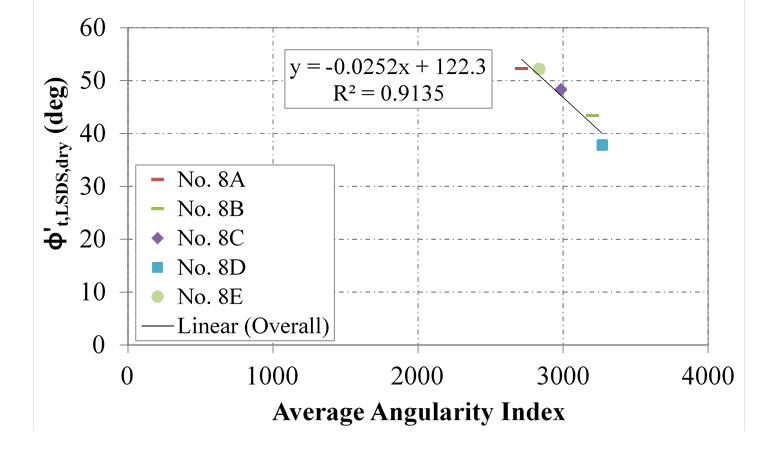
Figure 64. Chart. Relationship between tangent friction angle and angularity in LSDS testing for AASHTO No. 8 aggregates
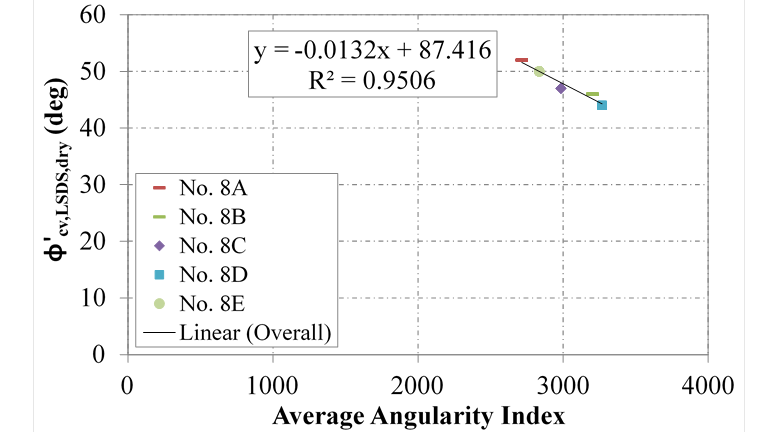
Figure 65. Chart. Relationship between CV friction angle and angularity in LSDS testing for AASHTO No. 8 aggregates
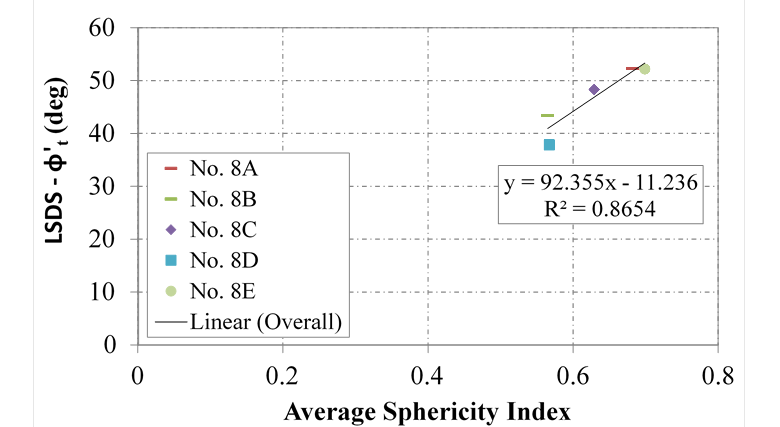
Figure 66. Chart. Relationship between tangent friction angle and sphericity in LSDS testing for AASHTO No. 8 aggregates