U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-16-045 Date: October 2016 |
Publication Number: FHWA-HRT-16-045 Date: October 2016 |
The fifth edition of Hydraulic Engineering Circular 18 (HEC-18) Evaluating Scour at Bridges introduced a new equation for pier scour in coarse bed materials.(1) The equation, shown in
figure 1, is based on work conducted by the Federal Highway Administration (FHWA) to develop more physics-based relations.(2)
![]()
Figure 1. Equation. Pier scour in coarse bed materials (HEC-18).
Where:
ys = Scour depth, ft (m).
y1 = Approach flow depth, ft (m).
a = Pier diameter, ft (m).
K1 = Correction factor for pier nose shape, dimensionless.
K2 = Correction factor for angle of attack of flow, dimensionless.
σ = Sediment gradation coefficient (D84/D50), dimensionless.
H = Hager number (densimetric particle Froude number (Fr)), dimensionless.
As prescribed in HEC-18, this equation is only applicable to clear water flow conditions and to what is described as coarse bed materials. Coarse bed materials are defined as those with D50 greater than or equal to 0.79 inches (20.1 mm) and a gradation coefficient greater than or equal to 1.5.
The Hager number used in the equation was developed by Oliveto and Hager and is defined in figure 2.(3,4)
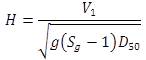
Figure 2. Equation. Hager number.
Where:
V1 = Approach velocity, ft/s (m/s).
D50 = Median grain size, ft (m).
Sg = Specific gravity of the sediment, dimensionless.
g = Gravitational acceleration, ft/s2 (m/s2).
The equation in figure 1 was provided to supplement the primary scour equation in HEC-18, which is shown in figure 3.
![]()
Figure 3. Equation. General pier scour equation in HEC-18.
Where:
K3 = Correction factor for bed condition, dimensionless.
Fr1 = Approach flow Fr, dimensionless.
The equation in figure 3 was modified from previous versions by dropping a coarse bed adjustment factor, K4, when the equation in figure 1 was introduced. Current guidance is to use the equation in figure 1 for conditions to which it is applicable and then to use the equation in figure 3 for most other conditions.
The objective of the research described in this report is to determine if the equation described in figure 1 can be used for conditions beyond those to which it is currently limited.