U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-17-109 Date: January 2018 |
Publication Number: FHWA-HRT-17-109 Date: January 2018 |
The primary means of evaluating capacity in this project was to tensile test strands and individual wires to failure. Then, residual capacity of strands and wires subjected to blast or thermal cutting was compared to that of virgin strands or virgin wires. This chapter describes the methods of conducting tension tests and the results of that testing.
The tension testing of strands was performed in accordance to ASTM A1061.(3) The analysis of results per ASTM A1061 was deviated from at times because ASTM A1061 is meant for testing a new strand, not a strand in a damaged condition. All testing was performed in a 220-kip[1] capacity, servo-valve hydraulic-controlled, four-post universal testing machine. The machine is equipped with hydraulic grips for clamping specimens. The lower grip of this machine is able to freely spin about the hydraulic cylinder’s axis, which is a detriment when testing a seven-wire strand. A seven-wire strand has six wires wrapped in a single direction around a central king wire, and when placed under tension, the outer wires will naturally untwist the strand. Therefore, the lower grip required modification to prevent free rotation and resist the torque the strand produces under tension. This is illustrated in figure 20 showing an overall view of the load frame. A steel angle that connects between two of the load frame’s posts crosses in front of the lower hydraulic grip. Behind the angle at its midpoint are two roller bearings spaced such that a rectangular block bolted to the grip is restrained to only move up and down within the bearings. This system reacts the torque generated by the strand through a force couple into the load frame posts.
Figure 21 shows a closeup view of the lower grip with the grip, wedges, and padding labeled. The wedges were a typical V-wedge used for gripping round products. The aluminum padding was used so the serrated teeth in the wedges did not gouge the strand itself and to ensure that strand was being gripped through friction only. This gripping method is one of three that are outlined in the ASTM A1061 specification.(3) The aluminum padding was an off-the-shelf extruded angle with dimensions of ¾- by ¾- by 1/8-inch thick. The desired grip pressure was determined to be 3,500 psi—less than this and the strands would slip; greater than this and the propensity of shear failures in the grip increased. This arrangement of wedge, padding, and grip pressure was refined via numerous trial tension tests and seemed to provide the most consistent results. While the method of gripping seemed to have been optimized, virgin strands always failed near one of the grips. As described in ASTM A1061, failures outside the gauge length should be ignored; however, they may be considered valid provided the strand meets the material specification (ASTM A416 in this case) and the fracture was a tensile failure. If the grip is influencing the test results, the fracture surface is oriented at 45°. This is referred to as a “shear failure,” and the results were generally ignored. This will be discussed more in the sections that follow.
Strain was measured with a video extensometer that worked on the principle of two-dimensional digital image correlation (DIC). DIC works by tracking the motion of a high-contrast pattern applied to the specimen with a digital video camera. In this case, the pattern comprised random dots applied with a white paint marker. This is shown in figure 21. The video extensometer could provide class B accuracy from the beginning of the test all the way through fracture. This is mentioned because ASTM A1061 assumes a class B extensometer is used up to the strand yield strength, and a lower accuracy class D extensometer is used post yield through fracture.(3) Likewise, the procedures used to calculate yield strength and elongation assume that the grips will have seating losses, and assumed strain values are used at set ratios of the minimum breaking strength. The use of hydraulic grips and the video extensometer negates some of the calculation assumptions of ASTM A1061, but for this project, ASTM A1061 calculations were strictly followed.(3)
Strands were cut to an approximate 36-inch length, and given the 5-inch depth of the wedges, this left approximately 26 inches from wedge face to wedge face. The wedge-to-wedge distance could not increase more than this, as the crosshead was positioned at its extent. This allowed for a 24-inch-gauge length over which the video extensometer could measure. The 24-inch-gauge length is the minimum allowed by ASTM A1061.(3) The specimens were loaded at a strain rate of 0.015/min over the 24-inch-gauge length. This equated to a crosshead displacement rate of 0.36 inch/min. Generally, failure would occur within a 5-min period.
Since the original strands were greased and sheathed, certain difficulties in testing were posed. The HDPE covering on the strand was easily removed with a utility knife; however, the grease was more problematic. It was found that a tension test could only be successfully run when the grease was completely removed from the strand. Once the strand was cut to length, a hose clamp was placed about 10 inches away from each end, and the six outer wires were untwisted away from the king wire, splaying them outward. Then, a pressure washer with conventional dish soap was used to blast away the grease and, once dried, pliers were used to twist the outer wires back into position around the king wire.
Virgin strands were used as a baseline to assess the level of damage to the bundles subjected to thermal cuts and blasts. The virgin strands were taken from other qualification tests not described in this report. These qualification tests all produced little to no visual damage within the middle 4 ft of the bundles where the specified procedures of each test were applied. Since the bundles were nominally 12 ft long for each qualification test, virgin strands were taken from the outer 4 ft of these bundles. Numerous strands were used as practice to ensure the testing machine and control software were working as expected and to refine the grip pressure and padding. Ultimately, 16 official virgin strand tension tests were used to define the baseline strength of the strands.
Of the 16 tests on virgin strands, 3 failed in shear within the grips. Figure 22 shows a typical shear failure of a wire from the virgin 2 specimen with the characteristic inclined fracture plane. Shear failures in or at the grips may artificially reduce the strength of the strands, and thus these results were not part of statistical calculations or plotted in any figures shown. The desired fracture pattern is a tension failure that is normal to the applied stress; figure 23 shows a tension failure of five wires in virgin 4, and the remaining two intact wires are noticeably necked.
All pertinent results for each test are reported in table 1. This table lists the modulus, yield load, strain at yield, actual ultimate tensile strength (AUTS), strain at AUTS, and elongation. The modulus was calculated as the best-fit slope between 20 and 65 percent of the maximum breaking strength. Yield load was calculated using the preload method described in the ASTM A1061 test specification.(3) Often, elongation values were less than the strain at AUTS because the method to calculate elongation in ASTM A1061 defines the zero strain level to be at 10 percent of the maximum breaking strength.
The results listed in table 1 show, on average, the virgin strand did meet the minimum requirements of ASTM A416.(2) The minimum yield and AUTS results were repeatable with coefficients of variation (COVs) less than 1 percent. Plots of load versus strain for the 13 valid virgin specimens are presented in figure 24. All plots nearly overlay each other and show a distinct bilinear behavior. However, elongation values varied much more with a COV nearing 10 percent. The variation of the elongation values is observable in figure 24 from the range of strains over which fracture occurred.
—Not a requirement.
aSpecimen failed to meet at least one ASTM A416 requirement.(2)
bCalculation of average and COV ignores specimens with shear failure in grips.
cRepresents a minimum value.
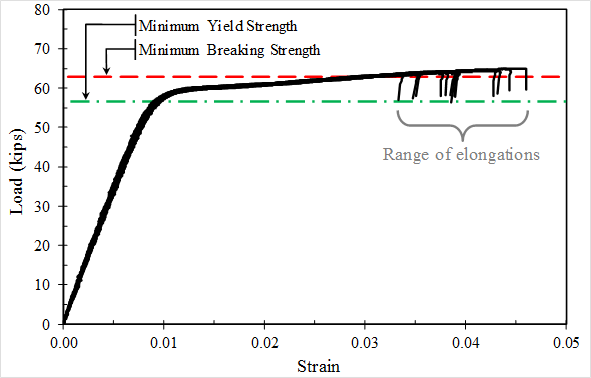
Source: FHWA.
Figure 24. Graph. Load versus strain for all virgin strands not exhibiting shear failure in grips.
Individual wires of strand were also tension tested to establish a baseline. Six additional, untested virgin strands were cut to approximately 33 inches in length and then were each separated into six outer wires and one king wire. The king wire has a slightly larger diameter (0.210 inch) than the six outer wires (0.202 inch). Therefore, a population of king and outer wires was tested to establish the baseline for each.
Wires were tested in a different servo-valve hydraulic-controlled load frame (from the one shown in figure 20); it also had hydraulic wedge grips but an overall lower force capacity. Wires had to be tested on this machine because it had wedges capable of gripping wire with a diameter that small. These wedges were only 4 inches deep (in contrast to 5 inches in the other machine), and the wire was directly gripped without padding. The same DIC system was used to measure strain over a 24-inch-gauge length so the results would commensurate with the virgin strand testing. The loading rate was specified as 0.36 inch/min, again, to commensurate with the strand testing.
The king wire and two randomly selected outer wires were tested from each strand. The results in terms of AUTS, strain at AUTS, and total elongation are presented in table 2 and table 3, respectively, for outer and king wires. Only results from wires that fractured within the gauge length are reported in the tables.
aUsed elongation at fracture criterion in ASTM E8, not the elongation criteria in ASTM A416.(2,4)
aUsed elongation at fracture criterion in ASTM E8, not the elongation criteria in ASTM A416.(2,4)
Plots of all the outer wire specimens are shown in figure 25 and for the king wires in figure 26. Because the outer wires have an initial helical shape, there is an initial low stiffness response at low load as the wire is straightened out. Because of this effect, each curve has been offset by a certain strain value such that the elastic portion of the curve intercepts the origin of the plot. This was also done with the king wires; however, since they were mostly straight to begin with, they did not demonstrate the same initial low stiffness behavior.
Strands were selected from a protected bundle subjected to two thermal lance qualification tests for residual capacity tension tests. The selected intact strands (no wires cut) were separated into two categories: One group represented strands assumed closest to the heat source (neighbor to strands completely cut by the tip of the penetrating thermal lance), and another group represented strands assumed to be farthest from the heat source. The decision to select strands for these two categorical groups was made by inspecting the location of the intact strands relative to the location of the strands with all seven wires cut as seen in figure 3 through figure 6. For example, in cut A, strand A30 neighbors three strands with all wires cut by the thermal lance (strands A29, A23, and A24). Thus, strand A30 is close to the heat source and survived with no wires cut. But perhaps the wires in strand A30 were affected by heat (the hypothesis to test). For the second categorical group, strand A43 is located as far as possible from the same heat source as strand A30, with no wires cut and hypothetically less heat exposure. The results from the residual capacity tension tests are reported separately for cuts A and B.
Depending on the thermal cycle applied to strands, microstructural changes might have occurred in the steel wires. These microstructural changes could affect the residual tensile strength in the steel wires. The thermal lance qualification tests did not employ thermocouples to measure magnitude or duration of temperature. However, prior to conducting the tension tests, a visual inspection of the strand (relative to other strands) might provide a qualitative measure of the maximum temperature reached in a steel wire. All strands were originally greased and sheathed, and it is recognized that these coatings will change under sufficiently high heat. The HDPE cover on the majority of the strands selected from the thermal lance test groups was melted. It was also noticed that the grease was either partially or completely burned away from some of the selected strands. Figure 27 shows a picture of the untested B23 strand, considered representative, which shows the HDPE has burned away for a few inches, and the dull appearance at the center of the strand indicates that the grease was possibly burned away on the outer wires. The shinier appearance near the melted HDPE indicates intact grease on the outer wires. After the strands were tested in tension, it was easier to observe the condition of the HDPE and grease both on the outer six wires and around the king wire. Using the information describing the condition of the HDPE and grease might help provide a qualitative measure of the temperature the strand may have experienced.
Data from the tensile test results from thermal lance cuts A and B are listed in table 4. The table presents the same mechanical data as listed for the results of virgin strand tension tests in table 1. Additional columns are provided to denote how many wires fractured, the location of the fractures, and the condition of the HDPE and grease. The condition of the HDPE was either melted or not. The grease could have three condition states: completely burned away, burned away only on the outer wires, or not burned at all.
—No data to report.
aTwo wires were nicked by the reciprocating saw blade while dismantling the bundle. Fracture did not initiate near saw nicks.
bOne wire was nicked by the thermal lance. Fracture did not initiate near thermal lance nick.
cTwo wires were nicked by the thermal lance. Fracture initiated at each nick.
dShear failure in grip.
eSlipped in grip and never failed.
fOne wire was nicked by the reciprocating saw blade while dismantling the bundle. Fracture initiated at saw-cut nick.
gNo evidence of thermal lance nicks, though fracture in one wire initiated at slag ball fused to a wire.
hVideo showed slipping at grip, and first fracture was a shear failure of the king wire.
iCalculated by dividing AUTS by 64.14 kip, the average AUTS of virgin strands.
Table 4 footnotes add important commentary to explain posttest observations not known a priori. First, according to the map of damaged wires presented in figure 4, the only strand with seven wires intact with damage was A35; this strand was originally documented as having one wire damaged. Visual examination of the fractured strand after testing (shown in figure 28) clearly shows that fractures on two wires initiated from nicks on each wire from the thermal lance. This indicates that the damage mapping presented in figure 3 through figure 6 is subject to some error, as melted HDPE and/or burned grease may have masked damage to wires, though this damage became more apparent after pressure washing to remove grease before testing. Similarly, strand A34 had no reportable damage, but posttest inspection did reveal one nick on a wire. Note, also, that during the dismantling of the bundle, wires in strands A32 and A43 received nicks from the reciprocating saw blade during the cutting operation to remove the melted HDPE cover. The nicks on wires in strand A32 did not appear to affect the residual capacity test results. However, the nicks on wires in strand A43 did appear to affect the residual capacity test results. A posttest view after the tension test on strand B12 is shown in figure 29, and no obvious nicks are visible around the fracture. However, a slag ball fused to one wire coincided with a fracture in one wire, but since two other wires simultaneously fractured, the low strength was likely the result of microstructural changes due to excessive heat, not necessarily the fused slag ball.
Statistical measures of the data are not presented in table 4 because the data are subject to the influence of varied heat conditions not readily assessed. Plots of the load versus strain of all the tested thermal lance strands without shear failures are presented in figure 30 and figure 31, respectively, for strands farthest and closest to the heat source. Examining figure 30 for strands farthest from the heat source (A37, A40, A41, A42, B25, B31, B38, and B41) shows curves that follow the reference curve of virgin strands with little deviation. The data from only these eight strands result in an average AUTS of 63.5 kip and 3.4 percent elongation; the average results from the virgin strand were 64.1 kip and 3.8 percent elongation. A null hypothesis test considering the two means to be equal was conducted using a Wilcoxon rank-sum test. The hypothesis was acceptable at the two-tailed 0.01 significance level but rejectable at the two-tailed 0.05 significance level. It was concluded from this that the average virgin results were not statistically different from the average results from the eight strands farthest from the heat.
The results of load versus strain for 13 strands closest to the heat source (i.e., adjacent to strands that were cut or damaged) are presented in figure 31. The results for 4 of 11 strands (A36, B19, B24, and B28) align with load versus strain curves for a virgin strand. Therefore, the proximity of a strand to the thermal cut is not a direct indicator of strength reduction. The HDPE cover of all four of these strands was melted, but the grease was intact around the king wire. The lowest residual capacities were observed after the tension tests of strands exhibiting a form of obvious heat-affected zone (HAZ) within one of the wires, like a gouge or slag ball (e.g., strands A34, A35, and B12). Despite the HAZ defects, these affected strands had residual capacities at least half the maximum load reported for the virgin strand. But the fracture was observed to occur on the elastic portion of the virgin strand reference curve. The residual capacities of remaining strands closest to the heat (A1, A30, A32, B6, B18, and B23) were between half and full capacity of the virgin strand. Similarly, the fracture was observed to occur on the elastic portion of the virgin reference curve. Of these six strands, the grease was completely burned away on four.
It is undesirable for the load–strain behavior of strands during the tension test to exhibit a fracture during the elastic response. However, defining an exact criterion to screen for this is difficult, as the design of stay cable bundles is based on ultimate tensile strength and does not necessarily rely on a certain level of ductility beyond the minimum elongation requirements in ASTM A416.(2) The Post-Tensioning Institute (PTI) does publish a specification covering the design, testing, and installation of bridge stay cables.(5) The fatigue strength of stay cables must be qualified by test according to this specification, and after the fatigue test is complete, the stay cable must be loaded and demonstrate a static strength of at least 92 percent AUTS. The static portion of this test ensures stay cables with fatigued wires have a minimum amount of residual strength in service. Understandably, the results reported herein were not performed in support of fatigue testing; however, the 92-percent criterion is an established bar for residual tensile strength of stay bundles. Table 4 reports the AUTS ratio for each thermal lance strand, and this could be compared to PTI’s 92 percent criterion. Using this criterion, strands A1, A30, A32, A34, A35, B6, B12, and B18 are considered to have failed. Therefore, based on the characteristics of these strands, it is conservatively recommended to visually inspect any strands for evidence of nicks, gouges, fused slag, or lacking any grease. If the visual inspection identifies any of these flaws, the strand is assumed to have no residual tensile strength.
Finally, in figure 30, it is seen that the load–strain response of strand B41 has higher offset response overall compared to the load–strain response of the virgin strands. This was seen with other thermal lance strand tests, though deleted from the plots due to shear failures. All test bundles were constructed from two different production lots of strand, and it is suspected that strands in the bundle used in the thermal lance cutting qualification test may have come from both production lots. This may explain the results from testing strand B41 (which may have come from the production lot with uncharacterized virgin strand tensile strength properties).
Strands selected from protected bundles subjected to specific blast events for residual capacity were chosen to represent three damage categories: across the spectrum of lateral deformation, maximum diameter, and intactness of the strand wires (i.e., intact, FBC, or IBC). Strands were first selected on the basis of the largest measured birdcage diameters and largest lateral measured deformations. Strands with this type of damage are thought to have the largest amount of cold working. Then, sampling selected strands representing a blend of all three damage categories, but selection focused primarily on identifying strands with the largest lateral deformation.
The strands recovered after the blast tests were obviously quite deformed, evident from the lateral deformation data presented in the Documentation chapter. The photo in figure 32 shows a view of the D38 strand before installation into the lower or upper grips of the tension test frame. This view shows the extreme bent shape of the strand. To grip the bottom portion of such a bent strand required a strong effort to bend it straight. This same strand is depicted in figure 20 once it was completely installed. The strong efforts included technicians bending the strand by hand and hitting the strand with a dead-blow hammer. Evidence that the installation stresses imposed were elastic was observed when the strand would spring back to its original bent shape after being removed from the grips. When installing birdcaged strands, the dead-blow hammer impacts tended to walk the birdcage up or down the strand or sometimes exacerbate its diameter slightly, but this was necessary to get the strand installed. Figure 33 shows strand G2 installed in the test machine. Strand G2 represented a test sample with one of the largest birdcage diameters.
The results from all the selected blast strands are presented in table 5 through table 7 for FBC, IBC, and intact strands, respectively. The load versus strain plots for all these strands are presented in figure 34 through figure 36, again, respectively for FBC, IBC, and intact strands. The trends in the data are easier to see in the three plots, and they will be discussed individually. Because of the curvature of the strands and presence of birdcages, some strands exhibited a softer response in the test compared to virgin strands, particularly at low loads. The soft displacement response was due to the force required to straighten the strand out or twist the strand back tight. To better compare the results, all data were shifted on the Strain axis such that the elastic portion of the curve would theoretically intersect zero strain. This was done by fitting a line through the data between a load of 10 and 40 kip and using the intercept with the Strain axis, as the offset shift applied to all the data.
—No data to report.
aCalculated by dividing AUTS by 64.14 kip, the average AUTS of virgin strand.
bShear failure in grip.
cImpact damage initiated the fracture.
dStatistical calculations ignore specimens with shear failures.
—No data to report.
aCalculated by dividing AUTS by 64.14 kip, the average AUTS of virgin strand.
bShear failure in grip.
cStatistical calculations ignore specimens with shear failures.
—No data to report.
aCalculated by dividing AUTS by 64.14 kip, the average AUTS of virgin strand.
bShear failure in grip.
cStatistical calculations ignore specimens with shear failures.
Figure 34 shows all the load–strain results from tension tests on FBC strands, and the soft loading response is pronounced. Generally, the load–strain behavior of these strands does not follow the reference curve of the virgin strand. The values of elastic moduli vary and show a much more gradual transition from elastic to strain hardening behavior when compared to the virgin strand curve. From the data listed in table 5 for FBC strands, all those without shear failures had AUTS ratios in excess of 92 percent; the average AUTS ratio was 98 percent. This implies, on average, the residual strength decreases about 2 percent for FBC strands. What also stands out from this batch of specimens is 8 of the 15 tested strands fractured within the gauge length of the specimen, and this did not happen in any virgin strand tests. The table footnotes indicate that for these eight strands, five of them had fractures initiated from impact damage to the strand. Impact damage is demonstrated in figure 37 from the fractured D41 strand. The arrows in the figure point to four areas where wires have impact impressions from other wires. During the blast event, strands are propelled into adjacent strands leading to these localized areas of cold work from impact. Since fractures did initiate out of these areas of impact damage, they obviously have an effect, but, on average, it is a small decrease in strength. As for the other three strands that fractured in the gauge without visual impact damage, it is possible there may have been impact damage present, but it was masked by necking of the wires near the fracture location.
The plots of load–strain data from tests of IBC strands are shown in figure 35. The average AUTS ratio was 99 percent, and these strands on average only show a 1-percent decrease in strength. The load–strain plots of strands that were categorized as intact are shown in figure 36; the average AUTS ratio was 1.00, indicating no loss in strength. The residual tensile capacity results between IBC and intact strand tests do not differ much, and the load–strain curves follow the virgin strand reference curve closely, with little initial soft behavior or deviation from the elastic slope. The notable exceptions in these two plots were the load–strain curves of tests on strand D38 (in figure 36) and D42 (in figure 35). Strand D42 had the largest lateral deformations of any strand tested. The soft behavior observed during the test of stand D42 corresponds to the straightening of the strand as observed in the majority of FBC strand tests. Strand D38 had one of the smallest lateral deformations but displayed soft behavior similar to strand D42. However, after reviewing the documentation photos, it was determined that strand D38 was fairly straight over the measured 24-inch-chord length. But, just beyond the chord measurement jig strand, D38 was very bent (see figure 38). Therefore, installing strand D38 in the testing machine would have caused another kink, which accounts for its soft behavior.
Figure 39 shows the influence of lateral deformation, vertical deformation, or birdcage diameter on the maximum load. The plot shows the average AUTS of virgin strands as a vertical dashed line to serve as the reference plane for ideal behavior. The three deformation variables are plotted relative to the virgin strength average. Looking at this plot, no discernible trend exists, as the maximum loads only vary from 60 to 66 kip over the entire range of deformations tested. Table 8 lists correlation coefficients calculated between the maximum load relative to one of the deformation variables (i.e., lateral, vertical, and diameter) and further segregated by damage type (i.e., FBC, IBC, and intact). Considering the smaller subsets of damage types, the correlation coefficients are small, indicating weak linear relationships—sometime positive and sometimes negative. Considering all the data together, there is a weak negative correlation between all the deformation variables, indicating strand strength decreases with an increase in vertical deformation, lateral deformation, or maximum diameter. Albeit, the values are nowhere near –1, indicating the poor linear fit.
—No data to report as all the diameters were the same.
Blasted strand testing focused exclusively on strands with all wires intact, and as discussed in the prior section, the strength of the strand was reduced only a couple percent. However, there was a small population of strands that had some wires fracture during the blast event. Hypothetically, strands with broken wires likely saw the greatest level of distress during the blast event, and it was prudent to investigate the residual strength of strands with some wires fractured. To explore this realm, strands in which six wires were fractured during the blast event were focused on with the reasoning that these particular wires would have been subjected to the most extreme loading if all the neighboring wires had fractured. Based on the histograms of damage presented in the Documentation chapter, there were only 12 blast-tested strands where 1 wire was intact. These wires were cut from their parent strand and tested in the same machine and same procedure as described in the “Virgin Wire” section.
The results of these 12 wire tests are summarized in table 9 and table 10 for outer and king wires, respectively. Load versus strain plots of the individual wires are shown in figure 40 and figure 41, for the outer and king wires, respectively. Only two blasted outer wires existed, and statistical evaluations cannot be performed on this small sample. However, from visual inspection of the load versus strain plots in figure 40, these wires could not achieve much ductility fracturing around 1.4 percent elongation. As for the king wires, eight of them were considered valid because they broke in the gauge length over a wide variety of elongations.
Each of the tables reports the AUTS ratio for each wire tested. Only 10 wires had valid results breaking in the gauge, and of those, 4 failed to meet the PTI 92 percent residual strength criterion and would be considered totally failed. However, not all the wires failed the PTI criterion, and it would be punitive to neglect the contribution of strength from strands with 6 wires cut; therefore, it was considered prudent to average the results together for the 10 valid tests. The average AUTS ratio was 0.93, indicating that strands with six wires broken have only about 7 percent reduction in strength.
| Strand | AUTS (kips) |
AUTS Ratioa |
Strain at AUTS |
Elongation (percent) |
Notes |
|---|---|---|---|---|---|
| E2 | 7.80 | 0.83 | 0.0139 | 1.41 | Broke in gauge |
| G84 | 8.70 | 0.93 | 0.0144 | 1.45 | Broke in gauge |
aCalculated by dividing AUTS by 9.37 kip, the average AUTS of virgin outer wire.
—No data to report.
aCalculated by dividing AUTS by 10.15 kip, the average AUTS of virgin king wire.
bResults neglected from statistical calculations, since fracture occurred at grip.
cThis wire had an initially necked region within the gauge length and failed at this location. The result was considered a premature failure and censored from statistical calculations.
Going back to table 5 through table 7, FBC strands exhibited a 2-percent reduction in strength, and IBC strands exhibited a 1-percent reduction in residual maximum load. Intact strands had no reduction in residual maximum load. Null hypothesis tests were performed using a Wilcoxon rank-sum test hypothesizing there was no difference between the mean of the virgin strand and the means of FBC, IBC, or intact strands. The hypothesis was rejectable for FBC- and IBC-damaged strands even down to the two-tailed 0.01 significance level, indicating there was a statistical difference between these two damage types. The hypothesis was confirmed for the intact strands, indicating their mean strength was statistically identical to the virgin strand. Considering only FBC and IBC damage are statistically significant, it is recommended that an overall reduction factor be applied to the entire bundle to account for the reduction in strength from a blast event. Applying such a factor would alleviate the need to carefully inspect for birdcages or deformation as part of qualification.
Defining an overall blast reduction factor must also consider the notion that single wires were tested from strands with six fractured wires in this project. In this extreme example, there was only a 7-percent reduction in average strength in lieu of 2 percent for FBC strands. Considering the population of strands with zero to seven wires broken, and proportioning out a reduction in capacity between 7 and 2 percent to those populations, the overall mean blast reduction factor is 0.97. Statistics are provided in the report to account for uncertainty, but taking a more simplistic approach, a mean bundle blast reduction factor of 0.95 is recommended. This would inherently account for some uncertainty, but it is considered conservative because intact strands had no reduced capacity. The blast reduction factor should be applied to all intact wires in a qualification test. As an example, referring back to the histogram of damage for bundle G in figure 14, that bundle had 697 wires survive, though considering a blast reduction factor of 0.95, only 662 wires (i.e., 697 times 0.95) survived when comparing to the acceptance criteria, and no further work must be done to evaluate deformation or birdcaging or to account for impact damage to wires.