U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-13-060 Date: June 2013 |
Publication Number: FHWA-HRT-13-060 Date: June 2013 |
This chapter summarizes information about the various mechanical properties that are relevant to the structural design of UHPC components.
It is important to note that the dispersion and orientation of the fiber reinforcement are critical parameters that influence the mechanical behavior of UHPC. The fiber reinforcement serves to resist tensile stresses in the UHPC component both before and after tensile cracking of the UHPC matrix. Post-cracking mechanical response of UHPC is particularly susceptible to degradation from disadvantageous fiber dispersion and/or orientation. Mixing and placing methods can affect the hardened UHPC mechanical response and thus must be appropriately coordinated to ensure acceptable mechanical performance.(4)
Compressive strength is an important property in the design of any concrete structure. It is also the property that is most frequently measured. As discussed in the previous chapter, cylinder and cube compression test methods used for conventional concrete are appropriate for the determination of UHPC compressive strength. Minor modifications to the test and analysis methods may be required.
Graybeal reported the compressive strengths of nearly 1,000 specimens subjected to the following four different curing conditions:(22)
Most tests were conducted on 3- by 6-inch (76- by 152-mm) cylinders with the ends ground so that they were parallel within 1 degree. Tests generally used the procedures of ASTM C39, except the loading rate was increased to 150 psi/second (1 MPa/s), and a 6.5-inch (165-mm)-diameter spherical bearing plate was used.(67)
The average measured compressive strengths at 28 days for six cylinders cured using methods a, b, c, and d were 28.0, 24.8, 24.8, and 18.3 ksi (193, 171, 171, and 126 MPa), respectively. Density of the UHPC ranged from 150 to 156 lb/ft3 (2,400 to 2,500 kg/m3). Within each curing regime, there was a slight increase in compressive strength as the density increased.
Graybeal also investigated the effect of cylinder and cube size on the measured compressive strength using 2- by 4-inch, 3- by 6-inch, 4- by 8-inch, and 3- by 6.5-inch (51- by 102-mm, 76- by 152-mm, 103- by 203-mm, and 76- by 165-mm) cylinders and 2- and 3.94-inch (51- and 100-mm) cubes.(22,60)
The measured strengths were all within 8 percent of the control 3- by 6-inch (76- by 152-mm) cylinder strength. The cubes had compressive strengths about 5 percent higher than the cylinders. Similar results were also observed by Orgass and Klug.(68) The smaller cylinders and cubes had a larger standard deviation.(22) Magureanu et al. reported that 3.9-inch (100-mm) cubes had a 20-percent lower measured compressive strength than 2.0-inch (50-mm) cubes.(69)
Graybeal also indicated that loading rates between 35 and 245 psi/seconds (0.24 and 1.7 MPa/seconds) had no noticeable effect on the measured compressive strength, modulus of elasticity, and Poisson's ratio.(22)
Skazlic et al. investigated the effect of cylinder size on the compressive strength of 10 different UHPC mixtures.(70) Cylinder diameters were 2.75, 4, and 6 inches (70, 100, and 150 mm) with a length-to-diameter ratio of 2:1. Assuming a 4- by 8-inch (100- by 200-mm) cylinder as a standard, the authors proposed conversion factors of 1.05 to 1.15 for strengths measured on 2.75- by 5.5-inch (70- by 140-mm) cylinders and 0.85 to 0.95 for strengths measured on 6- by 12-inch (150- by 300-mm) cylinders.
Based on a regression analysis of the data for the particular mix tested, Graybeal determined that the compressive strength gain of UHPC cured under standard laboratory conditions can be represented by the equation in figure 1 for any time after 0.9 days.(22)
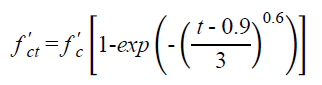
Figure 1. Equation. Compressive strength gain at any age after casting from Graybeal(22)
where:
f'c t = UHPC compressive strength at age tdays
f'c = UHPC compressive strength at 28 days
t = time after casting in days
Graybeal recently completed a follow-on study focused on a readily available UHPC that is formulated for use in field-cast connection applications. (47) A single mix design was cured at 105 °F (41 °C), 73°F (23 °C), and 50 °F (10 °C) to assess the rate of compressive mechanical property development. The time to initiation of compressive mechanical strength gain is provided in figure 2. The relationship between curing temperature and compressive strength is provided in figure 3. The fitting parameters relevant to figure 3 are in table 6.
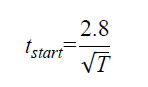
Figure 2. Equation. Relationship between curing temperature and initiation of rapid compressive strength gain from Graybeal(47)
where:
tstart= time of initiation of strength gain in days
T = curing temperature in degrees Celsius
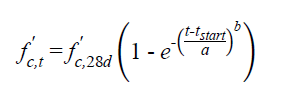
Figure 3. Equation. Relationship between time after mix initiation and compressive strength as a function of curing temperature from Graybeal(47)
where:
f'c 28 d = compressive strength at 28 days
f'c, t = compressive strength at time t in days after mix initiation
tstart = time of initiation of strength gain in days
a = fitting parameter in days
b = dimensionless fitting parameter
| Curing Regime | T(°C) | f'c,28d (ksi) | a (days) | b |
|---|---|---|---|---|
| 105°F (41 °C) | 41 | 24.5 | 0.25 | 0.25 |
| 73° F (23 °C) | 23 | 24 | 1.0 | 0.30 |
| 50° F (10 °C) | 10 | 22.5 | 4.0 | 0.50 |
Note: 1 ksi = 6.89MPa and °F = 1.8 X °C + 32 |
||||
Kazemi and Lubell also investigated compressive strength as a function of time after casting.(27) The response of a locally sourced UHPC from central Canada was found to correspond to the relationship in figure 3, with a equal to 4 and b equal to 0.5 or 0.6 depending on the fiber content.
Schmidt and Fröhlich reported that irregularities in the loaded surface of specimens tested in compression caused a more pronounced decrease in the measured compressive strength in UHPC than was evident with conventional concrete.(71)
Tests of UHPC in axial compression at elevated temperatures showed that the measured compressive strength decreases as the concrete temperature at testing increases.(72,73) However, some or all of the strength is recovered after the specimens cool down.
Richard reported that compressive strengths as high as 80 ksi (550 MPa) can be achieved at atmospheric pressure and heat treating at 480 °F (250 °C). (12) With pressure, compressive strengths as high as 117 ksi (810 MPa) are possible. With conventional production capabilities and curing at 194 °F (90 °C), strengths of 40 ksi (280 MPa) can be achieved.
Tests of UHPC under biaxial compression have been reported by Curbach and Speck and Leutbecher and Fehling.( 74,75)
Additional compressive strength data are available in many of the publications about research and applications of UHPC. These data indicate that the initiation of strength gain and subsequent rate of strength gain depend on the particular UHPC constituent materials, mix proportions, and the curing conditions.
In conventional structural design for concrete bridges, the tensile strength of concrete is assumed to be zero in reinforced concrete design and often taken as 6√fc ` in prestressed concrete girder design.(76)
The tensile strength of UHPC is higher than that of conventional concrete, and UHPC can exhibit sustained tensile strength after first cracking. The results of tests for tensile strength of UHPC, therefore, often report a value of first cracking strength as well as a peak post-cracking strength. Consequently, tensile strength takes on increasing importance as a property to consider in design.
An example tensile stress-strain response obtained from a readily available UHPC containing 2 percent by volume steel fiber reinforcement was captured by Graybeal and is shown in figure 4.(77) The results shown were developed as part of a study.(78,79)
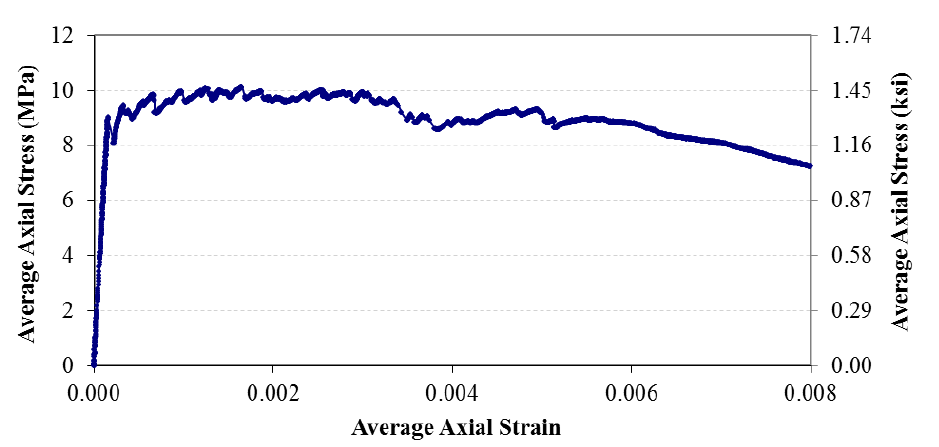
Figure 4. Graph. Tensile stress-strain response of UHPC(77)
Graybeal has proposed the idealized tensile stress-strain response shown in figure 5.(79) This response is based on direct tension tests of two UHPCs with multiple fiber contents. It is proposed as a conceptual illustration of the precracking and postcracking tensile stress-strain response of strain-hardening fiber reinforced concretes, such as UHPC. The behavior is divided into four phases. Phase I is elastic behavior. Phase II is the phase wherein multiple tightly spaced cracks form in the UHPC matrix. The cracks occur individually as the stress in the matrix exceeds the matrix cracking strength. Phase III begins at the strain level where additional cracking between existing cracks is unlikely. Individual cracks widen in this phase. Lastly, Phase IV begins when an individual crack has reached its strain limit and the fibers bridging that crack begin to pull out of the matrix. In a strain-hardening fiber-reinforced concrete, the fiber bridging strength where localization occurs is greater than the cracking strength where multicracking occurs.

Figure 5. Graph. Idealized uniaxial tensile mechanical response of a UHPC(79)
Standard tensile test methods designed to assess the cracking strength of conventional concrete may be appropriate for assessing the first crackingstrength of UHPC, but are unlikely to be appropriate for quantitatively assessing the post-cracking tensile response of UHPC.(22) The ASTM C78—Standard Test Method for Flexural Strength of Concrete (Using Simple Beam with Third-Point Loading) and ASTM C496—Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens fall into this category.(80,81) Both test methods include assumptions of mechanical behaviors that are not consistent with strain-hardening fiber-reinforced concretes and thus are likely to overestimate the tensile strength of the UHPC.
Graybeal has proposed a modified version of ASTM C496.(82) The modified test method includes a requirement to monitor the first cracking of the UHPC during the test and calculate the splitting tensile strength based on the observed first cracking load.
Flexure-based test methods have been proposed, and in some cases, standardized. ASTM C1018 (withdrawn), ASTM C1609, and RILEM TC 162-TDF all presenttest methods for use in determining the tensile response of fiber-reinforced concretes.(83,84,85) Methods have been proposed for analyzing the test results so as to develop uniaxial tensile response curves. (See references 4, 85, 86, and 87.) However, these types of flexure tests have been demonstrated to be susceptible to overindications of strength as a result of the use of inappropriate support conditions.(88)
A variety of direct tension test methods have been developed. In a direct tension test, the UHPC specimen is loaded in uniaxial tension and thus the tensile response can be directly captured by measuring the load on and the strain experienced by the specimen. Direct tension tests can be divided into two groups, namely, tests that allow rotation of the ends of the test specimen and tests that do not. The tests with rotation might provide an indication of first cracking strength, but are not appropriate for assessment of post-cracking behaviors. This is because local inconsistencies in stiffness at the plane of the first crack result in rotation and fiber pullout at this crack prior to the generation of a full set of additional cracks. Fixed-end tests that do not allow rotation at cracks are appropriate for capturing the full tensile stress-strain response. However, these tests are difficult to complete because of the bending stresses that can be imparted to the specimen during initial setup.
Graybeal reported measurements of tensile strength using flexural prisms, split cylinders, mortar briquettes, and direct tension tests of cylinders. (22) The combined results of these tests indicated a first tensile cracking strength of approximately 1.3 ksi (9.0 MPa) for steam-cured specimens and approximately 0.9 ksi (6.2 MPa) without any heat treatment.
The modulus of rupture values for first cracking determined by the ASTM C1018 prism flexure test varied from 1.3 to 1.5 ksi (9.0 to 10.3 MPa), depending on the method of steam curing, and had an average value of 1.3 ksi (9.0 MPa) for untreated specimens.(83) These specimens exhibited large deflections before the post-cracking peak load was reached.
In the split cylinder tests (ASTM C496), measured splitting tensile strengths at first cracking were 1.7 ksi (11.7 MPa) for steam-cured specimens and 1.3 ksi (9.0 MPa) for untreated specimens. (81) For the steam-cured specimens, the splitting tensile strengths at first cracking varied from 3 to 5 percent of the measured compressive strength. The post-cracking peak tensile splitting stresses ranged from 12 to 16 percent of the compressive strength.
First cracking tensile strengths using briquettes in accordance with AASHTO T 132 ranged from 1.0 to 1.4 ksi (6.9 to 9.7 MPa), depending on the method of steam curing. For untreated specimens, the average value was 0.9 ksi (6.2 MPa).(89)
In the direct tensile tests of 4- by 8-inch (102- by 203-mm) cylinders, first tensile cracking occurred between 1.1 and 1.6 ksi (7.6 and 11.0 MPa), depending on the method of steam curing, and between 0.8 and 1.0 ksi (5.5 and 6.9 MPa) for untreated specimens.
In this study, Graybeal concluded that the tensile strength (fct) of UHPC can be related to the measured compressive strength ( f'c) by the equation in figure 6.
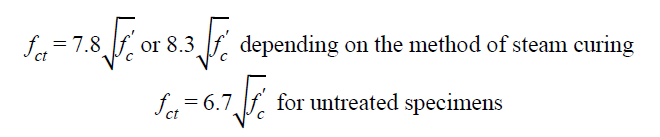
Figure 6. Equation. Concrete tensile strength approximations
Subsequent research by Graybeal and Baby on this topic has resulted in the development of a uniaxial direct tension test method applicable to UHPC. (79) This test method, whose concept is based on a standard tension test applied to metals, provides the uniaxial tensile mechanical response of UHPC and is applicable to both cast and extracted test specimens. Tests were completed on two UHPCs containing multiple steel fiber reinforcement percentages and cured through ambient laboratory and steam-treated conditions. The results demonstrated that these two UHPCs could sustain more than 1.3 ksi (9 MPa) of uniaxial tensile load through a strain of at least 4,000 millionths.
Baby, Graybeal, Marchand, and Toutlemonde investigated the use of flexural tensile test methods for UHPC and the associated analyses necessary for appropriate interpretation of the results.(86) These analyses, often referred to as inverse analyses, derive the uniaxial tensile response from the observed load, deflection, and possibly surface strains observed during a flexure prism test. This research demonstrated that flexure test methods can be applied, but that capture of specific response observations are necessary and appropriate interpretationof data is critical. This research was conducted alongside the research presented in Graybeal and Baby, allowing direct comparison of results. (79)
Reineck and Frettlöhr investigated the effect of specimen size on the flexural and axial tensile strengths.(90) The depth of the flexural specimens ranged from 1 to 6 inches (25 to 150 mm) with width-to-depth ratios ranging from 1 to 5. The same sizes and ratios were used for the axial tension tests. The authors reported a decrease in both strengths with increasing size of the test specimens.
Schmidt and Fröhlich observed that specimens heat cured at 194°F (90 °C) for 48 hours and tested in flexure had a 15-percent higher flexural strength than specimens stored continuously at 60 °F (20 °C).(71)
A study by Wille and Parra-Montesinos investigated the effects of beam size, casting method, and support conditions on UHPC flexure test results. Thestudy reported that large discrepancies in results were possible for an individual UHPC, depending on the test setup and specimen characteristics. (88)
Flexural strengths have also been reported by others. (See references 39, 69, 91, 92, 93, and 94.)
Axial tension tests have also been reported by others. (See for example references 75, 95, 96, 97, 98, 99, 100, and 101.)
Biaxial compression-tension tests have been reported by Leutbecher and Fehling and by D'Alessandro et al.(75,102)
Graybeal measured the modulus of elasticity in compression in accordance with ASTM C469 at ages from 1 to 56 days for cylinders cured according to the four regimes described under Compressive Strength.(22,103) Reported values were mostly the average value of six cylinders. After steam curing, the measured values were about 7,250 ksi (50 GPa). Cylinders cured under standard laboratory conditions had modulus of elasticity values of about 6,200 ksi (42.7 GPa) at 28 days. In terms of strength, modulus of elasticity, and strain at peak load, the UHPC showed very little change after completion of steam curing. The specimens cured under laboratory conditions continued to gain strength for at least 8 weeks after casting but the increase in modulus of elasticity and the decrease in strain at peak load seemed to stop at about 1 month.
The modulus of elasticity was also measured in direct tension tests. The average measured values were 7,500 ksi (51.9 GPa) for steam-treated specimens and 6,900 ksi (47.6 GPa) for untreated specimens. These values were slightly higher than measured in compression.
The equation in figure 7 or modulus of elasticity was proposed by Graybeal based on the general form of the AASHTO equation and values of f'c between 4.0 and 28.0 ksi (28 to 193 GPa).(22)
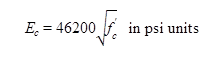
Figure 7. Equation. Graybeal equation for UHPC modulus of elasticity(22,103)
where:
Ec = modulus of elasticity
f'c = UHPC compressive strength
Subsequent research by Graybeal has developed additional results related to the modulus of elasticity of UHPC.(47) These tests, completed on a UHPC specifically formulated for use as a field-cast material in connections between structural components, found that the equation in figure 8 is inappropriate for strengths between 14 and 26 ksi (97 and 179 MPa). This research also investigated the impact of curing temperature on compressive mechanical response development and found that the modulus of elasticity is related to the compressive strength and is largely independent of curing temperature.
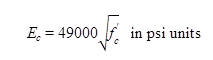
Figure 8. Equation. Graybeal equation for UHPC modulus of elasticity(47)
Ma et al. developed the equation in figure 9 for UHPC containing no coarse aggregates:(104)
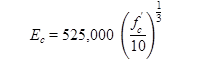
Figure 9. Equation. Ma et al. equation for UHPC modulus of elasticity(104)
Modulus of elasticity values have also been reported by others. (See references 91, 92, 94, and 105.)
Diederichs and Mertzsch measured the stress-strain relationships at concrete temperatures ranging from 68 to 1,560 °F (20 to 850 °C).(73) They observed a large reduction in both strength and modulus of elasticity at the higher testing temperatures. At the same time, the strain at peak stress increased at the higher temperatures. The same observations were made by Pimienta et al. for temperatures ranging from 68 to 1,110 °F (20 to 600 °C).(72) However, some or all of the loss was recovered after the specimens cooled down.
Table 7 lists values of Poisson's ratio determined by various researchers.
| Poisson's Ratio | Reference (First Author) |
|---|---|
| 0.2 | Simon(106) |
| 0.16 | Joh(107) |
| 0.21 | Ahlborn(108) |
| 0.19 | Bonneau(105) |
| 0.18 | Graybeal(109) |
| 0.18 | Ozyildirim(45) |
Ocel and Graybeal reported a fatigue test of an AASHTO Type II girder.(110) The upper limit of the fatigue load was just below the static load levels that would cause flexural and shear cracking of the girder. The first cracks were observed after 0.64 million cycles at the intersection of the web and bottom flange in one shear span. After 1.405 million cycles, the same cracks were observed in the other shear span. Flexural cracks were noticed in the constant moment region after 1.888 million cycles. These were accompanied by a longitudinal crack in the bottom flange. Testing continued to 12 million cycles, during which the existing cracks continued to lengthen and additional cracks occurred, but there was no indication of fatigue degradation or change in the global behavior of the girder.
Prior to construction of a UHPC bridge in the city of Calgary, a 39-inch (1-m)-long transverse section was tested in flexural fatigue.(111) The section was subjected to 1 million cycles between 20 and 80 percent of the design service load, 1 million cycles between the 20 and 80 percent of the observed first cracking load, and 1 million cycles between 20 and 80 percent of the failure load for companion sections that contained fiber-reinforced plastic reinforcing bars. Following the fatigue testing, the specimen was loaded to failure with the maximum load being greater than expected.
Prior to construction of a UHPC waffle-slab bridge deck in Wapello County, IA, tests were conducted on specimens representing a full-scale portion of the bridge.(112,113) A single point load representing a wheel load was placed at two critical locations. No fatigue damage was noted after 1 million cycles of loading at each location.
Graybeal and Hartmann conducted flexural fatigue tests on 2-inch (51-mm)-square beams.(114) In one set of tests, uncracked specimens were loaded to produce different stress ranges. Most specimens survived more than 6 million cycles of loading. In a second series of tests, the specimens were precracked and then tested in fatigue with loads cycling from 10 to 60 percent of the cracking load. One specimen failed after 9,950 cycles, while the other failed after 129,700 cycles. In these tests, some of the steel fiber reinforcement was observed to have fractured rather than pulling out of the UHPC matrix.
Schmidt et al. investigated the fatigue behavior of UHPC cylinders loaded in axial compression at various stress range levels.(115) They observed that specimens with a ratio of stress range to compressive strength of 0.45 survived 2 million load cycles without failure. The test specimens that survived the 2 million cycles of loading had only a slight decrease in compressive strength compared with specimens without any preceding load cycles.
Fatigue tests of UHPC specimens under various combinations of stress level and stress range by Fitik et al. showed a range of cycles to failure from 2.5 to more than 7.0 million cycles.(116) They attributed the wide range to local faults, which initiated the failure process.
Uniaxial compression tests reported by Grünberg et al. and Lohaus and Elsmeier with a minimum stress limit of 5 percent of the static strength andvarying upper stress level resulted in the number of cycles to failure ranging from about 2.5 to 7.1 million.(117,118)
Behloul et al. conducted flexural fatigue tests on 4- by 4- by 16-inch (100- by 100- by 400-mm) prisms made of two different UHPC formulations. (119) Prior to fatigue loading, the specimens were loaded to produce a crack opening of 0.012 inches (0.3 mm). The specimens were then cycled at 5 Hz between 10 and 90 percent of the first cracking strength. After 1 million cycles, the specimens were loaded statically, and the results were compared with specimens not subjected to fatigue loading. The fatigue loading appeared to have no effect on the overall mechanical behavior.
Lappa et al. reported flexural fatigue tests of 5- by 5- by 40-inch (125- by 125- by 1,000-mm) beams with a maximum load equal to about 75 percent of the static strength.(120) The number of cycles to achieve fatigue fracture ranged from 29,295 to 170,771.
Coefficients of thermal expansion (COTE) measured by various researchers are shown in table 8.
| COTE | Reference First Author |
|
|---|---|---|
| Millionths/°F | Millionths/°C | |
| 8.2 to 8.7 | 14.7 to 15.6 | Graybeal(22) |
| 6.7 | 12 | Fehling(121) |
| 5.6 to 6.7 | 10 to 12 | Simon(106) |
| 7.6 to 8.2 | 13.6 to 14.8 | Ahlborn(108) |
| 6.7 | 12 | Behloul(122) |
The French Interim Recommendations state a value of 6.1 x 10-6/°F (11 x 10-6/°C) if no other value can be determined.(4)
Graybeal measured heat of hydration in a well-insulated calorimeter and reported a temperature rise of about 65 °F (36 °C).(22)
Carbonell et al. investigated the bond strength between conventional concrete substrates and UHPC toppings.(123) Primary variables were surface temperature and moisture condition of the substrate. Half the specimens were subjected to 300 freeze-thaw cycles in accordance with ASTM C666 Method B. (124) The authors evaluated bond strength using an indirect splitting tensile test along the interface. Samples subjected to the freeze-thaw tests had greater bond strength than samples of the same age without freeze-thaw cycles. Samples in which the substrate was saturated before placing the UHPC achieved higher bond strengths than samples with a dry substrate.
Bindiganvile et al. compared the impact resistance of UHPC with that of conventional fiber reinforced concrete (FRC).(125) Under quasistatic loading, UHPC was two to three times stronger in flexure and absorbed three times greater energy than conventional steel FRC or polypropylene FRC. Under impact loading, the UHPC was approximately twice as strong as conventional FRC and dissipated three to four times as much energy.
Cadoni et al. observed that the first cracking stress under dynamic loading was two to three times greater than under static load.(126) The impact resistance of UHPC for use in piles was investigated by Leonhardt et al.(127)
Further discussion of impact resistance can be found in chapter 6 under the discussion of security applications.
The standard test method for creep in North America is ASTM C512.(128) In this test, specimens are subjected to a constant axial stress, and the change in length over time is measured. Results may be expressed as a creep coefficient = creep strain/initial strain or specific creep = creep strain/applied stress.
Graybeal conducted creep tests on 4-inch (102-mm)-diameter cylinders loaded at ages of 4, 21, and 28 days depending on the method of curing. (22) Creep coefficients after 1 year ranged from 0.29 to 0.78, and specific creep ranged from 0.04 to 0.15 millionth/psi (5.7 to 21.2 millionths/ MPa), depending on the method of curing and loading age. For reference, the specific creep of conventional concrete is in the range of 0.25 to 1.0 millionths/psi.
Graybeal also conducted creep tests on 4-inch (102-mm) diameter cylinders with compressive strengths between 8.0 and 13.0 ksi (55 and 90 MPa) at stress-to-strength ratios ranging from 0.60 to 0.85 to represent the application of prestressing forces prior to steam curing. Measured creep coefficients after 30 min under sustained load ranged from 0.32 to 0.85. These values would be considered high for the short duration of loading.
Burkhart and Müller measured the effect of age of loading, specimen size, stress level, and curing conditions (sealed and unsealed) on the creep of UHPC.(129) Reported specific creep values after about 100 days under load ranged from 0.11 to 025 millionths/psi (16 to 35 millionths/MPa). Measured creep coefficients after 100 days under load were between about 0.9 and 1.3. The measured creep was observed to decrease with age at loading and increased specimen size. This behavior is similar to that of conventional concrete.
Ichinomiya et al. reported specific creep values ranging from 0.19 to 0.28 millionths/psi (28 to 40 millionths/MPa) after 150 days under load for specimens loaded at 2 and 4 days.(92) For specimens loaded at 28 days, the specific creep was about 0.08 millionths/psi (11 millionths/MPa) after about 120 days.
Acker and Behloul reported specific creep values between 0.30 and 0.22 millionths/psi (43 and 32 millionths/MPa) for ages of loading between 4 and 28 days.(130) Fehling et al. reported specific creep values between 0.32 and 0.15 millionths/psi (47 and 22 millionths/MPa) and creep coefficients between 2.27 and 1.08 for ages of loading between 1 and 28 days.(121)
Francisco et al. reported creep strains of about 1,000 millionths after 30 days under load at a stress of about 8.7 ksi (60 MPa), corresponding to a specific creep of about 0.12 millionths/psi (17 millionths/MPa).(131) The 2.75-inch (70-mm)-diameter cylinders were cured at 122 °F (50 °C) prior to loading at an age of 2 days. Drying creep was negligible.
Francisco et al. showed that the specific creep was about the same for heat-treated UHPC specimens loaded at an age of 2 days to 25 and 40 percent of the compressive strength.(132) Flietstra et al. investigated the creep caused by applying a compressive stress and then subjecting the loaded specimens to different curing regimes.(133)This test simulated transfer of the prestressing force prior to heat treatment.
Two types of shrinkage may be present in UHPC. Drying shrinkage is that caused by loss of moisture from the UHPC. Autogenous shrinkage is that caused by a decrease in volume as the cementitious materials hydrate. The standard test in the United States for measuring shrinkage is ASTM C157, which is designed to measure drying shrinkage beginning after the concrete has hardened.(134) Other methods are used to measure autogenous shrinkage because these measurements must begin immediately after the UHPC is placed.
Shrinkage of UHPC measured in accordance with ASTM C157 using 3- by 3-inch (76- by 76-mm) prisms provided an ultimate shrinkage range of 620 to 766 millionths, depending on the method of steam curing, and 555 millionths for untreated specimens.(22) The initial shrinkage rate of UHPC was also measured in separate tests. During the initial hydration period, peak shrinkage of 64 millionths/hour was measured. As much as 400 millionths of shrinkage occurred in the first 24 hours for untreated specimens. Following steam curing, further shrinkage was almost eliminated.(22,130)
Measurements of shrinkage by Burkhart and Müller starting 1 or 2 days after casting showed no difference between sealed and unsealed cylinders and among specimens with diameters of 3, 4, and 6 inches (75, 100, and 150 mm).(129) They attributed most of the shortening to that caused by autogenous shrinkage, with very little caused by drying shrinkage. All values were about 300 millionths after 200 days of measurements. Autogenous shrinkage values of 600 to 900 millionths at 28 days were reported by Eppers and Müller, 200 to 550 millionths at 150 days byIchinomiya et al., and about 640 millionths at 365 days by Lallemant-Gamboa et al.(135,92,93)
Fehling et al. reported total shrinkage of 700 and 900 millionths at 7 and 28 days, respectively, for sealed specimens. For specimens subjected to heat treatment, the subsequent shrinkage was negligible.(121)
Francisco et al. reported autogenous shrinkage of about 270 millionths and drying shrinkage of about 100 millionths at 350 days on 2.75-inch (70-mm)-diameter cylinders cured at 122 °F (50 °C).(131)
Ma et al. showed that the autogenous shrinkage could be reduced considerably by including a basalt coarse aggregate with an aggregate size ranging from 0.08 to 0.40 inches (2 to 5 mm).(104) The coarse aggregate had a relatively small effect on the fresh concrete properties, compressive strength, and modulus of elasticity. Significant reduction of early age autogenous shrinkage was obtained by replacing silica fume with metakaolin in specimens cured at 68 °F (20 °C).(136) For UHPC cured at 108 °F (42 °C), the total shrinkage measured for a mix containing metakaolin was negligible compared with mixes with silica fume or fly ash.(110)
To offset the magnitude of autogenous shrinkage, Suzuki et al. and Kim et al. investigated the use of an expansive additive and a shrinkage reducing additive.(137,138) Suzuki et al. reported that an autogenous shrinkage of more than 700 millionths would be reduced to zero with the use of these materials. Kim et al. reported that total shrinkage at 90 days was reduced from 800 to 400 millionths.
The application of heat curing has a significant and immediate impact on the mechanical properties of UHPC. It increases the compressive strength, tensile cracking strength, and modulus of elasticity. It decreases creep and virtually eliminates subsequent shrinkage. These beneficial properties can also be achieved without heat curing. However, the effect is reduced, and it takes a longer time to achieve the beneficial properties.
Sufficient information has been published about the mechanical properties of UHPC to establish a range of properties to consider in structural design. These are listed in table 9.
| Property | Range | |
|---|---|---|
| Compressive strength | 20 to 30 ksi | 140 to 200 MPa |
| Tensile cracking strength | 0.9 to 1.5 ksi | 6 to 10 MPa |
| Modulus of elasticity | 6,000 to 10,000 ksi | 40 to 70 GPa |
| Poisson's ratio | 0.2 | 0.2 |
| Coefficient of thermal expansion | 5.5 to 8.5 millionths/°F | 10 to 15 millionths/°C |
| Creep coefficient1 | 0.2 to 0.8 | 0.2 to 0.8 |
| Specific creep1 | 0.04 to 0.30 millionths/psi | 6 to 45 millionths/MPa |
| Total shrinkage2 | Up to 900 millionths | Up to 900 millionths |
1 Depends on curing method and age of loading. 2 Combination of drying shrinkage and autogenous shrinkage and depends on curing method. |
||
Creep of UHPC is much less than conventional concrete. This results in reduced prestress losses but can be detrimental if relied on to reduce stresses in restrained members.
The total shrinkage reported in table 9 includes both drying and autogenous shrinkage. From the reported data, most of the shrinkage is autogenous shrinkage.
UHPC has sufficient fatigue resistance in both tension and compression to resist several million cycles of loading. Its impact strength is two to three times higher than its static strength.