U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-13-060 Date: June 2013 |
Publication Number: FHWA-HRT-13-060 Date: June 2013 |
This chapter summarizes available information about the structural design of UHPC members and the testing that has been performed on structuralmembers. The different sections in this chapter correspond to articles in the AASHTO Load & Resistance Factor (LRFD) Bridge Design Specifications. (76)
As noted in chapter 3, it is important to recognize that the dispersion and orientation of the fiber reinforcement are critical parameters that influence the structural behavior of UHPC. The fiber reinforcement serves to resist tensile stresses in the UHPC component both before and after tensile cracking of the UHPC matrix. Post-cracking structural response of UHPC is particularly susceptible to degradation from disadvantageous fiber dispersion and/or orientation. Mixing and placing methods can affect the hardened UHPC mechanical response and thus must be appropriately coordinated to ensure acceptable structural performance. A framework for addressing the reliance on fiber reinforcement in the tensile mechanical resistance of UHPC structural components has been presented in the Service d'étude des transports, des routes et de leurs aménagement-Association Francaise de Genie Civil (SETRA-AFGC) design recommendations.(4)
The calculated flexural resistance of concrete components is generally based on the conditions of equilibrium of forces and strain compatibility. The usable compressive strain in unconfined concrete is limited to a maximum value of 0.003. The shape of the stress-strain curve may be any shape that results in a prediction of strength in substantial agreement with test results. For simplification, a rectangular stress block for the compression zone is usually assumed. The tensile strength of the concrete is neglected. The applicability of this approach for use with UHPC has been addressed in several articles.
Graybeal tested a 36-inch (0.91-m)-deep AASHTO Type II girder made of UHPC in flexure using four-point bending on a span length of 78.5 ft (23.9 m). (109) (See figure 10.) The girder contained twenty-four 0.5-inch (12.7-mm)-diameter strands. Prior to reaching peak load, the girder achieved a deflection of almost 19 inches (480 mm) and failed by a combination of tensile fracture of the strands and pullout of the fibers.

Figure 10. Photo. Flexural test of an AASHTO Type II girder made of UHPC
The peak applied load on the girder produced a bending moment of 38,700 kip-inches (4,370 kN-m). A flexural analysis, assuming a rectangular stress block and that the UHPC carried no tensile forces after cracking, produced a calculated moment capacity of 27,840 kip-inches (3,150 kN-m)—considerably less than the measured strength. Based on analysis of the measured data, Graybeal proposed that flexural capacity could be calculated more accurately assuming the following UHPC stress-strain curve:
For his test data, stress-strain relationships would be as follows:
The flexural strength of the section can then be calculated using a traditional mechanics of materials approach.
Graybeal also tested two pi-girders made of UHPC in flexure using four-point bending.(139) The span lengths of the girders were 69 and 45 ft (21 and 13.72 m). The girders achieved deflections of about 10 and 5 inches (250 and 125 mm) before reaching a peak load. The failure mechanisms of the two girders were similar. The fibers began to pull out from the matrix at a crack near midspan. This shed the tensile force from the fibers to the prestressing strands, which then fractured. The moments at first flexural cracking of the girders were 20,600 and 19,500 kip-inches (2,330 and 2,200 kN-m). The ultimate flexural capacities of the girders were 37,600 and 38,190 kip-inches (4,250 and 4,310 kN-m). A third girder that was intended to fail in shear failed in flexure at a moment of 36,720 kip-inches (4,150 kN-m). Based on an analysis in accordance with the AASHTO LRFD Bridge Design Specifications, a 70-ft (21.3-m) girder has a Service III moment demand of 19,940 kip-inches (2,250 kN-m) and Strength I moment demand of 39,600 kip-inches (4,470 kN-m). The cracking moments observed in the experiment were approximately equal to the Service III moment. The measured flexural capacities were, on average, about 5 percent less than the required values, indicating the need for additional flexural reinforcement.
Meade and Graybeal reported the results of sixteen 6-inch (152-mm)-wide, 15-inch (381-mm)-deep rectangular UHPC beams tested in four-point bending over a span length of 16 ft (4.88 m).(140) The test variables were fiber content (0, 1, and 2 percent by volume) and quantity of conventional nonprestressed reinforcement (0.00 to 1.00 percent by area). Measured compressive strengths of the UHPC ranged from 24.7 to 29.4 ksi (170 to 203 MPa).
Beams containing 1- and 2-percent fiber reinforcement had higher first cracking strengths, better post-cracking flexural response, and higher peak loads than beams without fibers. Increasing the fiber content from 1 to 2 percent resulted in stiffer post-cracking response and higher peak loads. The beams containing no fibers failed when flexure-shear cracks extended into the compression region under the load points, leading to a shear failure of the flexural compression block in the shear span. The beams containing the fibers failed when the fibers pulled out across a critical crack and the reinforcing bars ruptured. No concrete crushing was noted.
Visage et al. reported the results of ten 6-inch (152-mm)-square beams tested in flexure.(141) Test variables included compressive strength, amount of flexural reinforcement, volume of steel fibers, and beam length. Test results were compared with traditional methods ofestimating moment-curvature relationships. Other flexural tests have been reported by Gröger et al., Frettlöhr et al., and Stürwald and Fehling. (142,143,144)
Adeline and Behloul reported flexural tests of two 49.2-ft (15-m)-long UHPC beams containing only flexural reinforcement.(145) The beams contained eight or four 0.6-inch (15.2-mm)-diameter strands. The beam with eight strands failed by crushing of the UHPC, whereas the beam with two strands failed by strand rupture. Both beams exhibited large deflections before failure. The authors used a nonlinear multilayer program to predict the moment-deflection curves. They obtained very good agreement between the measured and calculated curves in both the elastic and plastic parts of the curves.
Maguire et al. tested two full-size double-tee beams in flexure.(146) The beams contained 0.7-inch (17.8 mm)-diameter strands and UHPC without steel fibers. The measured strengths exceeded the calculated strengths using measured properties and a strength design approach. The authors concluded that the flexural design procedures of the AASHTO LRFD Specifications for I-girders are applicable to UHPC girders.
Steinberg and Reeves examined the reliability of the flexural strength of UHPC AASHTO standard box beams based on the AASHTO LRFD Bridge Design Specifications.(147,148,149) The reliability analysis consisted of a Monte Carlo simulation and the use of the moment-curvature approach to calculate flexural strength. The authors concluded that the use of the AASHTO LRFD Specifications produces a conservative reliability index when applied to UHPC members. For lightly reinforced members, the design may be overly conservative. To rectify this, they suggested using a more advanced analysis method, such as moment-curvature, or increasing the strength reduction factor.
Prior to construction of Malaysia's first UHPC motorway bridge, a prototype I-girder was tested in flexure using a single point load at midspan. (150) The load-deflection curve predicted by finite element modeling matched the measured values very closely.
Sujivorakul developed a flexural model to predict the moment-curvature relationship for doubly reinforced UHPC beams.(151) The model is based on strain compatibility, equilibrium of forces, and the stress-strain relationship of UHPC in tension and compression.
For strength design, Stürwald and Fehling developed a simplified approach.(144) They used a triangular stress block in compression and a rectangular stress block for tension in the UHPC. This approach gave calculated strengths within 5 percent of the measured strength of three beams.
Walsh and Steinberg examined the moment redistribution capacity of four small-scale continuous two-span UHPC beams with no conventional reinforcement. (152) The test results suggested that the moment redistribution of UHPC is comparable to the 20-percent maximum given in the AASHTO LRFD Bridge Design Specifications.(76)
Tue et al. examined the capacity of stub columns of UHPC confined by a steel tube.(153) The load was applied either to the combined steel and UHPC section or to the UHPC section alone. The authors observed that shrinkage of the UHPC produced a gap between the UHPC and the inside of the steel tube. This gap only closed after the stresses exceeded the service level and lateral strains increased considerably. As such, the confinement effect was not as effective as that achieved with conventional concrete.
Empelmann et al. tested six short columns in concentric compression. The 7.9- by 7.9- by 23.6-inch (200- by 200- by 600-mm) columns contained different amounts of longitudinal and transverse reinforcement.(154)
Yan and Feng also tested short UHPC columns with a diameter of 4.3 inches (110 mm) inside steel tubes with a wall thickness of 0.19 to 0.26 inches (5 to 6.5 mm).(155) Measured compressive strengths were greater than calculated by the equation in figure 11.
![]()
Figure 11. Equation. Strength of columns
where:
fy = tensile yield strength of the steel tube
As = cross sectional area of the steel tube
f'c = compressive strength of 4-inch (100-mm) UHPC cubes
Ac = cross sectional area of the concrete
The authors noted that confinement of the steel tube was not as effective as that for conventional concrete, and therefore, the effect can be neglected in the calculation of axial load.
A method for measuring the uniaxial tensile stress-strain response has recently been developed by a U.S.–French joint project.(78) The test method provides the response for both precracking and post-cracking phases without requiring any complex stress or strain transformations.
Jungwirth and Muttoni reported the results of direct tension tests on dog-bone shaped specimens having a test cross section of 1.8 by 6.3 inches (45 by 160 mm).(156) They reported a linear stress-strain relationship with a modulus of elasticity of about 8,700 ksi (60 GPa) up to a tensile stress of 1.2 ksi (8.5 MPa). Following cracking of the specimens, the tensile stress increased to about 1.45 ksi (10 MPa) before the fibers progressively pulled out at a strain of about 2.5 percent. The authors also performed tests on specimens containing nonprestressed reinforcement ranging from 1 to 4.5 percent by area. All specimens exhibited well-distributed cracking and strains as high as 10 percent.
Further discussion of the tensile response of UHPC is provided in chapter 3 under the heading of tensile strength.
Holschemacher et al. investigated the bearing strength of two UHPCs, with and without helical reinforcement, using two different specimen heights and different diameters of loading area.(157,158) Results were compared with the German Standard DIN 1045-1.(159) The results indicated that the strengths calculated using DIN 1045-01 equations need to be modified by a factor such as 0.8 for them to be applicable to UHPC.
Hegger et al. tested various details for joints between precast UHPC columns.(160) The major test variables included dry and wet joints. With dry joints, the surface treatment of the interface surfaces and the longitudinal reinforcement ratio were variables. With wet joints, the mortar thickness and transverse reinforcement ratios with welded wire reinforcement and steel plates were variables. Measured bearing capacities were slightly less than measured on a continuous reference column.
The AASHTO LRFD shear design sectional model involves the calculation of three components that contribute to shear resistance. They are the concrete contribution, the transverse or shear reinforcement contribution, and any vertical component of prestressing force from draped strands. The procedure involves a combination of theory and empirical factors. In UHPC beams with no conventional transverse reinforcement, there is no reinforcement contribution. The tensile stresses that develop are carried by the UHPC matrix and steel fibers.
Graybeal tested three 36-inch (0.91-m)-deep AASHTO Type II prestressed UHPC girders in shear. The girders contained no nonprestressed shear reinforcement.(109) Each girder failed in a different manner. The first girder failed owing to a preexisting horizontal crack at the base of the web from a prior flexural test. The second girder failed owing to diagonal tension in the shear region. The third girder failed owing to a combination of diagonal tension and strand slip. Because the girders did not contain any nonprestressed shear reinforcement and no draped strands, Graybeal proposed that the shear capacity could be determined by assuming that all the shear forces are carried by diagonal tension and compression in the web of the girder. The limiting value is the post-cracking tensile strength of the UHPC. A conservative estimate of this value would be required. In addition, it is necessary to determine the state of stress in the girder under dead load and prestressing forces.
Graybeal also tested three 33-inch (838-mm)-deep pi-girders with shear spans of 7.0, 6.0, and 6.0 ft (2.13, 1.83, and 1.83 m) under three-point bending.(113) First, shear cracks appeared at shear loads of 175, 180, and 205 kips (780, 800, and 910 kN). The shear loads at failure were 430, 366, and 510 kips (1,910, 1,630, and 2270 kN). However, the third girder failed in flexure rather than loss of diagonal tensile capacity in the web as occurred in the first two girders. Based on an analysis in accordance with the AASHTO LRFD Bridge Design Specifications, a 70-ft (21.3-m)-span girder has a Service III shear demand of 103.2 kips (459 kN) and a Strength I shear demand of 206 kips (916 kN).(76) The measured shear strengths were at least 75 percent greater than the Strength I demand. Based on the assumption that the girder webs carried all the shear force and that the diagonal tensile force acted uniformly over the relevant cross-sectional area of the webs, the calculated diagonal tensile capacities corresponding to the shear loads at failure were 2.5, 2.1, and 2.9 ksi (17.2, 14.6, and 20.3 MPa) for the three girders.
Maguire et al. reported shear tests of two full-size double-tee beams.(146) The beams contained vertical shear reinforcement consisting of welded wire reinforcement with cross wires for anchorage. The UHPC did not contain any steel fibers. Both girders had a measured shear strength that exceeded the calculated shear strength based on measured material properties. The authors concluded that the AASHTO LRFD Bridge Design Specifications for shear design of I-girders is applicable to UHPC girders.(76)
Baby et al. reported on a study investigating the shear performance of UHPC beams.(163,164) Study variables included prestressed versus nonprestressed beams, the inclusion of stirrups for shear reinforcement, and the inclusion of fiber reinforcement. Supplemental beams were cast and then deconstructed to extract prismatic specimens from the web region for three-point bending tests. These small-scale tests provided an indication of the fiber reinforcement orientation and effectiveness as shear reinforcement in the web. Thisresearch found that the shear design recommendations contained within the SETRA-AFGC UHPFRC Design Guidelines were conservative for these beams. (4)
Shear tests of UHPC beams without conventional shear reinforcement were conducted by Bunje and Fehling.(165) All specimens failed in flexure. Other shear tests were conducted by Hegger et al., Hegger and Bertram, Cauberg et al., Fehling and Thiemicke, and Bertram and Hegger. (See references 166, 167, 168, 169, and 170.)
Hegger and Bertram tested 15.7-inch (400-mm)-deep prestressed concrete I-beams with a length of 185 inches (4.70 m).(167,171) Four series of beams were tested as follows:
The beams in the first three series did not contain any conventional transverse reinforcement.
For beams without openings, the shear strength increased as the fiber content increased. An increase in the prestressing force resulted in an increase in the shear strength. The provision of a single opening reduced the shear strength. However, the strengths of beams with two openings were similar to those of beams with a single opening.
Wu and Han reported tests of 11 reinforced concrete I-girders of which 8 failed in shear.(172) The main variables were fiber volume content, flexural reinforcing steel ratio, section type, and span/ depth ratio. No shear reinforcement was provided in the webs. Based on the test results, a formula for the first diagonal cracking load was developed. The authors concluded that the conventional equations for calculating shear strength are not appropriate and developed an analytical model.
Prior to construction of Malaysia's first UHPC motorway bridge, a prototype I-girder was tested in shear using a single point load at midspan. (150) No conventional shear reinforcement was included. The shear strength predicted by finite element modeling was 17 percent lower than the measured strength.
Section 9 of the AASHTO LRFD Bridge Design Specifications requires a minimum deck thickness of 7.0 inches (175 mm) unless approved otherwise by the owner.(76) This generally precludes the likelihood of a punching shear failure in a bridge deck. The use of thinner sections with UHPC increases the likelihood of a punching shear failure and, therefore, the need to consider it in design.
Harris and Roberts-Wollmann tested twelve 45-inch (1,140-mm)-square UHPC slabs in punching shear.(173,174) The variables in the program were slab thicknesses of 2.0, 2.5, and 3.0 inches (51, 64, and 76 mm) and loading plate dimensions from 1.0 to 3.0 inches (25 to 76 mm) square. No conventional reinforcement was included. The measured compressive strength of the UHPC was 32.1 ksi (221 MPa). Seven of the specimens failed in punching shear and five in flexure. The authors concluded that the American Concrete Institute (ACI) 318 equation forpunching shear predicted the failure loads reasonably well but a modified version of the ACI model for breakout loads provided the best prediction. (162) They also concluded that a 1.0-inch (25-mm) slab thickness should provide sufficient thickness to resist punching shear in bridge deck applications.
Three larger slabs with dimensions of 7.0 by 12.0 ft and 3 inches thick (2.1 by 3.7 m by 76 mm) were loaded with a wheel patch load. These tests represented the top flange of a double-tee section. The slabs all failed in tension.
Toutlemonde et al. investigated the local bending and punching shear performance of two-way ribbed bridge deck elements.(175) Developed as a potential alternate for orthotropic bridge decks, these 15-inch (0.38-m)-deep deck elements were composed of a 2-inch (0.05-m)-thick plate and 13-inch (0.33-m)-tall bi-directional ribs with a 24-inch (0.6-m) center-to-center spacing. This study tested two different commercially available UHPC products. The punching shear capacity of the deck plate was observed to be greater than 157 kips (700 kN) under all conventional loading scenarios. When the wheel patch was reduced to a 7.5 x 10.2 inch (0.19 x 0.26 m) size, the authors observed the punching shear resistance to be between 79 and 94 kips (350 and 420 kN).
Naaman et al. evaluated the effect of fibers on the punching shear response of 7-inch (175-mm)-thick concrete bridge decks with and without reinforcing bars.(176) Three different types of fibers were included. Test results showed that the punching shear resistance, the energy-absorption capacity, and the resistance to spalling of slabs having only two bottom layers of reinforcing bars were significantly better than for the control specimen with four layers of reinforcing bars and conventional concrete. The authors concluded that punching shear resistance can be safely taken as twice that calculated using the procedures of ACI 318-05.(177)
Saleem et al. tested eight single-tee, simple span beams with a depth of 5 inches (125 mm), a top flange width of 12 inches (300 mm), and a span length of 48 inches (1219 mm).(178) A center point load was applied over an area 19.7 inches (500 mm) long by 9.8 inches (250 mm) wide, representing an AASHTO HS20 truck dual tire wheel. All beams contained longitudinal flexural reinforcement but only two beams had shear reinforcement. The dominant mode of failure in the beams was shear.
Aaleti et al. reported punching shear tests on the 8-inch (200-mm)-deep waffle slab system proposed for use on a bridge deck in Iowa.(179) They concluded that the system would not experience punching shear failure under the traditional 10 by 20 inch (254 by 508 mm) wheel loads. The measured punching shear strength was nearly 2.3 times the estimated value using the ACI equation recommended by Harris and Roberts-Wollmann.(174)
Punching shear tests were reported by Joh et al.(107) Tests were made on 63-inch (1,600-mm)-square slabs with thicknesses of 1.6 and 2.8 inches (40 and 70 mm) and loaded through plates with dimensions of 2.0 by 2.0, 3.0, 3.9, or 4.9 inches (50 by 50, 75, 100, or 125 mm). The 1.6-inch (40-mm)-thick slabs reached their flexural strength before punching occurred. The 2.8-inch (70-mm)-thick slabs failed by typical punching at the center of the slab. The authors confirmed that the ACI 318 equation for punching shear gave a reasonable estimate of the strength.
Bunje and Fehling conducted punching shear tests of UHPC slabs with thicknesses of 1.2, 1.6, 2.0, and 3.1 inches (30, 40, 50, and 80 mm).(165) The slabs did not appear to contain any conventional flexural reinforcement. All slabs failed in a ductile flexural mode with no punching failure.
Moreillon et al. reported punching shear tests in which the primary variables were slab thickness, reinforcement ratio, and fiber volume.(180) The authors developed a model for predicting the punching shear strength.
Twenty-four push-off tests were conducted by Banta to determine whether the horizontal shear design equations of the AASHTO LRFD Bridge Design Specifications accurately predict the horizontal shear strength between UHPC and lightweight concrete.(181) The test variables were interface surface characteristics, interface area, and area of reinforcement crossing the interface. The author compared the test results of 19 specimens with a smooth interface with the equations in the 2004 version of the Specifications, assuming a resistance factor of 1.0 and a friction factor of 1.0.(182) Calculated strengths were always greater than measured strengths. It should be noted that the cohesion and friction factors have been revised since publication of the 2004 version of the LRFD Specifications.
Maguire et al. cautioned that the contribution of the contact surface between precast UHPC girders and a cast-in-place conventional concrete deck should be ignored because of the difficulty of roughening the top surface of the UHPC girders.(146)
Crane and Kahn investigated the interface shear capacity of five reinforced tee beams with UHPC for the web and high-performance concrete (HPC) for the top flange.(183) Test variables included interface roughness and amount of interface shear reinforcement. Test results were compared with the shear friction equations of the AASHTO LRFD Bridge Design Specifications. The equations were unconservative in predicting the shear strength of smooth interfaces even with relatively high amounts of shear reinforcement. Consequently, it was recommended that a fluted interface be used.
Hegger et al. conducted direct shear tests on joints between precast elements subjected to various levels of compression.(160) They included dry and wet joints with various types of contact surfaces.
Graybeal evaluated the use of UHPC in shear connectors between precast deck panels and concrete or steel beams.(184) He tested two full-size beam specimens. The first specimen included frequently implemented details used to connect precast concrete slabs to beams. Conventional grout was used. The second specimen used simplified connection details in combination with UHPC. The tested UHPC connections eliminated all interference points between the girder and deck connectors by engaging the mechanical strength of the UHPC to carry the loads between the connectors across an otherwise unreinforced plane. Each specimen was subjected to more than 11 million cycles of loading followed by a static test to failure. The applied loads surpassed the design loads required by the AASHTO LRFD Bridge Design Specifications.(76) The author observed no damage in the UHPC connections after they were subjected to 168 psi (1.16 MPa) of cyclic horizontal shear stress and 789 psi (5.44 MPa) of static horizontal shear stress along the minimum shear plane.
Hegger et al. have tested headed stud and continuous shear connectors using push-off tests and a beam test.(185,186,187) The test parameters for the continuous connector push-off tests were steel fiber content, transverse reinforcement ratio, and thickness of the connector. The amount of steel fibers had a minor effect on the connector strength if a minimum fiber ratio was maintained. The arrangement of transverse reinforcement influenced the connector strength, whereas the thickness of the connector influenced strength and the mode of failure. In the beam test, the plastic moment was developed with no cracks developing at the connector.
Jungwirth et al. and Kohlmeyer et al. also conducted push-off tests of continuous shear connectors.(188,189)
Fehling and Ismail tested 7-inch (180-mm)-square beams in pure torsion.(190) The parameters included steel fiber type, steel fiber volume, longitudinal reinforcement ratio, and web reinforcement ratio. The use of longitudinal and transverse reinforcement in combination with the steel fibers provided the biggest increase in ultimate torsion capacity and ductility.
Joh tested three 12-inch (300-mm)-square beams in pure torsion.(191) One beam contained no conventional reinforcement, one beam contained longitudinal reinforcement in the corners, and the third beam contained both longitudinal and transverse reinforcement. The cracking torque and torsional strength were reasonably predicted using thin-walled tube theory modified to account for the tensile strength of the UHPC.
Empelmann and Oettel conducted tests on seven 20-inch (500-mm)-square hollow boxes with a wall thickness of 2 inches (50 mm) at midlength.(192) Test variables included fiber content, longitudinal reinforcement ratio, and transverse reinforcement ratio. Four specimens were loaded in pure torsion. Three specimens were loaded with a combination of torsion and axial force. The experimental results were compared with design equations for conventional concrete members based on a space truss model.
No recommendations about stress limits to be used in UHPC prestressed concrete members were identified. However, Graybeal reported high creep oncylinders loaded to between 60 and 92 percent of the compressive strength at compressive strength levels between 8.5 and 12.5 ksi (59 and 86 MPa). (22)
Loss of prestressing force includes an instantaneous loss when the strands are released and a time-dependent loss caused by creep and shrinkage of the concrete and relaxation of the prestressing strands. A reasonable estimate of the instantaneous loss can be made if the modulus of elasticity of theUHPC is known accurately. The AASHTO LRFD specifications provides two methods for predicting time-dependent losses:(76)
Both estimates rely heavily on empirical methods. The applicability of these methods for use with UHPC needs to be verified because this study identified no direct methods to measure prestress losses in UHPC.
Calculated prestress losses for Type II AASHTO girder based on material property tests were 35.6 ksi (245 MPa).(109) This included 15.4 ksi (106 MPa) for instantaneous loss, 10.0 ksi (69 MPa) for shrinkage, 6.9 ksi (48 MPa) for creep, and 3.1 ksi (21 MPa) for relaxation.
Article 5.10 of the AASHTO LRFD Bridge Design Specifications addresses reinforcement details.(76) No specific publications addressing these details for use with UHPC were identified. It is likely, however, that most of these provisions could be used with UHPC because of UHPC's higher compressive and tensile strengths.
New York State Department of Transportation performed pullout tests of No. 4, 5, and 6 bars embedded 2.9, 3.9, and 4.9 inches (75, 100, and 125 mm),respectively, in 15.7-inch (400-mm)-diameter UHPC cylinders, which resulted in reinforcement fracture within the length of bar not cast into the UHPC. (193)
Graybeal and Swenty conducted pullout tests on No. 4 reinforcing bars embedded into 6-inch (152-mm) cubes of two different UHPCs.(194) The rebar was bonded to the field-cast UHPC for 3 inches only, with the remainder of the length debonded by a foam bond-breaker. All of the specimens were cast and cured in ambient laboratory conditions. Pullout tests on a UHPC formulation intended for use in precast concrete applications resulted in pullout of the bar after the tensile yield strength of the bar had been surpassed. Pullout tests on a UHPC formulation intended for field-cast applications resulted in tensile rupture of the reinforcement.
Pullout tests were also performed by Holschemacher et al. using 0.32- and 0.39-inch (8- and 10-mm)-diameter bars.(195,196) They observed that the bond strength and stiffness increased with testing ages. Fehling et al. also performed pullout tests on 0.47-inch (12-mm)-diameter bars with various amounts of concrete cover and embedment lengths.(197)
Hossain et al. completed pullout and development length tests of glass fiber reinforced polymer (GFRP) rebar embedded in two different UHPC formulations.(198) Both No. 5 and 6 bars were tested with both high and low modulus of elasticity GFRP formulations. Larger bars and longer bond lengths were observed to result in lesser bond strengths, with all specimens failing via bar pullout.
No publications about the development length of deformed bars in compression in UHPC were identified.
Graybeal evaluated the performance of six connection details for use between precast concrete elements.(193,199) Four connections represented transverse joints between full-depth precast concrete deck panels. Two connections represented longitudinal joints between adjacent deck bulb-tee girders. Table 10 provides the reinforcement details used in the connection regions. Bars from adjacent panels were offset by half the bar spacing.
| Orientation | Bar Size | Bar Type | Lap Length, inches | Bar Spacing, inches | |
|---|---|---|---|---|---|
| Top | Bottom | ||||
| Transverse | No. 5 | Headed uncoated | 3.5 | 17.7 | 7.1 |
| Transverse | No. 4 | Hairpin epoxy coated | 3.9 | 4.3 | 4.3 |
| Transverse | No. 5 | Straight galvanized | 5.9 | 17.7 | 7.1 |
| Transverse | No. 5 | Straight uncoated | 5.9 | 17.7 | 7.1 |
| Longitudinal | No. 5 | Headed uncoated | 3.5 | 17.7 | 7.1 |
| Longitudinal | No. 5 | Straight uncoated | 5.9 | 17.7 | 7.1 |
| 1 inch = 25.4 mm | |||||
The specimens were loaded on a simple span, with the load applied through a simulated wheel patch placed adjacent to the connection near midspan. Cyclic loads were applied first, with the test program including at least 2 million cycles to a load just below the cracking strength of the specimen followed by at least 5 million cycles to a load larger than the cracking strength of the specimen. After the completion of the cyclic testing, each test specimen was statically loaded to failure. All the specimens survived 7 million cycles of fatigue loading.
The tests showed that noncontact, lap-spliced reinforcement in the transverse and longitudinal connections was not susceptible to debonding under cyclic and static loads. The development length of straight, uncoated No. 5 reinforcing bars in this test program was demonstrated to be equal to or less than 5.9 inches (150 mm) in a non-contact lap splice configuration.
Hegger et al. reported on direct tension tests of lap-spliced specimens.(160) The test variables were bar diameter, lap length, steel fiber ratio, transverse reinforcement ratio, and concrete cover.
Hossain et al. reported on testing lap-spliced GFRP rebar in field-cast connections between prefabricated bridge deck elements.(198) This testing, which included both static and cyclic flexural loading of the beam splice connections, demonstrated that 5.9- to 8.9-inch (150- to 225-mm) lap splice lengths can be appropriate for GFRP rebar embedded in UHPC.
No publications about the development length of standard hooks in tension in UHPC were identified. However, it is likely that the existing provisionsof the AASHTO LRFD Bridge Design Specifications are applicable because of UHPC's higher compressive and tensile strengths.(76)
No publications about the development length of welded wire reinforcement in UHPC were identified. However, it is likely that the existing provisionsof the AASHTO LRFD Bridge Design Specifications are applicable because of UHPC's higher compressive and tensile strengths.(76)
No publications about the development length of shear reinforcement in UHPC were identified. However, it is likely that the existing provisions of theAASHTO LRFD Bridge Design Specifications are applicable because of UHPC's higher compressive and tensile strengths.(76)
Measured transfer and development lengths from various researchers are summarized in table 11.
| Strand Diameter | Transfer Length | Development Length | Source | |||
|---|---|---|---|---|---|---|
| inches | mm | inches | mm | inches | mm | |
| 0.6 | 15.2 | 14 | 356 | < 35 | < 890 | Ruiz et al.(200,201) |
| 0.5 | 12.7 | 8.7 to 11.0 | 220 to 280 | — | — | Bertram and Hegger(202) |
| 0.7 | 17.8 | 17 to 21 | 430 to 530 | — | — | Maguire et al.(146) |
| 0.5 | 12.7 | — | — | < 37 | < 940 | Graybeal(109) |
| — No data reported. | ||||||
Graybeal reported results of a study investigating the lap-splice length of unstressed prestressing strands.(203) Strands were lapped inside UHPC prisms and then loaded in direct tension. Strand rupture failures indicated that that lap length for 0.5-inch (12.7-mm)-diameter strands is approximately 18 inches (457 mm), and the lap length for 0.6-inch (15.2-mm)-diameter strands is approximately 26 inches (660 mm).
Steinberg and Lubbers reported the results of pullout tests of 0.5-inch (12.7-mm)-diameter standard and oversize prestressing strands embedded 12, 18, and 24 inches (305, 457, and 610 mm) in UHPC.(204,205) In comparison with conventional concrete having compressive strengths less than 4.0 ksi (28 MPa), the UHPC had higher bond strengths. The results indicated that the strand strength was developed in less than 12 inches (25.4 mm).
Based on tests with 0.5-inch (12.7-mm)-diameter seven-wire strands, Hegger et al. showed that the minimum cover and minimum clear spacing to prevent splitting in UHPC could be reduced to 1.5d and 2.0d where d is the strand diameter.(166) This is less than required by the German DIN 1045-01 for conventional concrete.(159) In other tests, a concrete cover less than 2.5d led to splitting cracks.(206) The authors recommended a minimum cover of 2.5d and a minimum clear spacing of 2.0d.(202)
Chen and Graybeal reported the results of a research program to develop finite element analysis modeling techniques applicable to UHPC structural components.(207) The mechanical properties used in the modeling are given in table 12.
Results of the analysis using the values given in table 12 compared favorably with values measured during tests on an I-girder and a pi-girder. (208,209)
| Value | ||
|---|---|---|
| Property | English Units | Metric Units |
| Unit Weight | 160 lb/ft2 | 2,565 kg/m2 |
| Compressive Strength | 29 ksi | 200 MPa |
| Modulus of Elasticity | 7,650 to 8,000 ksi | 53 to 55 GPa |
| Poisson's Ratio | 0.18 | 0.18 |
| Post-Cracking Tensile Strength | 1.4 to 2.3 ksi | 9.7 to 15.9 MPa |
| Ultimate Tensile Strain | 0.007 to 0.010 | 0.007 to 0.010 |
The literature search identified the following national recommendations for UHPC:
On a more global scale, the Fédération Internationale du Béton (fib) Task Group 8.6 is developing recommendations tailored to the design ofUHPC structures.(211) The table of contents of the draft version have been published in Walraven.(211)
The Australian guidelines were developed for the design of prestressed concrete beams manufactured using Ductal®.(210) Where possible, a limit state approach consistent with the design requirements of the Australian Standard for Concrete Structures AS3600-1994 was adopted.(212) The design procedures are based on the principles of structural mechanics and the material properties and behavior reported in the literature. Design guidelines are provided for strength, serviceability, and durability.
The material design properties address behavior in compression and tension, modulus of elasticity, density, Poisson's ratio, creep, and shrinkage. Design guidelines are provided for strength in flexure, strength in shear, strength in torsion, flexural crack control at service loads, deflection at service loads, loss of prestress, and anchorage zones.
Theoretical flexural capacity is based on equilibrium of forces and strain compatibility using idealized stress-strain curves in compression and tension for UHPC. A strength reduction factor of 0.8 is used for sections containing bonded reinforcement and 0.7 for sections containing no bonded reinforcement. Ductility is provided by limiting the ratio of neutral axis depth to effective depth to a maximum value of 0.4.
Shear strength of the UHPC in beams is based on limiting the principal tensile stress at the centroidal axis or at the junction of the web and flange to a maximum value based on a section uncracked in flexure. This maximum value is provided in figure 12. When beams contain stirrups or inclined tendons, their contribution to shear resistance may be included in the same way as conventional reinforced concrete design. An equation is provided for the punching shear strength.
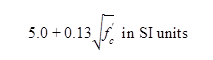
Figure 12. Equation. Shear strength of UHPC beams(210)
The torsional strength, for a member not containing torsional reinforcement, is taken as the pure torsion required to cause first cracking.
Flexural cracking is controlled by limiting the maximum tensile stress to 870 psi (6.0 MPa) in nonprestressed elements and 1,160 psi (8.0 MPa) in prestressed elements.
Short-term deflections are calculated using conventional procedures for uncracked sections and integration of curvatures for cracked sections. Long-term deflection calculations are based on an age-adjusted effective modulus.
The guidelines suggest that a reliable estimate of prestress losses can be obtained using the age-adjusted effective modulus.
The transfer length of prestressing strands is to be taken between 20dband 40dbdepending on the stress condition being analyzed, where db is the strand diameter.
Appendices to the guidelines provide design examples.
This document could provide a template for a similar set of guidelines based on the AASHTO LRFD Bridge Design Specifications.(76)
The draft recommendations in Recommendations for Design and Construction of Ultra High Strength Fiber Reinforced Concrete Structures (Draft), published by the Japan Society of Civil Engineers in 2006, provide basic principles for design and construction using UHPC.(8) The design values for materials include compressive strength, first cracking strength, tensile strength, stress-strain relationships, modulus of elasticity, Poisson's ratio, thermal characteristics, shrinkage, creep, and fatigue. Other chapters address structural safety (strength design), serviceability, fatigue resistance, structural details, prestressed concrete, durability, construction (constituent materials, mix proportions, production, transportation, and inspection), cold-weather concreting, and hot weather concreting. The recommendations build on the Standard Specifications for Concrete Structures prepared by the Japanese Society of Civil Engineers.(213) Both recommendations and extensive commentary are provided.
For flexural design, the use of stress-strain curves rather than an equivalent stress block is recommended. No minimum amount of steel reinforcement is required because the bridging action of the steel fibers provides the strength after cracking.
Shear capacity is calculated as the summation of the shear resistance provided by the matrix, fiber reinforcement, and vertical component of the prestressing force or the shear resistance to diagonal compression failure. The use of shear reinforcement is not recommended. Torsional design is based on the Society's Standard Specifications. An equation is provided for the calculation of punching shear strength.
Serviceability is addressed by checks on stresses, displacements, deformations, vibrations, and other parameters as needed. Verification of fatigue resistance relies on the provisions of the Standard Specifications.
In pretensioned concrete, the clear vertical or horizontal distance between strands may be equal to the strand diameter. A minimum clear cover of 0.8 inches (20 mm) is permitted.
Overall, the document is comprehensive, although it defaults to the Standard Specifications where information is not available to develop different recommendations for UHPC.
The French recommendations are composed of three parts.(4) The first part provides specifications regarding the mechanical properties to be obtained, procedures to be used for placement, and checks and inspection during construction and of the finished product. The second part deals with the design and analysis of UHPC structures and accounts for the participation of fibers, nonprestressed reinforcement, and non-reinforced elements. The third part deals with durability of UHPC.
The first part provides design information for compressive strength, tensile strength, modulus of elasticity, Poisson's ratio, coefficient of thermal expansion, shrinkage, creep, and impact behavior. Mix design, mixing procedures, placement practices, and tests are addressed.
The design methods in the second part are based on the French codes for prestressed and reinforced concrete but take into account the strength provided by the fibers. The recommendations include an orientation coefficient that accounts for the alignment of fibers that may occur during placement. A minimum fiber content and non-brittleness check is also required. The stresses at the serviceability limit state are addressed in the same way as conventional reinforced or prestressed structures. When no prestressing steel or nonprestressed reinforcement is provided, a crack width criterion is used.
For the ultimate flexural strength limit state, the recommendations propose a stress-strain relationship that is linear for the compressive stress range but multilinear in the tensile stress range to account for the effect of the fibers.
At the serviceability limit state for shear, the recommendations use the shear stress limits of the French Code for prestressed concrete. Shear strength is calculated as the summation of the shear resistances provided by the concrete, reinforcement, and fibers.
The components of the third part address water porosity, oxygen permeability, chloride ion diffusion, portlandite content, stability of admixtures, delayed hydration, corrosion of steel fibers, and durability of polymer fibers.
More details on specific topics are provided in nine appendices. Feedback and research resulting from the use of the French recommendations have been summarized by Resplendino.(214)
Limited testing under flexural or axial loads indicates that the flexural and axial strengths of UHPC members can be calculated with reasonable accuracy if the stress-strain relationships of UHPC are included in the analyses. However, the calculations are more complex than using the simplified approach of a rectangular compressive stress block and zero tensile strength.
The shear strength of UHPC beams containing conventional shear reinforcement and no steel fibers can be predicted using the sectional design method of the AASHTO LRFD Bridge Design Specifications.(76) For UHPC beams with steel fibers and without conventional shear reinforcement, a strength calculation based on the maximum principal tensile stress has been used.
Where design for punching shear is required, the equations in ACI 318 may be used.(162) For shear friction, the available test results need to be compared with the existing specifications.
The limited information available on torsion tests indicates that design could be performed using traditional mechanics of materials approach and limiting the maximum principal tensile stress.
For prestressed concrete, no stress limits or prestress loss values have been established for UHPC. The limited information on transfer length and development length of prestressing strand indicates that the lengths are much shorter in UHPC than in conventional concrete. Similarly, development lengths for deformed bars in tension and lap splices in tension are shorter than for conventional concrete.
For prestress losses, approximate estimates can be made using the modulus of elasticity, creep, and shrinkage data summarized in chapter 3.
Information on reinforcement details, standard hooks in tension, and development of welded wire reinforcement and shear reinforcement in UHPC members was not identified.
Three countries have developed design guidelines for use with UHPC. Although these documents are not as complete as the AASHTO LRFD Bridge Design Specifications, they do address the major design requirements.(76)