U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-16-055 Date: January 2016 |
Publication Number: FHWA-HRT-16-055 Date: January 2016 |
This section describes in detail the methodology embedded in the TIM-BC tool. First, the section presents the selected TIM strategies according to surveys from the project advisory committee. It then addresses the development of a duration/proportion-based estimation (D/P-E) method to enable the comparison of traffic performance before and after the implementation of TIM strategies. A simulation-based evaluation approach is presented to calibrate regression models and populate lookup tables to predict travel delays, fuel consumption, emissions, and secondary incidents. Finally, methods to evaluate benefits and costs of selected TIM strategies are proposed.
Various types of TIM strategies have been implemented worldwide. Due to the constraints of time and budget, a project advisory committee was interviewed regarding which TIM strategies they use at their agencies. The strategies were then ranked from highest to lowest based on the percentage of respondents’ agencies that use that strategy. Eight TIM strategies that are most widely adopted and considered most effective were selected for the new TIM-BC tool, as shown in table 4.
| TIM Strategy | Description |
|---|---|
| Safety Service Patrols (SSP) | SSPs provides short-term traffic control and scene management along interstate highways and controlled-access primary routes, reducing incident duration and promoting the safe movement of people and commerce. |
| Driver Removal Laws (DRL) | Driver removal laws require or encourage drivers whose vehicles are involved in a traffic incident to move their vehicles from the road when they are able to do so. |
| Authority Removal Laws (ARL) | Authority removal laws give TIM responders some measure of authority to have vehicles, debris, and spilled cargo removed from the road when the owners are unwilling or otherwise unable to do so in a timely manner. |
| Shared Quick-Clearance Goals (SQCG) | Some TIM management areas with coordinated, interdisciplinary TIM response structures adopt shared quick-clearance goals to improve clearance time across all incident types. |
| Preestablished Towing Service Agreements (PTSA) | Preestablished towing service agreements between TIM management agencies and local towing services promote, via contractual obligation, the level of service that those companies must provide. These obligations are usually set in terms of availability and response times of towing vehicles. |
| Dispatch Collocation (DC) | Collocation of dispatch personnel and equipment can improve communication between responders, thus decreasing dispatch and initial response times. |
| TIM Task Forces (TTF) | TTFs are groups of TIM-related planners, managers, and other personnel that meet periodically to coordinate activities and policies. |
| Second Strategic Highway Research Program (SHRP2) Training (ST) | SHRP2 National Traffic Incident Management Responder Training. SHRP2 training focuses on motorist and responder safety while minimizing impact to traffic flows. |
The interviews with the project advisory committee also concluded that the new TIM-BC tool should mitigate many of the gaps identified in the other tools, leading to the following requirements (R1, R2, R3):
R1. The tool should be able to account for multiple TIM strategies with consistent methods.
R2. The tool should account for both direct and indirect benefits.
R3. The tool should be presented with a postprocessing, user-friendly interface and require relatively simple data inputs from the user.
In response to these requirements, this study proposes the following three solutions (S1, S2, S3), which will be detailed in the remainder of this report.
S1. The proposed BC estimation method, referred to as D/P-E, is suitable for the evaluation of all selected programs and applied consistently across eight subtools.
S2. The developed evaluation methodology adopts simulation and statistical analysis techniques introduced by TariVerdi(11) and Miller-Hooks et al.(12) to be able to estimate the savings caused by any TIM program in terms of travel delay (cars and trucks), fuel consumption, emissions, and secondary incidents.
S3. The developed tool is a user-friendly and easy-to-access Web-based tool that consists of multiple convenient functions, such as segment cloning, to avoid repetitive data entries by users. Input data requirements are low and only the most basic data that can be conveniently obtained are required, including general roadway geometry, incidents, traffic volume, composition, and general weather condition. Updatable monetary conversion factors are obtained from the latest identified, publically available database and embedded in the tool itself.
At the core of the developed TIM-BC methodology is an approach referred to as Duration/Proportion-based Estimation (D/P-E). This approach is based on the assumption that the benefits of TIM strategies, including travel delay, fuel consumption, emissions, and safety originate from the duration reduction of all or a proportion of incidents because of the TIM program. The three key parameters of this approach include:
These parameters need to be supplied by the users based on local conditions and engineering judgment. The tool provided default values to facilitate quick TIM evaluation, particularly for areas where targeted TIM programs have not been implemented and no relevant data are available. The most important parameters of the methodology are incident-duration savings.
For SSP programs, there are data available from different agencies. A study of the evaluation of the SSP program in Los Angeles assumed that the SSPs would reduce incident duration by 10, 12.5, or 15 minutes, resulting in a B/C ratio that ranged from 3.75:1 to 5.5:1.(28) Moreover, the average duration of crashes and in-lane incidents handled with the Hoosier Helper SSP program were assumed to be lowered by 10 minutes while all other incident durations were reduced by 15 minutes.(29) Chou et al.(10) lengthened the duration of incidents without FSP assist incidents by between 5 and 25 minutes in 5-minute increments for studies on the SSP program of New York State, H.E.L.P. (Highway Emergency Local Patrol).They obtained results from statistical analysis of system data that are consistent with recommended values by the project committee during the interviews. Therefore, an average of 20 minutes for duration savings of the SSP programs was suggested in the TIM-BC tool as a default value. These values vary by program and roadway; local values should be used if available. However, no studies have been found to evaluate the duration savings for other strategies based on real-world data. Therefore, these values were obtained from the second round of interviews with the project advisory committee, as shown in table 5.
Information on other key parameters, such as the proportion of incidents that can be affected and the types of lane blockage that are applicable to different TIM strategies, were also obtained from the interviews, as shown in table 2. These values should be cautiously used, and when data are available, local values should be used to replace these default values.
| TIM Strategy | Methodology | DefaultParameter Values |
|---|---|---|
| Safety Service Patrol (SSP) |
Duration-based |
|
| Shared Quick-Clearance Goals (SQCG) Preestablished Towing Service Agreements (PTSA) Dispatch Collocation (DC) TIM Task Forces (TTF) SHRP2 Training (ST) |
Duration-based and proportion-based |
|
| Driver Removal Laws (DRL) Authority Removal Laws (ARL) |
Duration-based and proportion-based, with hypothetical incidents |
|
a After implementing DRL and ARL, the duration of incidents in the general lanes are reduced to 5 minutes. After vehicles moved to the shoulder, these incidents are processed and are referred to as shoulder incidents.
The methodologies for the selected eight TIM programs are categorized into three types, as shown in table 5. Based on the interview findings, it is recommended that a pure duration-based approach may be applied to SSP program analyses because it has the potential to reduce incident duration of almost all incidents. Users enter average duration savings or duration savings by lane blockage if available. Programs such as SQCG, PTSA, DC, TTF, and ST can also reduce incident duration but only apply to a proportion of incidents, and therefore a combined Duration and Proportion estimation method is applied. Users should enter average duration savings, percentage of applicable cases, and actual successful implementation rate.
DRL and ARL move a proportion of incidents from general lanes to the shoulder lane, and these incidents then become shoulder incidents after the removal. The impact of the new/hypothetical shoulder incidents on traffic should also be considered. Therefore, in addition to the combined Duration and Proportion estimation, hypothetical shoulder incidents are considered, and the amount of hypothetical shoulder incidents are set identically to the removed incidents from general lanes.
Users should enter the average shortened incident duration percentage of applicable cases and actual successful implementation rate. Note that the duration of hypothetical shoulder incidents is assumed to be the value obtained by subtracting shortened incident duration from the original general lane incident duration.
The following examples illustrate the concepts. Additional examples of selected TIM strategies are provided in appendix B.
Assumption
During the AM peak time period, there are 25 shoulder incidents with an average duration of 30 minutes, 20 one-lane incidents with an average duration of 35 minutes, and 10 two-lane incidents with an average duration of 45 minutes for the study period. Three scenarios for each of the three method categories in table 2 are provided next.
Scenario 1: SSP
Since the SSP applies to all entered incidents (since the tool requests inputs of the number of incidents to which only SSP vehicles have responded), with suggested average incident duration of 20 minutes, after the implementation, there are 25 shoulder incidents with a duration of 10 minutes (30 – 20 = 10), 20 one-lane incidents with a duration of 15 minutes (35 – 20 = 15) and 10 two-lane incidents with a duration of 25 minutes (45 – 20 = 25).
Scenario 2: DC
Since the DC applies to two-lane blockage incidents, after the implementation, there are 25 shoulder incidents with a duration of 30 minutes (no change), 20 one-lane incidents with a duration of 35 minutes (no change), and 10 two-lane incidents with a duration of 40 minutes (45 – 5 = 40).
Scenario 3: DRL
Since DRL applies to one-lane blockage incidents with assumed applicable proportion of 50 percent and a compliance rate of 30 percent, the duration of half (10) of the one-lane blockage incidents could be reduced (i.e. driver removal is possible) to 5 minutes as a result of driver removal. Of these incidents, 30 percent are assumed to be cleared by compliant drivers. After the implementation, there are 17 (20 – 3 = 17) one-lane blockage incidents with a duration of 35 minutes, 3 (0 + 3 = 3) one-lane incidents with a duration of 5 minutes, that are then moved to the shoulder, 25 shoulder incidents with a duration of 30 minutes (unchanged), and 3 (0 + 3 = 3) hypothetical shoulder incidents with duration of 30 minutes (35 – 5 = 30).
The simulation experiments were conducted using VISSIM (from "Verkehr In Städten – SIMulationsmodell" – German for "Traffic in cities – simulation model") microscopic traffic flow simulation (henceforth microsimulation) modeling platform.
As with other microsimulation models, VISSIM replicates individual movements of vehicles that make up the traffic composition, including personal cars, light- and heavy-duty trucks, motorcycles and transit vehicles, and related driver decisions. The properties of the different vehicle classes in terms of weight, power, and acceleration/deceleration rates were incorporated. In addition, driver behavior, including lane-changing behavior and other aspects of aggressiveness, was captured through the use of car-following models. Thus, simulation runs replicated the individual vehicle movements based on desired speeds, traffic volumes, vehicle and driver characteristics, interactions between the various entities, and interactions between these entities and the physical environment (i.e. roadway geometry).
In this study, traffic conditions surrounding incidents were replicated as well. Incident duration, number of lanes blocked, and other features were modeled. Their impacts on traffic in terms of driver response (e.g., rubbernecking) and induced delays due to, for example, the created shock wave and reduced roadway capacity were simulated.
To support the development of the models, various input data elements were required. This input includes:
To conduct the large number of needed simulation runs, the component object module (COM) interface of VISSIM was employed. The COM interface allows a modeler to access VISSIM objects (e.g., an individual vehicle) and control factors used in the underlying computational methods through a scripting language. Visual Basic was employed using this COM interface to develop codes that support batch runs in which input data—i.e., traffic conditions surrounding incidents—were varied. Thus, different incident scenarios were replicated in an automated manner.
Each VISSIM simulation under a given incident scenario produced outputs for specific BC estimates. In this effort, estimates of total travel delay (i.e., the difference between total travel time at free-flow speeds and realized total travel time as shown in equation 1) and fuel consumption were needed. VISSIM provides an estimate of total travel delay by vehicle class (specifically, passenger vehicles or heavy-duty trucks in this study) as an output. This estimate is based on the equation in figure 1. Thus, from each scenario, a single value of total travel delay per vehicle class was reported.
![]()
Figure 1. Equation. Total travel delay calculation.
where
D = total travel delay.
i = vehicle index.
t = time index.
uit = desired speed by vehicle i at time tvit = actual simulated speed of vehicle i at time t.
Δt = 1/number of time steps per simulation second (0.2).
Pollutant emissions were also estimated based on fuel consumption estimates, which were computed through previously developed fuel consumption estimation techniques, since it was found in earlier work that VISSIM does not reliably estimate fuel consumption. Details of this technique can be found in Miller-Hooks, et al.(30) The developed technique accounts for vehicle characteristics, such as weight and power, and the effects of roadway grade. This estimation technique requires second-by-second vehicle speed and acceleration profiles as input.
From each simulation run, two files were created: one file includes the total travel delay estimation and the other, significantly larger file contains the second-by-second speed and acceleration profiles, which are used for fuel consumption estimation.
The output from the analysis of an individual output file containing the speeds and accelerations is a single value of total fuel consumption for the given incident scenario. The estimated total travel times and total fuel consumption were collected in a single Microsoft® Excel file to develop fuel consumption estimation regression models for use in the overall benefit computations.
Miller-Hooks et al.(30) identified the factors that have the greatest effect on travel delay, fuel consumption, and emissions. For example, roadway geometry (such as number of lanes, gradient and curvature, density of ramps in the roadway segment, traffic volume and composition, and weather) influence the available capacity of a roadway segment and fuel consumption rates.
Initial runs were completed in the earlier work to study trends in travel delay and fuel consumption estimates resulting from univariate changes in the identified factors as well as correlations between factors. Table 6 summarizes the factors that were considered and the ranges of the factors used within these initial experiments. One of the findings was that the percentage of trucks and segment grade are independent with other explanatory variables. This insight was exploited in the creation of the regression models presented herein.
An additional goal of the initial runs made in the earlier research was to assess VISSIM’s capacity to capture the effects of changes in the various identified factors. It was found that capturing the effects of weather, density of ramps, and horizontal curvatures on roadway performance required changes to the free-flow speeds of vehicles travel on the main lanes.
| General Attributes | Factors | Range Used |
|---|---|---|
| Geometry of the roadway segment | Segment length | *20 miles |
| Number of lanes and average lane width | 2–8 lanes, 12 feet | |
| Lateral clearance (shoulder) | 6 feet | |
| Ramps | 0 to 20 ramps/mile | |
| Horizontal curves | Straight, Mild, Sharp | |
| Segment gradient | 0, 2.5, 7.5 percent | |
| Traffic characteristics | Free-flow speeds (FFS) | 55–75 mph |
| Ramp FFS | 25–35 mph | |
| Traffic flow rate | 200–2,200 (vehicles per lane per hour, vplph) | |
| Percentages of trucks in traffic flow | 0–18 percent | |
| Incident attributes | Incident severity | Shoulder-only through up to 1 open lane in the segment |
| Average incident duration | 0–240 minutes (5-minute increments up to 2 hours, 30-minute increments from 2–4 hours) | |
| Rubbernecking effect | 500 feet upstream of incident location | |
| Weather conditions | Clear, Light Rain, Heavy Rain, Snow, Fog, Icy condition, Low Visibility, Wind | |
*Modified for this study to capture longer backup queues.
Replicating Incidents within the VISSIM Platform. Numerous simulation-based traffic studies have used a variety of methods to model traffic incidents (i.e. events involving vehicles that block one or more lanes or the shoulder) within the VISSIM platform. VISSIM does not offer a specific technique for replicating incidents. This study employed the tools offered within the COM interface to model an incident by placing two passenger vehicles, each with a speed of zero, in each blocked lane in the incident location for the incident period. Specifically, the vehicles were placed within the simulation at the incident location (in the blocked lanes) from the start time of the incident to the end of the incident’s clearance time, as shown in figure 2.
Incidents were assumed to arise adjacent to the shoulder. Thus, in an incident involving one blocked lane, that lane was the lane closest to the shoulder. In an incident with two lanes blocked, the two lanes closest to the shoulder were assumed to be involved. Combinations where other lanes, such as the middle lane or the far left lane, were the only lanes blocked were not considered.
At the end of this incident period, vehicles involved in the incident were simultaneously removed from the blocked lanes and vehicles traveling in the affected lanes accelerated until they reached their original desired speed.
Additionally, the incident impact area was assumed to span at most 20 miles and incident duration for incidents involving TIM implementations would not exceed four hours.
To capture the impact of the rubbernecking effect associated with the incident, temporary reduced speed areas in the adjacent lanes were set in the simulation. The inclusion of this effect in the adjacent lanes allows the replication of reduction in speed in unblocked lanes during the incident period and reflects the lower capacity of the highway segment. Hadi et al.(31) found that, within the VISSIM platform for freeways with 3 lanes (in a single direction), a speed of 20 mph in adjacent lanes results in the suggested available capacity for the incident period according to the Highway Capacity Manual 2000.(32) The speed reduction value by lane required to capture the capacity reduction due to rubbernecking in freeway segments with more than four lanes (in a single direction) was determined experimentally in a previous study.(30)
Setting the rubbernecking effect in this manner imposed an additional modeling step. To set up the reduced speed area, the desired speed along that stretch of roadway was reduced to 20 mph. Thus, VISSIM computed the travel delay in this area assuming a desired speed of 20 mph. However, the desired speed needed for travel delay computation (equation 1) is the preincident desired speed. The delay incurred due to the speed reduction associated with the incident should be counted in the travel delay estimates. Consequently, VISSIM 6.0 will underestimate the travel delay due to the incident. To address this, travel delay was recomputed using the preincident desired speed of each vehicle recorded in the vehicle record output file.(12)
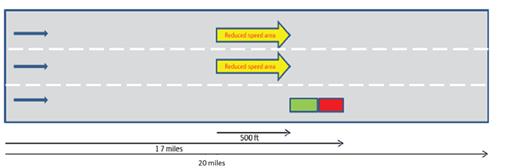
© University of Maryland, College Park. Used with permission.
Figure 2. Diagram. Incident layout on typical three-lane unidirectional freeway segment.(30)(11)
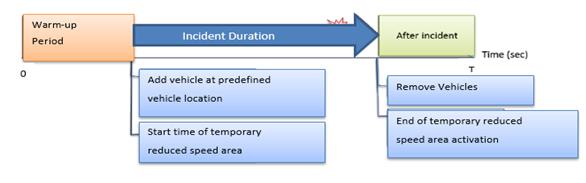
Replicating an Incident in a Simulation Run. Details associated with the replication of a single incident within the simulation environment are described below.
Simulation Time. For incident scenarios with an incident duration of less than 120 minutes, one replication involved 11,100 simulation seconds, which included a 30 minute warmup period, 300 seconds from the end of the warmup period until the incident occurrence, and 2.5 hours of data collection. The simulation time was increased to 18,300 simulation seconds for incidents with an incident duration of 120 to 240 minutes (to include 4.5 hours of data collection).
The choice of the 1,800 second warmup period was made based on a suggestion given in the VISSIM software user manual.(33) The warmup period is required to load the segment and achieve a steady traffic flow along the segment by the start of the analysis period. As noted, incidents were set to occur 300 seconds after the end of the warmup period or 2,100 seconds into the simulation. A detailed analysis to determine the length of the warmup period can be found at Miller-Hooks et al.(34)
The actual time required for each replication was approximately 480 seconds for incident durations under 120 minutes or 900 seconds for incident durations between 120 and 240 minutes on a Dell Precision T7500 personal computer with a 3.20 gigahertz quad core processor and 12 gigabytes of random access memory running a 64-bit Windows 7® operating system.
Random Seeds. The VISSIM user manual (REF) (PTV AG 2014) suggests conducting a minimum of three runs with different random seeds for each simulation experiment and reporting the average performance values over these runs in the final results. Additional experiments revealed that only small improvements in computational accuracy could be achieved using a higher number of random seeds.(34)(12)
Simulation Resolution. VISSIM is a time-based (as opposed to event-based) simulation technique. Thus, a time step for updating the vehicle locations must be set. The software user manual (REF) (PTV AG 2014) suggests a simulation resolution of one time step per simulation second. In initial experiments, it was found that using one time step per second led to high values of lost vehicles (vehicles that cannot enter the network). Thus, five time steps per simulation second (or 0.2 time steps per simulation second) were used instead.(12)(30)
Traffic Flow Calibration. Calibration of the simulation software to actual traffic conditions is essential to ensure that the simulation model will adequately replicate reality. Miller-Hooks et al.(12) identified five car-following and lane-changing parameters in VISSIM that had significant effects on travel delay estimation. After completing an extensive effort to calibrate a model of a 41-mile Maryland freeway (82 miles in both directions) against actual travel time measurements, the research findings suggested changes to four of the five values. The parameter settings suggested to be calibrated are: “Following” Variation (CC2), “Following” Thresholds (CC4&5), Safety Distance Reduced Factor (SDRF), and Look Back Distance (LBD). Their definitions, default values, possible range in VISSIM, and the final set that are used in this study are listed in table 7. SDRF and LBD are lane-changing parameters associated with driver behavior. These settings are discussed in more detail by in Miller-Hooks et al.(12)
The recommended parameter settings were based on a comparison between actual measured travel times and estimates of travel times obtained using VISSIM 5.4 for a studied roadway. Additional experiments were conducted herein to assess the use of these parameters within VISSIM 6.0. Runs were made with both VISSIM 5.4 and 6.0, and no significant changes in estimated travel delay were observed in results from runs involving the study segment. Thus, these recommended parameters were used in this study.
| Parameter | Definition | Default Value | Adjusted for SSP-BC Tool |
|---|---|---|---|
| “Following” Variation (CC2) | Following variation: desired safety following distance | 4 meters | 39.37 feet |
| “Following” Thresholds (CC4&5) | Lower and upper following threshold | 0.35 mph | 0.1 mph |
| Safety Distance Reduced Factor (SDRF) | Safety distance reduced factor: effects safety distance during lane changing | 0.6 | 0.1 |
| Look Back Distance (LBD) | Look back distance: defines the distance at which vehicles will begin to attempt to change lanes | 200 meters | 3,280.83 feet |
SSP-BC = Safety Service Patrol Benefit-Cost
Ideally, all possible combinations of number of lanes in the roadway segment, roadway grade, FFS, traffic volume and composition, number of lanes blocked, and incident duration with ranges presented in table 8 would be replicated. This would require the replication of 246,960 combinations, each repeated three times to accommodate three seeds. Thus, 740,880 runs would be needed. At 700 seconds per run on average, using the computer described previously, it would take approximately 16 years to run these simulation combinations. This estimate does not account for the time required to process the output.
Through the development of regression models and the use of the hybrid statistical-simulation methodology, the number of simulation runs can be reduced significantly with little reduction in accuracy. To achieve this, two sets of runs were completed. The first involved a random sample of 1,319 incidents. To attain a representative sample, statistical distributions of incidents were studied in the literature and all the factors were selected in accordance with identified distributions. Incident frequency distributions were used to calculate the probability of each incident category by severity. For example, vehicle breakdowns were assigned higher occurrence probabilities than were rarer events such as a four-lane blockage incident on a six-lane highway. It was assumed that the explanatory variables are independent and uncorrelated with one another. Where this assumption was invalid, appropriate modeling techniques were used to minimize any effect on the development of the regression models.(30) Results from this first set of simulation runs were used to develop and calibrate the regression models. These models are discussed in more detail below.
| Factor | Range used |
|---|---|
| Number of lanes and average lane width | 2–6 lanes, using increment of one lane |
| Segment gradient (percent) | 0, 2.5, 7.5 percent |
| FFS (miles per hour, mph) | 40–75, using 10-mph increment |
| Traffic flow rate (vehicles per lane per hour, vplph) | 500, 1,000–2,200, using 200 vplph increment |
| Percentage of trucks in traffic flow (percent) | 0–18 percent, using 2-percent increments |
| Incident severity | Shoulder, up to only 1 open lane in the segment |
| Average incident duration | 0–240 minutes (5-minute increment up to 120 minutes, 30-minute increments from 120–240 minutes) |
The second set of runs involved replication of 162,599 incidents, including the 1,319 incident scenarios from the first set of runs. These runs were required as input to the hybrid statistical-simulation methodology introduced by Miller-Hooks et al.(11) and used herein. This approach was developed to improve the estimation accuracy of these regression models.
Regression equations were developed for estimating travel delay for light-duty vehicles (passenger cars), travel delay of heavy-duty vehicles (including trucks), and fuel consumption for passenger cars. Fuel consumption savings for heavy-duty vehicles are incorporated through the monetization of related travel delay savings and thus need not be treated separately. These regression equations, the methods undertaken for their calibration, and the results from statistical analyses to test their goodness-of-fit are presented in this section.
The linear regression models of travel delay and fuel consumption were obtained based on the explanatory variables included in table 8. Additional variables based on the same factors were developed through composition of variables techniques in which the variables were taken to different powers or were multiplied. Different linear and nonlinear regression models were tested and assessed using various goodness-of-fit tests. For each model, a stepwise technique was employed to find the best subset of explanatory variables to include in these models. The SAS statistical software package was employed for the statistical analysis conducted herein.
To choose the best estimation model for travel delay and fuel consumption from the set of candidate models, the coefficient of determination (R-square), adjusted R-square, graph of residuals, maximum log likelihood (assuming normality of the model error term), and analysis of variance and nonlinearity were studied. The maximum log likelihood estimate was used to compute the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). All of these factors were considered in choosing the best-fitting model for each performance metric (travel delay and fuel consumption), resulting in the final three equations. An example of the regression model development process is shown in appendix A.
Selected Regression Models. The final regression models for travel delay for light-duty vehicles (LDV) and heavy-duty vehicles (HDV) and fuel consumption of light-duty vehicles are presented. The nomenclature used in these models is given subsequently.
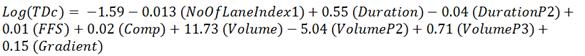
Figure 3. Equation. Final Model of Travel Delay of Light-Duty Vehicles (Cars)
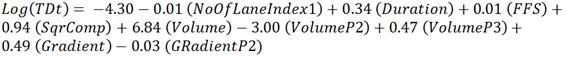
Figure 4. Equation. Final Model of Travel Delay of Heavy-Duty Vehicles (Trucks)
where
| TDc = | Total travel delay of cars (hours) |
| TDt = | Total travel delay of trucks (hours) |
| LogTDc = | Ln(TDc) |
| LnTDt = | Ln(TDt) |
| NofLaneIndex1 = | (Number of open lanes / Number of lanes in each direction)*100 |
| Duration = | Incident duration (hours) |
| DurationP2 = | Incident duration2 (hour2) |
| FFS = | Free-flow speed (km/h) |
| Comp(*10k) = | Traffic composition – percentage of trucks |
| SqrComp = | Percentage of trucks power 0.5 |
| Volume = | Traffic volume (vplph, 1,000) |
| VolumeP2: | Traffic volume power 2 (vplph2, 1,0002) |
| VolumeP3 | Traffic volume power 3 (vplph3, 1,0003) |
| Gradient | Roadway gradient |
| GradientP2: | Roadway gradient power 2 (percent2) |
While the final regression model for fuel consumption of cars has an acceptable R-square value at 0.812, the model does not fully meet assumptions made for the residuals–constant variance.
The regression-simulation hybrid approach introduced by Miller-Hooks et al.(12) was employed to further improve this model as described in the following.
Fuel Consumption Estimation. Miller-Hooks et al.(12) introduced and tested a hybrid statistical-simulation modeling approach in which the performance measures obtained from simulated incidents were integrated with estimates obtained from developed regression models. The aim of the technique is to reduce the error of the estimation models and more accurately capture the relationship between the performance measure and explanatory variable values. To employ this hybrid statistical-simulation approach, the total fuel consumption of cars was computed by summing two independent components: (a) and (b). Component (a) is the fuel consumption under an identical incident but with zero percentage of trucks (Truck %) and zero roadway gradient (Gradient). This baseline incident scenario is simulated in VISSIM to obtain fuel consumption as described above. Component (b) is the additional fuel consumption due to a higher percentage of trucks or different roadway gradient of the actual incident, compared with the baseline incident scenario. This excess consumed fuel is estimated by taking advantage of the independence of regression variables. Independence of variables allows estimation of the relevant proportion of fuel consumption associated to Truck % and Gradient using the lookup data generated based on microscopic simulation data. This is illustrated in figure 5.
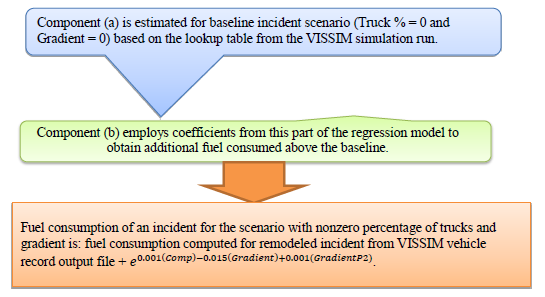
© University of Maryland, College Park. Used with permission.
Figure 5. Diagram. Statistical-simulation hybrid approach for estimating fuel consumption of light-duty vehicles.
Emission Calculation. Similarly to approaches used in Miller-Hooks et al.,(12) fuel consumption and emission computations are adopted from Melanta et al.(36) Fuel-based emission factors (i.e., mass of pollutant produced per unit of vehicle activity) The emission factor for pollutant (EFPol) for the LDV and light-duty trucks (LDT) vehicle categories for major fuel types (i.e., gasoline and diesel) were obtained from the U.S. Environmental Protection Agency (refer to table 9). These emission factors in combination with other variables specific to the vehicle categories (e.g. fuel economy, time spent on roads, etc.) and fuel (i.e., density, EFPol) were then used to calculate the emissions output for each pollutant (EMPol) using the equation in figure 4.
![]()
Figure 6. Equation. Emission Estimation for Co2, HC, CO, NOx.
The sulfur content in a fuel affects the amount of SOx emissions produced when fuel is consumed. Therefore, the sulfur contents (SCFuel as obtained from table 10) for gasoline and diesel were used to estimate the SOx emissions for a vehicle category using the following relationship:
![]()
Figure 7. Equation. Estimation of SOX emissions.
where
| EMPol = | Emission for pollutant (g) |
| EMSOX = | SOx Emission (g) |
| EFPol = | Emission factor for pollutant (g/mile) |
| ρFuel = | Density of fuel (g/gal) |
| Fuel Economy LDV/LDT = | Fuel Economy for vehicle category (gal/mile) |
| T = | Total time travelled by vehicle category (sec) |
| SCFuel = | Sulfur Content of Fuel (ppm) |
| FR = | Fuel consumption rate (g of fuel/sec) |
While the equations in figures 4 and 5 use the term FR* T to calculate fuel consumption, in our tool, the fuel consumption values are calculated from the previous step and those values are used to replace FR* T in each of the equations.
| Vehicle | Fuel Economy (mile/gal)1 | Emission Factors for Gasoline (g/mi) | |||
|---|---|---|---|---|---|
| HC | CO | NOx | CO2 | ||
| LDV | 22.1 | 2.8 | 20.9 | 1.39 | 451 |
| LDT | 17.6 | 3.51 | 27.7 | 1.81 | 637 |
CO = carbon monoxide, CO2 = carbon dioxide, HC = hydrocarbon, NOx = nitrogen oxide.
| Fuel | Base Fuel | ρ(g/gal) | SCFuel (ppm) |
|---|---|---|---|
| Gasoline | Base fuel | 2834.95 | 80 |
| Diesel | Base fuel | 3210.98 | 500 |
Secondary Incidents Calculation. A robust approach for calculating secondary incidents is explained in Chou and Miller-Hooks.(10) However, data requirements and analysis required for the method is beyond the capability of many TIM programs. Therefore, the secondary estimation method developed by Miller-Hooks et al.(11) is adopted. The number of secondary incidents without TIM is assumed to be linearly correlated to the travel delay ratio of without and with implementation of TIM, as shown in the equation in figure 8.
![]()
Figure 8. Equation. Secondary Incident Estimation.
where
Nwo = Number of secondary incidents for extended incident duration case (without case).
Nw = Number of secondary incidents in base case (with case).
TDwo = Travel delay for the extended case.
TDw = Travel delay for the base case.
The number of secondary incidents Nw as a fraction of primary incidents is given as user input. For this analysis, the number of secondary incidents ( Nw ) as a fraction of primary incidents must be known regardless of the chosen secondary incident classification method. TDwo and TDw are parameters.
Monetary Values. To isolate a single unit for evaluation of a TIP strategy, congestion-related travel delay (vehicle-hours), fuel consumption (gallons), and number of secondary incidents prevented are converted into their monetary equivalents. Sources of the monetary equivalents in the TIM-BC tool proposed herein are provided in table 11. Four individual tables containing this information support the BC ratio computation within the tool. They are also designed to be updatable.
| Variable | Corresponding Output | Description | Source |
|---|---|---|---|
| Average gasoline prices | Gallons of fuel saved | Used to monetize the wasted fuel that would result from increased congestion if SSP did not exist. NOTE: fuel is already factored into the Hourly Truck Cost, and the monetization of wasted fuel should only be performed on the passenger vehicle share.(37) | U.S. Energy Information Administration, Gasoline and Diesel Fuel Update; updated 5:00 p.m. every Monday; http://www.eia.doe.gov/oog/info/gdu/gasdiesel.asp |
| Average labor costs | Hours of delay prevented | Used to monetize lost productivity of passenger vehicles resulting from increased congestion if SSP did not exist.(38) | U.S. Department of Labor, Bureau of Labor Statistics; State Occupational Employment and Wage Estimates; http://www.bls.gov/oes/current/oessrcst.htm |
| Commercial vehicle costs per hour | Hours of delay prevented; Gallons of fuel saved | Used to monetize lost productivity of commercial vehicles resulting from increased congestion if SSP did not exist.(39) | ATRI, An Analysis of the Operational Costs of Trucking: A 2014 Update, http://www.atri-online.org/wp-content/uploads/2014/09/ATRI-Operational-Costs-of-Trucking-2014-FINAL.pdf Based on actual operational cost data collected from motor carriers across the country, representing a cross-section of industry sectors. |
| Secondary incident cost | Number of secondary incidents averted | Represents only the cost of property damage. Used to monetize the cost of additional secondary incidents that would result from increased congestion if SSP did not exist.(40) | National Highway Transportation Safety Administration, The Economic Impact of Motor Vehicle Crashes: 2000 (Revised). |
While some previously developed BC ratio estimates made for TIM strategies have included monetized emissions equivalents in the savings computation, a review of the literature indicates that the available monetary equivalents are based largely on soft, intangible costs as opposed to more quantifiable costs, such as the price of a gallon of fuel. Thus, the value for tons of emissions saved is reported separately and is not included in the BC ratio computed in the TIM-BC tool.(11)
Average hourly wages are used to convert savings in travel delay to a monetary equivalent. Wage values are available both at metropolitan levels and as a State average. Additionally, data containing the share of commercial vehicle miles traveled (VMT) compared to total VMT by State were used for the truck composition estimates for each State. These data are necessary to distinguish between the benefits derived from savings in travel delay for passenger vehicles and those for commercial vehicles. The average operational cost of trucking for 2014 is $67 per hour based on table 11.
The BC ratio is highly sensitive to the cost of secondary incidents. In this study, cost represents “property only damage” incidents and for 2014 that value is assumed to be $4,736 based on table 11. Other costs associated with higher severity incidents and congestion due to secondary incidents were not considered.
Computing Total Benefit. To compute the total savings in travel delay, fuel consumption, emissions, and secondary incidents resulting from a TIM strategy in a segment over a period of time, information pertaining to the incidents arising along the studied roadway segment during the study period is needed. Specifically, the distribution of incidents with respect to lane blockage must be known (or approximated). Assuming any two incidents are independent, TSj, the total savings of type j, where j= {total travel delay, fuel consumption, emission, secondary incidents} for every incident i arising during a period of time over a road segment as described in the equation in figure 7 can be computed. When using this method, it is necessary to assume that an individual incident has no influence on other incidents on the road.
Furthermore, savings in travel delay and fuel consumption is related to geometry characteristics of the study segment and weather conditions at the time of the incident by adjusting FFS. The geometry characteristics are similar for all incidents in a study segment. However, the weather condition might vary incident by incident in a period of time. One incident under weather conditions would have a different actual speed. Therefore, having the probability of each weather type, Pk, the savings from one incident can be estimated as exhibited in the equation in figure 9.(11)
![]()
Figure 9. Equation. Total Savings Estimate.
where
TSj = Total saving of type j.
j = Type of saving {Total travel delay, fuel consumption, emission pollutants}.
i = Individual incidents.
k = Weather conditions {Clear, light rain, heavy rain, low visibility, snow, fog, icy}.
Pk = The probability of weather condition.
Sjik = Saving type j in incident i of weather condition k.
Given monetary conversion rates for travel delay, fuel consumption, and secondary incidents, total program benefit can be computed. Assuming that benefits are uniformly distributed over length, the total benefit of the TIM strategy over the study period and roadway segment can be computed as shown in the equation in figure 10.
![]()
Figure 10. Equation. Estimation of total benefits of implementing a TIM strategy.
where
B = Total benefit of implementing a TIM strategy.
j = Travel delay (1), Fuel consumption (2), Emissions (3), and Secondary incidents (4).
MEj= Monetary equivalent of saving j.
L = Length of study segment.
The approaches to estimating benefits of various TIM programs are made consistent by using the D/P-E method. However, the estimation of the number of incidents and incident durations are different for different TIM strategies. More details about this estimation are provided in appendix B.
The total cost of a TIM strategy, TAC, has two major components: operating cost and other related costs. For SSP, the operating cost is a function of the number of roving SSP trucks along the study segment, hourly operating cost per truck, number of working hours, number of workdays in a year, fuel costs for each vehicle, cost of giveaway fuel to drivers whose vehicles ran out of gas, and other costs, such as vehicle maintenance. The equation in figure 11 shows the method to calculate the total cost of a TIM strategy.
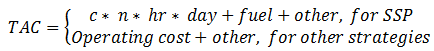
Figure 11. Equation. Method for calculating the total cost of a TIM strategy.
where
TAC = Total annual cost for operating a TIM strategy in dollars.
c = Cost per truck-hour {hourly wage of driver, fuel cost of the vehicle}.
n = Number of roving trucks.
hr = Number of working hours in each day.
day = Number of workdays in a year.
fuel = Annual giveaway fuel consumption.
other = Other related cost.
Operating Cost = The operation cost for a TIM strategy in dollars.
The cost of many TIM strategies can oftentimes be easily calculated, as many TIM programs are outsourced and the charges are provided contractually. The cost of a TIM strategy for a specific roadway segment may be less clear. Two general methodologies were considered herein for the computation of segment-based costs. First, given total program costs, costs associated with a given segment can be computed based on the proportion: number of the total incidents to which the TIM strategy implemented for the study segment to total incidents that implemented the TIM strategy. This computation is captured in the equation in figure 12.
![]()
Figure 12. Equation. Method for calculating costs of operating TIM strategiesalong a corridor.
where
Cn = Cost of operating a TIM strategy along the study segment n
TAC = Total annual cost of the TIM strategy
Nn = Number of incidents implemented during the TIM strategy along the study segment n
Ntot = Total number of incidents implemented during the TIM strategy
The second portion of the methodology is to compute the costs associated with a given segment by the proportion of its length to the total length of covered roads that apply a TIM strategy. Using this method, we assume that cost is uniformly distributed over the length of the roads of the TIM strategy service area. The first method is used in developing the TIM-BC tool in this study.
The obtained benefit from equation 8 and cost from equation 10 are used to assess the segment-based BC ratio for a given TIM strategy over the study period. The TIM-BC tool provides multisegment analysis. The BC ratio of n segments is computed from the ratio of the sum of benefits to the sum of costs for all segments, as shown in the equation in figure 13.
![]()
Figure 13. Equation. Model for calculating benefit cost ratios.
where
B/Ctot = B/C ratio of multiple segments.
Bn = Obtained benefits of implementing a TIM strategy for the segment n
Cn = Costs of implementing a TIM strategy for the segment n
Note that within the TIM-BC tool, savings in pollutant emissions are not translated to dollars. Thus, it is not included in the BC ratio. Emissions reductions are given separately in the form of metric tons.
Additional savings that have not been quantified in this study include improved safety not only in preventing secondary incidents, but also in improving the users’ feeling of security on transportation systems, reduced congestion costs associated with the secondary incidents, more efficient freight transit system, greater environmental benefits, and the accrual of advantages to other agencies, such as additional time available for troopers for more urgent tasks that TIM strategies cannot address. The following is a list of some additional costs associated with incidents:
Numerous additional sources of benefits in cost reduction have not been included in the computation of program benefits within the proposed TIM-BC tool. The exclusion of the many additional benefits within the TIM-BC tool results in conservative BC estimates.